双碳背景下发达地区工业发展与电力消费关系研究
——以上海市为例
2022-11-03李舒婕
李舒婕
(上海电力大学, 上海 200090)
1 研究意义
由图1 可知,中国电力消费量逐年上升,其中工业电力消费量占总电力消费量的很大比重,远高于其它产业,可见我国在工业生产上对于电力的需求量仍然十分巨大。对比上海市历年总电力消费量与工业电力消费量的关系(见图2),可以看出,由于上海市城市化进程较快,虽然其第二产业电力消费量占总电力消费量的比重历年减小,但是也保持在45%以上的水平,远超其它产业。
本文选取经济发展较为发达的上海市作为研究地区,研究其电力工业的发展情况。故选取上海市电力消费量和工业生产总值两者之间的关系进行研究,利用协整理论和误差修正模型来分析两者之间的长期均衡关系与短期动态调整,利用Granger 因果检验分析其关系,并对模型进行回归分析,进而预测未来的电力需求情况,提出相关政策建议。
2 计量OLS 回归模型
本文目标为研究上海市电力消费量和工业生产总值之间的关系,使用Eviews10 软件分析数据。在进行协整分析之前,为避免伪回归,首先检验时间序列的平稳性,使用ADF 检验来验证其是否为同阶单整。在同阶差分的基础上,使用E-G 两步法检验两个变量之间是否具有长期稳定的均衡关系。并使用误差修正模型估计两个变量之间的短期关系,使分析更加全面。利用Granger 因果检验对其进行因果关系检验,分析其经济意义。最后对其进行回归,分析其回归系数的经济意义[1-3]。
3 实证分析
3.1 数据来源与处理
为研究上海市第二产业的经济增长对上海市电力消费量的影响,于上海市统计局选取上海市自2000—2019 年的相关数据。以上海市工业生产总值(记为GDP)反映上海市第二产业的经济情况,与上海市电力消费量(E)构建回归模型。两者趋势图如图3所示。
由图3 可得,两者呈现出线性相关关系,故假设二者之间关系设定为一元线性回归模型:
式中:μi为随机误差项,即除上海市工业生产总值,影响上海市电力消费量的其他因素。假设该模型满足古典假设,本文利用计量经济学软件eviews 进行分析。本文数据全部来自于上海市统计局。
3.2 序列的平稳性检验
在进行协整分析之前,为避免伪回归,需要检验时间序列的平稳性。本文采用ADF 检验法检验时间序列的平稳性。eviews 输出结果如表1 所示。
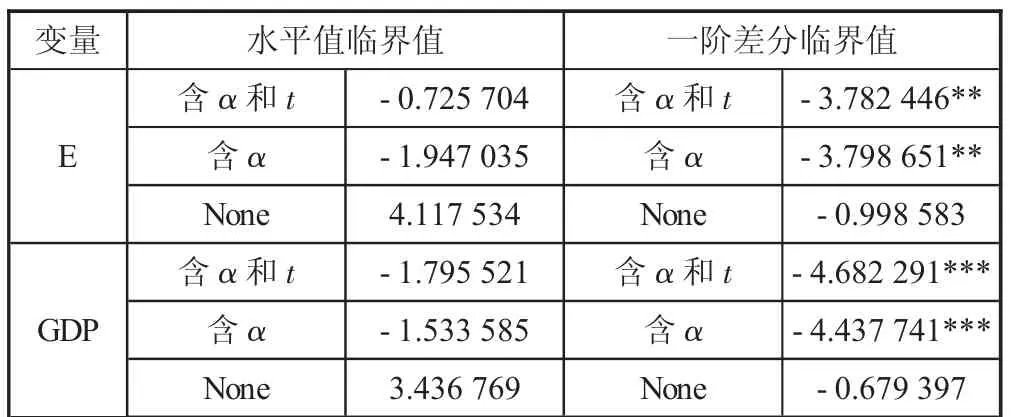
表1 平稳性检验
两个变量的原序列的无论是在含有截距项和时间趋势项时,还是仅考虑常数项的情况时,均为一阶单整序列,可以进一步验证两者之间的协整关系。
3.3 序列的协整检验
协整关系可以表明,变量之间存在的长期均衡变动关系,根据协整理论,两个非平稳变量之问的某种线性关系可能是平稳的,表现为其残差是平稳序列。
本文选取的两个变量GDP 与E 都为一阶单整,满足协整的前提条件。使用E-G 两步法进行检验,只有当回归方程的残差为平稳变量,并且变量之间存在协整关系时,线性回归才是真实的。残差R 的平稳性检验eviews 输出结果如表2 所示。
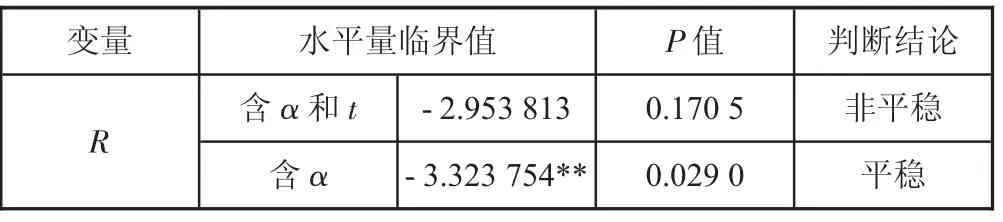
表2 E-G 两步法残差平稳性检验结果
表2 中残差序列在水平含有常数项的模型中,拒绝了5%置信区间的原假说,表示残差R 序列为平稳序列,变量GDP 与E 变量之间存在协整关系,它们之间具有长期稳定性。
3.4 格兰杰因果检验
本文在研究分析GDP 与E 之间的因果关系时,采用Granger 检验法分析两者的因果关系与方向。EVIEWS 输出结果如表3 所示。
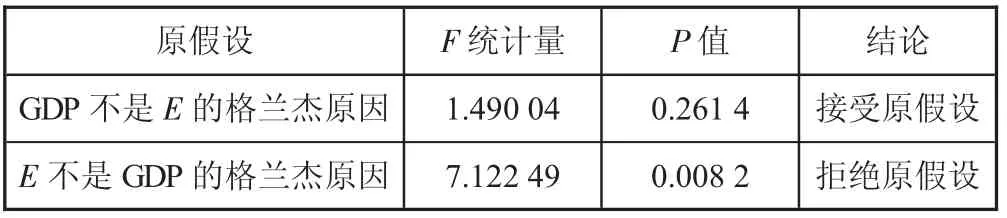
表3 格兰杰因果检验
结果表明,E 是GDP 的格兰杰原因,说明电力消费是工业产业经济快速发展的原因。在我国经济社会的快速发展过程中,工业的电力消费一直处于高位,电力作为基础设施,其消费对于工业生产总值的提高具有重要贡献。
3.5 误差修正模型
协整检验中验证了上海市工业生产总值(GDP)与上海市电力消费量(E)的序列成(1,1)阶协整关系,现建立其误差修正模型。以E 关于GDP 的协整回归中的平稳残差序列et作为误差修正项,可建立如下误差修正模型:
式中:et-1的参数估计值为负,表明了前一期对后一期的修正。由协整模型得到E 关于GDP 的长期弹性为0.131 7,由误差修正模型得到E 关于GDP 的短期弹性为0.079 7。
3.6 OLS 回归分析
利用eviews 软件进行一元线性回归分析,得出模型:
评价模型:模型估计结果说明,在假定其他变量不变的情况下,上海市工业生产总值每增加1 亿元,上海市电力消费量就会增加0.131 7 亿kWh;从回归估计的结果看,模型拟合较好。可决系数R2=0.985 8,表明上海市电力消费量变化的98.58%可由上海市工业生产总值的变化来解释。
序列相关检验:由回归结果可知,在5%显著性水平下,n=20,k=2,查表得dL=1.20,dU=1.41,D.W.=1.1665<dL,故判断模型随机项存在正自相关。由残差图(图3)可知,残差的变动有系统模式,连续为正和连续为负,表明残差项存在一阶正自相关,模型中的t 统计量和F统计量结论不可信,需采取补救措施。
3.7 采用广义差分法估计模型
利用eviews 软件,对残差序列进行滞后一阶的自回归,可得回归方程:
由此可知p^=0.350 2,对原模型进行广义差分,得广义差分方程:
模型的一阶广义差分的估计结果为:
在5%显著性水平下,n=19,k=2,查表得dL=1.18,dU=1.40,D.W.=1.845 4>dU,表明经广义差分法变换后的模型已经不存在序列相关性。对比原模型与广义差分后的模型,可知普通最小二乘法低估了GDP 前的回归系数的标准误差。β0=254.697 9/1-0.350 2=391.963 5,由此,得到最终的回归模型:
模型估计结果说明,在假定其他影响因素不变的情况下,上海市工业生产总值每增加1 亿元,上海市电力消费量就会增加0.125 6 亿kWh。
4 结论与建议
由实证分析可得上海市工业生产总值与电力消费量之间具有长期稳定的均衡关系,由协整模型得到电力消费量关于工业生产总值的长期弹性为0.131 7,由误差修正模型得到电力消费量关于工业生产总值的短期弹性为0.079 7。在假定其他影响因素不变的情况下,上海市工业生产总值每增加1 亿元,上海市电力消费量就会增加0.125 6 亿kWh。
