基于灰色-加权马尔可夫预测模型的西安常住人口预测

王朱宇，徐小玲，胡哲，叶飞，王亚芳

（延安大学西安创新学院，陕西 西安 710100）

0 引言

在未来，城市的发展跟人口休戚相关。如何吸引外来人口流入并最终留住人才，对一个城市而言就变得更为重要。近年来，政府加大了保障房建设力度，同时社会的商品房供给量年年增加，但到底是供应多少最为合适呢？这个问题值得深入思考。对该问题分析发现常住人口数量是决定供房量的关键因素。以西安常住人口为例，2021年西安市常住人口数据出炉，西安市常住人口持续增长，超过1 300 万。那么对于住房供给力度多大更为合适呢？在这样的背景下，就需要对西安未来常住人口数量进行预测，以便更好规划住房供给。

常住人口数量对住房、教育和就业岗位等多方面都有较深的影响，因此在这些方面展开了诸多讨论，如吕敏怡等人对上海市人口结构变化对住房需求的影响进行了探究，并表明人口年龄结构、家庭规模和结构、人口流动等因素与住房需求的联系最密切。黄甫玥等人从城市外来常住人口对城市就业岗位的依附关系入手，提出了基于就业岗位的城市外来常住人口的预测方法，并对南京未来城市外来常住人口进行了预测。常见的预测方法有一元线性回归法、平滑法、GM（1，1）模型预测法等，如张梦汝等人利用灰色理论的GM（1，1）预测模型对上海市未来十年外来常住人口发展趋势进行预测。灰色预测模型在常住人口预测中的是普遍适用的，但是常住人口数量受多种复杂因素影响，具有较大的随机波动性，需要对该模型进行改进。柴小媚基于灰色模型和回归分析的北京市常住人口预测；高红提出基于灰色神经网络模型的江苏省人口预测；何芳等人利用灰色模型和马尔可夫（Morkov）转移概率的组合法对大城市外来常住人口的居住需求规模进行预测。由于马尔可夫预测可以根据状态之间的转移概率来推测未来发展变化，适用于随机波动较大的动态过程。本文结合两者的优点基于灰色-加权马尔可夫预测模型并对2022—2026年西安市常住人口数量进行预测。

1 GM（1，1）模型预测及结果分析

设原始时间序列=（（1），（2），…，（）对其做一次累加生成运算，即令：

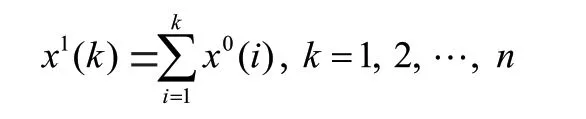
从而得到新的生成数列=（（1），（2），…，（）)，新的数列一般近似的服从指数规律，因此它满足灰色预测的微分方程G(1，1)，其白化形式为：

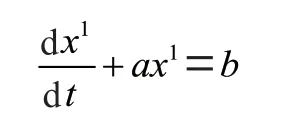
求解微分方程得：

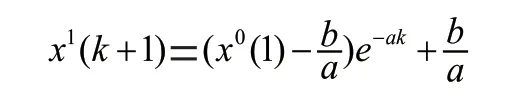
从而得到原始数据得灰色预测值：

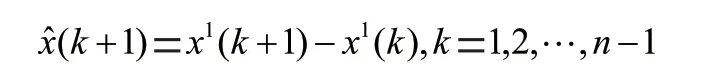
根据上述原理，以2010—2021年共计12年西安常住人口实际统计数据（如图1所示），利用G(1，1)模型对该数据进行预测，并对其结果进行比较分析，结果如表1所示。

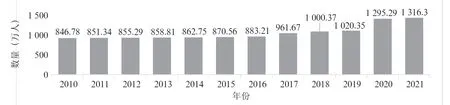
图1 2010—2021年西安常住人口数量统计图（数据来源：西安市统计局）

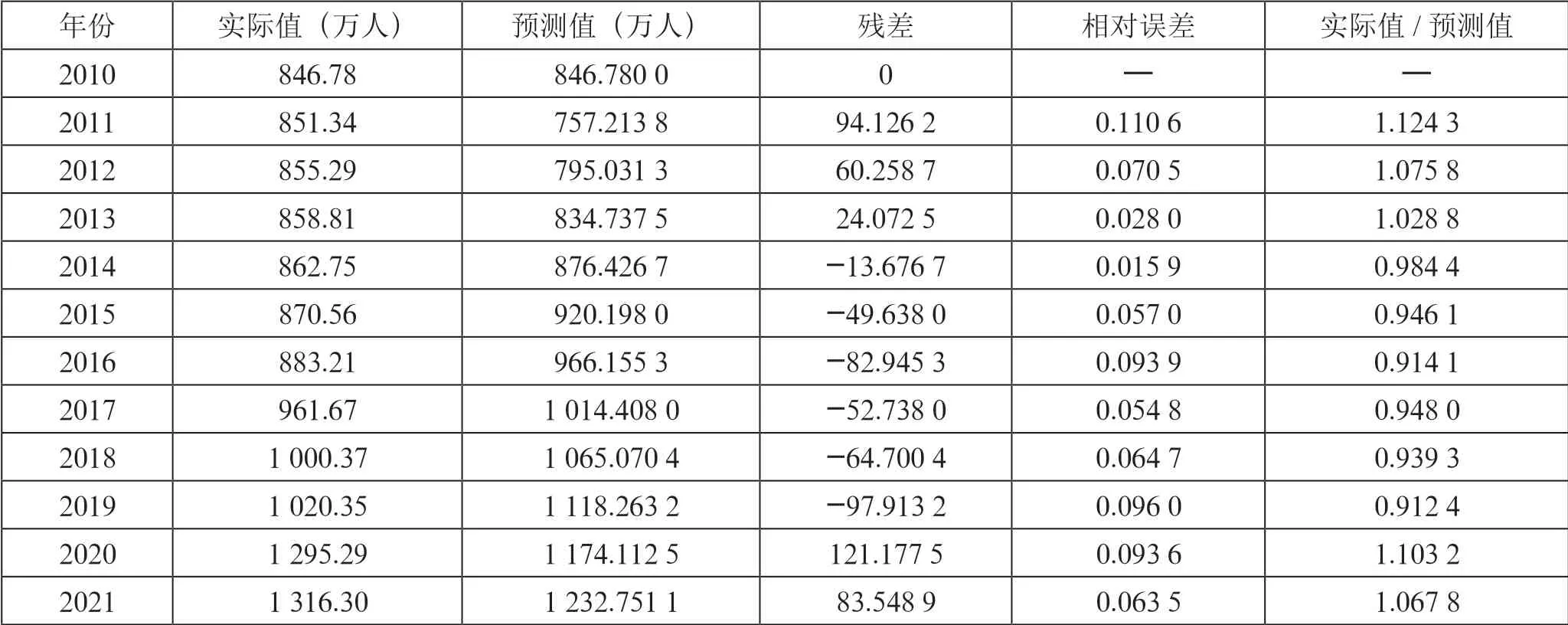
表1 G(1，1)模型预测值（万人）

对模型进行后验差检验和关联度检验，首先计算后验差比值：

根据表2，和值显示预测结果达到了合格水平，这个精度还不够，而小于0.6，表明模型输出结果不满意，并且从图2 也可以看出，西安常住人口是从17年开始大幅增加，这和2017年西安加快人才引进落户政策和二胎政策开放的出台相互印证。但是对未来进行预测时，西安市人口数量预测G(1，1)模拟曲线是一条指数曲线，并且其变化趋势呈现非平稳随机过程的特点。因此基于马尔可夫链具有的“无后效性”特点，在G(1，1)模型的基础上结合马尔可夫链来改进该模型。

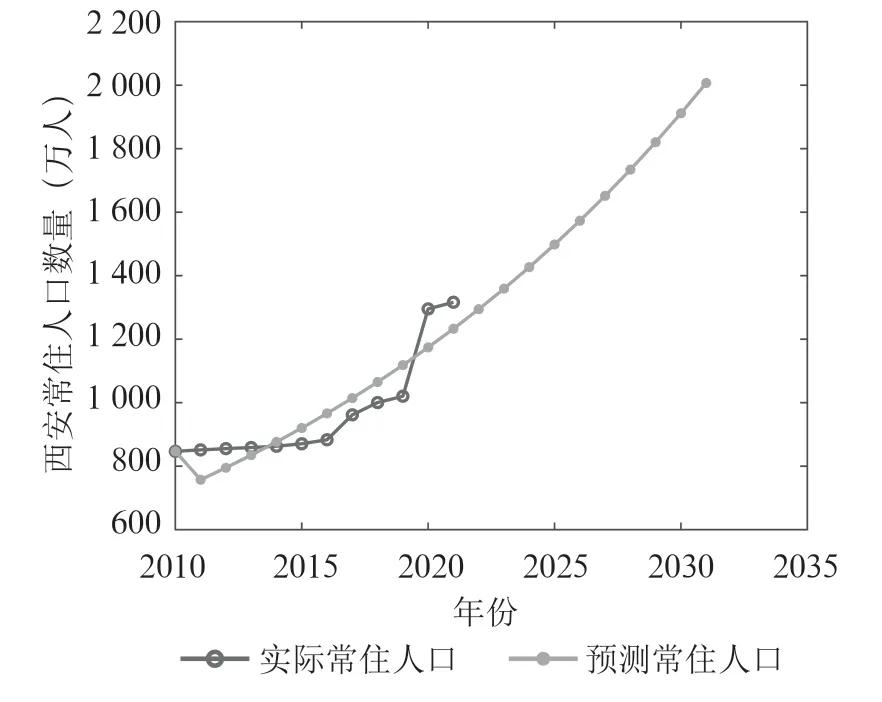
图2 西安常住人口增长曲线

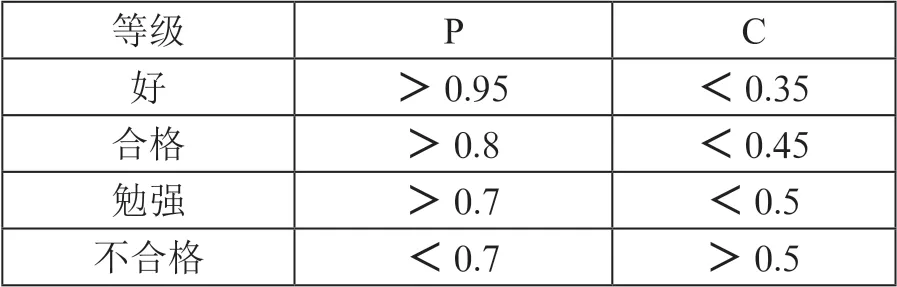
表2 预测精度等级

2 基于灰色-加权马尔可夫模型的常住人口预测

2.1 模型预测

以2010—2021年西安市常住人口总数为依据，在对G(1，1) 进行了分析的基础上，引入加权马尔可夫预测方法对第2 节中的预测结果进行修正，具体步骤为：

步骤1：根据表1 中西安常住人口实际统计值与G(1，1)模型预测值的比值情况，将2010—2021年的数据划分为5 个状态：={0.90 ≤比值＜0.95}，={0.95 ≤比值＜1.00}，={1.00 ≤比值＜1.05}，={1.05 ≤比值＜1.10}，={1.10 ≤比值＜1.15}。那么每年的状态表如表3所示。

表3 状态划分

步骤2：基于各阶自相关系数计算马尔可夫链的权重。设（k），（=1，2，…，）表示西安常住人口数序列，计算序列各阶自相关数的公式为：

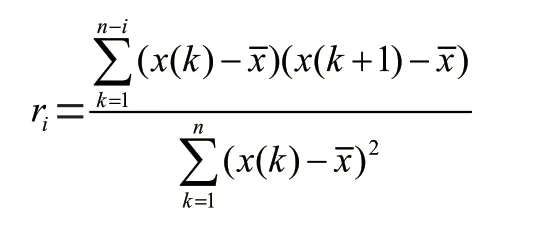
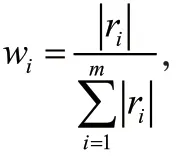
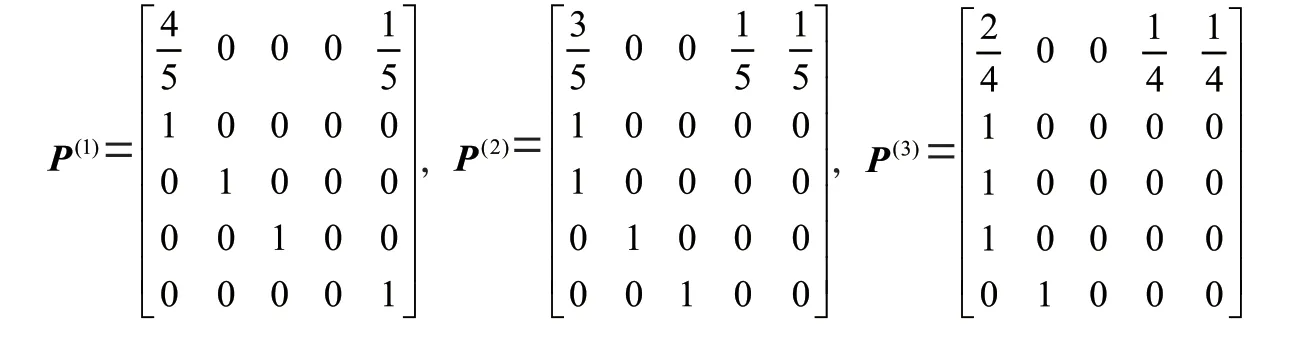
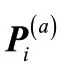
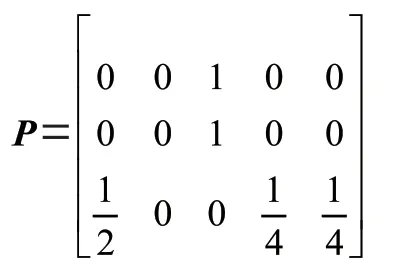
将同一状态的各预测概率加权求和，得到处于该状态的预测概率P：

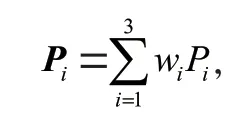
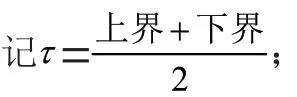
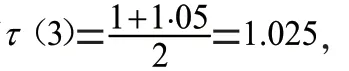
表4 2022年西安市常住人口数量状态预测

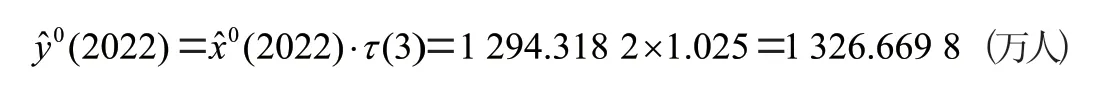
2.2 模型检验

基于灰色-加权马尔可夫预测模型与灰色G(1，1)模型对2010—2021年的西安常住人口数进行拟合和预测，结果对比如表5 和图3所示。

表5 两种方法模拟结果比较

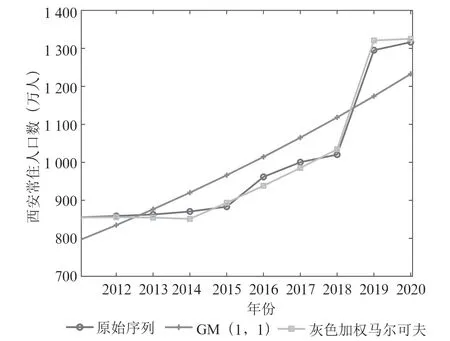
图3 两种方法预测结果比较

对表5 中数据分析，从相对误差的绝对值可以看出，灰色G（1，1）模型均远远高于灰色-加权马尔可夫预测模型；前者的残差范围为[-97.913 2，121.177 5]，后者的残差范围为[-25.586 6，23.342 6]；前者的平均相对误差为6.377 7%，后者为1.278 7%；由此说明后者的拟合精度更高，相较于灰色G（1，1）模型，灰色-加权马尔可夫预测模型预测精度提高了79.95%。同时，图3 表现出灰色-加权马尔可夫预测模型能更好地拟合，并且对西安常住人口预测的效果明显且具有更加理想的预测精度。最后，再进一步基于灰色-加权马尔可夫预测模型对2022—2026年的西安常住人口数量进行预测，其结果如表6所示。综合分析这五年的人口变化情况，发现期间存在常住人口减少情况，但总的变化趋势是增长型的，其平均增长率为2.367 9%。

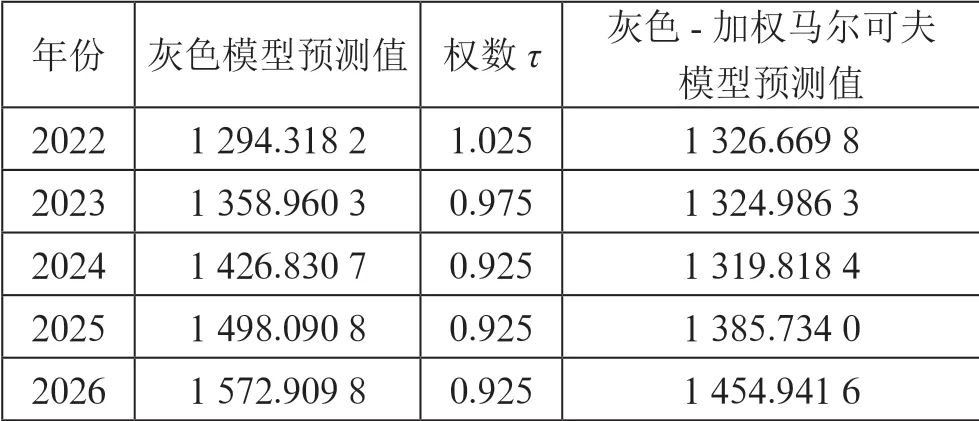
表6 2022—2026年西安常住人口预测结果

3 结论

在西安常住人口数量预测中，针对灰色G（1，1）模型受数据的随机波动性影响较大，预测精度不高这一缺点，本文提出了基于灰色-加权马尔可夫预测模型对2010—2021年西安常住人口数进行拟合，并对未来五年西安常住人口数量进行了预测。其结果显示：灰色-加权马尔可夫预测模型相较于灰色G（1，1）模型预测精度提高了79.95%；未来五年西安常住人口数量呈现明显的增长趋势，平均增长率为2.367 9%。此结果对当地政府制定住房供给力度政策具有现实意义。