多胞局域共振型超材料的减振实验研究

吴 昆，高玉强，王立峰，金栋平，胡海岩

（南京航空航天大学机械结构力学及控制国家重点实验室, 南京 210016）

弹性波/声波超材料［1-5］是通过微结构设计实现波动调控并满足相应波动功能的人工材料和复合结构，其研究涉及波动与振动控制［3，6-7］、智能结构设计［8］和先进成型制造［9］等诸多方向，已受到广泛关注。在振动控制领域，传统的隔振装置和减振技术对中频振动展现出良好的控制效果，但在低频区间往往需要较大的安装空间或较复杂的结构设计才能达到所需振动抑制效果［10］。近年来，人们将基于局域共振机理的弹性波超材料设计为一种减振装置［11-13］，通过弹性波的调控和传播衰减，实现对振动能量的抑制隔离。

21 世纪初，Liu 等将局域共振机制［14-15］引入到声子晶体设计中。该研究相比于传统的Bragg 散射机制，可在同等几何尺寸下实现更低频波动带隙。Milton 和Wills［16］提 出 了 一 种 简 洁 的、可 实 现负等效动态质量的物理模型。弹性波在元胞之间传递时会将振动能量转移到内、外质量上，而当元胞的内质量块发生共振时，外质量振动幅值较小，传递到相邻元胞的机械能降低，波动传递一定空间距离后很快衰减，弹性波被阻断。文献［17］对Milton 等提出的物理模型开展实验研究，直观地演示了超材料在低频带隙区间对弹性波的阻断效应。肖勇等［18-19］在杆、梁和板等固体结构中引入局域共振模块，基于多带隙耦合对弹性波带隙和减振频带进行拓宽。文献［20-21］设计准零刚度超材料构型，通过结构参数的变化来实现和调节低频带隙区间。Zhu 等［22］设计含多个局域共振模块的手性超材料梁模型，通过实验构型设计和测试研究了宽频带隙区间内的振动衰减。Pai 等［23-24］建立了含局域共振子系统的超材料梁、板模型，通过频散分析和有限元模拟研究了超材料波动带隙区间的振动抑制效果。Inman 等［25-26］通过参数优化方法对超材料模型进行参数调节，达到增强弹性波阻断性能和提高振动抑制效果的目标。Matlack 等［27］利用3D 打印技术设计加工了一种立方体晶格超材料模型，在实验上实现弹性波低频宽带频率区间的波动衰减；Hu 等［28］通过引入梯度构型设计，在超材料梁结构中实现比周期构型更宽频的振动抑制性能。

然而，将超材料应用到工程振动控制的工作仍然有待进一步研究。本文基于大型可展开空间结构的动力学应用背景［29］，以经典多胞周期超材料为例，设计基于局域共振超材料的减振装置，实验测试其对空间桁架构的振动抑制效果。

1 多胞周期超材料的波动分析

本节基于频散分析给出波动频率与波矢的关系，研究弹性波在周期结构中传播特性。图1 为多胞周期超材料模型，在波传播方向上将元胞周期性排列。红色虚框内为一个元胞，元胞的外部质量为M，内部质量为m。在元胞内，连接内、外质量的弹簧和阻尼器的系数分别为k1和c1。同时，连接相邻元胞的弹簧和阻尼器的系数分别为k0和c0。

图1 一维多胞周期超材料模型Fig.1 Model of one-dimensional periodic multi-cell metamaterial

1.1 局域共振元胞的频散分析

当简谐形式的弹性波在超材料中传播时，将第s个元胞的外部质量和内质量的振动位移分别记为us(t)和vs(t)，可得多胞周期超材料的动力学方程组

根据Bloch 定理，可假设式（1）的复数形式波动解为

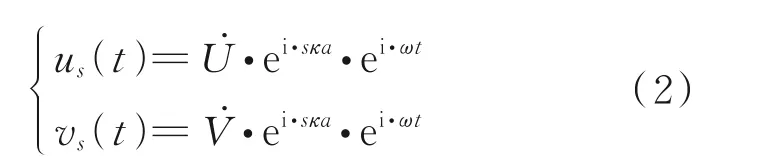
式中：0为零向量；矩阵A和向量Y的具体形式分别为

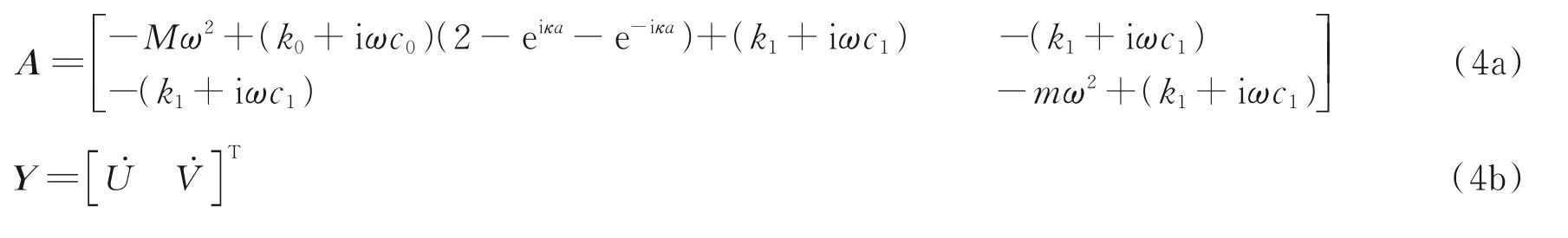
对式（3）求非零解向量Y，可得如下特征值方程

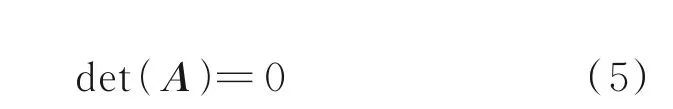
求解式（5）的特征值，即可得到相应的频散关系。

图2 给出了量纲为一波动频率ω˙关于复波数κ的频散曲线，其中ω˙是将波动频率ω关于元胞内质量m的无阻尼共振频率进行了归一化，即

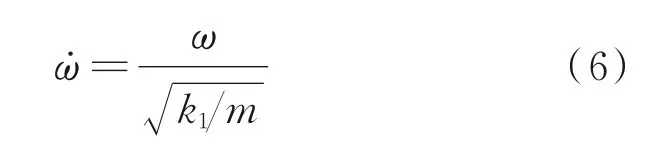
基于表1 给出的超材料结构参数，图2 阴影区间为频散分析所得的波动带隙区。该带隙分布与局域共振频率直接相关，并且在共振频率附近波数虚部更大，反映此频率段对弹性波有更好的阻断效果。值得注意的是，对含阻尼耗散的超材料元胞进行频散分析，代表波动衰减程度的波数虚部大小不仅与所处频率区间相关，还与超材料模型的阻尼系数相关。

表1 含阻尼超材料分析模型的结构参数Table 1 Structural parameters of damped metamaterials analysis model

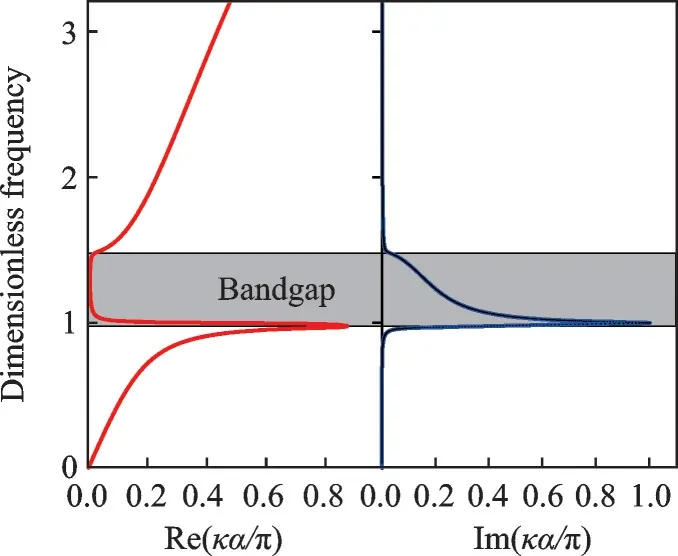
图2 含阻尼超材料元胞的复频散曲线Fig.2 Complex dispersion curves of metamaterial unit cell with damping

1.2 多胞周期超材料的波动传递率分析

当简谐行波在周期超材料中传播时，若不考虑波的反射，则通过计算相邻元胞的幅值传递率可以评估波动传播情况。对式（1）所示的时域函数进行傅里叶变换，可得频域方程组

式中频域复函数Us(ω)和Vs(ω)分别为时域函数us(t)和vs(t)的傅里叶变换。根据超材料的空间周期性和Bloch 波动解形式，可假设

式中：复函数R(ω)与波动频率相关，而与元胞序号无关。R(ω)的模即为相邻元胞外质量的振动幅值传递率，定义为

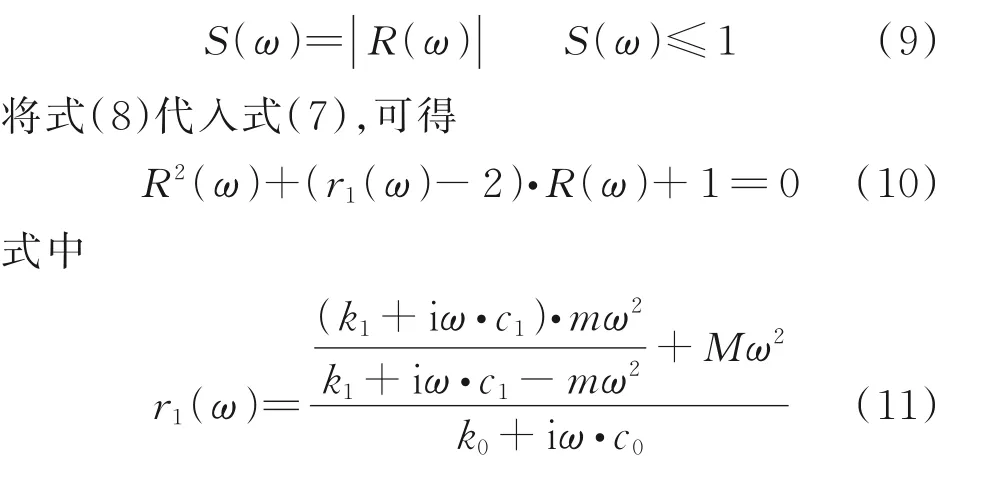
求解式（10），并代入式（9），可得相邻元胞外质量的波动幅值传递率为

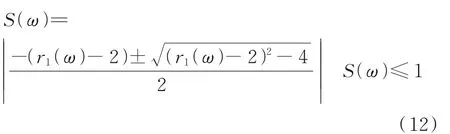
基于表1 给出的结构参数，图3 为单向行波在周期超材料传播时，相邻元胞的波动传递率频谱。由图3 可见，波动传递率在阴影区间频率段大幅降低，反映了弹性波传播的阻断效应。此外，该阴影区间频段与图2 频散分析所得的带隙区间相互吻合。当波动频率处于带隙区时，随着波动传播距离的增加，周期性超材料元胞的振动幅值呈指数形式迅速衰减。然而，由于传播介质空间尺寸的限制，弹性波通常会发生反射，因此有必要计算弹性波在有限尺寸的周期超材料中传播时，超材料各个元胞的振动响应。

图3 周期超材料的相邻元胞波动传递率Fig.3 Wave transmissibility of adjacent unit cell in the periodic metamaterial

1.3 有限尺寸多胞超材料的振动响应数值计算

选取一定周期数的有限尺寸局域共振超材料模型，采用数值计算方法研究弹性波在结构中的传播情况。如图4 所示，模型左侧为位移激励，时域函数记为u0(t)，连接激励处为含N个元胞的超材料模型，在远离激励方向上依次编号为1，2，…，N，右侧连接输出端，时域响应记为uN+1(t)。

图4 含有限个单元的一维周期超材料Fig.4 Model of one-dimensional periodic metamaterial with a finite number of unit cells

在 位 移 激 励u0(t)=u˙0·sinωt下，该 多 自 由 度系统的动力学方程组为

基于表1 的结构参数，选取超材料的元胞个数为N=10，设定两种输出端质量分别为M˙=10M和M˙=0.1M，通 过4 阶Runge-Kutta 数 值 计 算 方法，可得到不同激励频率下输出端M˙的振动响应，其结果如图5 所示。定义输出频响为质量M˙的位移幅值与激励位移幅值u˙0之比的对数比例关系，单位为dB，即

由图5 可见，在共振频率附近的带隙区内，输出端位移传递率远小于0 dB，反映了该频段弹性波传播的阻断衰减。对比两种输出端质量M˙=10M和M˙=0.1M，可发现输出端质量较大时，高频段的波动响应传递率更小，其原因是此时末端质量M˙的振动响应更不容易被激发。

图5 有限尺寸的周期超材料输出端波动传递率Fig.5 Wave transmissibility of response in a finite periodic metamaterial

2 空间桁架结构的振动抑制应用

2.1 多胞周期超材料的实验构型设计

参照图4 的有限个周期多胞超材料模型，图6给出对应的结构构型设计和3D 打印成型实验件。由于空间尺寸限制，多胞超材料实验件的元胞个数取为N=5。元胞外部质量和结构框架由光敏树脂一体成型，元胞中间嵌入圆柱体金属块充当振子，弹簧和阻尼器的连接模块通过薄梁的弯曲变形来等效对应的刚度和阻尼系数。表2 给出了多胞超材料实验装置的设计结构参数。

图6 多胞超材料的实验构型Fig.6 Experimental configuration of a multi-cell metamaterial

表2 减振实验装置的设计参数Table 2 Design parameters of experimental facility for vibration attenuation

图7 给出空间桁架结构减振的实验装置，它由带关节非线性约束的立方体桁架结构、超材料隔振装置和振动测试设备等组成，主要包括激振器1台、数据采集系统1 套、功率放大器1 台、加速度传感器4 个、桁架悬挂装置和超材料悬挂装置各1 个，超材料隔振装置两端分别连接激振器和立方体桁架。其中空间桁架单元由12 根杆件、8 个端点3 向连接关节和4 根面对角扭簧拉索构成，具有轻质高强、结构灵活、宜于展开和收拢等优点。工程中常常将桁架单元沿一个方向或两个方向周期性延伸或者进行环形分布，结构尺度可达101～102m 量级，所得大型桁架结构的动力学特性十分复杂，具有挠性、低刚度、弱阻尼、频率低和模态密集等特性［29］。一旦遇到外界扰动，扰动产生的弹性波在整个空间桁架的杆和关节中传播并且衰减缓慢，对航天器定位和结构稳定性带来严重影响。对于沿一个方向延拓的空间周期桁架，多个面外和面内振动频率分布密集，从1 赫兹到几十赫兹不等，与选取的桁架周期数以及扭簧调节预紧力有关；对于环形桁架结构［30］，前几阶径向振动的频率分布从0.6～30 Hz。值得注意的是，为了在有限空间内实现桁架单元的低频振动抑制，同时缩小减振装置的尺寸，将超材料元胞内部的薄梁采用Z 型折叠设计，以降低等效的弹簧刚度和元胞的局域共振频率。空间桁架单元的质量为3.0 kg，3D 打印的多胞周期超材料框架质量约为0.148 kg，在不明显增加结构附加质量的前提下，对受扰动的空间桁架结构在5～60 Hz 频率区间进行减振实验测试。

图7 减振应用实验装置Fig.7 Experiment setup for vibration attenuation

如图7 左图所示，在空间桁架远端安装3 个加速度传感器，用于测量X-Y-Z这3 方向的加速度振动响应。空间桁架和超材料减振装置分别用柔性绳索和橡皮筋悬挂并保持水平，再将激振器、多胞超材料和空间桁架固定连接并保持在同一水平面。整体实验装置在激励前达到静态平衡，从而可忽略重力对结构振动的影响。除结构阻尼外，还忽略了其他摩擦阻尼的影响。设置激振器输入激励信号为正弦形式，激励方向为X方向，采用固定激励频率和慢速扫频两种激发方式，由弹性波通过超材料传递到空间桁架，引起其远端关节的振动响应。在激励位置和桁架远端关节3 方向上，采集各自的加速度信号，分别得到输入激励和输出响应的时域历程，对时域信号处理后获得加速度传输率频谱。

2.2 空间桁架振动抑制的实验结果

首先，采用定频正弦位移激励，分别选取5 Hz和17.5 Hz 两个频率点，记录立方体桁架的3 向加速度时间响应，其结果如图8 所示。由图8 可见，在频率5 Hz 的正弦激励下，X方向的振动能量通过弹性波传递到柔性空间桁架后，在X、Y、Z这3 个方向上均引起桁架的结构振动，振动能量也因此分配在3 个方向上。作为对比，当激振器施加频率17.5 Hz 的正弦激励时，空间桁架远端关节3 方向的振动幅值几乎可以忽略。这表明，此时弹性波难以传播到空间桁架上。

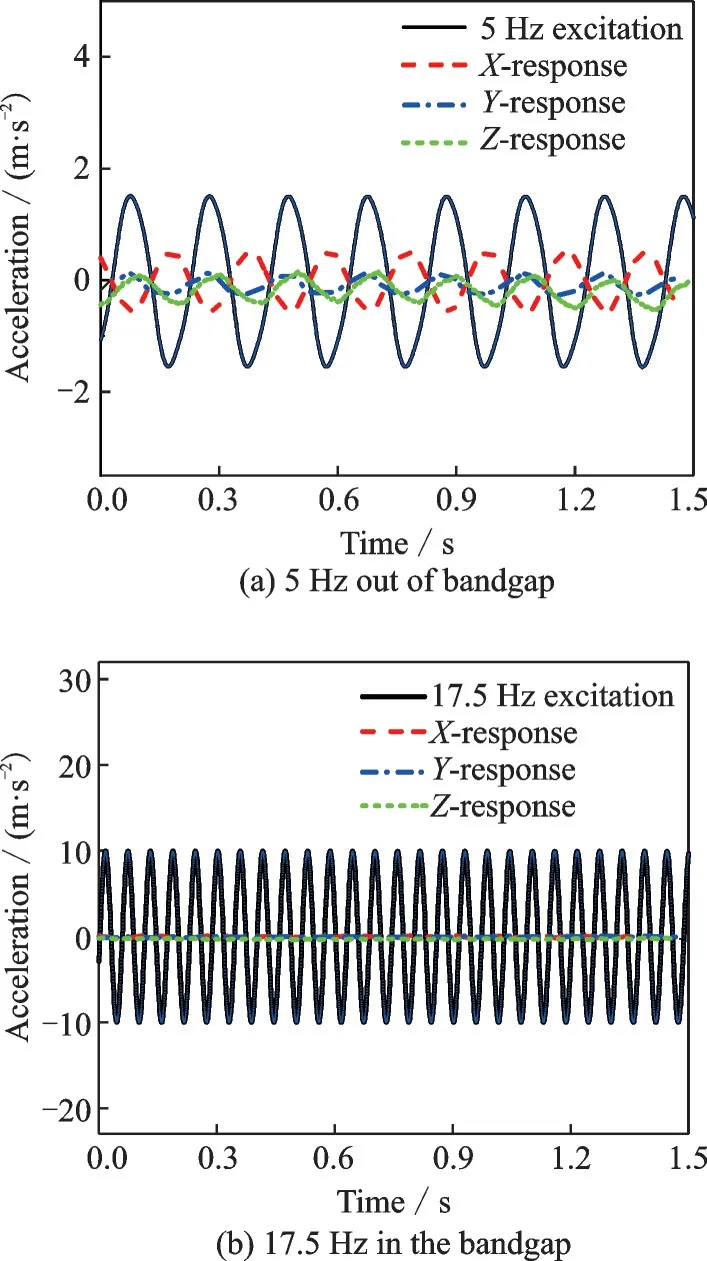
图8 空间桁架的XYZ 方向加速度时域响应Fig.8 Three-dimensional accelerations of the space truss in time domain under excitations

之后采用扫频激励方式，设定频率区间从5～60 Hz，图9 展示了桁架结构X、Y、Z这3 个方向上的加速度幅值传输率。对比3 个方向的振动响应可发现，在较高频率区间X方向的振动幅值远大于另外两个方向，其原因在于X方向为施加激励的方向。在15～45 Hz 频率区间，空间桁架的加速度相比于其他频率段有明显降低，表明振动能量传递到空间桁架受到较明显阻断。综合3 个方向的加速度幅值，可得全加速度传递率频谱，其结果如图10所示。从图10 可见，从5～60 Hz 的整个低频区间，空间桁架的振动响应均得到一定程度的抑制。特别地，在带隙区间15～45 Hz 段，桁架的振动响应传递率低于-30 dB，并且最大衰减程度可达近-40 dB。这表明，所设计的超材料装置在低频区间具备良好的波动阻断效果，可达到空间桁架振动抑制的应用目标。

图9 空间桁架XYZ 方向的加速度传输率频谱Fig.9 Transmissibility spectrum of three-dimensional accelerations of the space truss

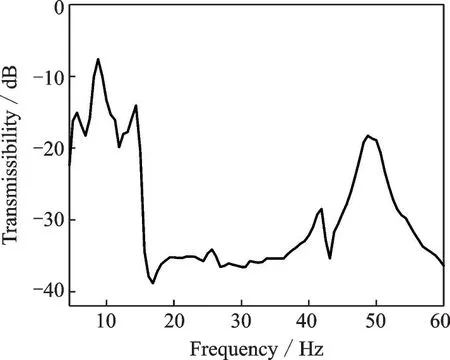
图10 空间桁架全加速度的传递率频谱Fig.10 Transmissibility spectrum of total accelerations of space truss

3 结 论

本文针对空间桁架结构的减振需求，基于对局域共振型周期超材料的波动分析，设计了一种较为轻质的多胞超材料实验件构型，可在15～45 Hz 的频率区间内降低空间桁架的振动幅值达30 dB，部分频段衰减可达近40 dB。实验表明，在不明显增加附加质量和安装空间的前提下，多胞周期超材料对立方体柔性桁架展现出良好的减振应用效果。