高速列车车轮与高速道岔可动心轨接触分析
2022-11-02田志鹏邹小春
张 军,田志鹏,牛 岩,马 贺,邹小春
(北京建筑大学 城市轨道交通车辆服役性能保障北京市重点实验室,北京 100044)
0 引 言
道岔是列车实现轨道转换重要的线路设备,对列车的运行速度和安全有重要影响[1]。列车在通过道岔区段时,轮轨垂直方向的动力不平顺比水平方向高出很多。因此,与普通线路相比,道岔区的养护工作更大,使用寿命更短[2-4]。车轮与道岔型面的合理匹配,对提高列车行驶稳定性、改善列车通过曲线的能力、降低轮岔接触力和磨损、提高轮岔使用寿命及保证列车运行安全具有重要意义。
在道岔区动力学方面,大量学者通过建立动力学模型,对列车通过道岔区的安全性、平稳性及动力学响应进行了分析[5-7];还有学者通过动态仿真模型,对道岔区心轨的关键型面进行优化[8-10]。
在道岔区静力学方面,有学者对高速道岔转辙器区段的轮轨接触力学行为进行了研究[11];王大奎等[12]通过实际测量可动心轨及车轮型面,计算了不同车轮在心轨不同位置处的接触状态;温泽峰等[13]采用数值分析法,对2种不同型面的轮对与钢轨滚动接触时的接触几何、蠕变率和摩擦功进行了分析;M.WIEST等[14]通过建立4种不同的轮岔接触模型,为研究轮轨接触区的弹塑性结构和蠕滑提供了理论依据。
以上成果对研究道岔区轮轨动态相互作用及轮轨接触行为具有重要意义,但以往研究大多对固定辙叉进行分析,对因列车长期运行导致车轮型面改变,进而引起高速道岔可动心轨区段轮轨接触状态变化的分析较少。对此,笔者以60 kg/m钢轨18号可动心轨道岔心轨部分为研究对象(图1),对CRH5型动车车轮与可动心轨的几何形状进行实地测量并建立三维有限元模型,研究不同车轮与可动心轨的接触状态,为进一步优化可动心轨型面提供参考。

图1 60 kg/m钢轨18号可动心轨道岔
1 车轮与可动心轨计算模型建立
为分析车轮由长心轨运动到短心轨的接触过程,分别建立了标准及磨耗后车轮与磨耗后心轨的三维有限元接触模型。通过采集大量CRH5型动车车轮型面并进行筛选,选出磨耗量最大的型面,记为磨耗后车轮型面,如图2。相较于标准车轮,磨耗后车轮的轮缘及踏面均产生磨耗,磨耗量分别为5.96、0.70 mm。

图2 标准与磨耗后车轮型面比较
利用钢轨型面测量仪,对可动心轨轨顶型面进行测量。由于可动心轨为变截面结构,因此选取心轨关键截面进行测量。以可动心轨尖端为基准,取距可动心轨尖端220~300 cm的区段,每隔20 cm对钢轨型面进行一次测量,所测得的可动心轨型面如图3。
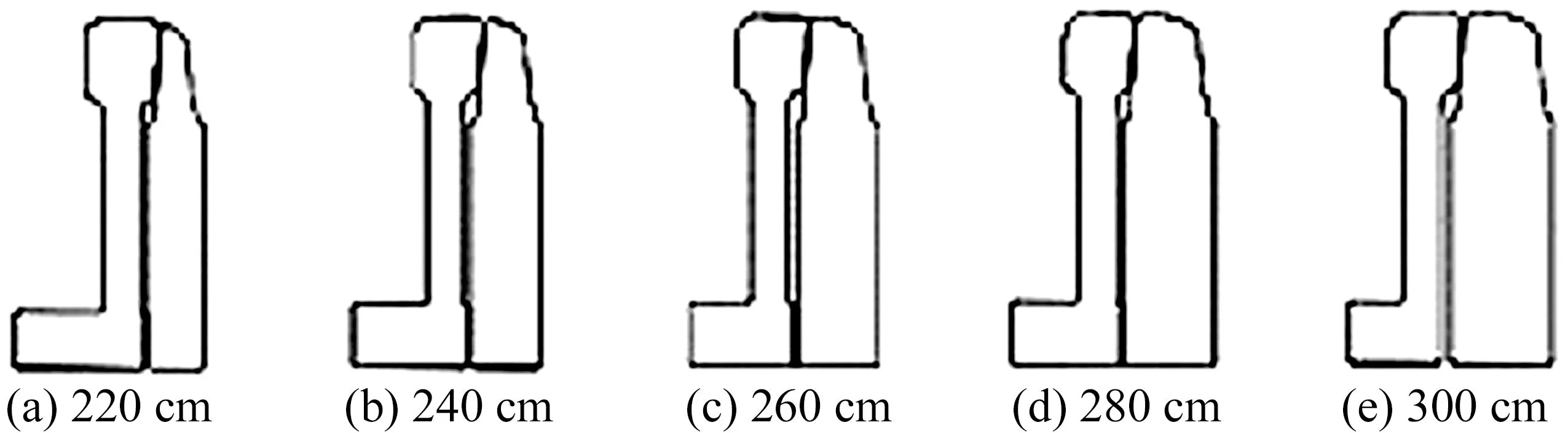
图3 可动心轨型面
将测得的可动心轨型面和不同车轮进行匹配,建立距离心轨尖端230、240、250、260、270、280、290 cm的轮岔接触有限元模型。图4为车轮-可动心轨接触有限元模型,列车车轮直径为915 mm。由于车轮与可动心轨接触,接触区应力远大于非接触区应力,为获得较为清晰的结果,同时节省计算时间,在网格划分时,接触区网格密度较小,非接触区密度逐渐变大,接触区单元网格的最小边长为1 mm。车轮有限元模型共62 693个节点,58 062个单元;可动心轨有限元模型共28 539个节点,25 137个单元。

图4 轮轨接触三维有限元模型
建模时车轮材料弹性模量取200 GPa,泊松比0.3,屈服极限600 MPa;可动心轨材料弹性模量取210 GPa,泊松比0.3,屈服极限490 MPa,车轮与可动心轨材料本构模型采用应力-应变双线性模型,如图5。轮轨间摩擦系数为0.3。

图5 车轮与可动心轨材料本构模型
可动心轨及标准轨底部采用固定约束,长心轨与短心轨间施加绑定约束,约束车轮两端横向、纵向位移,并对车轮的转动进行约束,在车轴轴箱处施加垂向的集中载荷8.5 t(动车满载轴重17 t)。
2 标准车轮与可动心轨接触分析
2.1 标准车轮与可动心轨接触斑分析
图6为距可动心轨尖端240、250、260 cm处轮岔接触斑。距可动心轨尖端240 cm处,车轮仅与长心轨接触;在距可动心轨尖端250 cm附近,车轮与长心轨和短心轨共同接触;在260 cm处,车轮只与短心轨接触,此时车轮已完全从长心轨过渡到短心轨。标准车轮与可动心轨匹配时,接触斑呈椭圆状,形状狭长。

图6 标准车轮与可动心轨接触斑
表1为标准车轮与可动心轨接触斑的面积及纵、横向长度,可知接触斑面积最大为111.40 mm2在距可动心轨尖端250 cm处。在车轮完成从长心轨向短心轨过渡后,接触斑面积逐渐增大,这是因为随着短心轨轨顶不断变宽,车轮与短心轨接触更加充分。

表1 标准车轮与可动心轨接触斑情况
2.2 标准车轮与可动心轨等效应力分析
图7为距可动心轨尖端240、250、260 cm处标准车轮与可动心轨接触等效应力分布。距可动心轨尖端240 cm处,最大等效应力主要分布在长心轨上,其值为629.4 MPa;距可动心轨尖端250 cm处,车轮同时与长短心轨接触,长心轨与短心轨都有等效应力分布,但最大等效应力由长心轨转移到短心轨上,其值为556.8 MPa;距可动心轨尖端260 cm处,短心轨上的最大等效应力继续增大,其值为595.5 MPa。
在距可动心轨尖端240、250、260 cm处,最大等效应力从长心轨向短心轨转移,短心轨上的最大等效应力值不断增大。产生这种现象的原因是随着距可动心轨尖端的距离增加,短心轨轨顶不断增宽加高,使短心轨逐渐承受轴重。
表2为标准车轮与可动心轨在不同位置处接触时最大等效应力。接触斑面积在距离可动心轨尖端250 cm处最大,等效应力值最小,为556.8 MPa;接触斑面积在距离可动心轨尖端290 cm处相对较小,且接触斑形状狭长,车轮载荷施加在小面积钢轨上,因此等效应力在此处最大,为662.7 MPa。
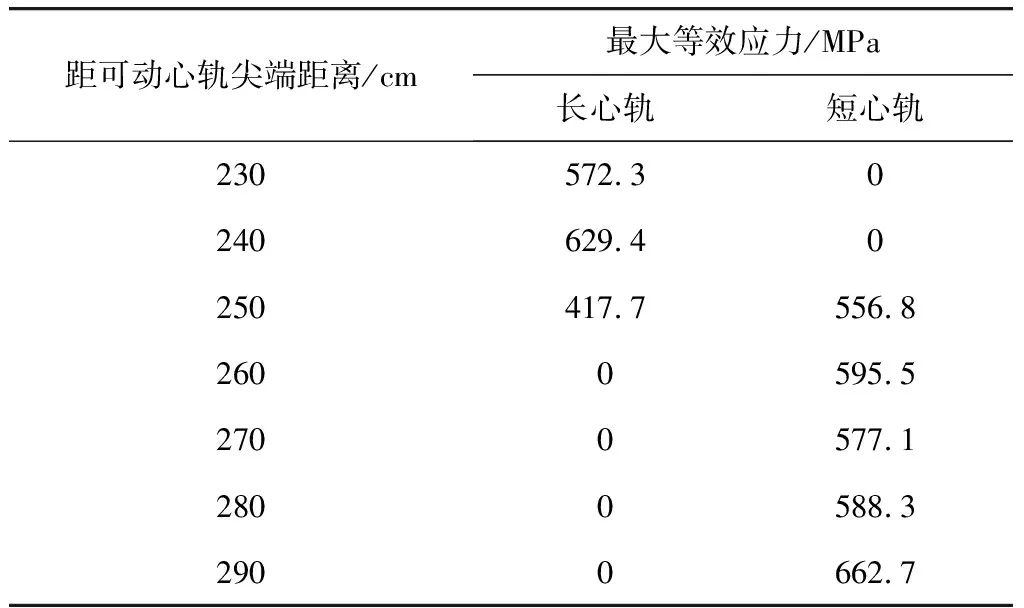
表2 标准车轮与可动心轨接触最大等效应力
在距可动心轨尖端230至290 cm区段关键位置处,可动心轨材料的屈服极限值均低于轮轨接触产生的最大等效应力值,列车在反复通过可动心轨区段时,车轮频繁与可动心轨进行接触,可动心轨会产生磨耗,严重甚至会造成剥离等破坏。
2.3 标准车轮与可动心轨等效塑性应变分析
表3为标准车轮与可动心轨接触最大等效塑性应变值。距可动心轨尖端240 cm处等效塑性应变值最大,为1.205×10-2,距可动心轨尖端250 cm处等效塑性应变值最小,为8.063×10-3。在距可动心轨尖端230至290 cm区段关键位置处,车轮与可动心轨接触均产生等效塑性应变,可动心轨会产生磨耗。

表3 标准车轮与可动心轨接触最大等效塑性应变
3 磨耗后车轮与可动心轨接触分析
3.1 磨耗后车轮与可动心轨接触斑分析
图8为距可动心轨尖端240、250、260、270 cm处磨耗后车轮与可动心轨接触斑。较标准车轮与可动心轨接触相比,磨耗后车轮从长心轨向短心轨过渡区段相对延长。在距可动心轨尖端240 cm处,车轮只与长心轨接触;与可动心轨尖端相距250至260 cm区段,车轮与长、短心轨共同接触;与可动心轨尖端相距270 cm处,车轮只与短心轨接触,且接触斑逐渐向短心轨外侧移动,此时车轮完成了从长心轨向短心轨的过渡。

图8 磨耗后车轮与可动心轨接触斑
表4为磨耗车轮与可动心轨接触斑的面积及纵、横向长度。接触斑面积在与可动心轨尖端相距230 cm处最大,为119.36 mm2。磨耗后车轮与可动心轨接触斑沿纵向的半轴长度较沿横向的半轴长度大,但相差数值相对较小。因此,磨耗后车轮与可动心轨的型面匹配相较标准车轮更加良好。

表4 磨耗车轮与可动心轨接触斑情况
图9为距可动心轨尖端290 cm处接触斑。此处短心轨顶面上的接触斑出现了不连续现象,接触斑分成了两部分,车轮与短心轨间产生了两点接触,这是轮轨接触中的一种常见状态。产生这种现象的原因,是磨耗后的车轮与这段钢轨的接触区内存在纵向“凹陷”,“凹陷”内所对应的区域与车轮并不产生接触,因此形成了条形间断接触斑。

图9 距可动心轨尖端290 cm处接触斑
3.2 磨耗后车轮与可动心轨接触等效应力分析
图10为距可动心轨尖端240、250、260、270 cm处可动心轨等效应力分布。距可动心轨尖端240 cm处,最大等效应力分布在长心轨上,其值为569.0 MPa;与可动心轨尖端相距250、260 cm处,车轮与长、短心轨共同接触,但均在短心轨上产生最大等效应力,在260 cm处短心轨上最大等效应力相对250 cm处较小;距可动心轨尖端270 cm处,车轮已完成过渡,等效应力完全转移到短心轨上,此时最大等效应力为605.1 MPa。

图10 不同接触位置的心轨等效应力图
表5为磨耗后车轮与可动心轨在不同位置接触的最大等效应力。距可动心轨尖端270 cm处最大等效应力值最大,为605.1 MPa;在距可动心轨尖端230 cm处,接触斑面积相对最大,此处最大等效应力值最小,为501.4 MPa。
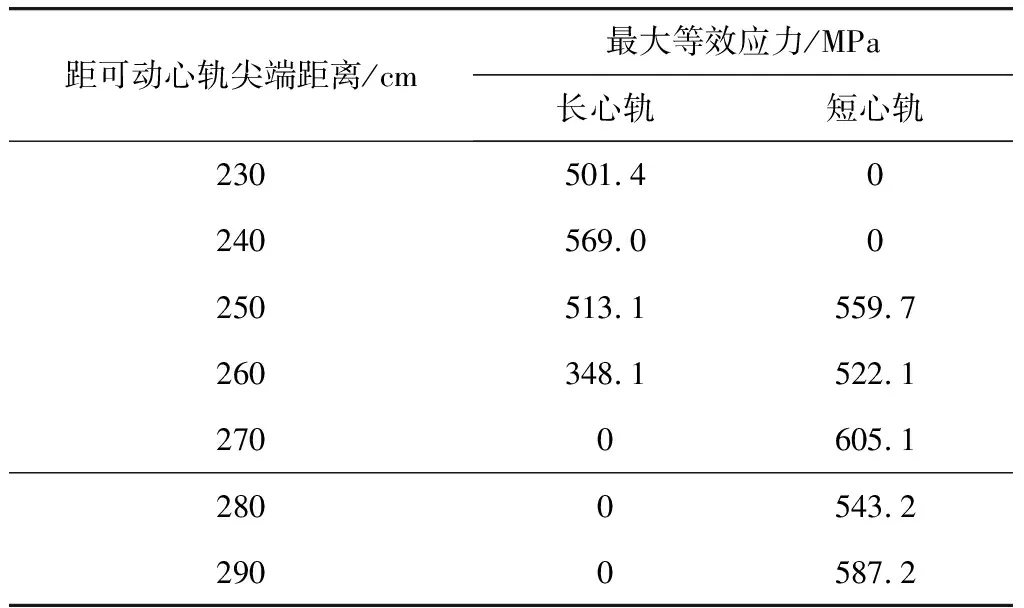
表5 磨耗后车轮与可动心轨接触的最大等效应力
3.3 磨耗后车轮与可动心轨等效塑性应变分析
表6为磨耗车轮与可动心轨接触最大等效塑性应变值。距可动心轨尖端270 cm处,轮轨接触最大等效塑性应变值最大,为9.759×10-3(最大值位于270 cm处短心轨,250 cm处数值并非长短心轨相加,两者是独立的);距可动心轨尖端230 cm处,最大等效塑性应变值最小,为5.326×10-3;距可动心轨尖端250 cm处,长短心轨同时产生塑性应变,这是由于此处为车轮过渡区段,车轮与长短心轨共同接触,使长短心轨同时产生磨耗。
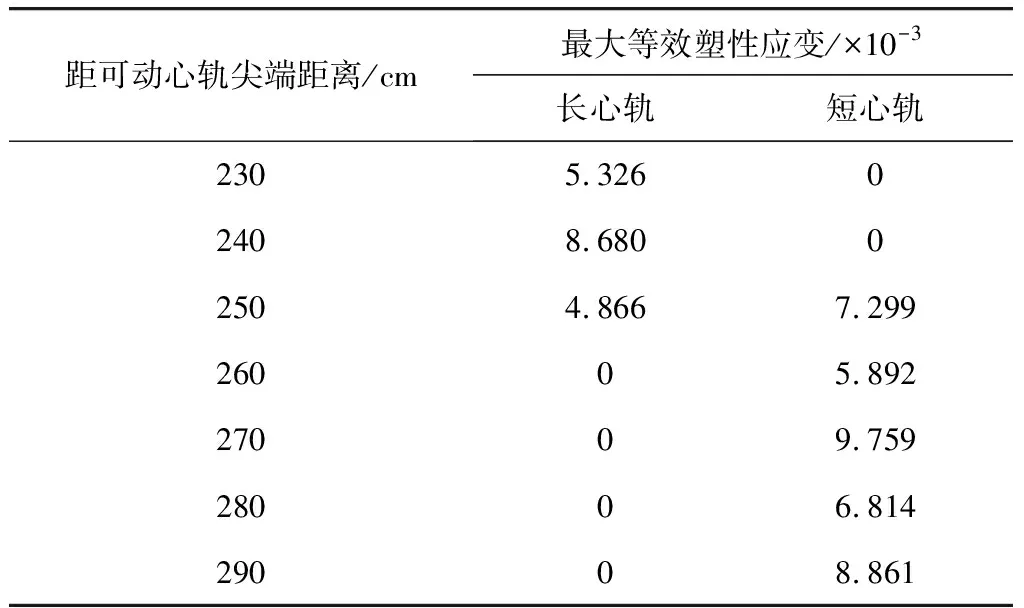
表6 磨耗车轮与可动心轨接触最大等效塑性应变
4 标准和磨耗车轮与可动心轨接触对比
4.1 接触斑对比分析
图11为标准和磨耗车轮与可动心轨接触斑面积变化曲线。通过对比标准和磨耗后的车轮在相同截面位置的接触斑总面积可以发现,与标准车轮相比,磨耗后车轮与可动心轨的接触斑面积更大。这是由于经列车运行,车轮踏面发生磨耗,磨耗后车轮踏面形状和可动心轨匹配更好,因此接触斑面积有所增大。
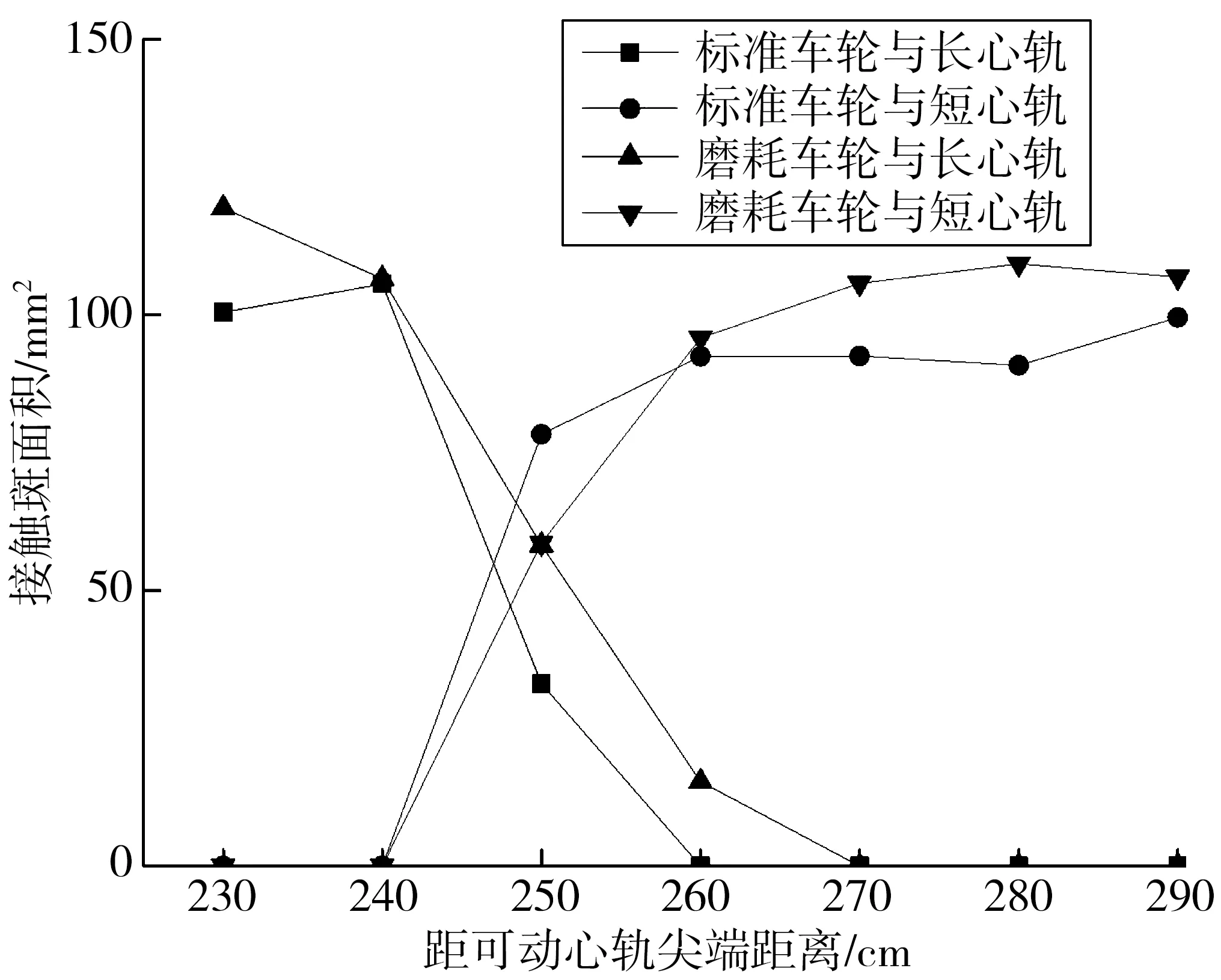
图11 接触斑面积变化曲线
4.2 等效应力对比分析
图12为标准车轮与磨耗后车轮与可动心轨接触最大等效应力变化曲线。在车轮同时与长短心轨发生接触前,最大等效应力值均呈先增大后减小的趋势,同时接触后,钢轨等效应力均成先增大再减小,后再增大的趋势。此处以车轮与长短心轨同时接触为分界,标准车轮在250 cm处同时接触,260 cm处结束;磨耗车轮在250 cm处同时接触,在270 cm处结束,后同。除距可动心轨尖端250 cm和270 cm处外,与标准车轮相比,磨耗后车轮与可动心轨接触的最大等效应力值更小。这是由于相对标准车轮,磨耗后车轮与可动心轨接触斑面积较大,等效应力值相对较小。相比于标准车轮,磨耗车轮与可动心轨接触状态更加良好,但两种接触情况的最大等效应力值仍大于可动心轨材料的屈服极限,在车轮与钢轨的反复接触过程中,同样会造成钢轨磨耗。

图12 最大等效应力变化曲线
4.3 等效塑性应变对比分析
图13为标准车轮与磨耗后车轮与可动心轨接触最大等效塑性应变曲线。在车轮同时与长短心轨发生接触前,最大等效应变值均呈先增大后减小的趋势,同时接触后,等效应变值均成先增大再减小,后再增大的趋势(同4.2节),其变化趋势与轮轨接触最大等效应力变化趋势相同。除距可动心轨尖端270 cm处外,与标准车轮相比,磨耗后车轮与可动心轨接触的最大等效塑性应变值更小。这是因为磨耗后车轮与可动心轨等效应力值较小,相比于标准车轮,磨耗车轮与可动心轨接触状态更加良好。但两种车轮与可动心轨接触均产生塑性应变,钢轨均会产生磨损变形。
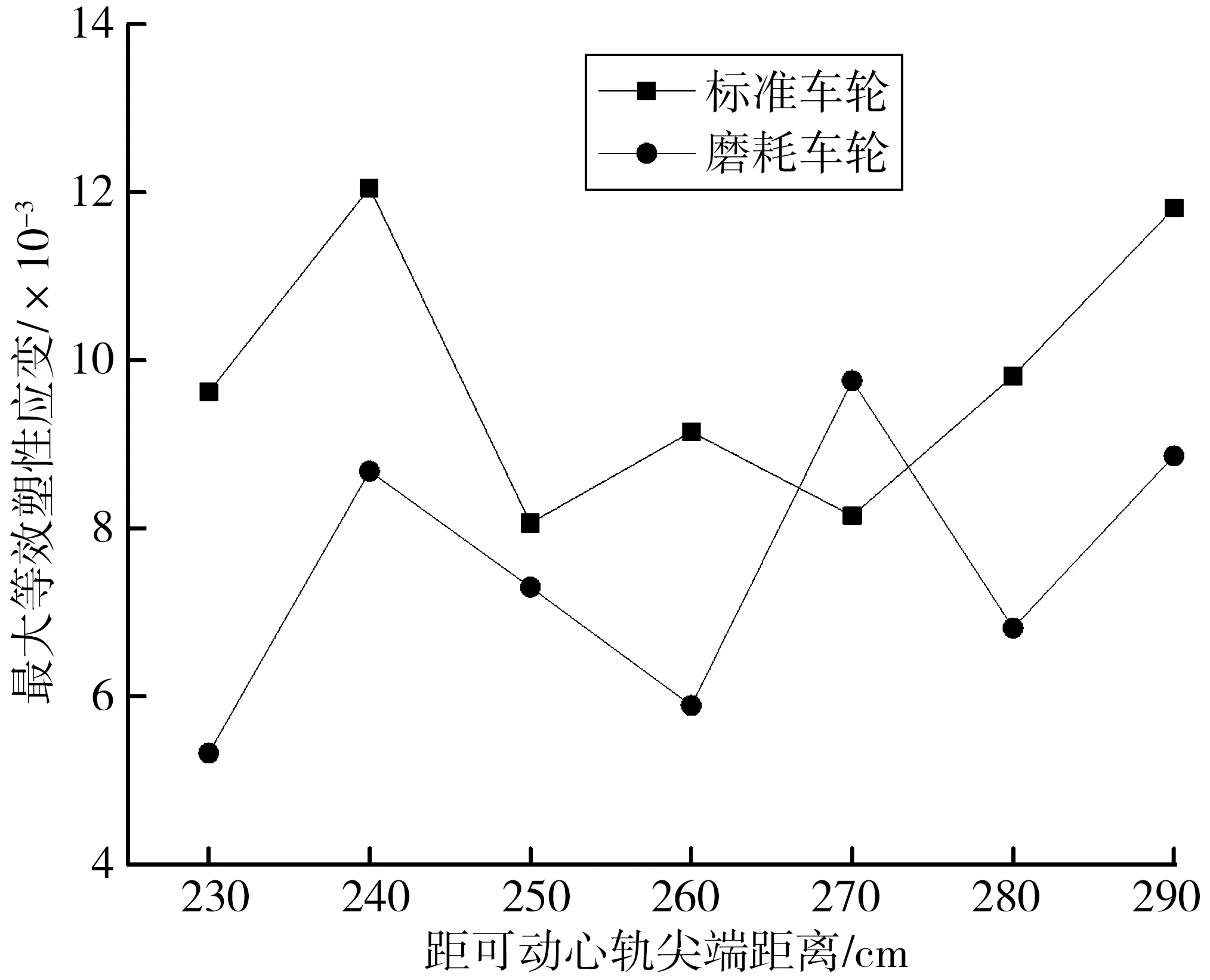
图13 最大等效塑性应变曲线
5 结 论
笔者在前人研究的基础上,通过建立标准XP55车轮和磨耗后车轮与60 kg/m钢轨18号高速道岔可动心轨的接触模型,利用有限元分析方法求解计算,得出接触斑形状及面积、等效应力的大小及变化规律。根据计算结果得出以下结论:
1)列车通过可动心轨区段时,均由长心轨向短心轨过渡,且相较于标准车轮,磨耗后车轮的过渡区段相对延长。
2)标准车轮与可动心轨的接触斑面积均小于磨耗后车轮与可动心轨的接触斑面积。标准车轮与可动心轨匹配更易发生应力集中以致加剧轮轨磨损。
3)标准车轮和磨耗后车轮与可动心轨接触时,在可动心轨表面均产生应力集中,且最大等效应力值均大于钢轨材料的屈服极限,可动心轨出现塑性形变。
