空气热机平衡点的快速判定方法

全泓达,盖 磊

(中国海洋大学 物理与光电工程学院，山东 青岛 266100)

热机是将热能转换为机械能的仪器.法国青年工程师卡诺从理论上对理想热机的工作原理进行研究，提出了一种理想的由2个等温及2个绝热过程的循环，称为卡诺循环，并在1824年提出了卡诺定理，为后来热力学第二定律的建立奠定了基础，为提高热机的效率指明了方向，为热力学的发展做出了杰出的贡献[1-3].

由于热机的整个装置处于动态平衡，获取精准的静态状态数据需要较长的判断时间，因此本文主要基于空气热机实验中验证卡诺定理的静态测量法，探索了快速判断平衡点的方法.

1 实验设备及原理

1.1 空气热机实验仪

实验采用世纪中科的ZKY-RJ空气热机实验仪，实验由空气热机电加热器进行加热，并由空气热机测试仪得到冷端温度、热端温度、转速、气缸压力以及气缸体积等实验数据，并经过实验通信器面板传回电脑进行数据显示.

1.2 静态测量法验证卡诺定理

热机每次循环从热源吸收的热量

(1)

其中，n为热机转速，ΔT为冷热端温差.因此热机效率η可表示为

(2)

其中，A为气体对外所做的净功，即P-V图中曲线所围面积.由于式中的变量均可以在实验中测量得到，因此通过观测不同冷热端温度时的nA/ΔT与ΔT/n的关系即可验证卡诺定理.

测量式子(2)中的参量有2种方法：静态测量法和动态测量法.静态测量法是在电压档位一定时，在系统稳定后测量得到的平均值，可以表示在一定的冷热端温度时的关系.热机稳定工作是指冷热端在一定的温度下，保持一定的效率，即在每次循环中热机对外做功近乎不变.在一定输入功率下，系统是否达到平衡取决于冷热端的温差和转速，即通过电加热器可以使冷热端温差变大(视冷端温度不变或者变化很小)，而热机每次循环都将从热源吸收热量，使冷热端温差下降.所以二者的平衡即是静态测量法所需要的稳定状态.

实验中判断热机是否平衡需要长时间的数据记录，当转速、冷热端温差在一定范围内上下浮动时(例如n<1 r·s-1，ΔT<5 K)，可判断空气热机达到平衡状态，但判定平衡点的观测时间通常需要10 min甚至更长，从而不利于实验教学.

2 实验设计及步骤

1)打开计算机、测试仪和通信器，加热电源；

2)将电压调至5档，预热仪器使飞轮顺利转动(一般ΔT>80 K)；

3)将电压调回1档，开始计时计数，每隔1 min记录1次T1,ΔT,n和A，直至各项数值在平衡点附近变化(记录时间约1 h)；

4)将电压调至2档重复上述步骤3).

3 数据处理

3.1 数据处理方法的原理

3.1.1 K型均值聚类

K型均值聚类(K-means clustering)是经典的无监督机器学习算法，用于无目标值的数据集[4].K型算法主要是通过迭代来对数据集进行分类.首先在样本中选取任意K个样本作为聚类中心,利用所选取的聚类中心计算各样本与中心间的距离；然后根据获得的最小计算距离重新划分对象.距离一般通过欧式距离Dδ进行度量，表达式如下：

Dδ(xi,xj)=

(3)

其中，xi=(xi1,xi2，…，xip)和xj=(xj1,xj2,…,xjp)表示p维欧几里德空间中的2点.重新计算获得每个样本的均值后，迭代至目标函数值不变或者小于指定阈值.目标函数为平方误差准则函数，表示为

(4)

其中,Ci为数据对象数量，ci表示第i个簇中心.

3.1.2 KNN分类

最近邻节点分类(K-nearest neighbor，KNN)方法是有监督的弱机器学习算法[5],其通过计算预测值与现有样本的闵可夫斯基距离(Minkowski distance)来确定预测所属类别.

闵式距离的表达式为：

(5)

当p→∞时，闵式距离转化为切比雪夫距离(Chebyshev distance)；当p=2时，闵式距离转化为欧几里得距离；当p=1时，闵式距离转化为曼哈顿距离(Manhattan distance).通过闵式距离，可较好表示n维欧几里德空间中2点相对距离.

KNN算法中最为重要的参量为判断类别时采用的样本个数，若选取的样本数量过小，容易受到异常点的影响；若选取的样本数量过大，就会受到样本均衡的影响，所以选取合适的样本数对KNN模型具有重要作用.

本文对实验数据进行KNN分类处理，以获得能较好判断热机是否到达平衡的模型，通过该模型能准确快速地判断空气热机是否达到平衡，从而减少实验时间.

3.2 实验数据处理

为使实验结果具有普适性，消除仪器和档位(加热电压)的偶然性，本文对2台仪器3个档位进行实验，部分原始数据如表1所示.

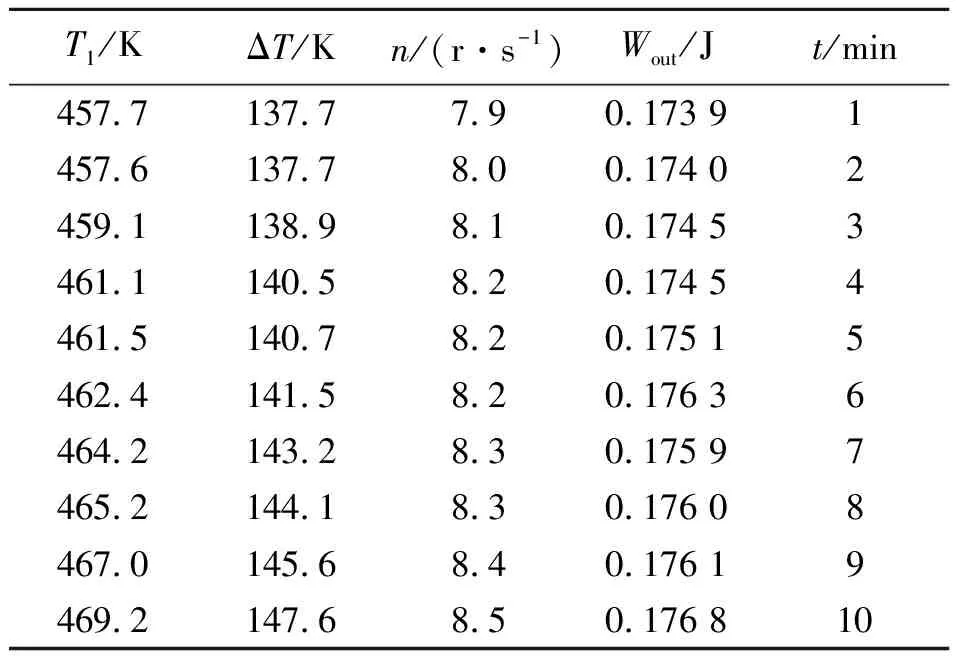
表1 实验原始数据(部分)

由于各项指标的数据单位以及数值大小不同，所以需要对各类数据进行标准化.假设进行分析的指标变量有m个，分别为z1,z2,…,zm，共有n个评价对象，第i个评价对象的第j个指标的取值为aij[6].将各指标值转化为标准化值有

(6)

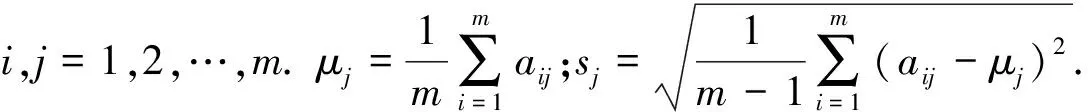
由式(6)可获得各项指标标准化后随时间的变化图线，如图1所示.根据卡诺定理，热机在稳定运行时，其在1个循环内的效率仅跟冷热端温度有关，而在多次循环中，转速与循环次数有关，那么是否平衡也与转速有关.以下将不考虑对外做功对平衡判断的影响.需要补充说明的是，为了获取仅与上述因素有关的热机平衡判定方法，而非对比仪器间差异，所以无需控制仪器A和B都在电压档1和2进行实验测量.

(a)仪器A电压档1

利用得到的标准化数据，进行K型聚类[7]，将欧几里德距离作为K型聚类的判断标准，将数据分为平衡状态与非平衡状态，由此可以获得较为客观公正的平衡点，图2为聚类后的轮廓图.

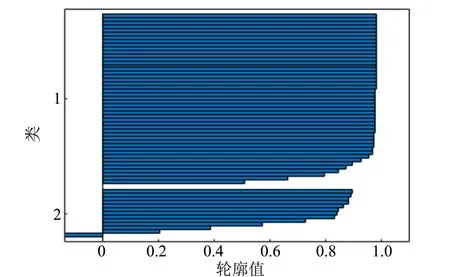
(a)仪器A电压档1

图2中簇1为聚类后认定的平衡状态，簇2为聚类后认定的非平衡状态.通过对轮廓图的分析，可以发现聚类效果较为显著.为了让实验数据更具有信服力，本次实验记录了长时间(远超热机平衡所需时间)的实验数据，所以有大量的平衡状态数据点，而该类型的点能很好地被聚集在一起，形成较为明显的数据边际，说明平衡与非平衡之间存在一定的衡量指标.

然后利用KNN进行分类，将所有数据进行整合，并将加热电压值作为模型建立的特征值.图3和图4为模型的训练结果.

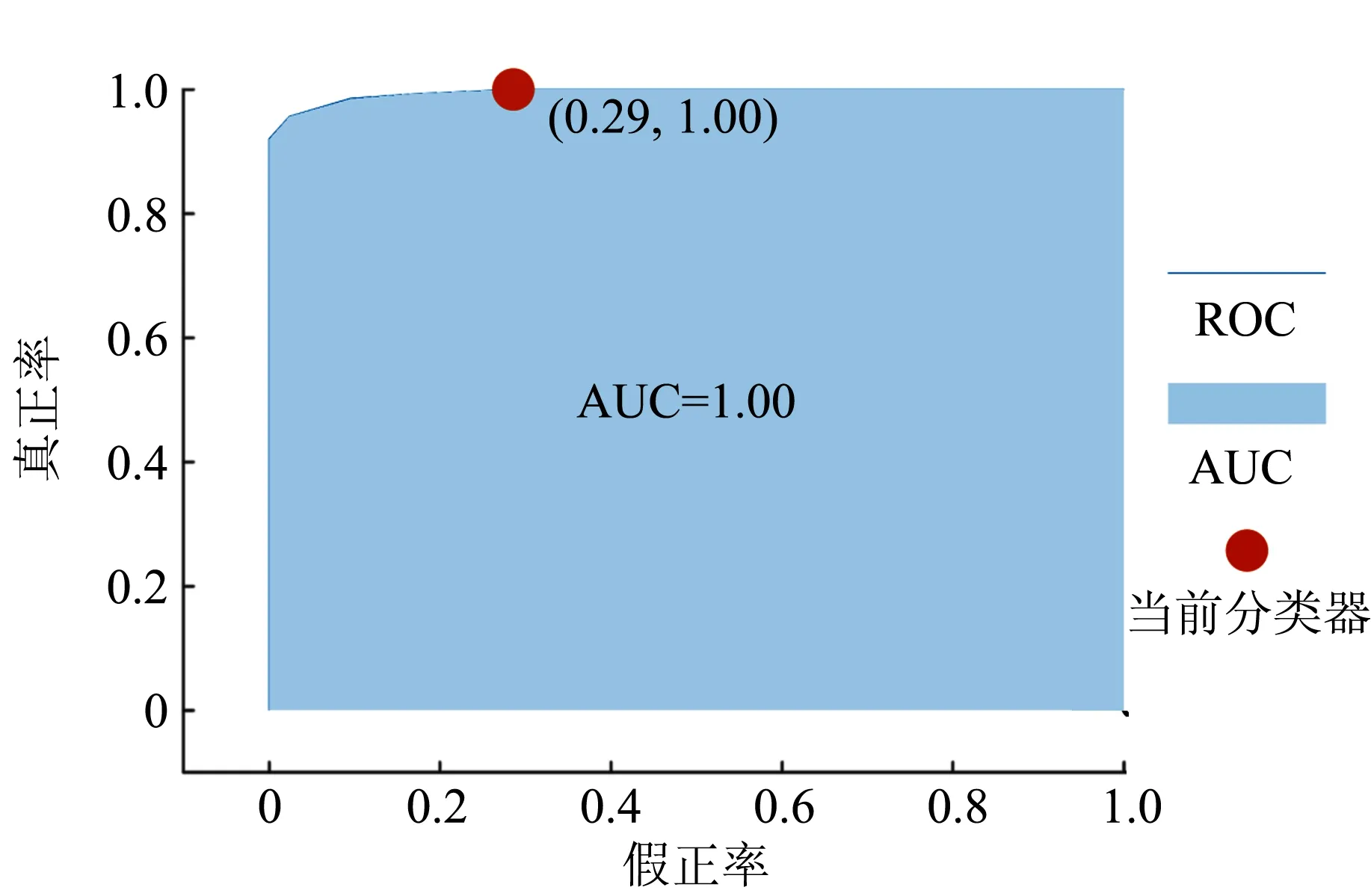
图3 模型ROC曲线与AUC

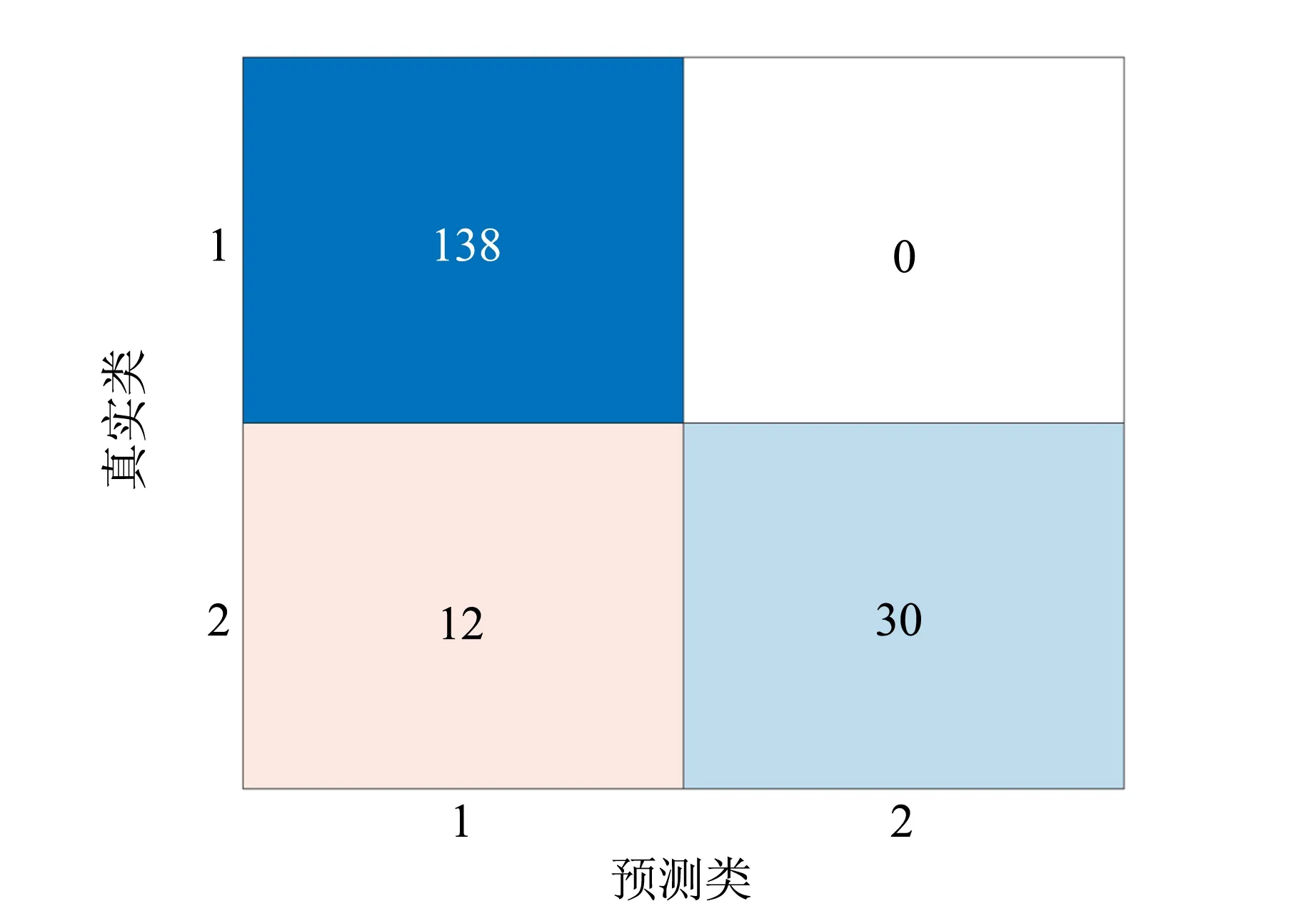
图4 模型混淆矩阵

整体利用5折交叉验证获得的模型准确率达到93.3%，且为了防止过拟合，预留部分数据进行验证，最后效果较好，基本满足预期需求.

图3为模型的ROC曲线(Receiver operating characteristic)，其中AUC[8](Area under curve)接近1，远在超假正率(False positive rate，FPR)等于真正率(True Positive Rate，TPR)的直线上方，接近1个完美的分类器.

图4为模型的混淆矩阵[9]，从矩阵可以看出误判断数量较少，整体能比较好地对平衡与非平衡状态进行分类.

基于以上模型，再次进行5组实验，在不同仪器不同电压档位下各测量60个数据，并将得到的数据放入模型预测系统是否处于平衡状态.为了避免仪器因转速过高而触发保护机制，将最高电压档位设定为4档.

图5是模型对于系统是否达到平衡状态判断，横坐标表示仪器和电压档位，上下阈值为K-means聚类算法得出的平衡点的最大值和最小值，模型所判断出的平衡点落在该范围越多说明模型判定准确性越好.可以看出，模型判断的平衡点基本都集中在平衡范围内.

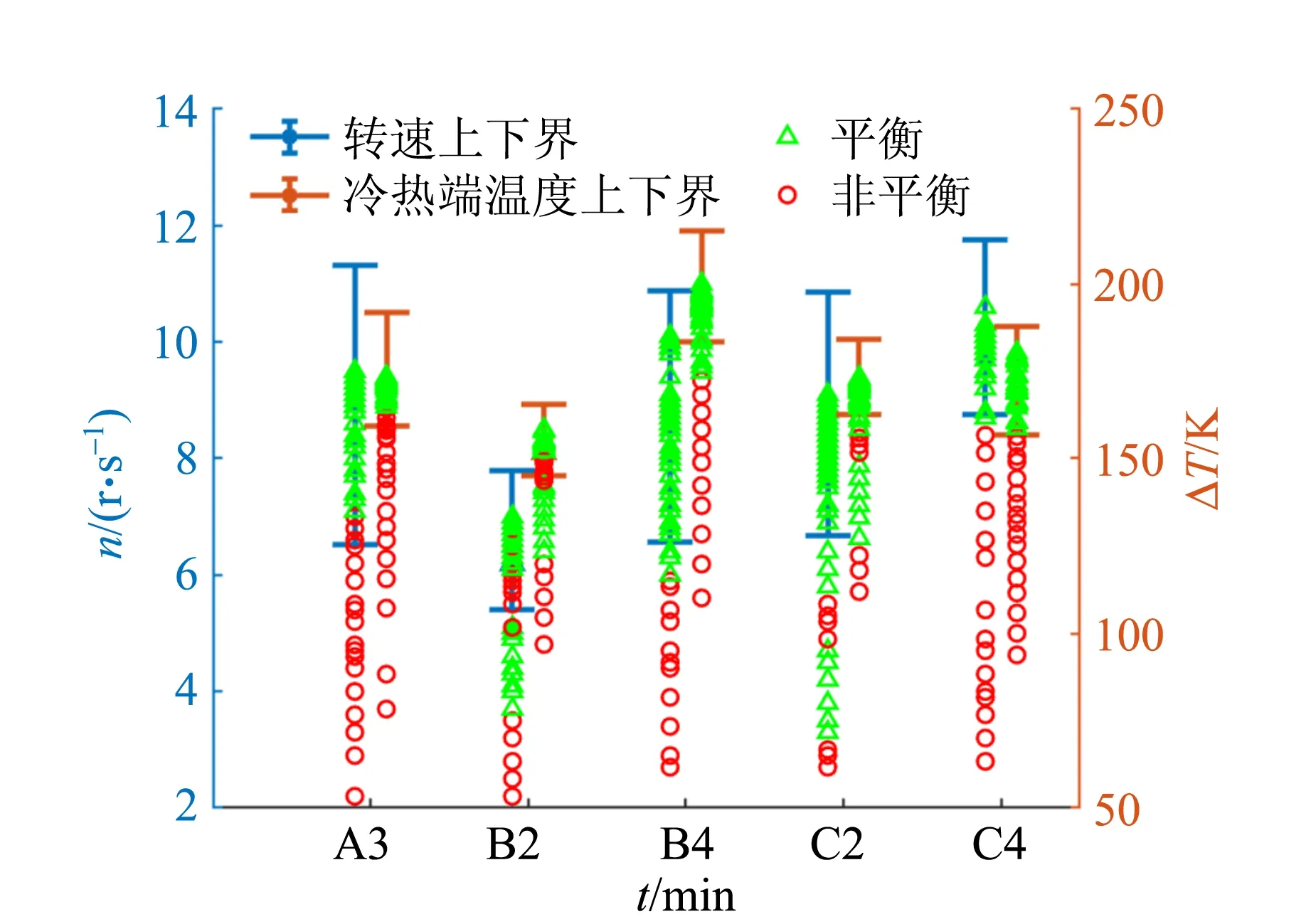
图5 不同仪器、不同电压档位下系统平衡状态的判断结果

图6为C仪器在电压档为4时的转速随时间的判断结果，可看出系统在平衡状态与非平衡状态间的转换位置处于曲线拐点，与真实进入平衡点时间不超过2 min，说明该模型判断效果较好.

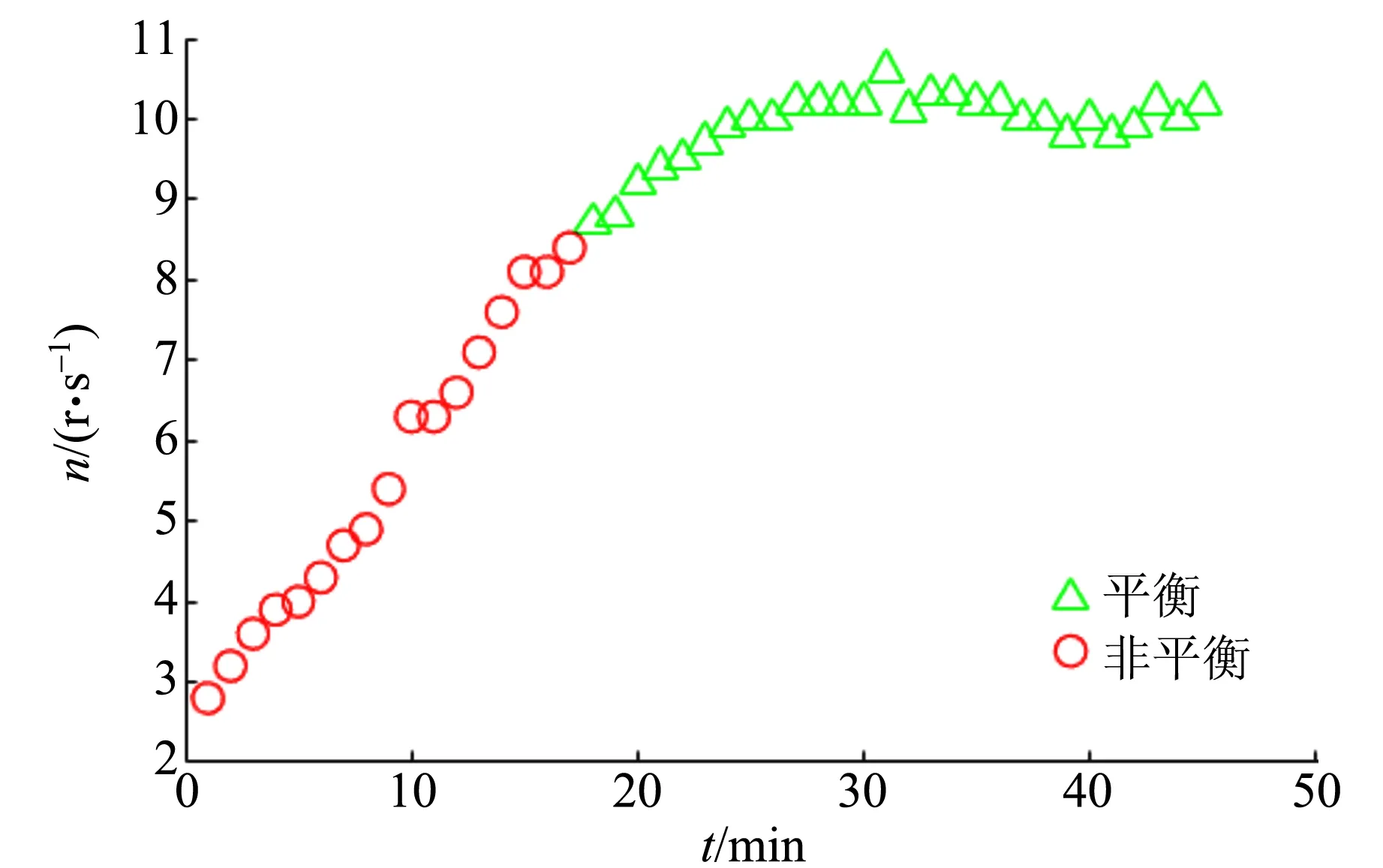
图6 C仪器在电压档为4时转速随时间的判断结果

4 结束语

本文通过对空气热机实验测得的数据进行分析，获得了基于KNN的模型分类器，通过多种指标对模型进行衡量分类都有较好的预测结果.其中，误分类点处于平衡状态与非平衡状态的模糊界线处，从错误预测进入正确预测所需时间不大于2 min，因此误分类相较于接近10 min的主观判断有了大幅度的提升，并具备一定的实用性.将每一时刻获得的数据输入该模型，能得到较好的预测结果.另外，通过K-means聚类算法可以对因测量精度、环境影响、仪器误差、动态平衡等因素带来的数据波动提供较好的参考中心值，从而使得真实值的选取更加准确.