套管居中度计算模型改进

2022-11-01冀梦佳

天然气与石油 2022年5期

俞豪吴朗冀梦佳

1. 长江大学(武汉)石油工程学院,湖北武汉 430100;2. 中国石油集团川庆钻探工程有限公司井下作业公司,四川成都 610500

0 前言

随着油田地质环境的复杂化,钻井难度也随之增加,同时对固井的质量要求也越来越高[1]。在固井过程中,提高水泥浆的顶替效率可以提高固井质量[2],井眼中的套管居中度则是影响水泥浆顶替效率的重要因素[3-4]。若居中度差,套管与井眼之间会形成不均匀的宽窄边,导致钻井液窜槽且顶替不干净,从而严重影响固井质量[5-6]。研究表明,套管居中度大于80%时,水泥浆顶替效率可达95%以上,套管居中度为50%时,水泥浆顶替效率仅为70%[7-9]。所以提高套管居中度,可以有效提高水泥浆顶替效率,从而形成密封性好的水泥环,确保固井质量[10-12]。

许多学者对套管居中度的计算进行了大量的研究,目前国内主流采用的是石油天然气行业标准SY/T 5334—1996《套管扶正器安装间距计算方法》(以下简称SY/T 5334—1996)模型[13],但存在不足。吴疆[14]采用瑞利—里兹方法研究了一维、二维、三维井眼的套管扶正器安放间距计算公式。朱忠喜等人[15]采用三维力学分析方法设计扶正器间距。李黔等人[16]认为计算套管轴向载荷时需考虑摩阻效应，但是他们同样忽视了套管内外液体密度差对居中度的影响。丁保刚等人[7]考虑了套管内外液体密度差和铅垂面上复位力方向的问题并修正了相关公式。谭树人[17]考虑了套管内外液体密度差,且补充了狗腿严重度对径向力的影响，但是套管受力变形公式不够准确,需采用新挠度公式。

本文将在SY/T 5334—1996模型基础上考虑套管内外液体密度差并采用新的挠度公式,同时修正SY/T 5334—1996中偏心距的计算方法,综合前人所考虑的因素建立套管居中度计算改进模型,并且与现场成像测井数据进行比较,验证改进模型的准确度。

1 模型建立

1.1 套管居中度

套管居中度是用来表达套管轴线与井眼轴线之间的位置关系,当偏心距等于0时,套管居中度是100%;当偏心距等于R-r时,套管居中度为0。套管居中度示意图见图1。

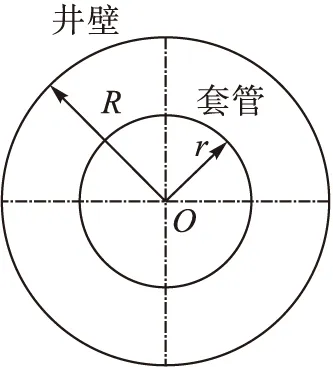
a)居中度为100%a)Casing centering degree is 100%

根据套管偏心距计算套管居中度:

(1)

式中:R为井眼半径,cm;r为套管外半径,cm;e为套管偏心距,cm;ε为套管居中度。

1.2 偏心距

1.2.1 弹性套管扶正器

相邻两只扶正器全为弹性套管扶正器时,套管最大偏心距emax为:

(2)

式中:emax为套管最大偏心距，cm；ev为铅垂面上的扶正器压缩变形量,cm;es为平均井斜狗腿面上的扶正器压缩变形量,cm;δ为套管挠度值。

铅垂面上的弹性套管扶正器压缩变形量:

ev=F(Pv)

(3)

式中:F(P)为弹性套管扶正器压缩变形弹性曲线函数式,即复位力为P时的压缩变形量，cm;Pv为铅垂面上的复位力,N。

平均井斜狗腿平面上的弹性套管扶正器压缩变形量:

es=F(Ps)

(4)

式中:Ps为平均井狗腿平面上的复位力,N。

铅垂面上的复位力:

(5)

平均井斜狗腿平面上的复位力:

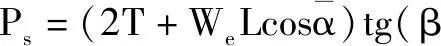
(6)

式中:β为平均井斜全角变化量,°。

平均井斜全角变化量:

β=arccos[cosα1cosα2+sinα1sinα2cos(φ1-φ2)]

(7)

式中:α1为下扶正器处井眼井斜角,°;α2为上扶正器处井眼井斜角,°;φ1为下扶正器处井眼方位角,°;φ2为上扶正器处井眼方位角,°。

扶正器安装间距长度井段对应的平均井眼井斜角:

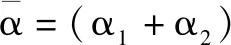
(8)

扶正器安装间距长度井段对应的井眼井斜角变化量:

Δα=α1-α2

(9)

扶正器安装间距长度井段对应的井眼方位角变化量:

Δφ=φ1-φ2

(10)

下扶正器处套管轴向力:

T=We(Hb-H)

(11)

式中:Hb为套管柱下入垂深,m;H为下套管扶正器处井眼深度,m。

在SY/T 5334—1996模型中认为套管内外的液体密度是相同的,从而忽略了液体密度差对居中度计算的影响。但是在现场的实际固井作业中套管内液体(即钻井液密度)与套管外液体(即水泥浆密度)是不相同的,为了更符合实际工况,改进了单位长度套管的浮重公式,单位长度套管在液体中的浮重:

(12)

式中:Wa为单位长度套管在空气中的重力,N/m;Dci为套管内径,cm;Dco为套管外径,cm;ρi为套管内液体密度(即钻井液密度),kg/m3;ρo为套管外液体密度(即水泥浆密度),kg/m3;ρs为套管钢材密度,kg/m3。

套管钢材弹性模量:

E=2.06×1011

(13)

式中：E为套管弹性模量，Pa。

套管横截面惯性矩:

(14)

式中：J为套管横截面惯性矩，m4。

1.2.2 刚性套管扶正器

相邻两只扶正器全为刚性扶正器时,套管最大偏心距:

emax=(Dh-Drc)/2+δ

(15)

式中:Dh为井眼外径,cm;Drc为刚性套管扶正器外径,cm。

相邻两只扶正器分别为刚性套管扶正器和弹性套管扶正器时,套管最大偏心距:

(16)

1.2.3 挠度公式

SY/T 5334—1996模型中的挠度公式考虑了铅垂平面上的复位力和狗腿平面上的复位力,在改进模型中考虑了套管径向力,采用了由Juvkam-Wold H C[18]根据弯曲变形理论[19]提出的套管最大挠度公式,即挠度公式改进为:

(17)

式中:F1为套管径向受力,N;μ为轴向载荷因数。

轴向载荷因数:

μ=(TL2/4EJ)0.5

(18)

套管径向受力:

(19)

式中:F1v为垂直于狗腿平面的径向受力,N;F1s为狗腿平面上的径向受力,N。

垂直于狗腿平面的径向受力:

F1v=WeLcosγo

(20)

cosγo=sinα1sinα2sin(φ2-φ1)/sinβ

(21)

式中:γo为重力方向与次法线的夹角,°。

狗腿平面上的径向受力:

(22)

(23)

式中:γn为重力方向与主法线的夹角,°。

2 模型比较

2.1 基础数据

使用C#语言将SY/T 5334—1996模型及本文的改进模型编写成程序,并采用实际案例比较两个模型及成像测井的平均套管居中度，同时探讨井斜角变化对结果的影响。

利用相储3井的数据对套管居中度进行分析,其中相储3井所用钻井液密度为1.47 g/cm3,水泥浆密度为1.7 g/cm3,密度差越大影响越明显[20]。井眼轨迹数据见表1,井身结构见表2,扶正器安放设计见表3。

表1 相储3井井眼轨迹数据表Tab.1 Well trajectory data of well Xiangchu 3

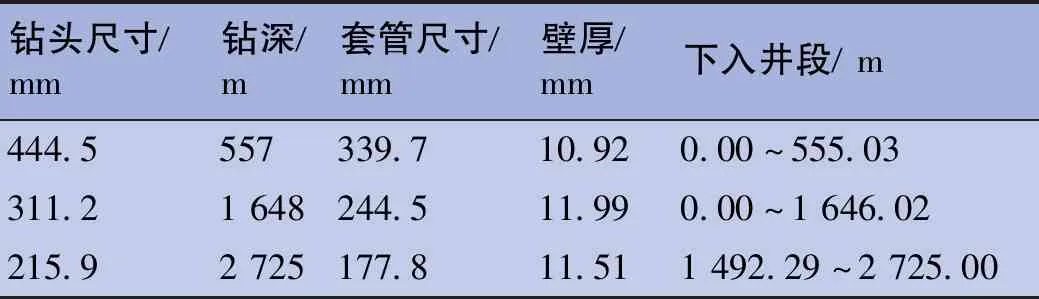
表2 相储3井井身结构数据表Tab.2 Data sheet of wellbore structure of well Xiangchu 3

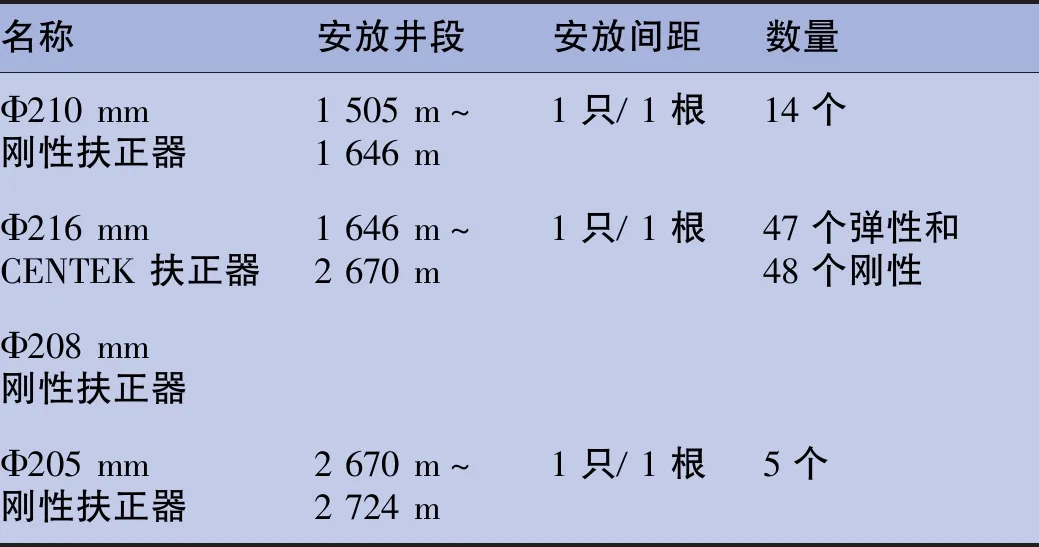
表3 相储3井扶正器安放设计表Tab.3 Design table for centralizer placement of well Xiangchu 3

2.2 结果比较

在相储3井的三开裸眼段(1 492～2 725 m)安放扶正器,进行居中度分析。该开次套管外径177.8 mm、壁厚11.51 mm、线重47.17 kg/m。现场作业中每一根套管安放一个扶正器,前段为Φ210 mm刚性扶正器,中间段为Φ216 mm弹性扶正器和Φ208 mm刚性扶正器混合安放,后段为Φ205 mm刚性扶正器。

比较成像测井数据及SY/T 5334—1996模型计算结果和在该模型基础上同时考虑套管内外液体密度差和新挠度公式及优化偏心距计算方法的改进模型计算结果,并参考了随井深变化的井斜角数据汇总成折线图,见图2。

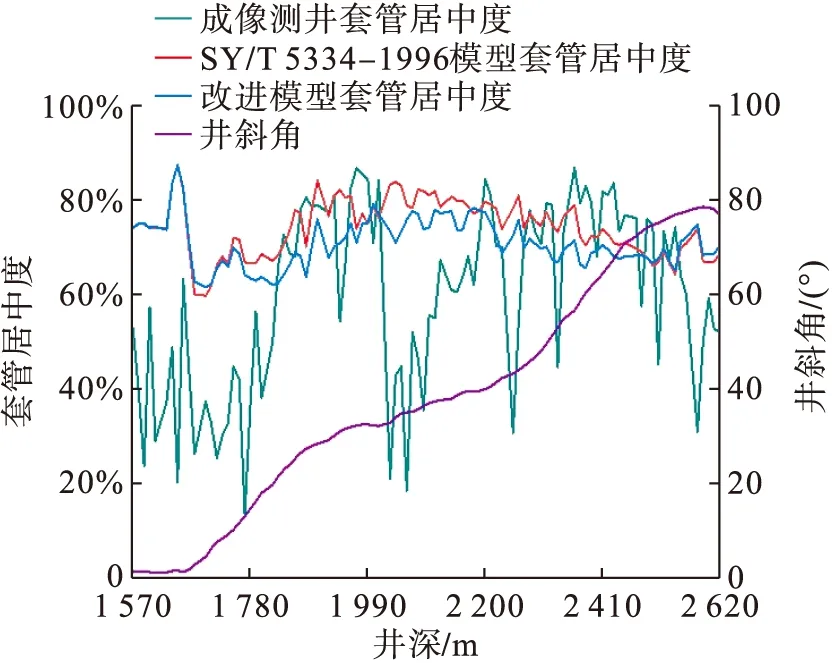
图2 相储3井套管居中度比较图Fig.2 Comparison of casing centering degree of well Xiangchu 3

由图2可知,用SY/T 5334—1996模型计算出的平均套管居中度是74.008%,而改进模型平均套管居中度为70.794%,SY/T 5334—1996模型所计算的平均套管居中度比改进模型平均套管居中度高3.214%。成像测井平均套管居中度是59.7%,SY/T 5334—1996模型平均套管居中度比成像测井数据高14.308%,改进模型平均套管居中度比成像测井数据高11.094%,所以改进模型所计算的平均套管居中度更接近现场实际情况。

为了更准确校核改进模型的准确度并探讨井斜角对居中度计算结果的影响,将三开井段平均分成5段,然后分段比较成像测井、SY/T 5334—1996模型及改进模型的平均套管居中度,见表4。

表4 相储3井平均套管居中度分段比较表Tab.4 Sectional comparison of average casing centering degree of well Xiangchu 3

由表4可知,改进模型的每一段平均套管居中度都比SY/T 5334—1996模型的平均套管居中度更接近成像测井的数据。其中1 570～1 770 m段和1 990～2 190 m段平均套管居中度偏大，与成像测井误差较大;1 780～1 980 m段和2 200～2 400 m段平均套管居中度非常接近于成像测井数据，误差很小。同时由图2可知,误差较小井段的井斜角为20°～30°及40°～80°,根据井眼轨迹可知这两段分别属于造斜段及水平段。