工业共生背景下供应链减排投资与定价的策略研究

侯贵生，孙颖异

(山东科技大学 经济管理学院，山东 青岛 266590)

一、引言

随着全球变暖的加剧，减少碳排放已成为所有国家的一项重要任务。[1]国家统计局显示，2021年1—7月我国粗钢累计产量6.5亿吨，与2020年同时期相比增长了8%，增加了约0.56亿吨产量，工业规模扩大使工业废弃物产生量逐年增加。2018年工信部发布《工业固体废物综合利用管理办法》，引导企业不断提高资源利用率，虽然我国工业固体废物的处理能力和规模有了显著提升，但其综合利用的提升空间依然很大，其中工业共生供应链以实现废弃物再利用为目标，这一创新理念逐渐被政府和各学者所重视。具体而言，以循环经济为理念的工业共生供应链意在整合不同类型产业，使某一产业的废弃物成为另一产业的原材料，依靠产业共生模式实现废弃物的利用化和减量化。

工业共生供应链是在生态工业园的基础上发展起来的，在经济相互独立的生产过程之间建立工业共生关系。[2，3]目前已有许多国家开展了工业共生项目。英国的国家工业共生计划(National Industrial Symbiosis Programme,NISP)为企业提供了可利用废弃物，企业实现减排的同时获得巨大利润。[4，5]开普敦于2013年启动的西开普工业共生项目，在过去五年中，共减少废弃物排放27 400吨，完成了46 700吨的碳减排。Bansal[6]以加拿大安大略省的企业为例，研究工业共生供应链与传统供应链之间的区别，认为企业可以从副产品中获得巨大价值。我国辽宁、山东、河北和天津等地也已开展了生态工业园区试点项目。[7]

一些学者对工业共生的概念[8]、影响因素[9]等进行了研究，大多数学者基于特定案例[10]对工业共生展开分析，如Ohnishi[11]运用物质流分析法对日本川崎生态城镇的经济和环境问题进行了定量分析，Eckelman等[12]运用生命周期法分析了美国檀香山坎贝尔工业园区运行模式的环境成本和收益，Jung等[13]运用现金流贴现法评价了韩国生态工业园区的经济和生态效益。上述学者多侧重研究特定区域内的工业共生模式，缺乏一定的普适性，缺少对工业共生体系内不同企业的最优决策和效益的分析。基于此，许多学者将工业共生模式与数理模型相结合，进一步分析工业共生供应链的经济和环境效益，如Zhang[14]采用模糊目标规划方法构建共生网络优化模型，通过投入产出矩阵识别共生网络中企业的碳足迹，进而在产品需求和减排成本约束下建立优化模型。Yan[15]等将ABM(agent-based model)模型与非合作博弈相结合，用来协定工业共生中额外的成本分摊。Lou[16]运用非合作博弈理论方法，探寻工业共生模式下经济和环境效益达到最优状态的平衡条件，但各参与者均以个人利益最大化为准则，没有达到整个系统的最佳状态。Andiappan[17]借助合作博弈模型对工业园区企业的利益进行合理分配，同时考虑联盟的稳定性和鲁棒性。Tan[18]建了线性规划合作博弈模型，解决了生态工业园参与者的利益分配问题。上述文献将工业共生模式与博弈理论相结合，探寻企业最优经济和环境绩效，同时考虑了共生模式内企业的收益分配问题，但忽视了政府规制和消费者环境偏好对废弃物交易价格和利用量的影响。

在以市场为导向的经济体制下，企业以经济利益为首要目标，高污染企业在面对巨额减排成本时，往往会选择排放废弃物来优先实现其经济目标，因此政府规制在工业共生供应链的初期发展阶段显得尤为重要，其中碳交易政策作为控排最有效的市场机制，出现在众多工业共生研究中。如Zhao[19]在碳税和碳交易政策下，建立上下游制造商的进化博弈模型，认为环境规制是推动工业共生的驱动力，碳交易机制为减排投资活动提供了新的融资渠道，可连接物质流与现金流，有利于实施低碳生产。肖忠东[20]建立了政府与废弃物供需方的演化博弈模型，研究表明与排放权交易搭配的混合式环境规制能推动上下游企业形成工业共生关系，企业可以签订契约分配减排成本和减排收益。上述文献将工业共生模式与博弈论相结合，同时探讨排放权交易政策对废弃物利用的影响，认为排放权交易可以推动工业共生关系的形成，这为本文研究排放权交易对共生链的影响奠定了基础，但没有考虑到消费者环境偏好的影响。Shan[21]构建了工业共生模式下生产者、分解者和消费者的博弈模型，但没有考虑排放权交易。

随着低碳经济和碳中和等理念愈演愈热，消费者对产品的环保特性更加重视，并愿意花高价购买环保型产品。[22]Zhu[23]根据消费者对产品环保特性的反应程度，将消费者分为三类，当环保型消费者比例高或消费者对环保产品的欣赏度更高时，企业更愿意实行工业共生模式。基于此，本文研究工业共生模式下废弃物利用和产品定价策略时，产品定价不仅关注上游废弃物交易价格，更着重研究制造商最终产品价格，这主要在于制造商关于终端产品的定价会影响上游废弃物的循环利用量。Tang[24]研究了工业共生模式下最优定价和产量决策问题，认为废弃物供需关系受消费者价格敏感度的影响，当消费者对价格较为敏感且制造商原材料成本较高时，更有利于建立工业共生模式。Cao[25]分析了工业共生链中废弃物排放水平和定价的联合决策问题，引入消费者价格—环境敏感需求，消费者较强的绿色环保意识能迫使制造商降低废物排放水平。He[26]基于产业园区企业构建立了废弃物回收定价模型，旨在完善废弃物回收价格机制，其中终端市场需求受消费者价格敏感度的影响，但却没有考虑制造商减排投资行为。在政府环境规制、消费者环境偏好等多重因素驱动下，制造商作为碳排放主体，会选择减排投资等策略来解决生产经营造成的环境危害，这势必会影响其成本结构和定价，进而对上游废弃物交易产生影响。

因此，本文建立排放权交易政策下废弃物供应商和制造商组成的集中式和分散式决策模型，求解双方最优决策变量，最后通过两部定价契约机制协调链内企业收益，分析排放权交易价格、消费者偏好以及减排投资行为对供应链废弃物利用和产品定价的影响，以及各参数变化对供应链效益的影响，以期为企业决策和政府政策制定提供理论基础。与现有研究相比，本文创新点如下：首先，将工业共生模式与博弈理论相结合，从供应链的决策理念出发分析工业共生废弃物的利用化和减量化问题，丰富拓展了生态工业园的研究；其次，与以往研究不同，本文考虑了排放权交易和消费者偏好对工业共生模式构建的影响，对工业共生模式的外部影响因素进行更全面的分析；最后，本文引入了制造商投资减排行为，在碳规制和消费者偏好作用下，研究企业减排投资对废弃物交易决策的影响，使工业共生模型更具现实意义。

二、模型描述与假设

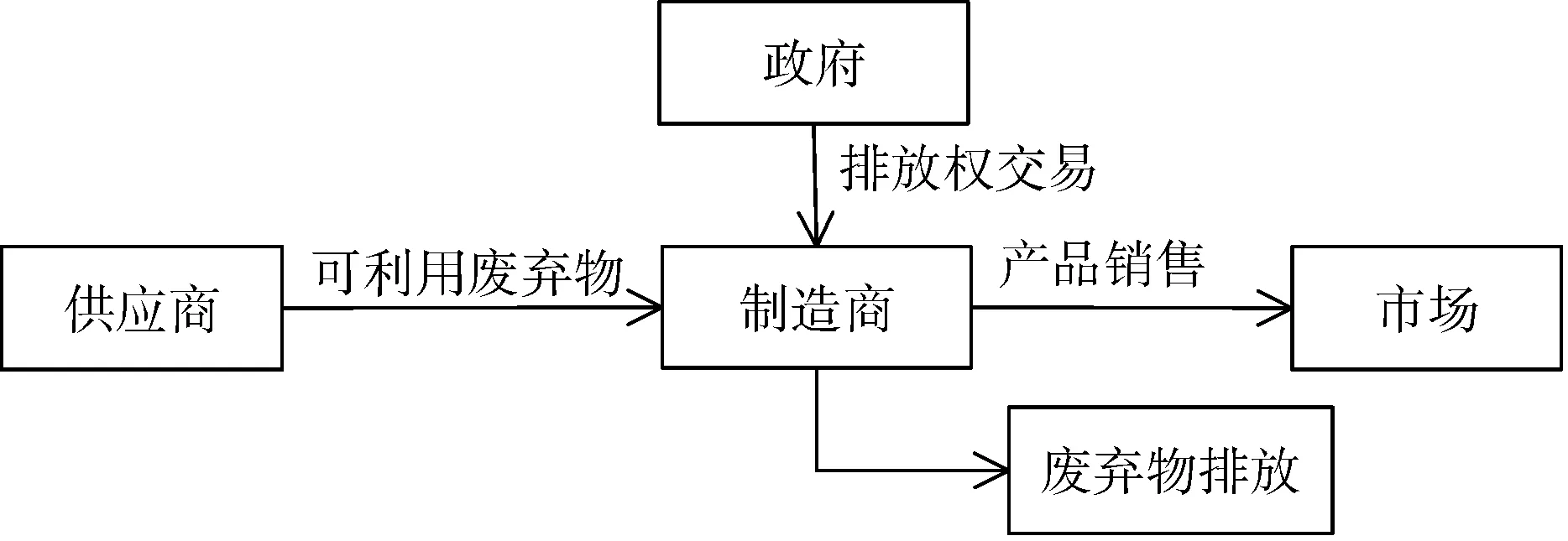
图1 排放权交易下工业共生供应链结构模式

模型假设：

(1)为保证产品价格和市场需求的非负性，相关参数满足a-α(cm+cs+pce0)>0。

(3)根据贺勇，陈晓红等的研究，[30，31]考虑到市场需求受产品价格和单位减排量的影响，产品需求函数为D=a-apm+βem，其中a为产品的潜在市场需求，α为单位价格造成的市场需求减少量，β为单位减排引起的市场需求增加量。本文重点考虑环境规制和减排投资对工业共生供应链的影响，因此假设产品需求与废弃物供应量相等，供应商的供给满足制造商的产品需求，并且为了方便后续模型的求解和分析，一单位产品需要一单位的可循环废弃物。

在下列各模型中，下标s、m分别代表废弃物供应商和制造商的相关变量，下标ni为供应链不减排投资情形，上标d、c和t分别代表分散式决策、集中式决策和两部定价契约下的相关变量，公式上标*为最优决策变量表达式。

基于以上假设，本文建立废弃物供应商和制造商组成的工业共生供应链模型，研究排放权交易政策和消费者环境偏好对工业共生关系构建的影响，以及不同决策模式下制造商有无减排投资对供应链收益和环境的影响，比较了减排投资前后供应链废弃物利用量、减排量和产品价格等因素的变化，最后设计契约使供应链整体达到最优利润，协调各方收益。

三、排放权交易政策下供应链不减排投资的模型分析

(一)分散式决策下的模型分析

当供应链不投资减排时，即在排放权交易无减排投资的情况下em=0，废弃物供应商和制造商的收益函数分别为：

(1)

(2)

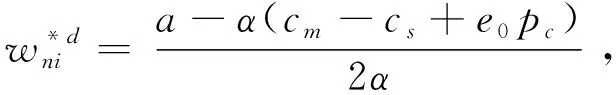
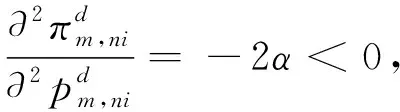
(3)

(4)

再将公式(4)代入到公式(3)，得最优产品价格为：

(5)

(二)集中式决策下的模型分析

集中决策是一种典型的供应链管理策略，诸多学者在利用博弈理论探讨供应链问题时用到集中式决策进行分析和研究，集中式决策弱化了分散式决策的“双重边际”现象，协调链内企业间的行为，使各成员作为一个整体统一决定最优产品价格，实现供应链整体最优利润[32]。

无减排投资情况下供应链整体利润函数为：

(6)

(7)

通过计算无减排投资下的两种决策模式，得到废弃物交易价格、减排量、产品价格和利润等变量表达式，发现集中式决策下产品价格更低、市场需求更多、总利润更大，所以当制造商不减排投资时，集中式决策更优。

四、排放权交易政策下供应链减排投资的模型分析

(一)分散式决策的模型分析

供应商和制造商的利润函数为：

(8)

(9)

(10)

所以4α(i-βpc)-(β-αpc)2>0，4αi-(β+αpc)2>0，符合约束条件。

(11)

(12)

将公式(12)代入到公式(11)中，可得最优产品价格和减排量为：

(13)

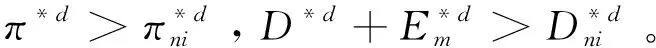
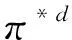
综上，分散式决策下，排放权交易减排投资下的经济效益和环境效益均大于排放权交易无减排投资下的利润和废弃物利用量，其中经济效益指的是供应链整体经济利润，环境效益指的是可循环废弃物利用量和制造商废弃物减排量。

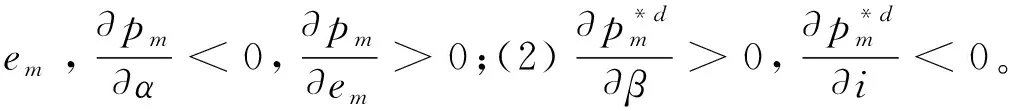
(二)集中式决策下的模型分析

已有学者指出，虽然分散式和集中式决策下碳排放量的变化趋势相同，但集中式决策下的碳排放低于分散式决策，并且集中式决策下制造商碳排放的划分标准也更低，[32]因此进一步考虑减排投资下的集中式决策模型。

供应链利润函数为：

(14)

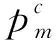
(15)

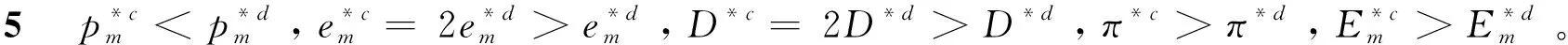
通过比较减排投资时的两种决策模式，发现集中式决策下产品价格更低、市场需求更多、总利润更大，制造商的减排效果明显优于分散决策，即相同投资成本下，制造商的最优减排量更多，因此集中式决策更优。而分散式决策下，随着市场需求的上升，制造商的订购成本、减排成本和排放权交易成本都会增加，同时产品价格下降，势必会影响制造商的利润，因此需要通过契约机制协调双方需求，实现供应链整体利润最优的局面。

(三)两部定价契约

两部定价契约下，供应商以价格wt向制造商出售可循环废弃物，同时向制造商收取一定的费用F。供应商和制造商的收益函数分别为：

(16)

(17)

(18)

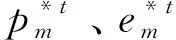
综上，定理5表明两部定价契约下制造商的最优产品价格和废弃物减排量与集中式决策下的相等，供应商废弃物交易价格等于其加工处理成本，接下来讨论该契约履行的条件。

定理6当固定费用F满足以下条件时，两部定价契约可以实现共生供应链协调。

(19)

五、算例分析

本文用matlab2017a进行数值分析，更直观地展示有无减排投资时分散式和集中式决策下各变量的大小关系，进一步探究消费者偏好敏感系数、排放权交易价格和投资减排成本系数对供应链决策变量和收益等的影响。

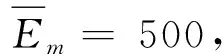
(一)消费者价格敏感系数的影响分析

如图2所示，制造商不减排投资情形下，随着消费者价格敏感系数的增加，两种决策模式下废弃物总排放量降低，原因是消费者价格敏感系数上升导致产品需求下降，制造商产量下降，产生的废弃物也有所减少。减排投资情形下，制造商废弃物总排放量随着价格敏感系数的增加而增加，当消费者更偏好价格低廉的产品时，制造商为了顺应市场需求，降低废弃物减排投入，压缩产品生产成本，因此废弃物排放增多，但两种决策模式下的废弃物排放仍少于不减排投资的情形。不减排投资情形下，集中式决策的废弃物排放总量远远大于分散式决策，因为集中式决策的市场需求更多，废弃物排放也多，相比之下，在一定的价格偏好系数范围内，减排投资集中式决策的排放总量低于分散式决策，即减排投资集中式决策可以实现更好的环境绩效。

图2 消费者价格敏感系数对排放量的影响

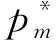
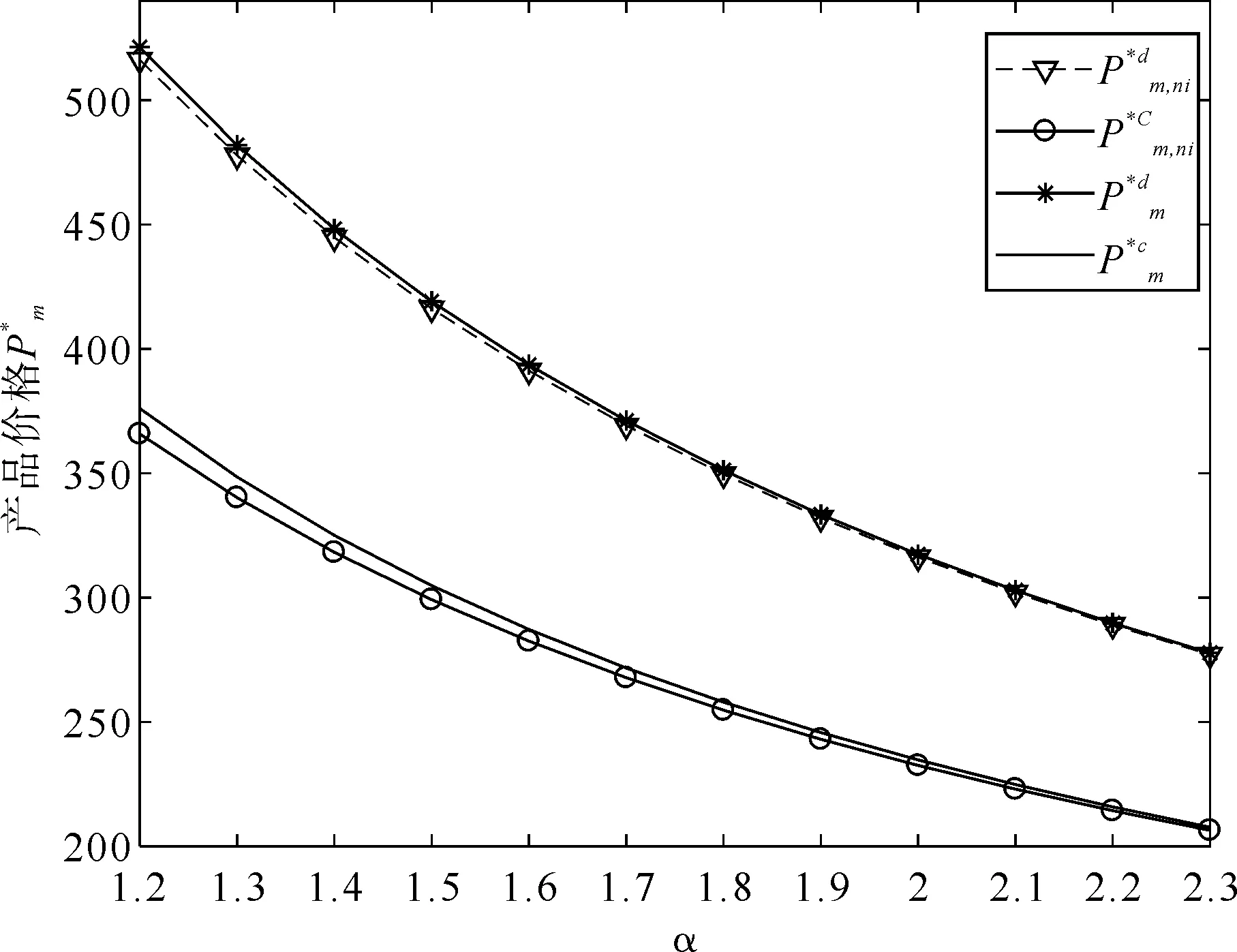
图3 消费者价格敏感系数对产品价格的影响

如图4所示，随着价格敏感系数的增加，四种情形下的市场需求均呈下降趋势，消费者对产品价格敏感导致市场需求下降。不难看出集中决策下的市场需求均大于分散式决策，因为集中式决策下制造商有更多的降价空间，可通过降价获取更多市场份额，其中减排投资集中式决策的市场需求最大，不减排投资分散式决策的产品需求最小。

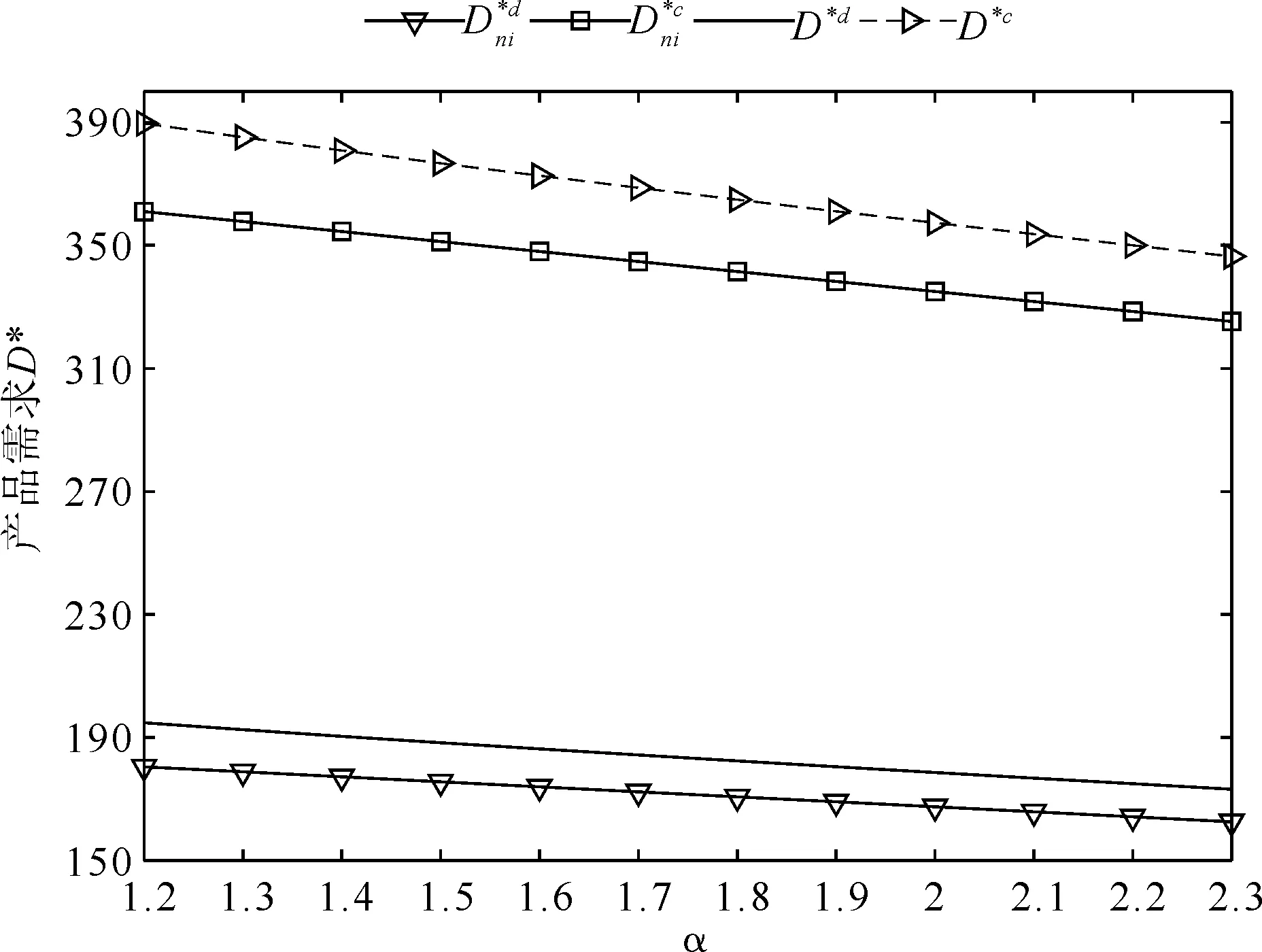
图4 消费者价格敏感系数对产品需求的影响

如图5所示，随着价格敏感系数的增加，双方利润都呈下降态势，因为消费者对价格的敏感度上升，制造商降价进而压缩了一部分利润，但减排投资分散式决策下双方利润均大于不减排投资，即虽然消费者价格敏感度上升，但制造商减排量的增加使减排投资下的市场需求大于不减排投资情形下的市场需求。因此减排投资可以有效增加共生链的环境效益和经济效益，证明了本文引入制造商减排投资行为的合理性。

图5 消费者价格敏感系数对上下游企业利润的影响

(二)排放权交易价格的影响分析

图6 排放权交易价格对上下游企业利润的影响

减排投资集中式决策下共生链整体利润远远大于分散式决策，因此有必要建立契约机制实现上下游企业合作，从而使工业共生链获得更高水平的经济效益。减排投资集中式决策下废弃物排放量随着排放权交易价格的增长急剧减少，考虑排放权交易价格的上升使制造商获得更多额外收益，促进了制造商减排，因此减排投资集中式决策模型对环境的改善效果最大，论证了本文研究集中式决策和减排投资行为的科学性，具体见图7。

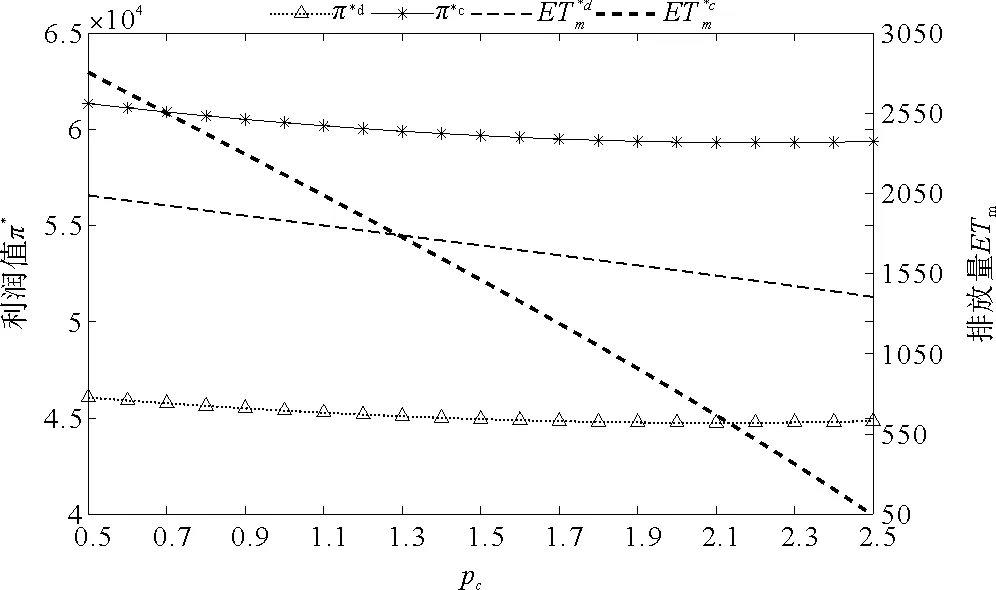
图7 排放权交易价格对供应链利润、排放量及减排水平的影响

图8 排放权交易价格与产品价格的关系

如图9所示，不减排投资情形下，产品需求随着排放权交易价格的增加而线性下降，因为pc上升导致产品价格提高，进而市场需求下降，这里市场需求也为上游可循环废弃物利用量。但减排投资情形下，市场需求随pc的上升而不断增加，因为排放权交易价格上升引起产品价格下降，市场需求增加，所以排放权交易价格的上升不仅可以减少制造商排放，还会增加上游可循环废弃物的使用量，减少环境危害的同时促进资源有效利用。

图9 排放权交易价格对产品需求的影响

图10 不同决策模式下排放限额与交易价格对排放权交易量的影响

当排放权交易价格小于一定范围时，集中式决策的排放权交易量小于分散式决策，反之，则大于分散式决策，因此与分散式决策相比，集中式决策在排放权交易价格上升时能出售更多的排放权，实现更多减排量。

(三)减排投资成本系数的影响分析

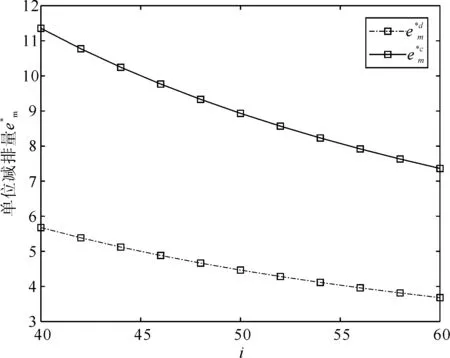
图11 减排投资成本系数对单位减排水平的影响

减排投资成本系数不断增加，单位减排量需要投入更多成本，两种决策下的排放量都呈增加趋势，双方利润有所下降。如图12所示，当i小于等于45时，集中式决策的排放量小于分散式决策，当i大于45时，集中式决策的排放量大于分散式决策，因为减排难度变大，而集中式决策的市场需求更多，制造商生产量增多，因此排放量也增多。

图12 减排投资成本系数对利润和废弃物排放量的影响

六、结论

本文在工业共生背景下，构建了废弃物供应商和制造商组成的工业共生供应链模型，研究了排放权交易下有无减排投资的集中式决策和分散式决策模型，并进行两部定价契约设计，分析了消费者偏好、排放权交易政策和减排投资对供应链各方最优决策变量和利润的影响，通过研究得出以下结论。

1.在政府规制和消费者环境意识并存的当下，工业共生供应链中制造商减排投资不仅减少了自身碳排放，还提高了上游可循环废弃物的利用量，减少了工业废弃物的排放污染，提高了供应链整体利润。同时在减排投资情形下，各参与方通过两部定价契约实现了与集中式决策相同的效益。

2.不减排投资情形下，集中式决策的废弃物排放总量远大于分散式决策，而减排投资情形下，在一定的消费者价格偏好系数范围内，集中式决策的排放总量更低，即减排投资集中式决策可以实现更好的环境绩效；随着排放权交易价格的上升，不减排投资时双方利润均呈下降态势，减排投资时制造商的利润随排放权交易价格的增加而不断增长，同时废弃物供应商的利润下降幅度与不减排投资相比明显变小；不减排投资情形下，排放权交易价格与产品价格呈正比，减排投资下，随着排放权交易价格上升，制造商越具有价格竞争优势；不减排投资情形下，产品需求随排放权交易价格的增加而线性下降，减排投资下，市场需求随排放权交易价格的上升而不断增加，同时上游可循环废弃物利用量也不断增加。

3.减排投资成本系数越低，双方收益越多，排放量越小。当减排投资成本系数大于某一阈值时，集中式决策下的排放量大于分散式决策。同时固定限额下，排放权交易价格越高，制造商越愿意减排投资；当pc不变时，排放限额越大，制造商越愿意减排投资。本文研究认为废弃物排放限额过低，将影响企业正常生产经营，限额过高又容易对环境造成负担，助长工业污染，因此政府要根据企业成本设置合理的限额，与排放权交易机制一同引导企业减排投资。

本文仅考虑了单个上下游企业，但现实中存在多个可循环废弃物供应商与多个制造商交易的情况，相互之间的竞争关系会对工业共生模式产生新的作用。同时下游制造商对可循环废弃物的需求受产品市场的影响，废弃物供需关系不确定，因此，未来研究应考虑企业间的竞争性和废弃物供需关系。