建筑结构风压与蓄滞洪区风速计算方法研究

潘晓春，石 军，程春龙，王晓惠，沈旭伟

(中国能源建设集团江苏省电力设计院有限公司，江苏 南京 211102)

0 引言

大风荷载是各类工程特别是高、大、细、长等柔性结构的主要设计荷载。风灾是造成结构损伤甚至破坏的重要原因，风荷载计算的合理和全面与否是工程抗风设计和抗风防灾安全的重要因素[1]。

蓄滞洪区主要指洪水临时贮存的低洼地区及湖泊等。蓄滞洪区洪水淹没时间长，汛期滞洪历时可达数月，长时间滞洪势必增加遭遇大风的可能性，此时处在洪水中的房屋等建(构)筑物就要受到波浪荷载作用。波浪对建(构)筑物的作用主要表现在波浪的动水压力。计算表明，在6～9级风浪情况下，作用在普通房屋墙面上的波浪动水压力最大可达到3～10 kN/m2。 在这样大的荷载作用下，一般房屋是难以承受的。因此，滞蓄洪期间对房屋危害最大的当属波浪荷载[2-3]；此外，蓄滞洪区内的近水面安全层楼、屋盖板底面的设计标高确定时也需要设计风浪高度。我国标准[4]采用由设计风速推算设计风浪要素的方法，因此需先行计算确定蓄滞洪区设计风速。

然而，我国现行国家标准[4-5]在建筑结构设计风压和蓄滞洪区计算风速(设计风速)分析计算方面均存在一些瑕疵或问题，为准确确定结构风荷载与蓄滞洪区波浪荷载，本文对相关条文提出修订建议。

1 《规范》中重现期风压换算存在的问题

现行GB 50009—2012《建筑结构荷载规范》(以下简称《规范》)第E.3.1条、E.3.3条均假定“雪压”和“风速”的年最大值均服从极值I型概率分布，两者的重现期设计值均可通过极值 I型分布的样本统计参数确定。然而第E.3.4条中，“雪压”没变，“风速”却替换成了“风压”，即其他重现期的“雪压”和“风压”均要求按同一公式即式(E.3.4)换算。

那么，像第E.3.4条那样“风速”直接替换为“风压”在理论上是否正确，或年最大风速与风压是否属于同一种概率分布，证明如下：

设随机变量X具有密度函数f(x)；随机变量Y=φ(X)，以g(y)表示Y的密度函数。设以B表示某一取值集合，并以AB表示集合 ｛x; φ(x)∈B｝，则有：

若y=φ(x)在定义域内对任意y值具有唯一解，即φ(x)为单调函数。对式(1)进行积分变量代换x=φ-1(y)，可得：

其 中，J(y)=dx/dy=d[φ-1(y)]/dy为 雅 可 比(Jacobi)式[6]。对比式(2)，有：

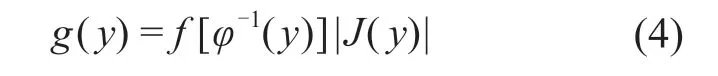
当φ(X)为X的线性函数时，由于J(y)为常数项，g(y)与f(x)属于同类分布，只是曲线的起点(位置参数)发生系统性平移。而当φ(X)为X的非线性变换时，由于J(y)是y的函数，即所得g(y)与f(x)属于不同类型分布。

作为风速的2次幂指函数的风压，与风速不属于同一类型的概率分布，亦即若假定年最大风速服从极值I型分布，则相应风压不服从该分布。因此，基于年最大风速服从按极值 I型分布的假定《规范》采用式(E.3.4)进行不同重现期风压换算在理论上是不严谨的。

2 重现期风压的插值计算法

2.1 插值计算公式推导

假定年最大风速服从极值I型分布，分布函数为[5]：

式中：u为风速概率分布的位置参数，即分布的众数；α为风速概率分布的尺度参数。

重现期为R的最大风速vR按下式计算[5]：

根据伯努利方程，风压wR与风速符合下式：

式中：ρ为空气密度。

则式(6)整理为：

将重现期R分别取10 a、100 a时的风压值w10和w100分别代入式(8)，联解u、α，整理得重现期为R的最大风压wR计算式，得：

对数函数的Taylor展开[7]为：

当｜x｜足够小或R足够大，忽略高阶项，有：

若假定风压服从极值I型分布，即重现期风压按式(13)计算：

式中：u'为风压概率分布的位置参数；α'为风压概率分布的尺度参数。

对式(13)进一步按式(10)取近似，即：

对比可见，式(15)正是《规范》的式(E.3.4)。从2001版开始，《规范》就采用该式内插各重现期风压[5，8-9]。

2.2 插值计算公式精度评价

由前文推导过程可知，《规范》的式(E.3.4)隐含了2项近似，即：①年最大风速服从极值 I型分布，风压也服从该分布；②对数函数取其Taylor近似。

式(9)、式(12)以及式(15)均采用w10和w100内插其他重现期的风压wR，而《规范》表E.5同时也提供了全国代表气象站的w50。下面分别采用上述3个公式计算w50，并将计算结果与《规范》表E.5中的w50进行对比，用于评价各计算式的精度。

由于《规范》表E.5中的风压基本单位为0.05 kN/m2，若风压过小，计算误差可能被此种幅度的单位掩盖，因此选取风压值较大的东南沿海12座气象站和新疆4座气象站风压计算评价。w50计算结果及误差统计分别见表1～表2所列。

表1 东南沿海和新疆16座代表性气象站50 a一遇风压计算结果表kN/m2

表2 东南沿海和新疆16座代表性气象站 50 a一遇风压计算误差统计

续表

由表2误差统计成果可见：

1)式(15)计算相对误差明显高于式(9)和式(12)，这反映了风压与风速同样服从极值 I型分布假定可能带来相对显著的误差。

2)式(9)与式(12)的计算误差相当接近，说明了采用式(10)对数函数的Taylor近似在计算精度方面令人满意。

3)理论上式(9)精度最高，但由于《规范》表E.5中的风压基本单位为0.05 kN/m2，式(9)在精度上的优势难以显现。

综上，式(9)、式(12)均可作为内插重现期风压的可靠计算公式，而式(15)即《规范》中的式(E.3.4)则可能带来一定的误差，这在设计风压或设计风速较大的地区尤为明显。

进一步地，还可以视所求风压的重现期R大于50 a还是小于50 a，仿照前文推导过程，并取对数函数的Taylor近似，得出更精确计算重现期为R的最大风压wR。即：

当R＜50 a时：

3 《标准》中计算风速存在的问题

现行GB/T 50181—2018《洪泛区和蓄滞洪区建筑工程技术标准》(以下简称《标准》)第A.0.3条规定，对缺乏实测风速资料地区的设计风浪计算需要的计算风速，可通过当地基本风压和风速变异系数(也称“离差系数”)等来计算，当地基本风压可由建筑结构荷载查得。然而，《标准》在计算风速方面存在如下主要问题。

1) GBJ 9—87《建筑结构荷载规范》采用的基本风压重现期为30 a[10]，因而《标准》的1993版基于此，经理论推导提出由基本风压推算蓄滞洪区风浪计算风速的方法[11]，这些在当时的两部国标之间是一致的。从《规范》2001版开始直到现行2012版，我国基本风压的重现期早已由30 a提升为50 a，各地基本风压的数值也多有变化[4，11-12]。然而，《标准》 第A.0.3条第3～4款仍然照搬其早前的版本，未针对基本风压重现期等变化重新拟定公式和 系数。

2)《标准》基于全国气象站推算并推荐采用统一的风速变异系数0.151，未针对我国各流域蓄滞洪区所在地域的不同风速变异系数分别拟定相关计算式。此问题始见于1993版直至现行版本[4，11-12]。

4 蓄滞洪区最大风速变异系数推算

4.1 我国蓄滞洪区和洪泛区的地域分布

《标准》里设计风浪的计算风速应针对蓄滞洪区和洪泛区。我国各流域设置的蓄滞洪区已由97处调整为94处，各流域蓄滞洪区数量见表3所列[13-15]。

表3 我国各流域防洪规划调整后的蓄滞洪区数量

全国蓄滞洪区面积比例分布、蓄洪容积比例分布分别如图1～图2所示[13]。

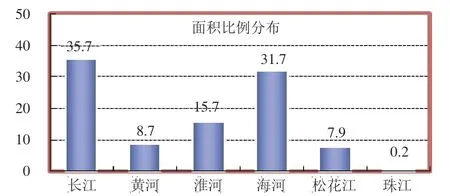
图1 全国蓄滞洪区面积比例分布图

图2 全国蓄滞洪区蓄洪容积比例分布图

从蓄滞洪区数量、面积、容积来看，均以长江流域为最，海河流域次之，淮河流域第三，黄河流域与松花江流域大致相当。洪泛区一般位于流域的中下游，可以在蓄滞洪区的基础上适当扩大范围。

蓄滞洪区和洪泛区里风浪的计算风速应重点针对上述地域分布特点，即最大风速的研究范围应有所侧重，而不是现行国标里的基于“全国各地风速进行统计分析”。

4.2 蓄滞洪区最大风速变异系数推算

极值I型分布有限样本的变异系数与样本长度有关，从而推算变异系数时需要预知样本长度[5-6]。根据《规范》第8.1.2条所述，目前我国各地基本风压依据的样本大致为 1960—2008年，长度约49 a。

《规范》附表E.5列出了全国约590座气象站重现期分别为10 a、50 a和100 a的设计风压值，从中筛选出位于六大流域蓄滞洪区和洪泛区范围及其附近的气象站共112座。利用这些气象站的上述3种重现期设计风压反推各站年最大风速变异系数。

基于变异系数，设计风速标准化计算式：

式中：vR为重现期为R的设计风速；为年最大风速均值；S为年最大风速均方差；δv为年最大风速变异系数；λR,n为样本长度为n、重现期为R的极值I型分布的离均系数，其值可编程计算或查参考文献[16]表D.0.2。

考虑到式(7)，式(18)改写为：

式中：wR为重现期R的设计风压。

若已知两个重现期的设计风压值wR1、wR2，分别代入上式导出：

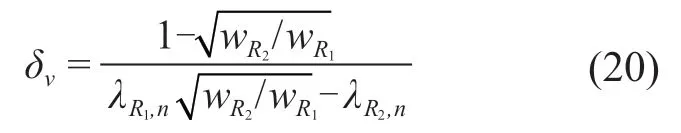
将重现期分别为10 a、50 a和100 a的设计风压值两两代入式(20)计算，可得3个δv计算值。由于《规范》附表E.5列出的风压值的基本单位为0.05 kN/m2，存在“四不舍五必入”的取整误差，因此许多气象站这3个δv计算值并不完全相同，见表4所列。本文取三者平均进行如下分析。

基于表4所列112座气象站最大风速δv值，绘制我国蓄滞洪区最大风速等值线如图3所示，其中局部地区如图4所示。

图4 长江流域蓄滞洪区风速变异系数等值线

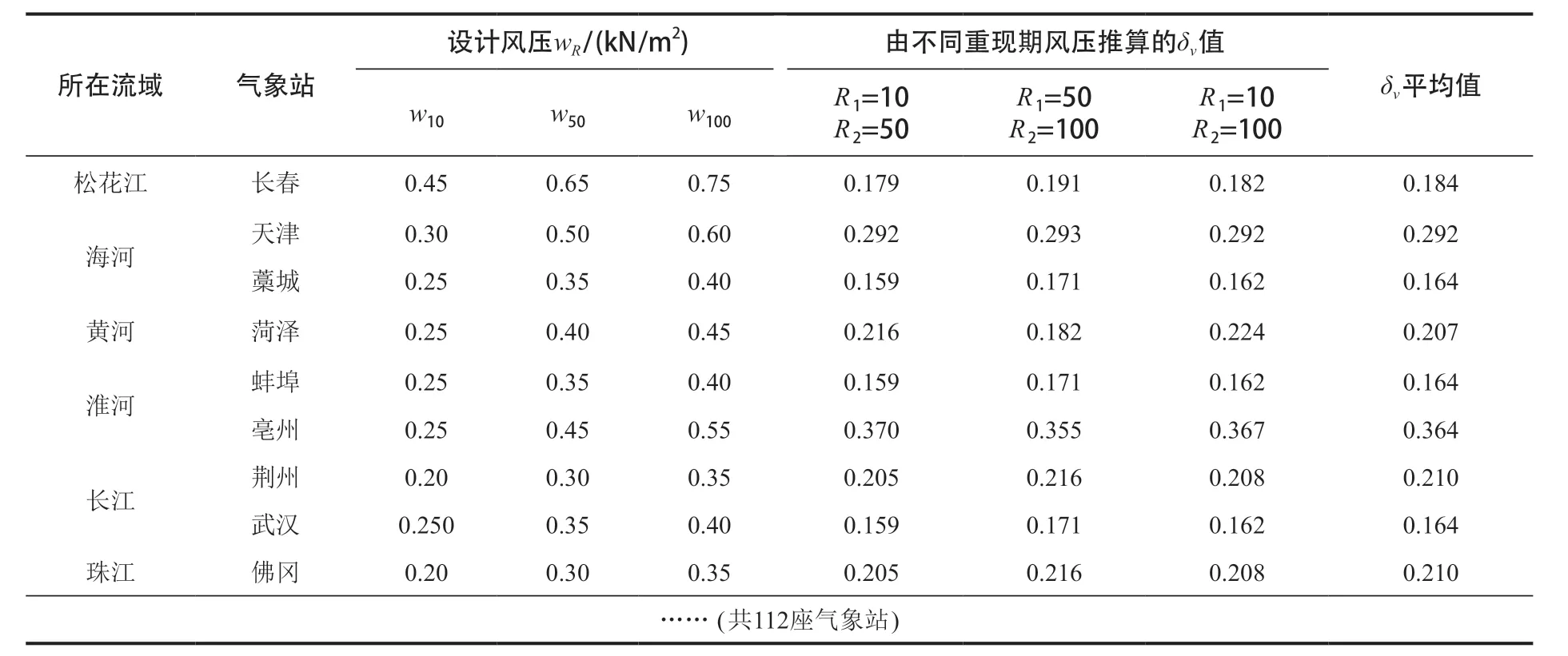
表4 代表性气象站风速变异系数计算值

图3 我国蓄滞洪区风速变异系数等值线

基于图3～图4所示风速变异系数及各流域蓄滞洪区位置等，对我国94处蓄洪区最大风速系数分0.29、0.25、0.21及0.17共4档适当归并，成果见表5所列。

表5 我国蓄滞洪区风速变异系数建议取值

对缺乏实测风速资料的蓄滞洪区的年最大风速变异系数可按上表近似取值；对具有20 a以上风速资料计算的变异系数也应据此进行合理性检查；洪泛区可就近参照表5取值。

5 由风压推算蓄滞洪区计算风速

5.1 蓄滞洪区设计风速与基本风压的一般关系

现行《规范》给出的基本风压为50 a一遇，系按年最大风速数据统计而得，并非蓄滞洪区期间的风速。基于荷载规范的风压值确定蓄滞洪区期间的最大风速的方法，推导如下。

设Twa一遇的最大风速为vw，则：

由两种相互独立的活荷载的相遇概率，导出蓄滞洪区两次运行时间间隔T1与计算风速重现期Tw的关系[5]：

将式(25)代入式(24)，并考虑基本风压w0与基本风速v0之关系，从而有：

5.2 蓄滞洪区设计风速与基本风压的简化关系

极值I型分布参数u、α符合下式[5]：

式中：C1,n、C2,n为与样本长度n有关的系数，其值可编程计算或查参考文献[5]表E.3.2。

由式(18)，重现期50 a的基本风速符合下式：

将 λR=50,n=49=2.894，C1,n=49=1.15901，C2,n=49=0.54812和δv值代入上式即可计算u/v0值。

1)当δv=0.29时，各 系 数 代 入 式(29)有 u/v0=0.4692，将其代入式(26)，则：

《规范》第A.0.3条第4款变相限定了T1的实际范围为[5，15]。在此范围内，的关系近乎线性，回归式为：

2)当δv分别为0.25、0.21、0.17时，同理分别导出式(33)～式(35)：

当δv=0.25时：

由此可见，当基本风压值重现期由30 a变为50 a后，u/v0值已非《标准》条文说明式(19)给出的0.7。由此导出的蓄滞洪区不同重现期计算风速的关系式也非《标准》中的式(A.0.3-5)，即式(36)：

我国蓄滞洪区风速变异系数、设计风速与基本风压的关系汇总见表6所列。洪泛区按照地区相邻原则选择表中系数与公式。

表6 我国蓄滞洪区设计风速与基本风压的关系式

6 结论

1)技术标准体系之间应相互协调，标准修编时应密切关注引用或指向的其他标准的相关变化，采用最新最合理的方法修订标准；同时应准确把握条文针对的具体对象，关注相关问题的时空分布规律，从基本理论入手提出合理的分析计算方法，以正确指导工程建设。

2)若假定年最大风速服从极值I型分布，却又认为风压也服从该分布，这在理论上是不严谨的，也是导致现行《规范》重现期的风压换算的式(E.3.4)，即本文式(15)的计算精度偏低的主要原因。

3)设计风压较大的地区、海上风电工程中的不同重现期的风压换算，以及输电线路工程基于风压图换算设计风速进行分区取值的临界点等方面，均需要采用精度更高的重现期风压换算式。本文建议《规范》修编时采用式(9)或相对简洁的式(12)进行重现期风压换算，若要获取更高的精度，还可采用分区间的式(16)、式(17)。不同重现期的风压换算仍可采用《规范》式(E.3.4)。

4)我国基本风压的重现期早已由30 a提升为50 a。基于现行《规范》的蓄滞洪区年最大风速变异系数依不同流域呈现不同的值，不宜按现行《标准》第A.0.3条第3款推荐采用的仅0.151一个固定值，设计风速与基本风压的关系也并非《标准》式(A.0.3-5)。建议《标准》修订时参考本文表5～表6给出的各蓄滞洪区最大风速变异系数以及设计风速与基本风压的计算关系，修订相关条文及其说明。

5)从上下文符号含义来看，《标准》条文说明式(16)和式(17)符号存在排版错误：“2”应为尺度参数“α”“δv”应为均方差“σv”；《标准》条文说明式(12)、式(14)还应如《规范》第E.3.2条考虑有限样本下的参数估计。