Z型钢板桩码头转角段三维数值模拟

2022-11-01郭浩霖李春阳王志斌

水运工程 2022年10期

郭浩霖，李春阳，王志斌

(中交第四航务工程勘察设计院有限公司，广东广州 510290)

板桩码头具有结构简单、对复杂的地质条件适应性强、施工便捷、造价低等优点[1]，得到广泛应用。对于挖入式港池而言，板桩码头存在向内侧或向外侧弯折的转角段，见图1。

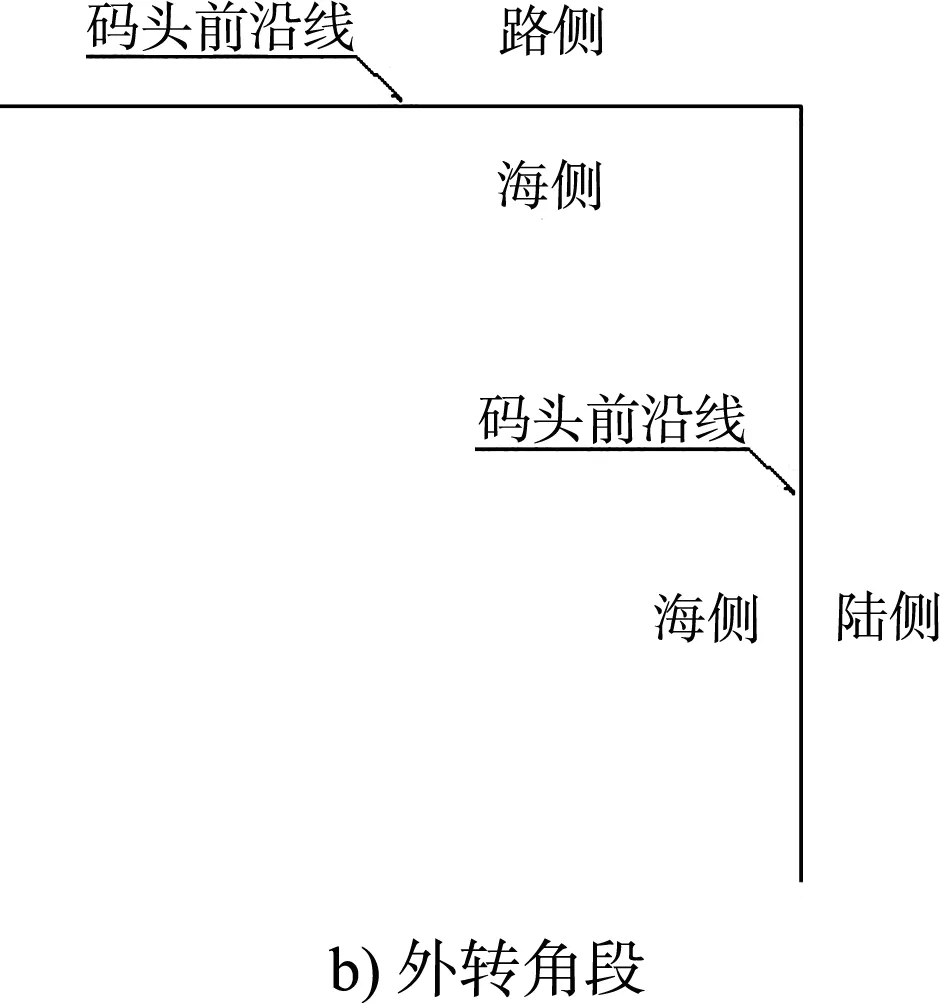
图1 板桩码头转角段

转角段具有明显的空间特征，目前国内外针对板桩码头转角段受力与变形的相关研究较少。板桩码头转角段设计一般采用板桩码头标准段的计算成果。为了探讨板桩码头转角段的受力与变形特性，本文以广州南沙港某Z型钢板桩码头为例，运用国际大型通用岩土有限元软件建立三维有限元模型，对板桩码头标准段、内转角段和外转角段的受力与变形特性进行对比分析，为板桩码头转角段的精细化设计提供参考。

1 工程概况

广州南沙港某板桩码头顶面高程为5.6 m，港池前沿设计底高程为-5.7 m。前墙采用Z型钢板桩，顶高程1.9 m、底高程-19 m。锚碇结构采用现浇C40钢筋混凝土锚碇墙，顶高程4.0 m、墙高4 m、墙厚0.6 m。板桩墙后回填中粗砂，锚碇墙前回填10～100 kg块石，顶宽10 m。前墙与锚碇墙采用钢拉杆相连，钢拉杆间距2.1 m、安装高程为1.5 m、直径为70 mm。地基表层及下卧的淤泥和淤泥质土采用真空联合堆载预压进行处理，处理范围为码头前沿线向海侧25 m至码头前沿线向陆侧45 m。码头典型断面见图2。

图2 码头典型断面(高程：m)

2 模型建立

2.1 土体本构模型及单元选取

土体本构模型采用小应变土体硬化模型(简称HSS模型)，该模型为弹塑性双曲线模型，其在土体硬化模型的基础上引入了小应变属性[2]，考虑了土的受荷历史和刚度的应变相关性，可模拟从小应变到大应变范围内土体的不同响应[3]。

为真实模拟板桩-土的相互作用，用板单元模拟板桩结构，用实体单元模拟土体、回填材料，在板桩与土体之间加入接触界面单元，用点对点锚杆单元模拟拉杆，锚碇墙也采用实体单元。板桩码头不同结构段的三维有限元模型见图3。

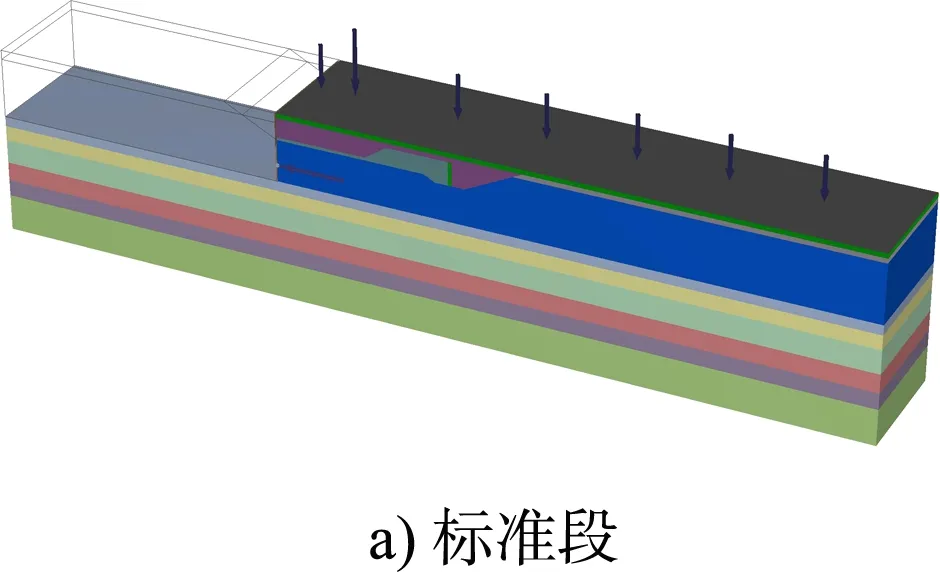
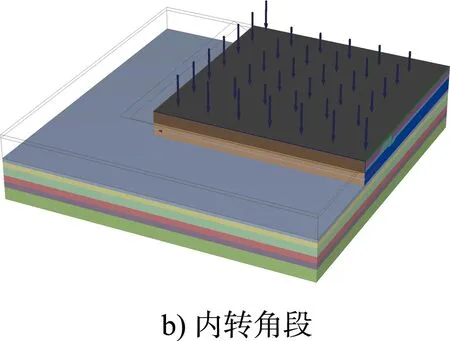
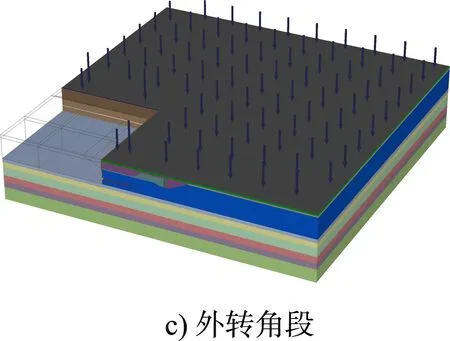
图3 板桩码头三维有限元模型

2.2 土体参数取值

反映土体特性的相关参数取值是岩土有限元计算的关键，常规地勘报告往往无法提供所有土体建模参数，需要参考相关的理论研究和工程经验综合考虑确定。文献[4-6]对HSS模型整套参数的取值进行了深入研究，为工程应用提供了借鉴。本文土体强度根据地勘报告的三轴试验取值，变形模量根据地勘报告的压缩模量由经验公式计算确定，土体参数见表1。

表1 土体参数

2.3 模型边界

为了减弱边界效应，模型边界越大越好，但计算量相应增加。综合考虑模型的精度和计算效率，模型宽度方向(即模型X轴边界)为码头前沿线向海侧50 m至码头前沿线向陆侧100 m，共150 m；模型长度方向(即模型Y轴边界)标准段模型选取了10倍拉杆间距，即21 m，转角段模型基于对称性考虑，长度与宽度取值相同，为150 m；模型高度方向(即模型Z轴边界)为码头顶高程至⑦1黏土-粉质黏土底高程。

2.4 拉杆、锚碇墙交叉区处理

由于板桩码头内转角段两侧拉杆和锚碇墙在平面位置上相互交叉，为了保证两个方向拉杆和锚碇墙的受力与变形互不干扰，在拉杆交叉处将拉杆沿竖向错开布置，一侧拉杆安装高程取1.5 m(对应锚碇墙的底高程为0 m)、另一侧取0.5 m(对应锚碇墙的底高程为-1 m)，在锚碇墙交叉处设置结构缝处理。

2.5 施工阶段

在软件中定义施工阶段如下：1)场地初始应力平衡；2)场地开挖至拉杆和锚碇墙底高程；3)打设前墙钢板桩，现浇锚碇墙，安装拉杆；4)墙后回填，上部结构施工；5)墙前港池开挖至设计底高程；6)施加码头前沿堆货荷载、剩余水压力、波吸力或系缆力等荷载。

3 计算结果及对比分析

3.1 前墙

分别提取标准段、内转角段和外转角段前墙的弯矩和位移云图，见图4、5。

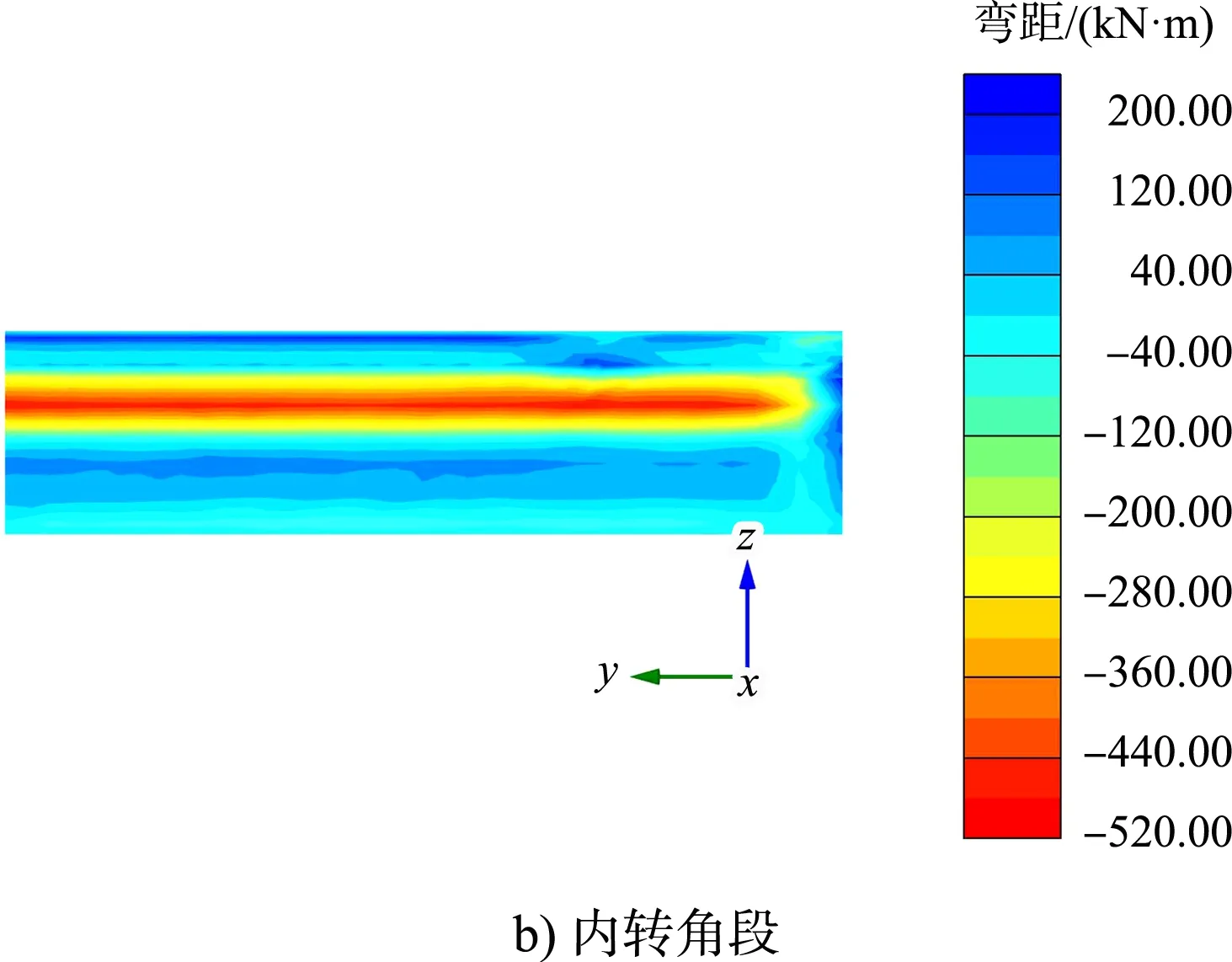
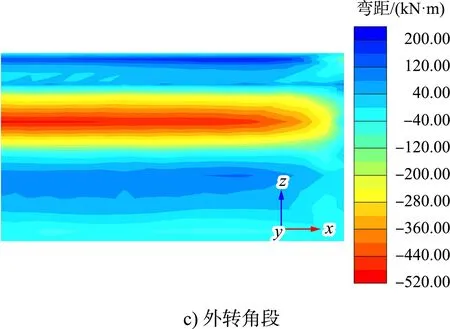
图4 前墙弯矩云图

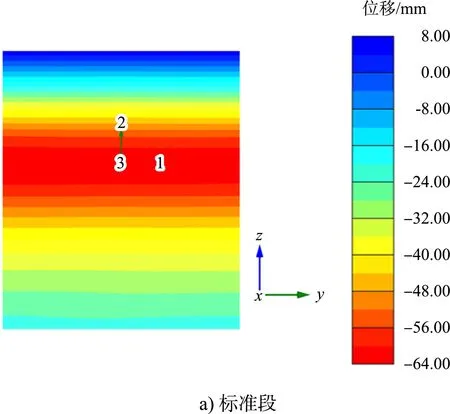
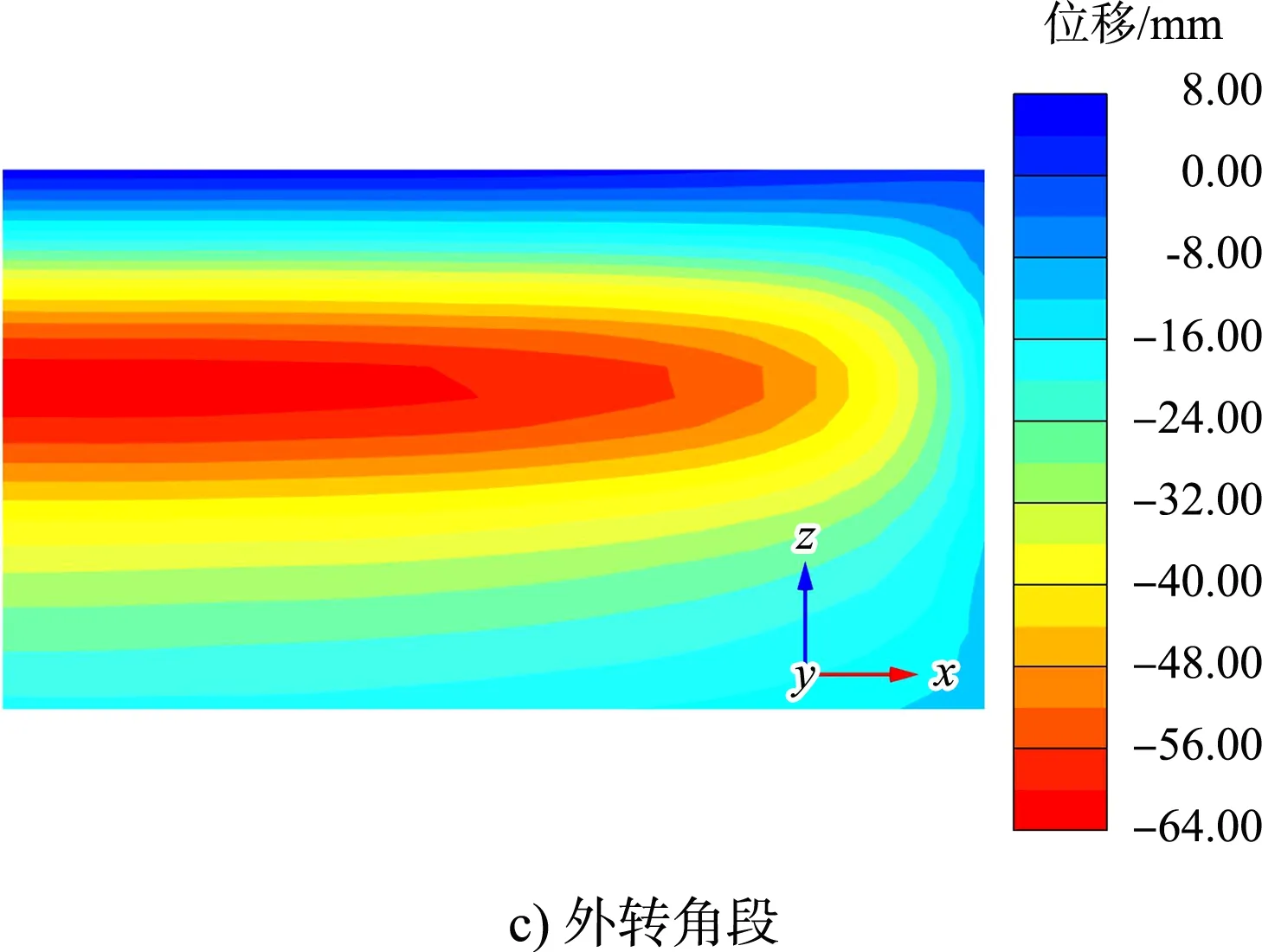
图5 前墙位移云图

经数据提取分析可知，3种结构段前墙的弯矩和位移最大值基本一致，竖向分布基本相同，在-3.4 m处弯矩最大，在-4.8 m处位移最大。为更清晰地表示前墙的受力变形规律，分别提取3种结构段前墙水平方向的弯矩和位移最大值，取相反值进行数据处理，见图6、7。

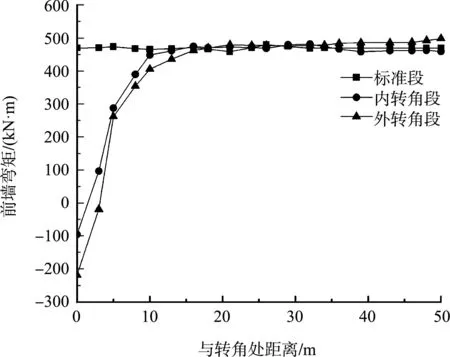
图6 前墙弯矩最大值相反值分布对比

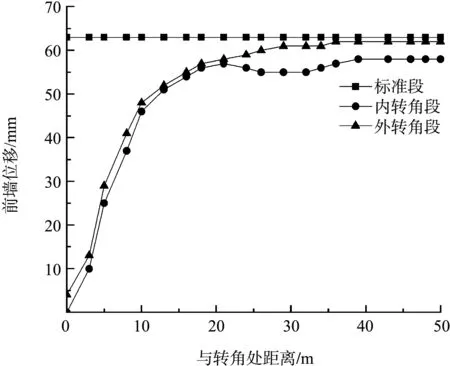
图7 前墙位移最大值相反值分布对比

从图6、7可见，标准段前墙的弯矩和位移水平分布都很均匀，内转角段和外转角段弯矩和位移在转角处均最小，随着与转角处距离的增加而增大，弯矩在距转角点约15 m处达到峰值并趋于平稳，位移在距转角点约20 m处达到峰值并趋于平稳。

3.2 拉杆

分别提取标准段、内转角段和外转角段的拉杆拉力进行数据处理，见图8。

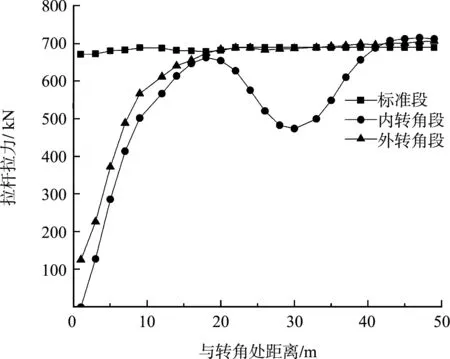
图8 拉杆拉力分布对比

从图8可见，3种结构段的拉杆拉力最大值基本一致。标准段的拉杆拉力分布很均匀；内转角段在转角处拉杆几乎不受力，拉杆拉力随着与转角处距离的增加而增大，在距转角点约20 m处达到峰值后又小幅回落，然后在距转角点约40 m处再次升至峰值并趋于平稳；外转角段在转角处拉杆拉力较小，约为最大值的1/6，随着与转角处距离的增加而增大，在距转角点约20 m处达到峰值并趋于平稳。

3.3 锚碇墙

提取标准段、内转角段和外转角段锚碇墙的位移云图，见图9。

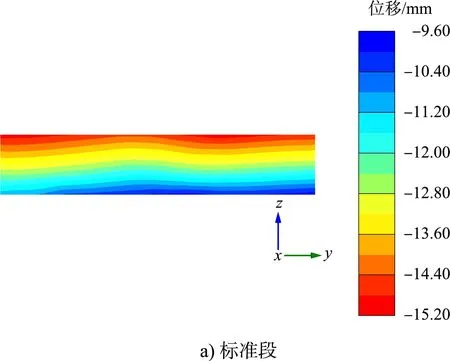
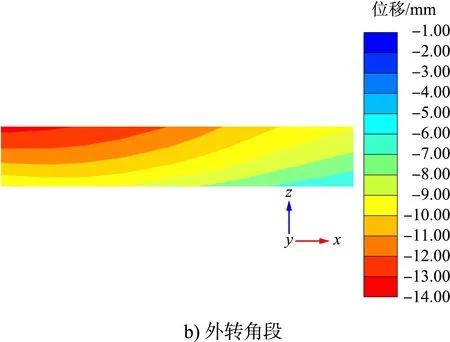
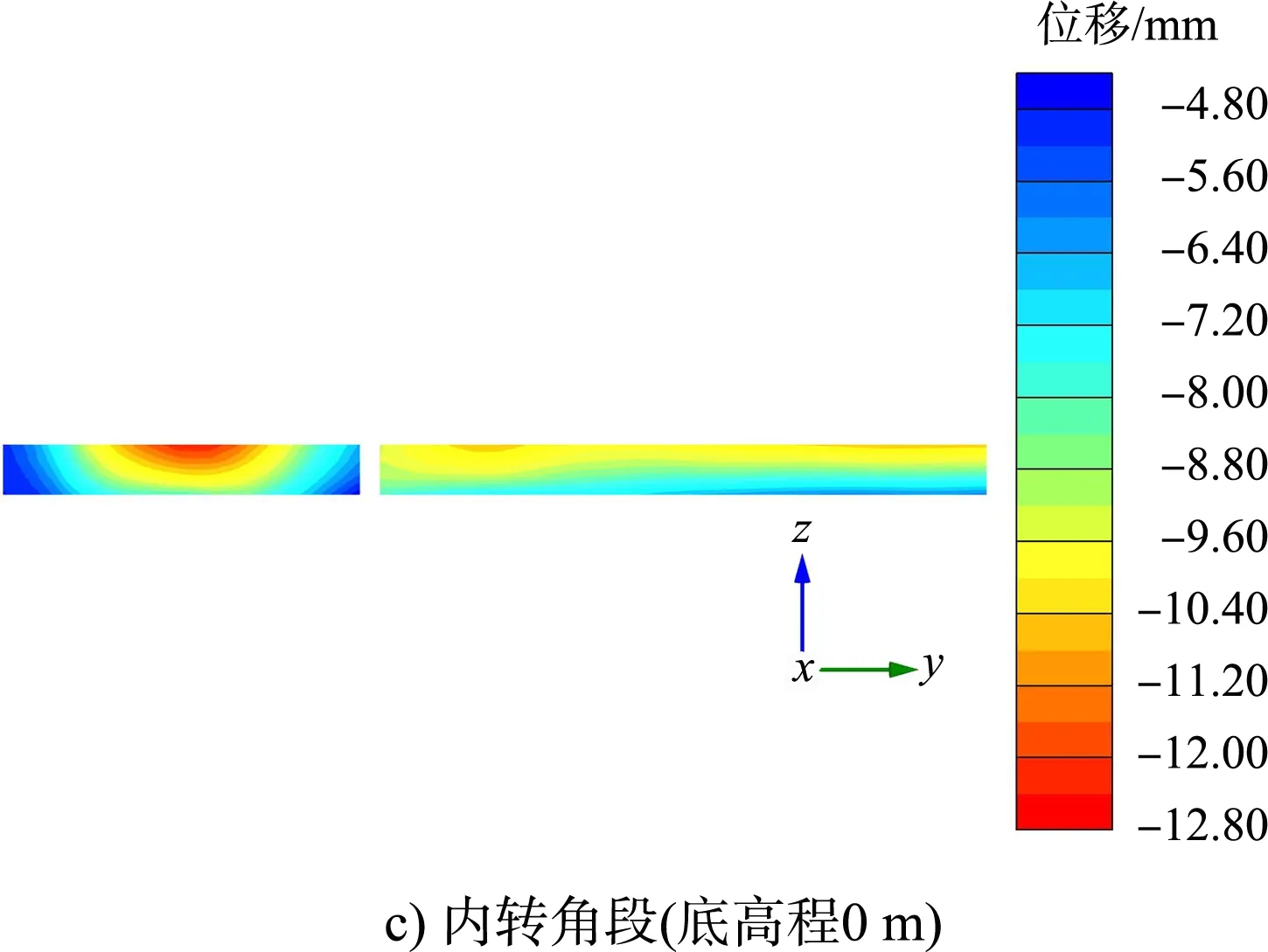
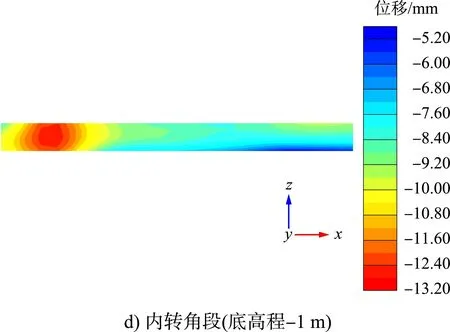
图9 锚碇墙位移云图

从图9位移云图可见，3种结构段的锚碇墙位移最大值相差不大。分别提取3种结构段前墙水平方向的位移最大值相反值进行数据处理，见图10。

图10 锚碇墙位移绝对值的最大值分布对比

从图10可知，标准段锚碇墙水平方向的位移分布很均匀；内转角段和外转角段在转角处位移均最小；外转角段锚碇墙的位移随着与转角处距离的增加而增大，在距转角点约40 m处达到峰值并趋于平稳；内转角段由于两个方向的拉杆竖向相互错开，锚碇墙的高度有差异，因此锚碇墙的位移分布较为复杂，底高程为0 m的锚碇墙距转角点约15 m处位移最大，底高程为-1m的锚碇墙距转角点约30 m处位移最大。

综上所述，根据前墙、拉杆、锚碇墙的受力与变形特征，Z型钢板桩码头的转角段范围为15～40 m，在该范围内前墙的弯矩和位移、拉杆拉力、锚碇墙位移均比标准段小，这与转角处的边界效应以及拉杆、锚碇墙在该处交错布置的空间效应有关。