基于倾斜变形的边坡临界滑动面确定方法研究
2022-11-01菅永明屈晓英袁维赵刚
菅永明, 屈晓英, 袁维, 赵刚
(1.贵州紫望高速公路有限公司, 安顺 560800; 2. 石家庄铁道大学土木工程学院, 石家庄 050043; 3. 盘州市水务局, 盘州 553500 )
确定边坡临界滑动面是边坡稳定性分析工作中需要解决的关键问题之一。强度折减法可以计算得到较为合理的边坡安全系数,但是如何通过该方法寻找边坡临界滑动面,截至目前尚未达成统一认识[1-2]。Griffiths等[3]通过对算例计算发现边坡破坏发生在土体剪切强度不足以抵抗剪应力的区域内,坡体变形后的网格会出现一条畸变带,可将这条畸变带视为边坡临界滑动面。 Matsui等[4]认为自然边坡的临界滑动面可定义为累计剪应变是某个值的等值线,开挖边坡的临界滑动面可定义为剪应变增量是某个值的等值线。Cheng等[5]认为边坡临界滑动面可由最大剪切应变和最大剪切应变增量云图来表征,且二者给出的临界滑动面类似,并在二维边坡稳定性分析中选用最大剪切应变增量表征的边坡临界滑动面进行了强度折减法和极限平衡法的研究比较。Zheng 等[6]在对边坡进行稳定性分析时,给出了定义边坡潜在滑动面满足的常微分方程的初值问题,利用数值方法计算该方程就可以得到边坡临界滑动面。Lin 等[7]认为边坡处于临界破坏状态时,可选取位移等值线来判断边坡的滑动面。靳付成[8]在计算时采用了塑性区贯通、边坡剪应变的速率、单元塑性应变能、以及边坡塑性应变矢量等不同的方法确定边坡的临界滑动面,认为塑性区贯通的方法是确定边坡潜在危险滑动面的最直观的方法,并验证了吴顺川等[9]用剪应变速率方法确定边坡潜在滑动面和用等效塑性应变、广义剪应变或广义塑性应变方法得到的滑动面位置相差不大的结论。袁维等[10]认为边坡潜在滑动面上的点为边坡深度方向上沿垂直滑面方向位移变化率最大的点,通过强度折减法使边坡达到临界破坏状态,在搜索区域布置离散点,寻找到表征边坡滑动面的位置点并进行平滑处理,从而得到边坡的临界滑动面;李建朋等[11]认为边坡滑动体内部各点速率大于稳定体内部各点速率,滑动面是由一系列速率发生突变的点组成,通过强度折减法使边坡达到临界破坏状态,寻找到这些速率突变点串联起来并利用最小二乘法进行平滑处理即可得到临界滑动面;Zheng 等[12]和孙冠华等[13]认为边坡临界滑动面上的点是沿深度方向等效塑性应变最大的位置,通过强度折减法使边坡达到临界破坏状态,搜索沿深度方向等效塑性应变最大点并采用最小二乘法对数据拟合平滑处理得到边坡临界滑动面;聂治豹等[14]在孙冠华等[13]的基础上,搜索处于临界破坏状态的边坡沿深度方向等效塑性应变最大点,选用小波变换法搜索边坡滑动面。孙冠华等[15]在文献[13]的基础上将二维问题深化为三维问题,选用薄板光顺样条函数插值得到三维边坡临界滑动面。
综上所述,基于强度折减法寻找边坡临界滑动面的研究工作多是以二维边坡为研究对象进行研究分析,寻找三维边坡临界滑动面的研究工作相对较少。而实际生活中的滑坡体为三维形状,鉴于此,在总结前人在该领域的研究基础之上,现建立三维边坡数值模型并选用强度折减法进行计算,寻找边坡临界状态时对应的倾斜变形规律,提出基于倾斜变形的三维边坡临界滑动面确定方法。
1 基本原理
1.1 空间倾斜角度计算
为了阐明边坡上某点空间倾斜角度计算的基本原理,本文建立了三维边坡及空间角度变化计算模型,其示意图如图1所示。

H、W、 β分别为边坡模型的高度、宽度和坡角;δ为边坡变形滑动过程中倾斜变形计算长度只发生倾斜变化时产生X、Y、Z三个方向的合位移;α为三维边坡临界状态时的空间倾斜角度变化值图1 三维边坡模型及空间角度变化Fig.1 Model for three-dimensional slope and spatial angle change
如图1所示,AO为边坡初始离散点的倾斜变形计算长度,其值为d,经强度折减计算至临界状态后的位置为A′O′;BO′是假设倾斜变形计算长度在边坡变形滑动后不产生角度变化,仅产生空间位移变化的情况;A′O′是倾斜变形计算长度在边坡变形滑动后既产生空间位移变化又产生空间角度变化的情况。假设A点在临界状态时产生的X、Y、Z方向的位移分别为x1、y1、z1,O点在临界状态时产生的X、Y、Z方向的位移分别为x2、y2、z2,则由图1中几何关系有
(1)
(2)
根据式(1)和式(2)中可以求解出三维边坡临界状态时的空间倾斜角度变化值α。
1.2 基于倾斜变形的滑动面确定方法
边坡处于临界破坏状态时,滑动面将边坡体划分为稳定体和滑动体两个部分。稳定体的节点空间位移仅仅是由单元的变形产生,滑动体的节点空间位移由单元的变形和滑动的空间位移组成,而滑动作用引起的节点空间位移要显然大于单元变形引起的节点空间位移,滑动体相对于稳定体产生无限制的滑移,滑动面两侧将产生明显的空间位移差[8]。图2为简化的二维边坡临界滑动面,沿边坡深度方向等距离布置离散点,1~5号离散点位于同一直线上,并以离散点为中心选择一定倾斜变形计算长度计算各离散点的空间倾斜角度。当边坡处于临界破坏状态时,必然已经产生空间不同方向的位移变形,根据式(1)和式(2),可计算各离散点的空间倾斜角度变化。其中,1号和2号离散点倾斜变形计算长度的两端全部位于滑动体中,其空间倾斜角度变化均由滑动体产生的不同方向的位移(包括单元变形和滑动位移)计算得到;4号和5号离散点倾斜变形计算长度的两端全部位于稳定体中,其空间倾斜角度变化均由稳定体产生的不同方向的位移(仅是单元变形位移)计算得到;而3号离散点倾斜变形计算长度的两端分别位于滑动体和稳定体中,且中点O位于边坡临界滑动面上,其空间倾斜角度变化由滑动体产生的不同方向的位移(A点)和稳定体产生的不同方向的位移(B点)计算得到。显然,3号离散点倾斜变形计算长度顶端A点产生的空间位移要大于底端B点产生的空间位移,此时,3号离散点产生的空间倾斜角度要大于其他任意离散点的空间倾斜角度。由此可知,在三维边坡中,临界滑动面可由一系列空间倾斜角度最大值的位置点来表征。由此可知,三维边坡基于倾斜变形确定临界滑动面的计算步骤如图3所示。

图2 基于倾斜变形的滑动面确定方法Fig.2 Slip surface determination method based on inclined deformation

图3 滑面搜索计算步骤Fig.3 Steps of searching for slip surface
2 算例分析
按图1所示比例建立坡高H=50 m,坡角β=45°,宽高比W/H=2的三维边坡计算模型并施加全约束边界条件,岩体材料重度取22.5 kN/m3,特征参数mb=1.235 90、s=0.000 24、a=0.531 27,弹性模量为1 140 MPa,泊松比为0.36。采用等效强度参数的Mohr-Coulomb准则代替Hoek-Brown准则进行强度折减计算,等效摩擦角为53.6°,等效黏聚力为91.6 kPa。经强度折减法使边坡达到临界状态,按照下面的步骤即可得到该边坡的临界滑动面。
(1)全约束边界条件下的边坡变形呈对称特性,因此对三维边坡沿边坡宽度方向对称取半进行分析,根据位移云图估计三维边坡发生滑坡的大致范围,由此确定三维边坡临界滑动面的搜索范围,如图4所示,黑色直线与边坡边界围成的三维空间区域即为三维边坡临界滑动面的搜索范围。
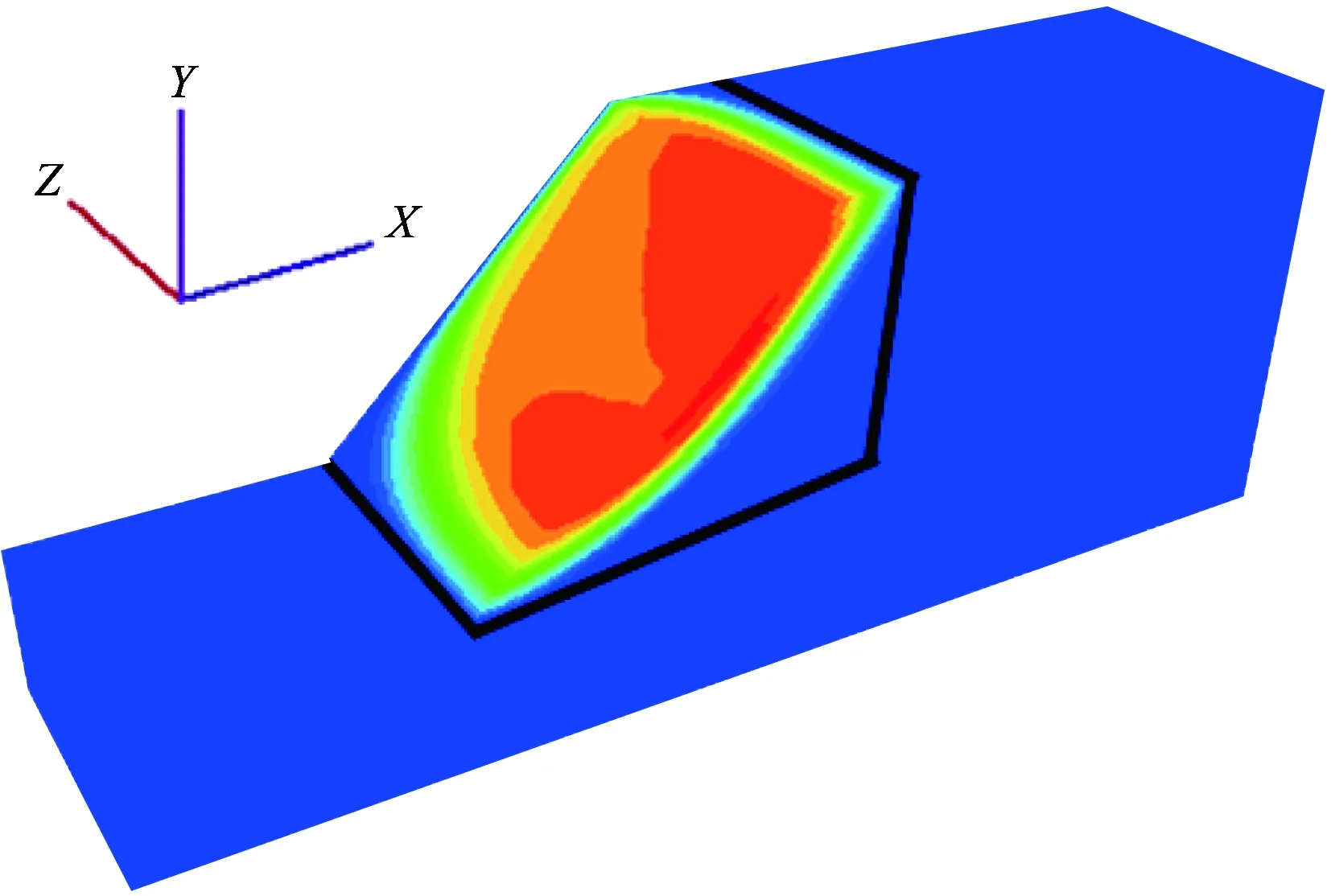
图4 边坡临界滑动面搜索范围Fig.4 Search range of critical slip surface of slope
(2)在搜索范围内沿边坡表面宽度方向和垂直宽度方向分别等距布置若干条直线,并在每条直线上等距离布置若干离散点,如图5所示。计算若干以离散点为中心沿直线方向取一定倾斜变形计算长度时产生的空间倾斜角度变化(倾斜变形计算长度的端部位于临界滑动面的搜索边界处,不计算由全约束边界产生的空间倾斜角度),提取每条直线上计算所得的空间倾斜角度最大值的离散点三维坐标(剔除多余空间点),即为表征三维边坡滑坡周界的位置点。
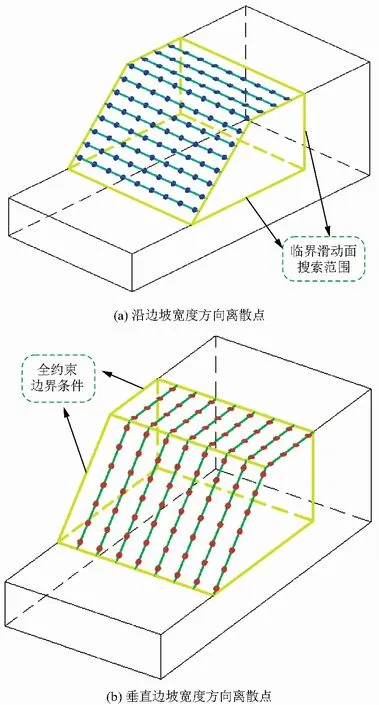
图5 边坡表面离散点布置Fig.5 Arrangement of discrete points on slope surface
(3)在滑坡周界范围内沿所估计的滑坡范围水平方向等距布置一系列竖直线,并沿竖直线等距布置若干离散点(剖面如图6所示),计算若干以离散点为中心沿竖直线方向取一定倾斜变形计算长度时产生的空间倾斜角度变化,提取每条竖直线上计算所得的空间倾斜角度最大值的离散点三维坐标,即为表征三维边坡内部临界滑动面上的位置点。
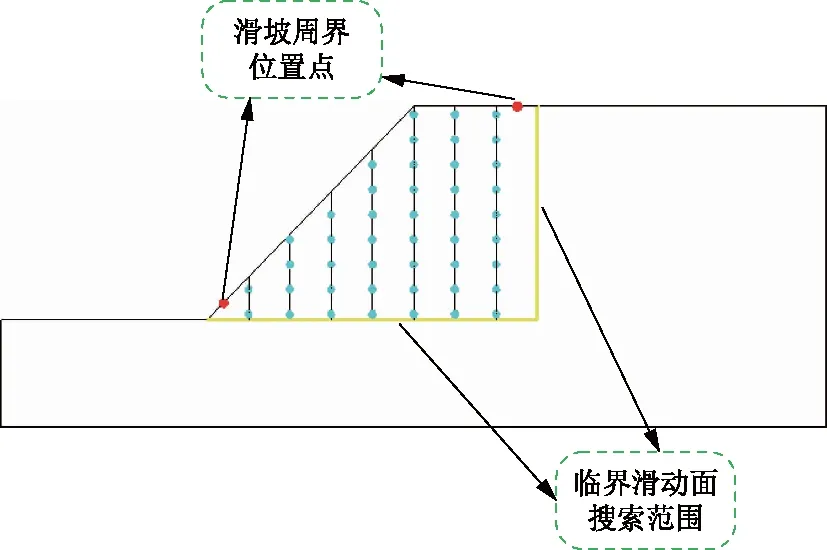
图6 边坡体内部垂向离散点布置Fig.6 Arrangement of vertical discrete points inside the slope
(4)将步骤(2)和步骤(3)所得到的一系列三维空间点相连,采用局部加权回归散点平滑方法做平滑处理,并将曲面在边坡范围外的多余部分进行裁剪即可得到满足合理性要求的三维边坡临界滑动面,如图7所示。
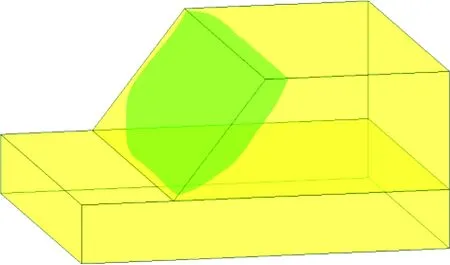
图7 三维边坡临界滑动面示意图Fig.7 Schematic diagram of 3D slope critical slip surface
3 讨论
按本文所述方法所提取的一系列表征三维边坡临界滑动面的空间位置点与空间倾斜角度的最大值和离散点距离的大小有关,而空间角度值的计算涉及选取的倾斜变形计算长度的大小,因此倾斜变形计算长度和离散点的距离取值可能会对三维边坡临界滑动面的搜索结果产生影响。为此,本文从倾斜变形计算长度大小和离散点布置的疏密程度两个方面进行探讨。由于需要提取的表征三维边坡临界滑动面的离散点是倾斜变形计算长度的中点,所以理论研究分析时忽略倾斜变形计算长度的重合部分。分别选取倾斜变形计算长度d=0.1、0.2、0.5、0.8 m和离散点间距w=0.2、0.5、0.8、1、1.5、2、4、8 m进行三维边坡滑动面的计算分析探讨。在采用局部加权回归散点平滑方法对表征边坡临界滑动面的空间位置点做平滑处理时选取相同的窗宽值。
3.1 不同倾斜变形计算长度的边坡临界滑动面
按上述方法,计算取不同d值时各个离散点产生的空间倾斜角度进而得到满足合理性要求的边坡临界滑动面。结果显示,取相同w值时,以不同d值计算所得的三维边坡临界滑动面位置相差不大,限于篇幅,仅以w=1 m时不同d值的计算结果示例说明,如图8所示。

图8 不同d值的边坡临界滑动面Fig.8 The critical slip surface of slope with different d values
3.2 不同离散点间距的边坡临界滑动面
按照上述方法,计算不同的w值时各个离散点产生的空间倾斜角度进而得到满足合理性要求的边坡临界滑动面。结果显示,相同d值时,随离散点间距增大的表现大致相同,限于篇幅,仅以d=0.8 m时不同w值的计算结果示例说明。在w=0.2、0.5、0.8、1、1.5、2 m可计算出符合全约束边界条件的三维边坡临界滑动面,且临界滑动面的位置相差不大,而w=4、8 m时计算所得的临界滑动面与边坡坡面边界不相交(坡顶处表现明显),不符合全约束边界条件下的真实滑动面形状,且w=8 m时的滑动体范围明显大于真实滑动体范围,如图9~图11所示。

图9 符合全约束边界条件的边坡临界滑动面Fig.9 The critical slip surface of the slope with fully constrained boundary condition

图10 不符合全约束边界条件的边坡临界滑动面Fig.10 The critical slip surface of slope which does not meet the fully constrained boundary condition
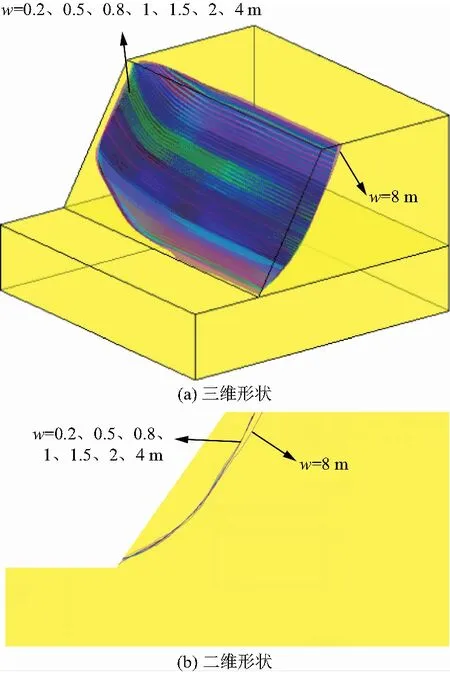
图11 不同w值组合的边坡临界滑动面Fig.11 The critical slip surface of slope with different combination of w values
4 结论
开展了基于空间倾斜变形确定三维边坡临界滑动面的搜索方法研究,得出如下结论。
(1)强度折减使边坡达到临界破坏状态时,可根据位移云图大致确定三维边坡滑动体的大致范围,进而在该范围沿边坡表面布置水平线及坡体内部布置直线来确定三维边坡临界滑动面的搜索路径。
(2)全约束边界条件下的三维边坡对称取半进行分析,临界滑动面可由一系列搜索路径上的空间倾斜角度最大值的位置点来表征,通过对这一系列空间点采用局部加权回归散点平滑方法做平滑处理即可得到满足合理性要求的三维边坡临界滑动面。
(3)通过讨论发现,本次选取不同倾斜变形计算长度计算搜索路径上离散点的空间倾斜角度对三维边坡临界滑动面的位置和形状影响不大,而随着离散点间距的减小,临界滑动面的形状接近于真实的全约束边界条件下的三维边坡临界滑动面。
