鸭翼位置对二元机翼静气弹特性的影响

2022-11-01苏新兵马斌麟

兵器装备工程学报 2022年10期

王振,苏新兵,王宁,马斌麟

(1.空军工程大学航空工程学院，西安 710038； 2.空军工程大学航空机务士官学校，河南信阳 464000)

1 引言

现代飞行器结构柔性越来越大，在对机翼气动参数优化过程中，就必须要考虑到弹性变形影响。近年来随着复合材料的应用，柔性机翼的设计理念越来越受重视。目前已有许多对鸭式布局的研究，鸭翼面产生的涡系能对主翼涡产生有利干扰，控制主机翼表面附面层分离，使主机翼的失速迎角和最大升力系数明显增大。空军工程大学的张冬等通过对比单独鸭翼涡以及前、后掠翼布局中鸭翼涡与机翼前缘涡的干扰分析了鸭翼涡流动机理，文献[4]中通过数值模拟研究了鸭翼对翼身融合布局飞机低速纵向气动特性的影响，北京航空航天大学的陈庆民等也对非定常运动中鸭翼高度对战机纵向气动特性的影响进行了揭示。这些研究基本集中于刚性机翼方面，关于鸭翼对柔性机翼静气弹特性影响的研究十分有限。

对机翼性能的研究必须先从翼型气动特性和弹性变形特性开始进而延伸到三维有限翼展的研究，因此本文中以NACA64A010翼型为基准，采用CFD/CSD松耦合数值仿真计算方法，研究亚音速条件下鸭翼位置对二元翼型气动特性和弹性变形特性的影响，为进一步研究鸭翼对前掠机翼静气动弹性发散特性的影响提供参考。

2 计算方法及验证

本研究在处理二维翼型计算问题中采用基于CFD/CSD松耦合的静气动弹性计算方法。松耦合方法即分离解法，其不需要耦合流、固控制方程，而是按设定顺序在同一求解器或不同求解器中分别求解流体控制方程和固体控制方程，通过流固交界面(FS Interface)把流体域和固体域的计算结果互相交换传递,待此时刻收敛达到要求，进行下一时刻的计算，依次而行求得最终结果。在每一次迭代过程中，采用常体积转换(constant volume transformation，CVT)方法进行气动力与结构位移插值传递。流体域将气动力传递给固体域完成相应静力学计算后，产生的结构位移导致流体域网格质量变差，再采用径向基函数方法对流体域网格进行更新优化，以满足下一次迭代求解的要求。

流场计算是耦合计算的重点，CFD求解器采用Navier-Stokes(N-S)方程作为描述流体运动控制方程，根据Einstein求和约定，在笛卡尔坐标系中，不考虑热源的N-S方程积分守恒形式可表达为：

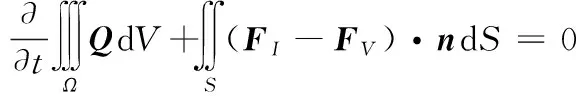
(1)

式中：为状态矢量项；和分别为无粘和粘性通矢量项；为控制体；表示控制体表面；为表面微元外法向向量。

因为平均N-S方程的不封闭性，需要引入湍流模型来封闭方程组，本文采用稳定、收敛性良好且适用于低雷诺数条件的Spalart-Allmaras(S-A)模型。流体控制方程的离散采用有限体积法，在结构域计算中，针对本文所研究的二元翼型静气弹特性问题只关心响应结果而不关心响应过程的特点，借助结构静力学便可满足本文静气弹特性分析需求。固体控制方程的离散则采用有限元方法。

为了验证二元翼型计算方法的准确性，本文使用NACA0012翼型的二维静气动弹性特性算例对所采用数值计算方法的有效性和精度进行验证,分别对流体域与结构域进行网格划分，流体域多边形网格单元数为18 527，结构域三角形网格单元数为4 163，划分后的网格如图1。

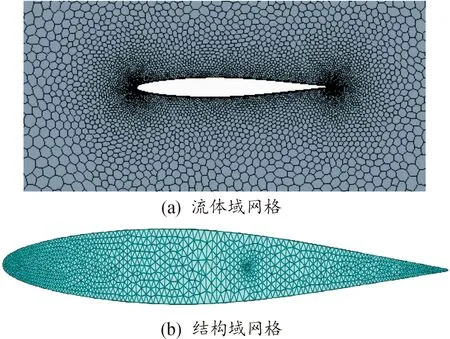
图1 NACA64A010翼型静气弹模型网格示意图Fig.1 The mesh used in static aeroelastic computation of NACA64A010 airfoil

在仿真计算中，流场计算条件为：=015，=6×10，=293.15 K。其中鸭翼为刚性，主翼为弹性，主翼机翼属性为=108 GPa，=0.33，=4 500 kg/m。其中：为弹性模量；为泊松比；为密度。

通过仿真计算得到NACA0012翼型在0～20°内多个攻角下的升力系数，如图2所示。对比实验值与仿真值发现，相同攻角下翼型的升力系数相近，最大误差小于5%。

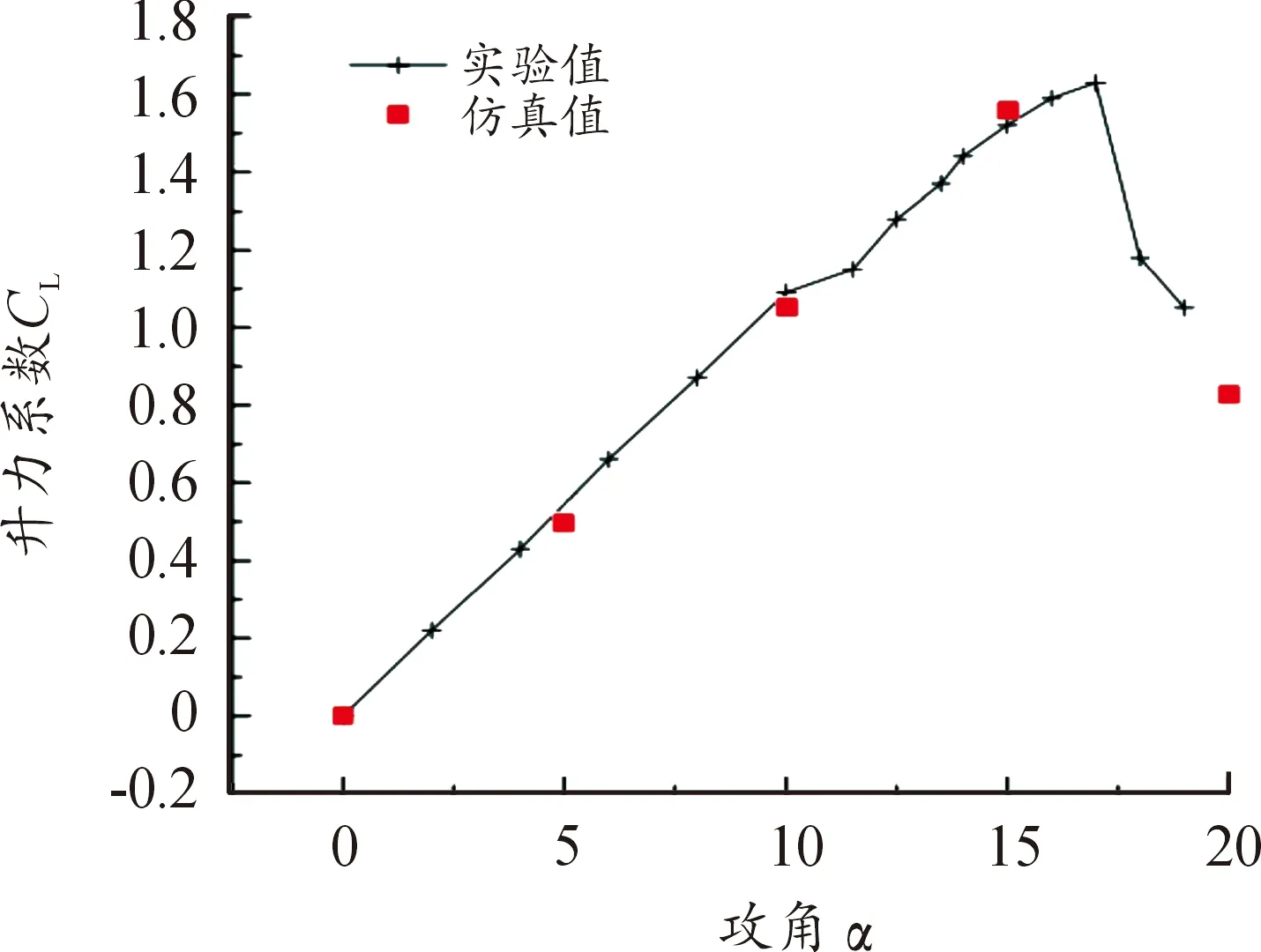
图2 NACA64A010翼型不同攻角下的升力系数曲线Fig.2 The lift coefficient of NACA64A010 airfoil under different angle of attack

通过多次流固耦合迭代计算，可得到=5°时翼型前缘点和后缘点的位移，将本次数值计算的结果与文献[10]中二维静气弹特性算例得到的翼型前、后缘点位移结果，如表1所示。本次仿真计算的收敛曲线如图2。

表1 计算结果与算例结果Table 1 The results of calculation compared with those of examples

由图3可知，迭代超过13000次后，残差稳定低于收敛精度10，计算收敛。在仿真计算中，计算平台、湍流模型以及网格划分的不同都会带来误差，但误差在5%以内，说明选取的仿真方法满足准确性要求。

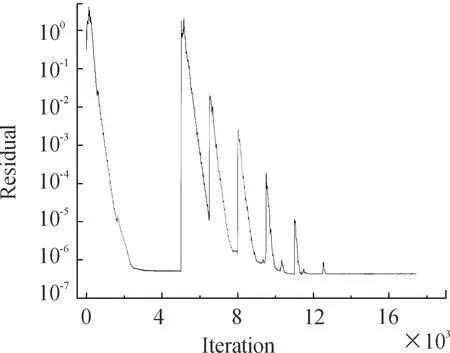
图3 收敛曲线Fig.3 Residual curve

3 计算模型

本文计算模型选取NACA64A010翼型，模型如图4所示。

图4 二元机翼模型示意图Fig.4 The model of two-demensional wing

模型主翼弦长=10mm，鸭翼弦长=500 mm，主翼刚心取至=055，鸭翼为固支状态。以主翼前缘点为坐标原点，建立二维坐标系，模型具体计算位置如表2所示。

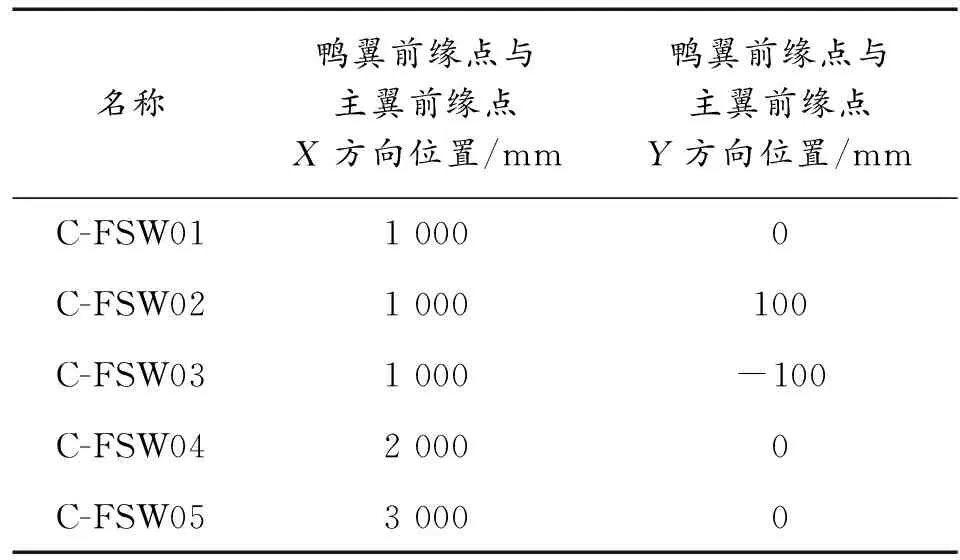
表2 模型简况Table 2 Models abbreviation

在计算过程中，固定主翼为弹性状态，鸭翼为刚性状态。对流体域进行六边形网格划分，对结构域进行三角形网格划分。选取合适的近壁面第一层网格高度，使值为1左右，远场边界到模型的距离为10倍主翼弦长。划分后网格如图5所示。

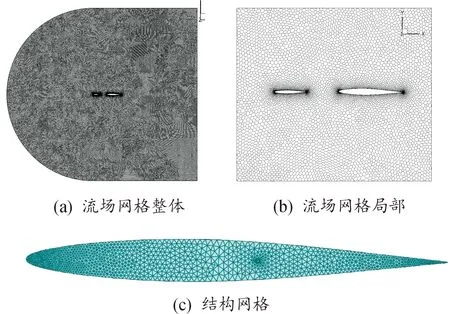
图5 C-FSW01模型网格示意图Fig.5 The mesh of C-FSW01 model

4 鸭翼高度影响

在=02,=4.11×10的条件下，对不同鸭翼高度模型的气动特性和弹性变形特性参数进行仿真计算，如图6所示。

4.1 气动特性

由图6(a)可知，无论是刚性状态还是弹性状态，3种模型的失速迎角均为=10°，3种模型升力系数随迎角的变化趋势类似，但弹性状态下升力线斜率要比刚性状态下的大。鸭翼高度不同，升力系数呈现显著差异，C-FSW02模型升力系数最高，弹性状态下max≈1.42，比C-FSW01模型高45.4%。这是由鸭翼扰流作用引起的，当鸭翼位于主机翼正前方时，其扰流作用最明显，破坏了主机翼的涡系，导致升力系数下降；当鸭翼位于主机翼上方时，鸭翼产生的旋涡对主机翼气流分离起到有利干扰，使升力系数增加。

由图6(b)可知，阻力系数随迎角不断增加，当<10°时，阻力系数随迎角增加而缓慢增加，因为此时机翼表面气流未分离，涡系结构未被破坏，阻力较小。当>10°时，阻力系数随迎角急剧增加，此时机翼表面气流分离严重；其中弹性机翼阻力系数比刚性机翼的大，且随迎角增大，弹性机翼阻力系数增量略有增加；鸭翼高度不同，阻力系数表现出明显差异，C-FSW02模型阻力系数较C-FSW03模型的小，说明高位鸭翼与主机翼相互耦合对气动性能起到了改善作用。

由图6(c)可知，不同鸭翼高度对最大升阻比影响显著，其中，高位鸭翼升阻特性最好，C-FSW02模型和C-FSW03模型均在=6°时获得最大升阻比，且最大升阻比均较C-FSW01模型高出125%。不同模型小迎角状态下，弹性条件下升阻特性均比刚性条件下的好，当>6°时，刚性条件下升阻特性更好，说明在>6°条件下，机翼的弹性变形已经破坏了机翼表面涡流。在α<12°范围内，高位鸭翼升阻特性最好，而大迎角时提升作用很小。

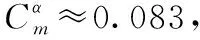
图6 不同鸭翼高度模型气动特性参数曲线Fig.6 Aerodynamic characteristics of models with different canard position in vertical direction

4.2 弹性变形特性

不同鸭翼高度对翼型气动特性产生明显影响，翼型表面气动力变化会引起其弹性变形的变化。本节对比了3种鸭翼模型的弹性变形情况，定义为前缘向挠度，弯曲变形量为前、后缘向的位移之和。

由图7可知，C-FSW01模型弹性变形近似为0，这是由其较小的气动力决定的，对于C-FSW02模型，前缘向挠度和弯度的变化趋势均为先增大后减小，当=10°时，和均达到最大值，此时max=14.134 23，max=2.857 95。对于C-FSW03模型，其前缘挠度和弯度变化趋势与C-FSW02模型相近，其和均略低于C-FSW03模型，且分别减少了约4.71%和4.56%。

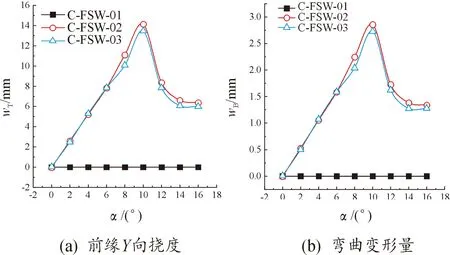
图7 主翼面弹性变形量曲线Fig.7 The elastic deformation characteristics of wing

4.3 流动机理分析

分别比较不同迎角状态下C-FSW01模型弹性状态机翼表面流线图，如图8。

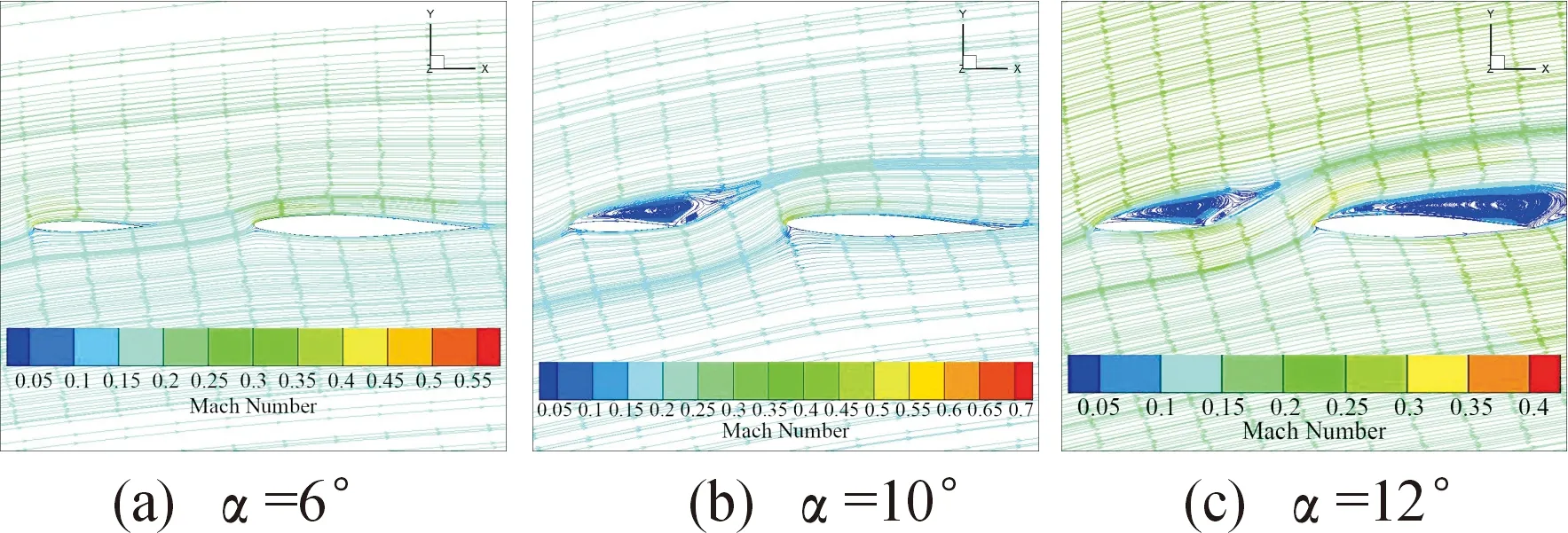
图8 C-FSW01模型不同迎角时的流线图Fig.8 The streamline of C-FSW01 model with different angle of attack

小迎角条件下，鸭翼和主翼翼面流动表现为附着流态，未出现明显漩涡，因此升力系数曲线为线性变化，弹性变形量和线性增加，由于鸭翼失速迎角较小，同时主翼对鸭翼的上洗作用加快了鸭翼表面气流分离，鸭翼上表面附着涡首先发生破裂，漩涡卷积但未破裂，主翼表面仍为附着流态，这就导致中等迎角情况下，升力系数非线性增加，当=10°时，主翼仍保持为附着流态，此时升力系数和弹性变形量均达到最大；随着迎角增加，主翼上表面旋涡破裂，流速变慢，导致主翼升力系数下降，弹性变形量也下降。

当=6°时，弹性条件下C-FSW01、C-FSW02和C-FSW03模型的流线图如图9。

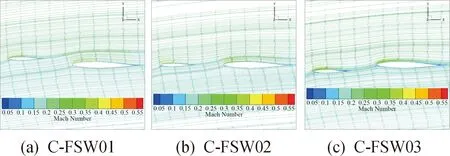
图9 α = 6°时模型的流线图Fig.9 The streamline of different models when α = 6°

由图9可知，在低马赫数、小迎角条件下，3种翼型均未出现明显气流分离，未出现明显旋涡，所以鸭翼对主翼的影响主要表现为扰流作用。鸭翼后缘流速出现明显下降，其中C-FSW01模型受到的影响最大，导致主翼上表面气流流速降低。C-FSW02模型中鸭翼对主翼产生的影响最小。

C-FSW01、C-FSW02和C-FSW03模型的压力云图如图10。由此可知，3种模型表面压力状况没有显著差异，主要因为低亚音速，小迎角条件下翼型表面气流处于附着流态。主翼上表面压力差距不大。但下表面略有差异，C-FSW02和C-FSW03模型相比，下表面压力较大，主要是因为C-FSW03模型鸭翼上表面高速气流绕过主翼下表面，使得主翼下表面压力降低，使得高位鸭翼模型升力特性优于低位鸭翼模型。

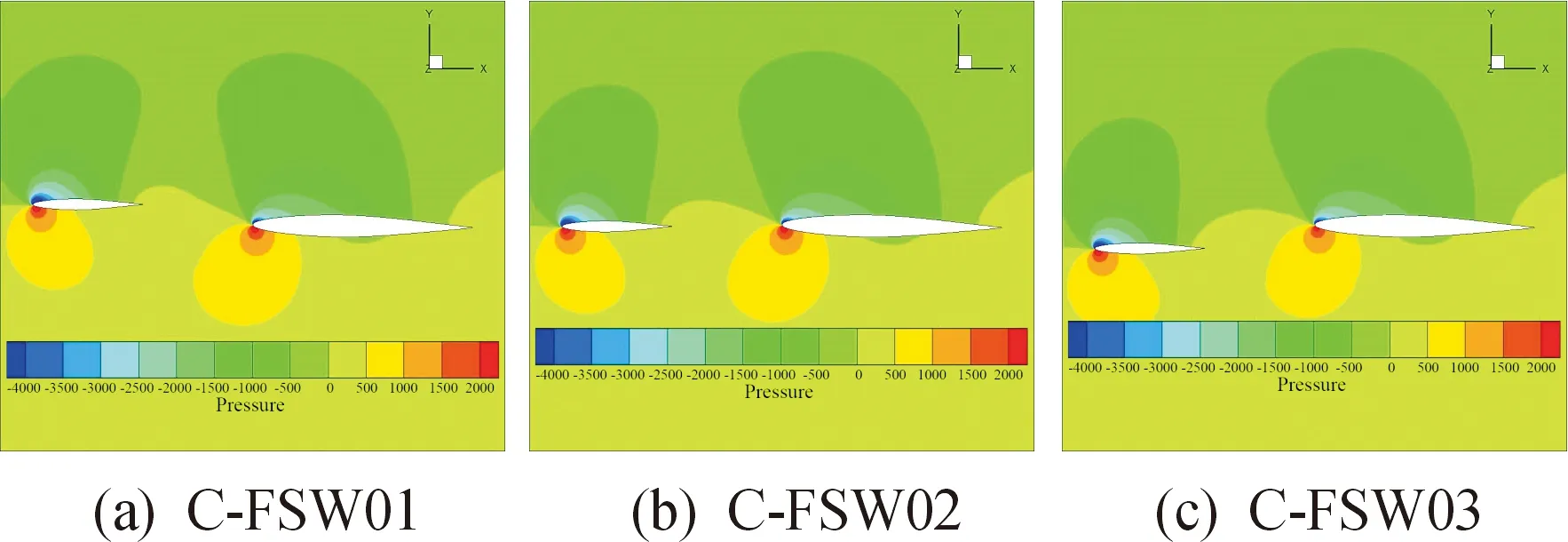
图10 α = 6°时模型的压力云图Fig.10 The pressure contour of different models when α = 6°

当=12°时，弹性条件下C-FSW01、C-FSW02和C-FSW03模型的流线图和压力云图如图11和图12。

图11 α = 12°时模型的流线图Fig.11 The streamline of different models when α = 12°

由图11可知，当=12°时，3种模型翼型表面均出现明显涡流，相比C-FSW01和C-FSW03模型，C-FSW02模型主翼涡与鸭翼涡产生有利干扰，鸭翼涡对主翼下洗作用明显，加快了主翼表面流速，同时，鸭翼涡对主翼涡产生一定的后推作用。

由图12可以看出，鸭翼涡的作用主要体现在了主翼上表面前端，C-FSW02模型主翼上表面压力系数明显较低，同时高位鸭翼上表面压力系数也较低，从而提供了一部分升力。

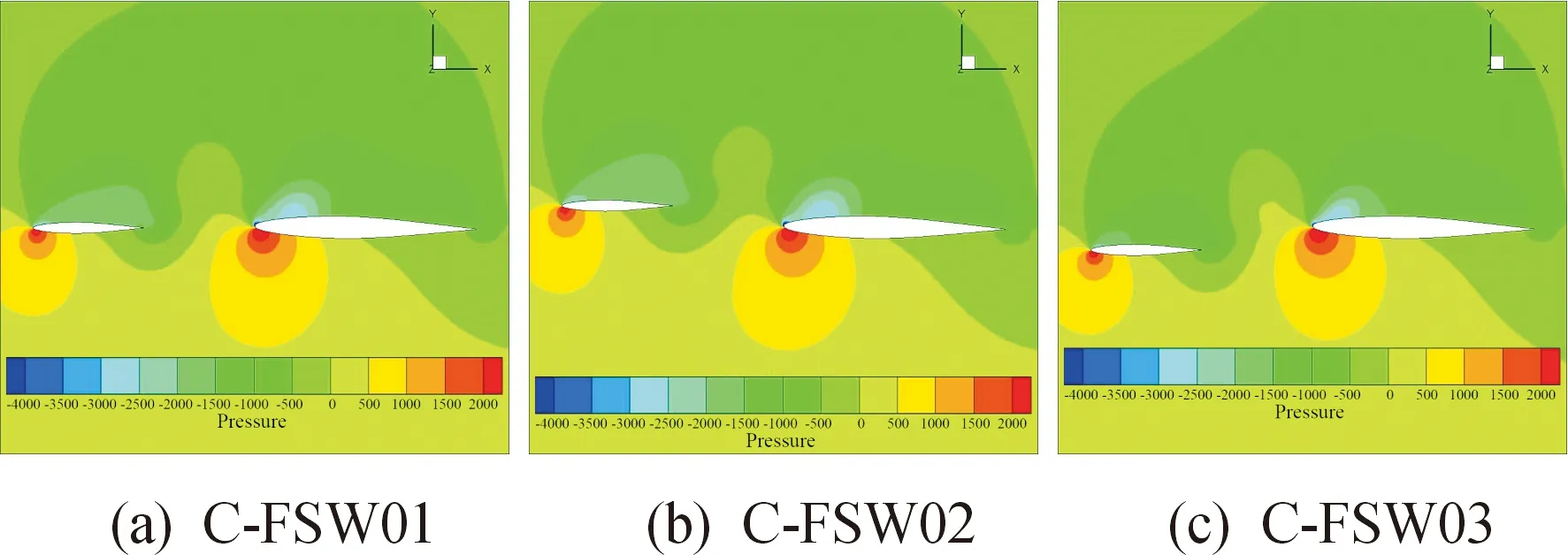
图12 α = 12°时模型的压力云图Fig.12 The pressure contour of different models when α = 12°

5 鸭翼距离影响

5.1 气动特性

为了进一步研究鸭翼位置对主翼静气弹特性的影响，在=02,=4.11×10的条件下，分别计算了不同鸭翼距离的升、阻力系数、升阻比以及俯仰力矩系数，如图13所示。

由图13(a)可知，相比较于近距鸭翼，远距鸭翼对升力系数有明显的改善作用。弹性状态下，C-FSW04模型和C-FSW05模型升力系数分别比C-FSW01模型的增大约42.89%和45.13%，且远距鸭翼达到升力系数最大值时，有一个较为明显的升力系数平台，提升了机翼的失速特性，且距离越大，平台越大，对于C-FSW04模型，平台范围为8°～10°，对于C-FSW05模型，平台范围为8°～12°。这是因为，鸭翼与主机翼位于同一水平高度，鸭翼位置越近，鸭翼涡对主机翼扰流作用越明显，导致大迎角时主机翼表面涡流结构完全破坏，升力系数下降。

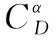
由图13(c)可知，相较于近距鸭翼，远距鸭翼升阻特性更好，其中C-FSW04模型和C-FSW05模型最大升阻比分别比C-FSW01模型的高出约126.40%和127.76%。其中，弹性状态下升阻特性相较于刚性状态下更优。

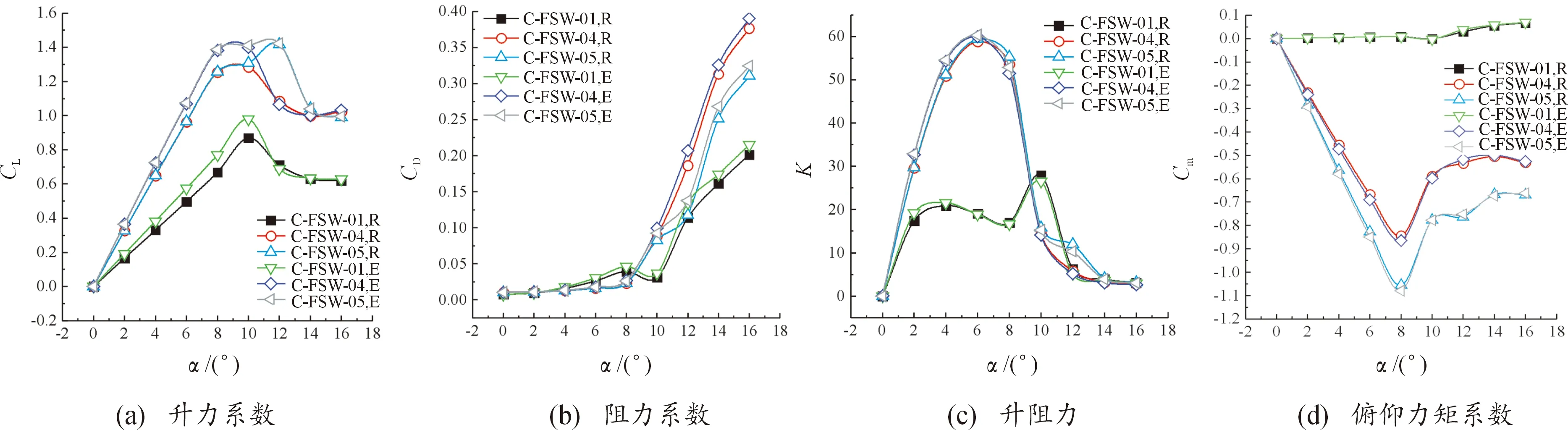
图13 不同鸭翼距离模型气动特性参数曲线Fig.13 Aerodynamic characteristics of models with different canard position in horizontal direction

5.2 弹性变形特性

由图14可知，不同鸭翼距离情况下，当迎角变化时，主翼变形情况略有不同。当<10°时，C-FSW04模型和C-FSW05模型和均线性增加。当>10°时，C-FSW04模型和非线性逐渐减小；C-FSW05模型和先增大后减小。当=10°时，C-FSW04模型max=14.886 32，max=3008 86；当=12°时，C-FSW04模型弹性变形量达到最大，分别提高约3.25%和4.13%。

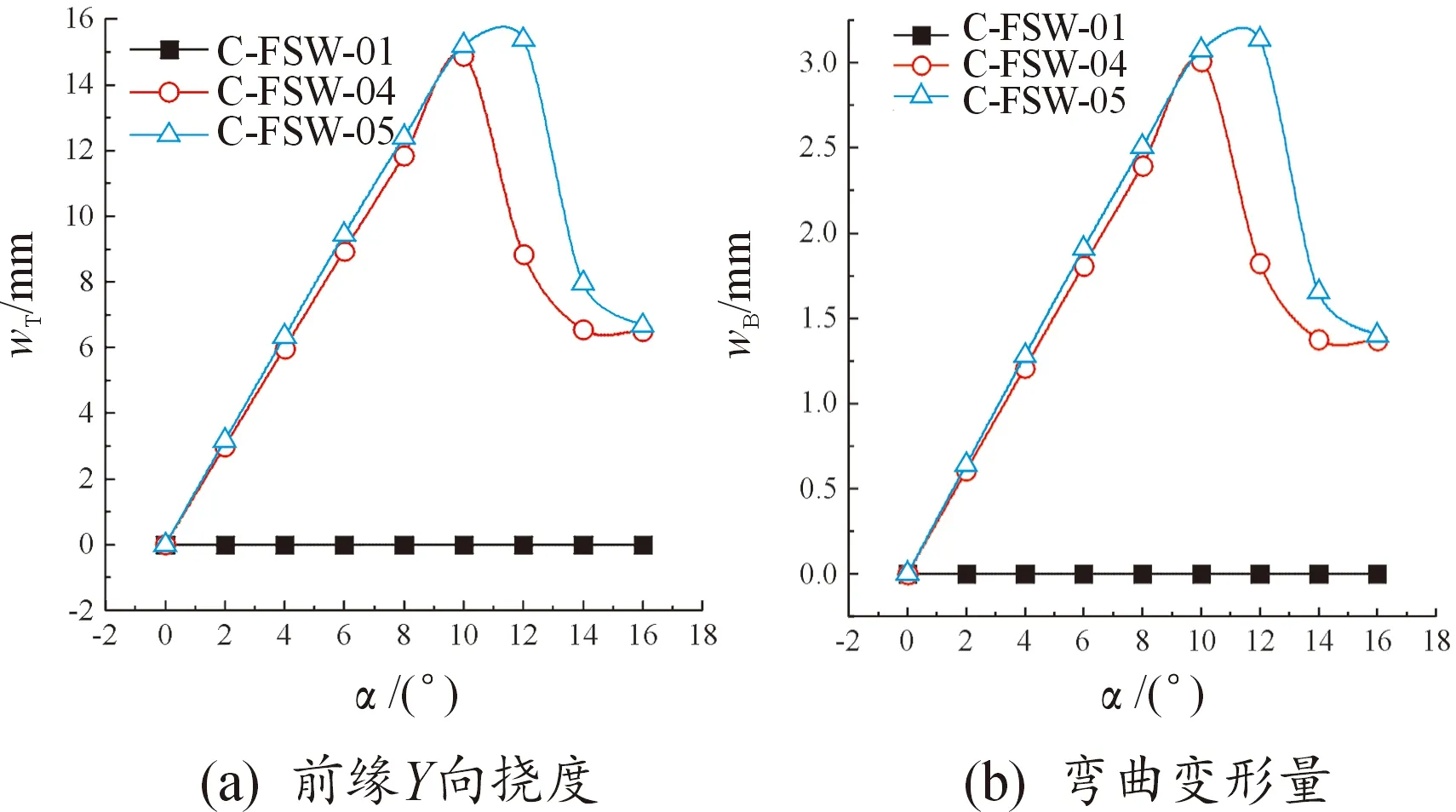
图14 主翼面弹性变形量曲线Fig.14 The elastic deformation characteristics of wing

5.3 流动机理分析

当=6°时，弹性条件下C-FSW01、C-FSW04和C-FSW05模型的流线图和压力云图如图15和图16所示。

图15 α = 6°时模型的流线图Fig.15 The streamline of different models when α = 6°

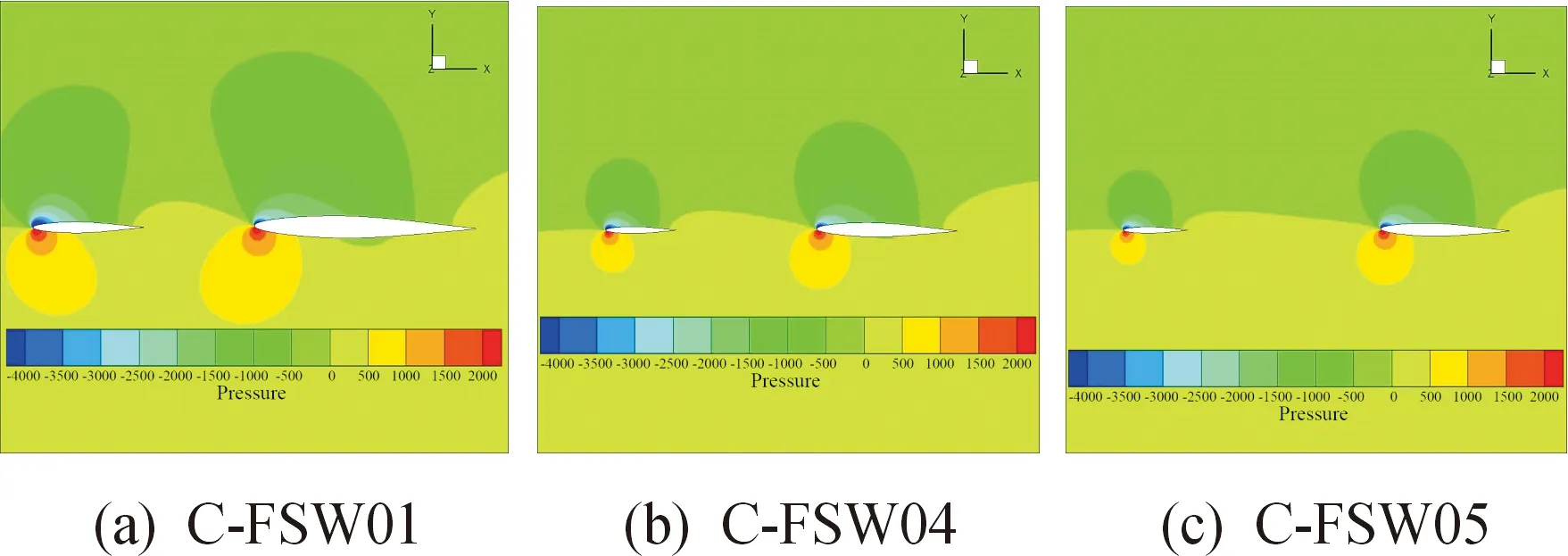
图16 α=6°时模型的压力云图Fig.16 The pressure contour of different models when α = 6°

由图15可知，在低马赫数、小迎角状态下，3种翼型均未出现明显气流分离，所以鸭翼对主翼的影响主要表现为扰流作用。由图16看出，3种模型表面压力差异不大。鸭翼与主翼距离增大，两者相互影响变小。远距鸭翼对主翼面的扰流作用减小，使远距鸭翼前缘上翼面流速更大，相较于其他模型气动特性更好。

当=12°时，弹性条件下C-FSW01、C-FSW04和C-FSW05模型的流线图和压力云图如图17和图18所示。

图17 α = 12°时模型的流线图Fig.17 The streamline of different models when α = 12°

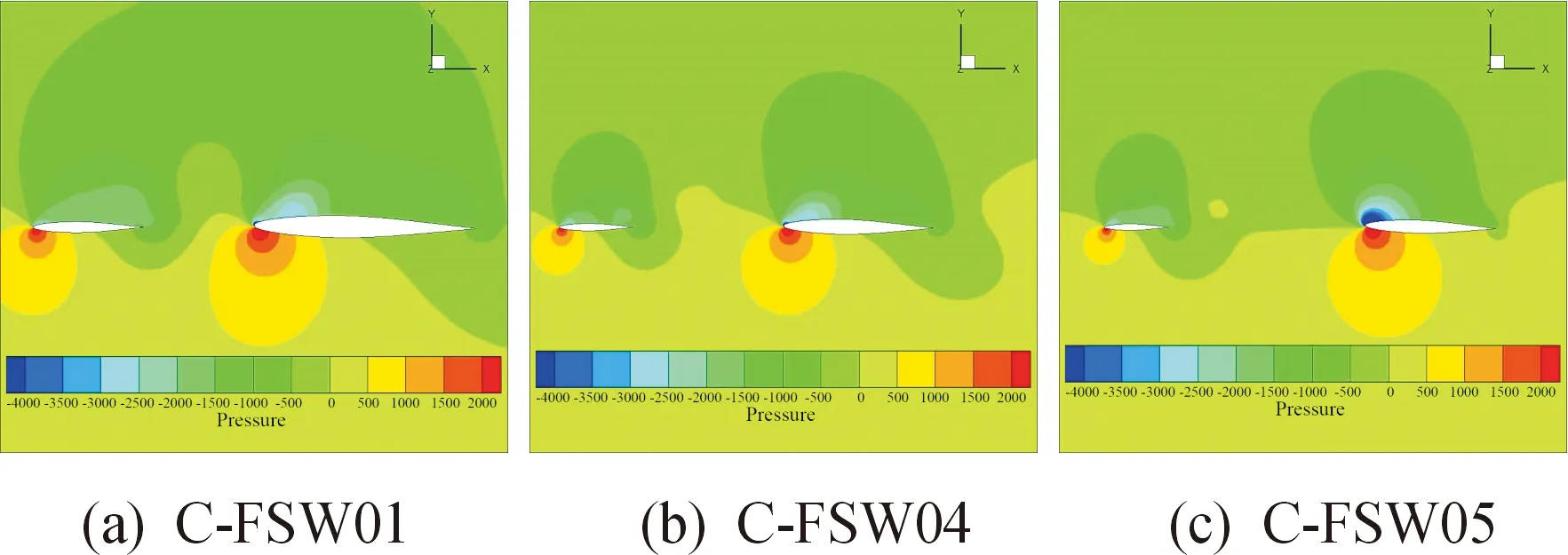
图18 α = 12°时模型的压力云图Fig.18 The pressure contour of different models when α = 12°

由图17和图18可知，当=12°时，3种模型翼型表面均出现明显的气流分离，上表面卷绕形成涡流，相比较于近距鸭翼模型，远距模型涡流明显减小。近距鸭翼主翼涡流与鸭翼涡的干扰作用明显，鸭翼涡对主翼涡的下洗作用导致主翼上表面气流提前分离，涡核破裂，上表面吸力减小主翼升力贡献减小，而主翼涡对鸭翼的上洗作用也减少了鸭翼有效迎角，延缓了鸭翼气流的过早分离，鸭翼上表面吸力增大，鸭翼升力贡献增大，但由于主翼是升力主要产生部件，所以远距鸭翼气动特性较好。

对于近距鸭翼模型，由于主翼涡形成较早，主翼涡翻卷较为严重，导致主翼上表面涡流不断向机翼前源扩散，旋涡区域气流流速下降，吸力减小，主要升力部件向前缘靠拢，由于主机翼刚心=055，所以气动中心与刚心距离逐渐变大，导致近距鸭翼升力分布变差，在上表面旋涡未覆盖整个上表面区域前(α<10°)，近距鸭翼模型弹性变形反而变大，同样压力贡献下比远距鸭翼模型变形量大。