基于在线参数辨识的变体飞行器控制

王子健,张书宇,侯明哲

(哈尔滨工业大学， 哈尔滨 150001)

1 引言

大多数飞行器具有固定的气动外形，这种固定气动外形的飞行器往往只能适应单一或少数几种飞行任务，但是变体飞行器能够在不同的飞行环境下，通过改变自身的外形从而提升飞行性能以满足不同的飞行任务需求，所以变体飞行器的控制问题是当前航空航天领域的热点问题之一。常见的变形方式可以按照变形尺寸概括为三类：小尺寸变形，如局部鼓包等方式改变飞行器的气动性能；中尺寸变形，如改变机翼的厚度等；大尺寸变形，如改变机翼翼展、后掠角等方式。其中大尺寸变形对飞行器的气动性能影响最大，所以相关研究也大多集中在这一领域。

目前大部分研究都集中于变体飞行器的变形-飞行协调控制问题，即飞行器变形过程中的稳定飞行控制或跟踪控制问题。文献[4]提出了一种抗饱和平滑切换控制策略，以解决飞行器变形过程中的姿态稳定控制问题。文献[5]针对可变后掠角飞行器建立了切换模型，研究了飞行器外形变化下的跟踪控制问题。文献[6-7]针对可变翼展与后掠角的变体飞行器建立了线性变形参数模型，设计了鲁棒增益调度控制策略保证了变形过程中的稳定性问题。

另一个研究方向则是将飞行器外形变化视作额外的控制输入，辅助传统的控制方式，最大程度的发挥变体飞行器的优势。文献[8]针对一种可变翼展高超声速导弹的变形辅助机动控制进行了研究，验证了将外形变化视作额外控制输入的优势。文献[9]将翼展视为额外控制输入，并将其解耦为速度、姿态、高度3个回路设计了滑模控制策略，提升了飞行器的机动性能与抗干扰性能。

变形辅助机动控制相比于变形-飞行协调控制能够在飞行器飞行过程中自主的调节外形以保证最优的气动外形，所以变形辅助机动控制的问题具有更大的意义。但是由于引入了变形辅助机动，飞行器将变成一个高度耦合的强非线性系统，而飞行器外形变化的方式也直接影响了飞行器模型的复杂程度。所以我们看到目前大部分研究仅关注外形单一变化飞行器的变形-飞行协调控制问题与变形辅助机动控制问题，而更为复杂的外形复合变化变体飞行器的变形辅助机动控制问题则鲜有涉及。

本文中以可对称改变翼展和后掠角的飞行器为研究对象，研讨了基于在线参数辨识的变体飞行器变形辅助机动控制问题。首先给出了可对称改变翼展和后掠角飞行器的动力学模型，接着基于此给出了变体飞行器的变形辅助机动控制模型。为简化控制器设计，将模型分为速度回路与姿态回路，设计了固定时间收敛的状态反馈控制策略。设计了一种在线时变参数辨识算法以针对外形变化导致的气动系数不确定性以及外界扰动对飞行器的影响进行辨识。然后通过控制分配保证得到的控制指令能够合理的分配给控制输入。最后通过仿真验证了本文中提出方案的有效性。

2 面向控制的变体飞行器变形辅助机动控制模型

本文中采用Navion L-17飞机为飞行器本体，两侧翼展与后掠角能够对称变化的变体飞行器为研究对象。定义机翼翼展的变化范围是原翼展到2倍翼展，机翼后掠角的变化范围为0～40°。

变翼展变后掠角飞行器面向控制的纵向模型可以表述为如下形式：

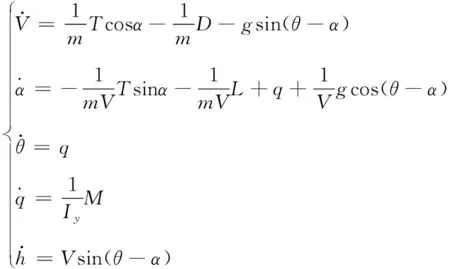
(1)

式中：为速度；为俯仰角；为俯仰角速度；为飞行器质量；为飞行器绕轴转动惯量；为高度；为油门开度；为推力且推力可表述为下式 ：

=

(2)

式中：=413 N/%为推力系数；为油门开度。

升力，阻力以及俯仰力矩满足如下关系：

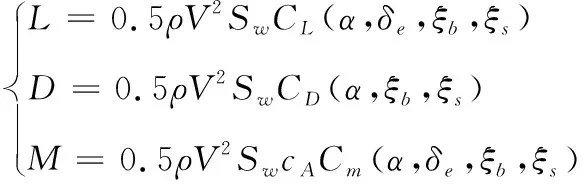
(3)

式中：、、分别为空气动力产生的升力、阻力以及俯仰力矩；为空气密度；为机翼参考面积；为平均几何弦长；为翼展变形率；后掠角变形率分别定义如下：

(4)

式中，为翼展；和分别为飞行器无形变时的翼展以及最大形变时的翼展,且∈[0,1]；为后掠角；和分别为飞行器无形变时的后掠角以及最大形变时的后掠角,且∈[0,1]。升力系数，阻力系数，俯仰力矩系数函数关系定义如下：

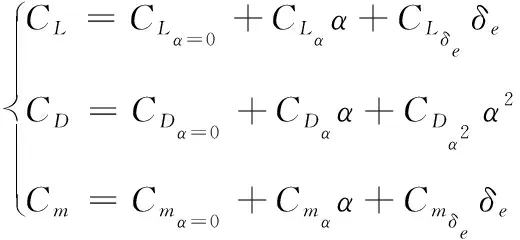
(5)

式中：为迎角；为升降舵偏角；=0320 9，=-1019 9，其余气动导数与零迎角时的气动系数整理成如下矩阵形式：

[=0=0=0]=[1]

(6)

其中，矩阵系数为：

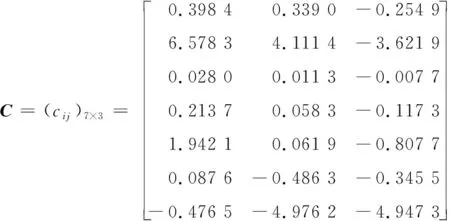
(7)

将翼展变形率，后掠角变形率视为额外的控制输入，得到如下模型：

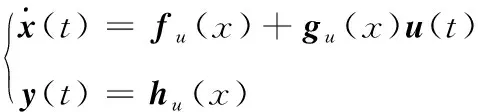
(8)

式中：()=[]为状态向量；()=[]为输入向量；()=()=[]为输出向量。

系统函数()定义如下：

()=[1()2()3()4()5()]

(9)

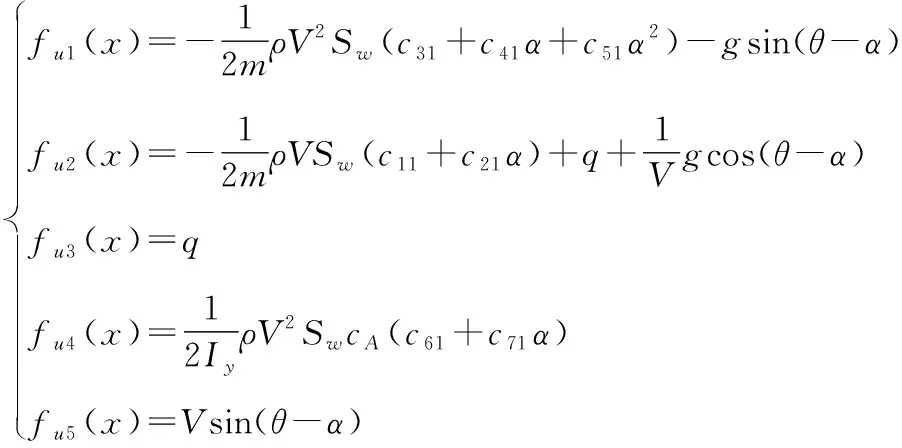
系统函数()定义如下：

()=[()],=1,2,3,4

()=[()],=1,2,3,4,5

(10)

其中

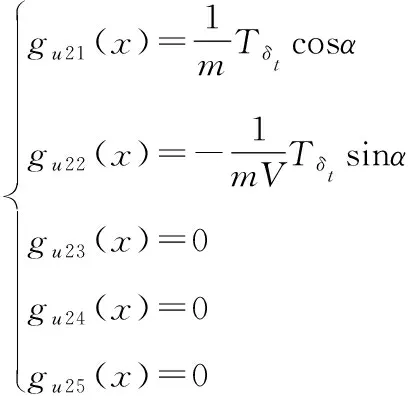
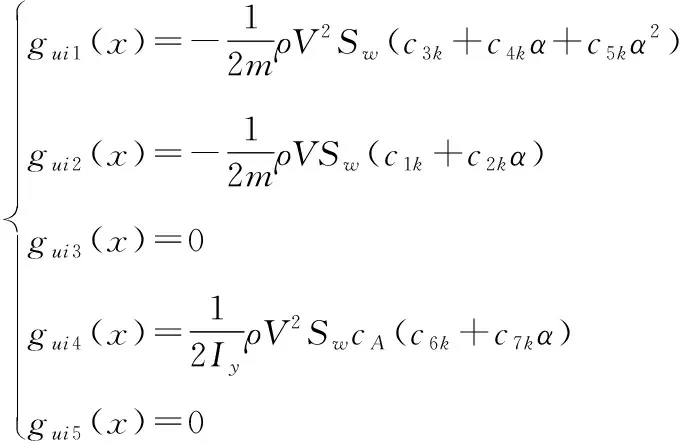
=-1,=3,4

此时可变翼展和后掠角的变体飞行器的变形辅助机动控制模型简化为一个仿射非线性模型，考虑外形变化导致的气动系数不确定性和外界扰动对模型的影响将上述模型分为速度回路和姿态回路并给出相对应的含有待辨识参数的形式。速度回路由下式给出：

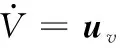
(11)

其中，=1+[1]+Δ1Δ31+Δ41,=1,2,3,4, Δ1、 Δ31、 Δ41为待辨识参数。

飞行器的高度由飞行器的姿态通过跟踪PID算法得到的进行控制，飞行器的姿态回路由下式给出：

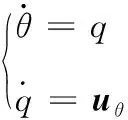
(12)

其中,=4+[4]+Δ4Δ34+Δ44,=1,2,3,4,Δ4、 Δ34、 Δ44为待辨识参数。

3 变体飞行器的变形辅助机动控制

3.1 控制器设计

为了保证飞行器的跟踪性能，这里我们选用一类固定时间收敛的状态反馈控制器，控制器的具体设计方案可见文献[10]，得到速度回路与姿态回路的控制器如下：

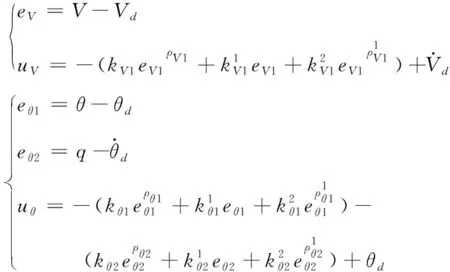
(13)

3.2 在线时变参数辨识算法设计

为了得到待辨识参数，以姿态回路为例，首先构造带有时变参数的非线性系统：

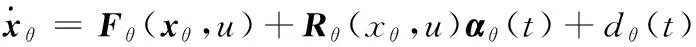
(14)

其中，=[]是状态向量；()=[Δ4Δ34Δ44]为待辨识参数；()为外界的噪声以及干扰。已知非线性函数(,)和已知回归矩阵(,)如下所示：

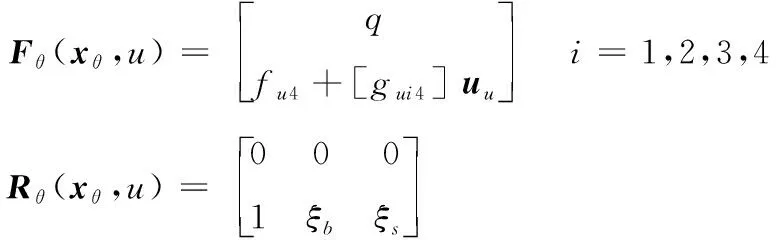
(15)

假设状态，输入，未知扰动()，未知参数向量()的导数均有界，(,)与(,)均为和的连续有界函数。

为了得到未知参数向量()与可测或已知变量之间的关系，构造如下滤波器：

(16)

其中，是滤波系数，由上述假设可知，有界并设<,>0。

通过式(16)提出的滤波器作用于系统(14)有：

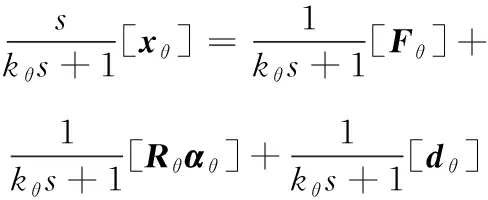
(17)

结合式(16)和(17)并针对(1+1)[]应用交换引理，可以得到：

+-

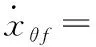
(18)

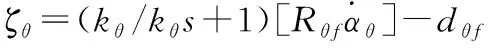
于是我们得到了未知参数向量()与已知变量、、、之间的关系，为了基于这个关系设计自适应律，首先给出如下中间回归矩阵以及中间向量：

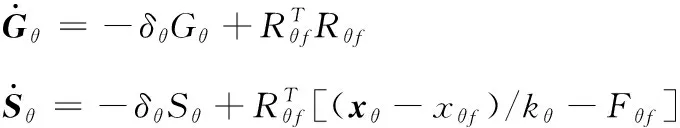
(19)

其中，(0)=0,(0)=0,为大于0的常数，矩阵为正定矩阵。

定义辅助向量1、2如下：

(20)

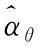
将式(19)中的中间回归矩阵与中间向量代入到式(20)中的辅助向量中，能够得到下式：

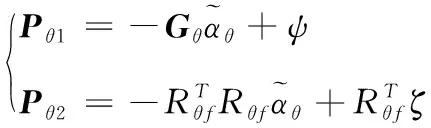
(21)

设计估计参数自适应律如下：

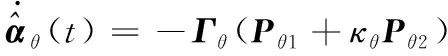
(22)

其中，>0为定常对角学习增益矩阵；>0为正常数，用来平衡快速辨识参数的能力和算法的鲁棒性，自适应律的收敛性在文献[]给出了说明。

3.3 控制分配

为了合理地将得到的控制信号[]分配到控制输入()=[]中去，需要满足

=

(23)

其中，

(24)

在进行控制分配的时候我们希望控制输入在工作点附近变化幅度尽可能小，同时也希望执行器对执行器变化速率进行优化，于是将控制分配问题描述为如下形式：

(25)

其中：、为正定的对角权值矩阵；是飞行器平稳飞行的工作点；为数字控制系统的采样时间。

控制分配式(25)的解为：

=+

(26)

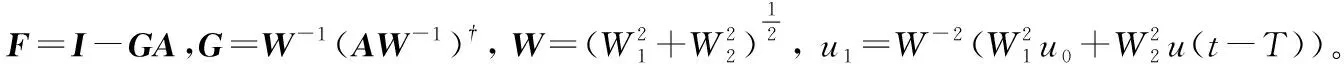
4 仿真验证

设定飞行指令如下：初始时，飞行器在5 000 m高度以50 m/s的速度匀速飞行，从20 s开始，开始改变飞行的速度与高度；在第50 s时，飞行速度达到60 m/s后保持；第70 s时，飞行器开始减速；80 s时，飞行器达到最低高度4 900 m并保持；第90 s时，飞行器减速到50 m/s并保持现有速度与高度继续飞行。

在飞行过程中，对飞行器施加20%的气动系数不确定性以及1 000 N·m的俯仰力矩干扰，其周期均为60 s。变体飞行器的物理参数为：=1 247 kg;=17.1 m;=1.737 m;=4 067.45 kg·m;=1.055 5 kg/m。

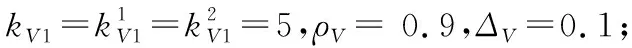
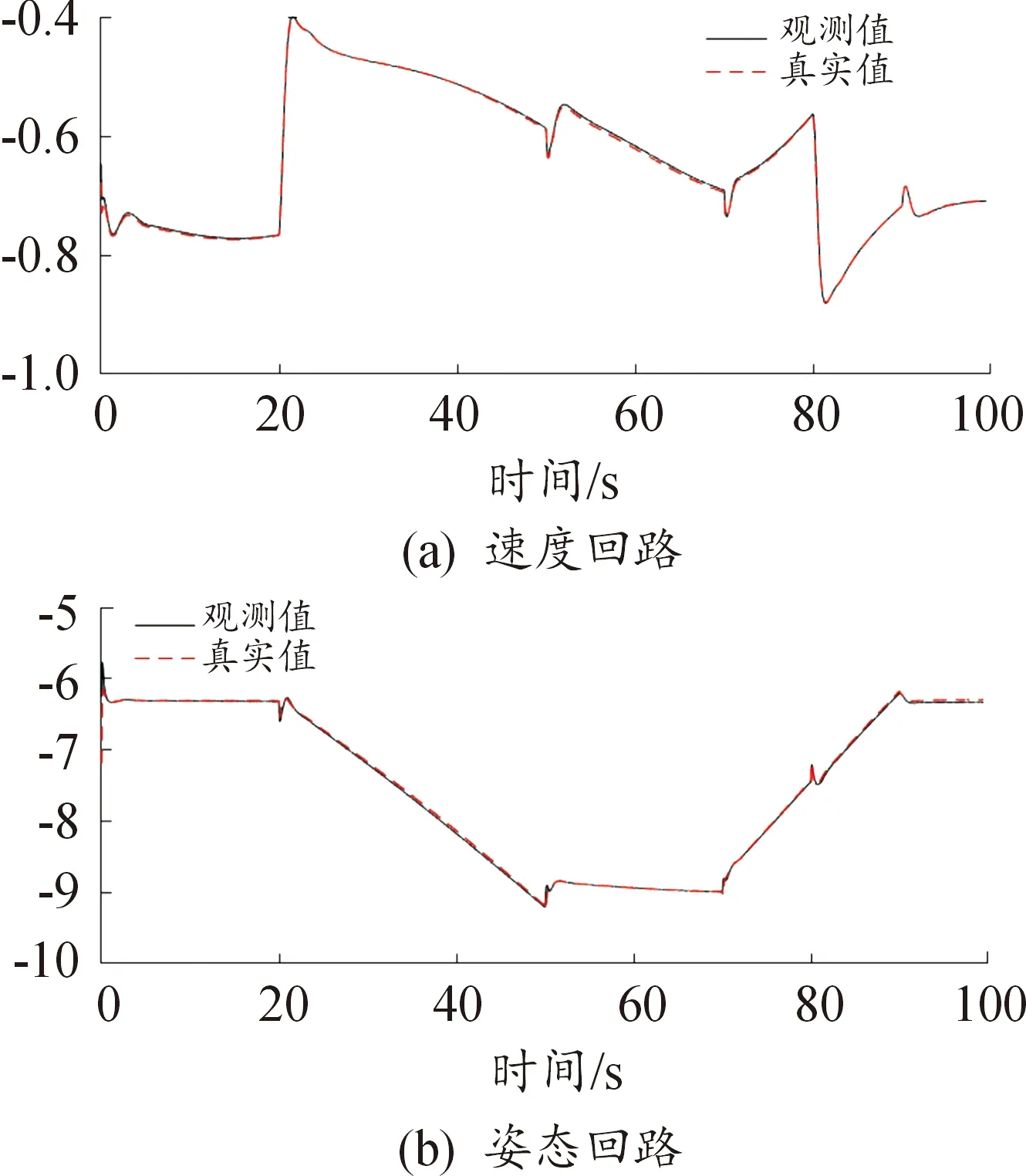
图1 参数辨识结果曲线

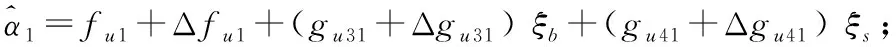
仿真结果如图2所示。

从仿真结果我们可以看出，本文中提出的在线时变参数辨识在具有外形变化、气动系数不确定性和外界扰动的情况下很好的辨识出了真值，并结合控制器与控制分配策略达到了预期的控制效果。

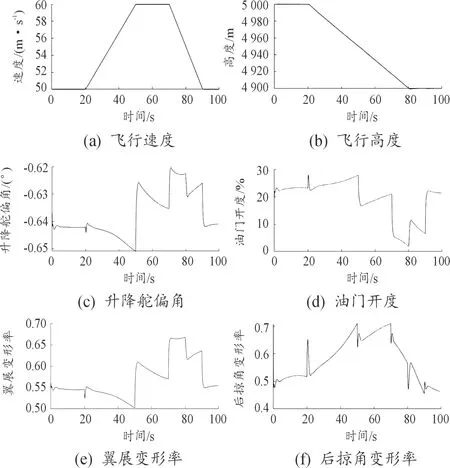
图2 仿真结果曲线

5 结论

本文中以可变翼展变后掠角的变体飞行器为对象，建立了变体飞行器变形辅助机动控制模型。设计了基于交换引理的在线参数辨识自适应律、固定时间收敛的状态反馈控制器和基于在线参数辨识的控制分配算法。仿真结果表明，在线时变参数辨识可以精确辨识出气动系数不确定性以及外界干扰对飞行器模型的影响，基于此设计的控制器和控制分配方案达到了预期的控制效果。