基于蒙特卡洛方法的邮船建造质量评价体系不确定性分析
2022-10-31丁东宇姚汝林汪学锋
丁东宇, 姚汝林, 毛 锐, 汪学锋, 余 龙*
(1.上海交通大学 a.海洋工程国家重点实验室; b.高新船舶与深海开发装备协同创新中心;c.船舶海洋与建筑工程学院,上海 200240;2.招商局邮轮制造有限公司,江苏 南通 226116)
0 引 言
船舶建造项目具有投资规模大、设备及原材料种类多、建造周期长、工序复杂、劳动力密集等特点,一旦建造质量出现问题,返工成本较高,会对船厂和船舶所有人造成巨大损失。在众多船型中,豪华邮船被誉为世界造船业皇冠上的明珠,被国际船舶业公认为技术含量高、附加值高、可靠性高的“三高”船舶[1],除满足基本性能外,还需要考虑舒适性、游客便捷性和娱乐设施丰富性等。相比其他船型,豪华邮船的建造过程更复杂,在内装过程中需要的材料和设备数量大、种类多[2],特别需要对建造质量进行控制,防止由建造质量问题引起的后续返工。
国内外学者对船舶建造质量评价体系有一定的研究。周宏等[3]根据潜艇建造的生产特点和可靠性理论建立潜艇建造质量评价参数体系。陈新飚[4]采用总目标逐层分析法建立船舶建造质量评价体系,并开发软件投入工程应用。刘曼婷[5]使用数据挖掘方法,分析船舶建造过程中的关键评价指标,建立质量评价模型。虽然国内对船舶建造质量评价有一定的研究,但系统性的研究较少,往往只针对建造过程中某个单独环节进行分析,且针对邮船建造质量评价体系的研究鲜有出现。BUKSA等[6]通过失效模式和效应分析方法进行船舶管道生产质量分析,并利用Ishikawa图和品率控制图定性分析过程的关键输入变量。PARK等[7]通过将过程挖掘和数据包络分析相结合的系统化方法对船体分段生产计划进行评估,为改善造船效率提供指导方针。国外研究主要集中在可靠性、造船效率和造船精度等方面,对质量评价体系的研究较少。随着中国邮船设计建造迈入实质性实施阶段,需要对邮船建造质量评价体系进行研究,弥补国内市场空白。
建立邮船建造质量评价体系的结构和数学模型,各部分的权重可通过层次分析法(Analytic Hierarchy Process,AHP)或德尔菲法确定,并使用蒙特卡洛方法对该体系的不确定性进行研究。
1 质量评价对象
1.1 评价体系结构
船舶是由船体、舾装、推进系统、电力系统、通信系统、导航系统等组成的复杂大型系统[8],邮船又是一种具有多层甲板结构的复杂船型,其上层建筑使邮船的设计和建造难度激增,远超普通船型。建造过程所用的原材料和配套件品种多,导致质量管理的对象多,流程复杂,质量管理难度大。
采用总目标逐层分析法[4],应用船舶工程分解结构(Ship Work Breakdown Structure, SWBS)[8]概念将邮船建造过程中多层次的复杂问题进行逐层分析,将复杂问题简化处理。如图1所示:邮船建造质量评价体系由一级评价部分、二级评价部分、三级评价部分和评价参数共4个层次组成,评价部分和评价参数按照GB/T 34000—2016《中国造船质量标准》确定。一级评价部分包括船体建造质量、船装质量、机装质量、电装质量、涂装质量、内装质量、系泊及航行试验质量和完工交船质量。每个一级评价部分由若干个二级评价部分组成,每个二级评价部分由若干个三级评价部分组成,每个三级评价部分又由若干个评价参数组成。

图1 邮船建造质量评价体系结构
1.2 评价体系数学模型

Ai=AWi
(1)
Aij=AiWij
(2)
Aijk=AijWijk
(3)

Aijkl=AijkRijkl
(4)
评价参数的得分值Sijkl是在Aijkl的基础上再乘以评价参数函数Pijkl(αijkl),其中:αijkl为某评价参数的实际结果;Pijkl为评价参数函数的评分标准。显然Pijkl(αijkl)≤1,则某项评价参数的得分值为
Sijkl=AijklPijkl(αijkl)
(5)
由式(1)~式(5)可得到某项评价参数的得分值公式:
Sijkl=AWiWijWijkRijklPijkl(αijkl)
(6)
将质量评价体系中的每一个评价参数得分累加,可得到各个评价部分的得分总值和质量评价体系的得分总值:
(7)
(8)
(9)
(10)
由上述分析可知:仅研究一级、二级、三级评价部分的权重、评价参数的权重和评价参数函数的评分标准即可求得质量评价体系的得分总值。
2 质量评价方法研究
完成邮船建造质量评价体系数学模型的建立,还需要得到一级、二级、三级评价部分和评价参数的权重,可使用AHP或德尔菲法。
2.1 AHP
AHP是应用较广泛的多准则决策工具[9],自发明以来已在许多领域得到广泛的应用。AHP可灵活地与线性规划、质量函数展开、模糊逻辑等不同的技术相结合,有效处理变量之间的关联性和独立性,利用矩阵特征值和特征向量进行群组判断,以确定某些变量的赋值,有助于在决策中整合群体共识[10]。
2.1.1 基本原理
假设有n个变量需要赋值,可两两取比值,构造一个n阶方阵,称为判断矩阵:
(11)
式中:aij>0;aii=1;aij=1/aji;aij=aikakj。
矩阵A′乘以向量W=(w1w2…wn)T得:
(12)
由矩阵原理可知:判断矩阵A′的最大特征值等于其阶数,即λmax=n,式(12)可化为
A′W=λmaxW
(13)
通过该方法,可将变量赋值问题转变为矩阵运算问题,但判断矩阵的构造具有试探性,后续需要进行一致性检验确保其合理性。
2.1.2 应用步骤
应用AHP解决质量评价问题,大体分为4个步骤:(1)针对评价目标建立清晰的递阶层次结构;(2)构造判断矩阵;(3)对判断矩阵进行一致性检验;(4)计算特征向量,得到评价值。
2.2 德尔菲法
德尔菲法由美国兰德公司提出,由主持机构以书面形式征询专家们的意见,再对专家意见进行统计整理,得到最终结果[11]。该方法的优点是匿名性,得到的统计结果不受个人权威、资历等问题的影响,便于专家们充分发表观点。
3 基于蒙特卡洛方法的质量评价体系不确定性研究
由于不同船厂对邮船建造质量评价体系会有不同的理解,或是应用于不同类型的邮船,体系的权重会有所不同,因此该体系存在不确定性。邮船建造质量评价的过程可用下式表示:
A″B=C
(14)
式中:A″为质量评价体系;B为各评价部分的得分;C为得分总值。
由于该体系的不确定性较难量化,且有随机性,因此使用蒙特卡洛方法[12]分两部分研究邮船建造质量评价体系的不确定性,包括不同船厂在使用该体系时的不确定性和同一船厂针对不同船型使用该体系时的不确定性。
3.1 质量评价体系应用于不同船厂时的不确定性
由于国内邮船建造正处于起步阶段,相关资料较少,无法通过大量资料总结得出邮船建造质量评价体系评价部分和评价参数的权重,因此利用随机数方法产生各评价部分和评价参数的重要度得分,得到各评价部分和评价参数的权重,再使用蒙特卡洛方法大量重复这一过程,得到同一艘邮船在不同权重下的质量评价及其分布区间,对应不同船厂在使用该体系时的不确定性。
针对每个评价部分和评价参数,生成1个随机数表示其重要程度,随机数范围为1~5,数值越大,其重要程度越高。
假设第k个三级评价部分有p个评价参数,分别生成p个随机数aijk1,aijk2, … ,aijkp,则可得到评价参数权重:
(15)
假设第j个二级评价部分有q个三级评价部分,分别生成q个随机数aij1,aij2, … ,aijq,则可得到三级评价部分权重:
(16)
一级评价部分权重和二级评价部分权重同理可得。评分标准如表1所示。

表1 评价参数函数的评分标准
在利用随机数方法得到权重的过程中,采用均匀分布随机整数、均匀分布随机数和正态分布随机数等3种随机数生成方法,其中:均匀分布随机整数可用于模拟实际问卷的情况。使用MATLAB软件重复上述过程100 000次,再对同一艘邮船进行质量评价,得到同一艘邮船在不同权重下的质量评价得分及其分布区间,如图2所示。

图2 某邮船不同权重下的质量评价得分及其分布区间
通过问卷的形式得到某业内专家给出的权重,与上述结果进行比较,如表2所示。由表2可知:3种随机数生成方法得到的质量评价得分的均值和中位数基本相等,正态分布随机数的标准差最小,且最终得分均呈正态分布,与通过问卷形式得到的结果相差不大。

表2 某邮船不同权重下的质量评价得分
针对邮船特点,选取内装质量部分,对某邮船的初步建造质量进行评价,该部分质量评价体系如表3所示。

表3 内装质量部分评价体系
同样使用蒙特卡洛方法得到某邮船在不同权重下的内装质量评价得分及其分布区间,如图3所示。表4为某邮船不同权重下的内装质量评价得分。由表4可知:3种随机数生成方法得到的质量评价得分的均值和中位数基本相等,正态分布随机数的标准差最小,且最终得分均呈正态分布。图4为该邮船几种典型的内装质量问题,在评价体系中分别对应“缺钉情况”“隔热绝缘”“敷料表面平整度”“地毯表面无破损”等评价参数,该部分评价为略低于或远低于质量考核要求。针对这些典型问题,分别将对应评价参数的得分值设为最高和最低,再使用蒙特卡洛方法得到内装部分质量评价得分均值(正态分布随机数),比较其对内装质量的影响。表5为内装质量典型问题对应评价参数对内装质量的影响。由表5可知:“敷料表面平整度”和“隔热绝缘”的影响较大。
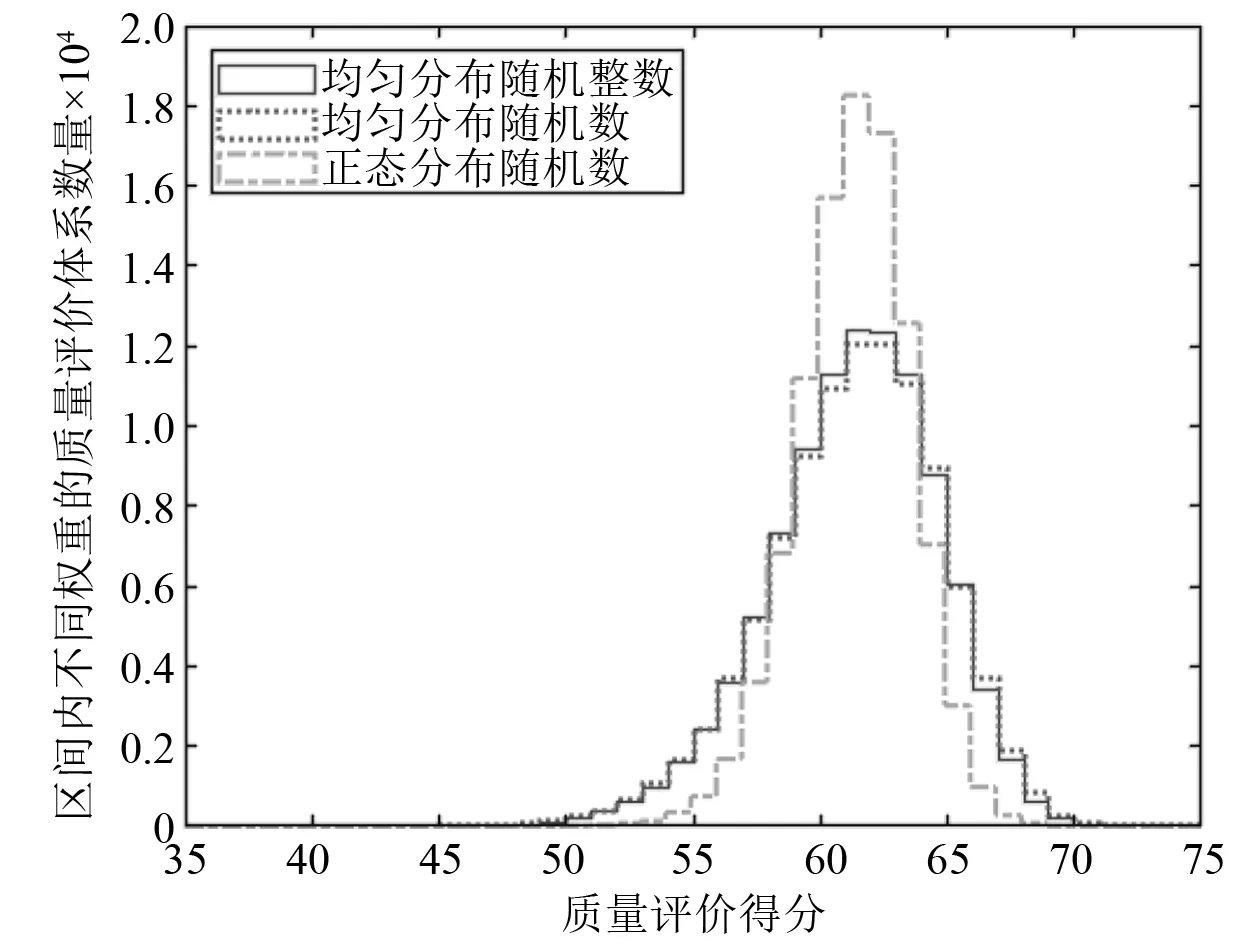
图3 某邮船不同权重下的内装质量评价得分及其分布区间

表4 某邮船不同权重下的内装质量评价得分
3.2 质量评价体系应用于不同船型时的不确定性
将该质量评价体系应用于内装部分较少的船舶(如散货船等),再与应用于邮船的结果进行比较。利用随机数方法生成各评价部分的得分,再使用蒙特卡洛方法大量重复这一过程,得到不同类型船舶在同一套质量评价体系(权重相同)下的质量评价得分及其分布区间,如图5和图6所示。

图4 内装质量典型问题

表5 内装质量典型问题对应评价参数对内装质量的影响

图5 不同邮船质量评价得分及其分布区间(权重相同)

图6 不同散货船质量评价得分及其分布区间(权重相同)
表6为邮船和散货船的质量评价得分。由表6可知:3种随机数生成方法得到的质量评价得分的均值和中位数基本相等,均匀分布随机数的标准差最小,且最终得分均呈正态分布。邮船内装质量部分占比约25%,散货船约11%,在一定程度上说明邮船内装的重要程度。

表6 邮船和散货船的质量评价得分
4 结 论
(1)邮船建造质量评价是一个复杂体系,建立邮船建造质量评价体系的结构和数学模型,评价过程由各评价部分及评价参数决定,可使用AHP或德尔菲法确定各评价部分和评价参数的权重,得到一套客观合理的邮船建造质量评价体系。
(2)由蒙特卡洛方法的结果可知:质量评价得分的均值和中位数基本相等,且最终得分均呈正态分布,说明该体系具有较好的稳健性。
(3)不同船厂对邮船建造质量评价的理解和认识往往不同,使用该体系需要注意其不确定性,应结合船厂实际情况,考虑船厂的长处和短板,调整相应的权重。
(4)邮船相比其他船舶,由于内装质量部分占比较高,相对重要许多,因此在建立体系时尤其需要注意内装质量部分的权重。
