前置式滚筒洗衣机驱动轴系统设计

朱甫金

滚筒洗衣机在脱水过程中不可避免的存在偏心负载，高速脱水产生的离心力导致滚筒悬挂系统产生振动，使滚筒驱动轴系统承受复杂的荷载。近年来，超薄、大直径滚筒、高转速已成为滚筒洗衣机产品的发展趋势，对滚筒洗衣机驱动轴系统的设计要求日益严苛。虽然有限元分析技术可以在设计方案完成后进行轴系统强度分析，但在设计一款全新产品时，要求满足最紧凑深度尺寸、最优材料成本，就必须在设计方案阶段确定滚筒驱动轴系统的轴承跨距、轴承型号以及主轴直径，量化计算轴承寿命和主轴疲劳强度，避免洗衣机寿命试验过程中发生轴承失效、主轴疲劳断裂的重大质量问题，满足滚筒洗衣机可靠性设计目标。

本文应用动静法原理[1]，对前置式滚筒洗衣机脱水过程中驱动轴系统的受力进行仔细分析，计入了以往文献[2]、[3]、[4]中遗漏的滚筒悬挂系统振动产生的惯性力负载，将偏心负载产生的离心力和振动惯性力叠加，作为前置式滚筒洗衣机悬臂梁结构驱动轴系统的真实负载，进行轴承的选型和寿命计算、主轴的疲劳强度计算，并按照疲劳损伤累积理论对轴承寿命、主轴疲劳应力计算进行了详细介绍，作为滚筒洗衣机设计、试验的参考。

1 驱动轴系统受力分析

滚筒洗衣机在脱水过程中，偏心衣物负载将产生离心力从而引起滚筒悬挂系统强迫振动。如果把摩擦减振器的阻尼力、门封橡胶阻尼力等效为线性阻尼，滚筒悬挂系统在垂直面内的刚体运动可简化为简谐运动，离心力Fcnt激扰的垂直方向y 振幅为[5]：

式中：Y为振幅，ω为圆频率，ψ为振动相位角。在水平方向x，也有相似的强迫振动，只是两个方向的刚度、阻尼有差异，振幅、相位角不同。

离心力引起的强迫振动，将产生惯性力，如图1 所示，滚筒转动系统垂直方向的惯性力幅值为：

图1 滚筒受力

式中：M为包含脱水衣物质量在内的滚筒转动系统质量，ω为滚筒脱水转速的角速度，Y为振动幅值。

应用动静法原理对滚筒悬挂系统进行受力分析，很显然，对于悬臂支承的滚筒转轴系统，三脚架、主轴、轴承在脱水过程中承载的不仅仅是偏心衣物产生的离心力，还承载了振动产生的惯性力。笔者看到过的多份公司内部有限元分析报告，和类似于[2]、[3]、[4]公开文献中，在轴承寿命计算、结构强度分析中都忽略了第二部分惯性载荷，只考虑了离心力负载。在下面的受力计算中可以看到由此产生的误差是很大的。

2 滚筒洗衣机脱水过程偏心负载的概率分布

现在的滚筒洗衣机都采取变频电机驱动，变频器驱动算法可以准确地判断筒内衣物负载的大小、衣物偏心量的大小，甚至可以检测偏心质量在滚筒轴向的位置。洗衣控制软件的脱水算法设计，都对衣物负载量、偏心大小进行分档，选择满足洗衣机结构强度的转速进行脱水运转。

为了计算滚筒驱动轴系统的载荷，必须明确洗衣机在用户家庭使用寿命周期内发生的偏心负载大小的频度分布。表1 为一款BLDC 电机驱动、64 L 滚筒容积洗衣机模拟家庭衣物负载的脱水偏心量频度分布。衣物负载组成为：大浴巾、牛仔裤、衬衣、T 恤、厚茄克、床上四件套、厚窗帘，以及它们的组合，干衣组合重量从0.5 kg 到7 kg，共28 种组合。运行漂洗+脱水程序，每种负载组合进行12 次脱水偏心检测，记录400 rpm 预脱水后进入主脱水前的偏心检测值。考虑到最终脱水的偏心量控制在1.2 kg 以下，记录数据剔除了超过1.2 kg偏心值。

参考表1 偏心量分布频度，结合洗衣机软件脱水算法对偏心量的分级，将脱水偏心量合并简化为表2 分布频度作为轴系统变载荷计算的偏心量。

表1 336 次不同家庭衣物脱水偏心量频度分布

表2 脱水偏心量简化分布频度

3 轴承载荷计算和选型

上文提到滚筒轴系统承载了偏心衣物产生的离心力以及振动产生的惯性力。滚筒悬挂系统的强迫振动幅度不仅与衣物偏心量有关，也与悬挂系统的设计参数、重心配置密切相关。表3 为一款64 L/1 400 rpm 滚筒洗衣机空筒负载、中间放置0.5 kg 橡胶偏心测得的振动加速度。

滚筒悬挂系统可近似为线性系统，不同偏心量的振动加速度可按表3 的测量值按比例计算；并且假设悬挂系统水平、垂直方向的振动相位相同，由此可计算脱水过程中滚筒转动系统的惯性力：

表3 0.5 kg 偏心激励的悬挂系统振动加速度（单位：g）

按图2 所示悬臂梁支承的滚筒轴系统尺寸，计算大轴承A、小轴承B 承受的载荷：

图2 轴承受力

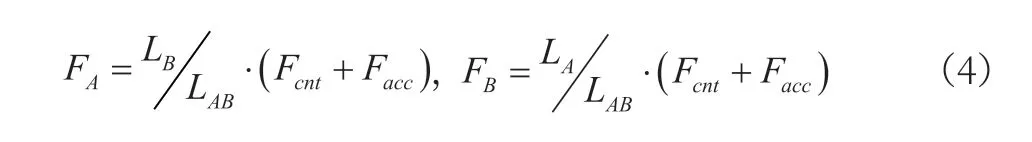
洗衣机脱水过程中轴承承受不稳定载荷和不稳定转速，轴承的寿命可按照不稳定变应力疲劳损伤累积理论进行计算[6]，深沟球轴承计算载荷为：

式中：Fi为对应第i偏心、转速的轴承受力；ni为洗衣机设计寿命周期所对应的第i偏心、转速的脱水转动圈数；nsum=∑ni是洗衣机设计寿命周期总的脱水转动圈数。

对应洗衣机设计寿命周期的轴承寿命系数为：

式中：C为轴承额定动载荷，可由轴承手册查得。

为了保证滚筒洗衣机在设计寿命周期内（如2 500 周期）轴承不发生失效，根据式（6）计算得到的寿命系数应该大于1。由于外侧小轴承B 的散热条件优于内侧大轴承A，根据多年的寿命测试经验，如果受到成本、结构尺寸限制，小轴承B 的寿命系数可略微小于1，但大轴承的寿命系数必须得到保证。

计算轴承寿命系数时，按照洗衣机运行一个标准程序的脱水转速曲线、脱水降档控制，结合表2 脱水偏心量分布频度，汇集成表4 所示偏心量、转速、脱水时间、运转周期数据。

上述这款洗衣机选择6306/6305 深沟球轴承，轴承跨距LAB=68.5 mm。滚筒转动系统质量6.5 kg，脱水时衣物负载按15 kg 计算。带负载脱水时悬挂系统振动加速度略小于空筒情形，结构受力分析时近似按照表3 空筒加速度测量值。利用表4 参数和式（5）、（6）可计算得到轴承A、B 的计算载荷Fm,A=6 825 N，Fm,B=4 709 N，洗衣机2 500 寿命周期脱水总转数nsum=23.5x106，轴承寿命系数为Lbearing,A=2.64，Lbearing,B=4.46，轴承设计寿命有足够余量。

表4 一款64 L/1 400 rpm 滚筒洗衣机脱水控制参数

如果选择轻型系列6206/6205 轴承，相应的寿命系数为0.99、1.12，洗衣机使用寿命设计目标是有风险的。顺便指出，如果只考虑脱水过程中偏心的离心力载荷，忽略振动产生的惯性载荷，6306/6305 轴承的计算寿命系数为11.6、19.8，洗衣机2 500 周期的轴承寿命估算差距4.5 倍，惯性力负载对轴承寿命计算的影响是非常大的。

4 主轴的疲劳寿命估算

滚筒洗衣机脱水过程中，主轴承受的弯曲应力由偏心衣物的离心力和滚筒悬挂系统振动产生的惯性力组成。离心力方向随转轴一起旋转，在主轴上产生的弯曲应力不变；而振动产生的惯性力随时间作周期性变化，在旋转轴上产生交变应力。因此，洗衣机主轴承受的是不对称交变应力，其应力循环特征为：

式中，σm,i、σa,i为第i偏心、转速的离心力产生的平均应力、惯性力产生的应力幅。理论上悬挂系统的受迫振动加速度与脱水转速不是平方关系，因此应力循环特征不是恒定值。将不对称变幅循环应力转化为对称循环应力幅[7]：

式中：Kσ为理论应力集中系数，ε为零件尺寸因数，β为零件表面质量因素，ψσ为折算系数，碳钢受弯曲应力一般取值0.2。这些系数可从工程手册或文献[7]、[8]查阅。

主轴承受非对称不稳定单向弯曲应力，疲劳强度按照线性疲劳损伤累积理论（Miner 法则）进行计算，累积疲劳的计算应力为[6,7]：

式中：m为材料常数，钢材m=9；N0=107 为材料疲劳极限寿命。

主轴疲劳强度的计算安全系数：

式中：σ-1为材料耐久疲劳限，45 号碳钢调质处理，σ-1=294 MPa。疲劳强度安全系数一般取[6]1.5～1.8。

洗衣机主轴的非对称循环应力特征r〉0,因此还需要按最大应力值校核静强度[8]。

上述这款洗衣机的主轴如图3 a），疲劳应力的危险截面为前端环槽位置E，弯矩图如图3 b）。材料为45 号钢调质，环槽处应力集中系数[7]Kσ=2.1，零件尺寸因数ε=0.91，零件表面质量因素β=0.95。按照表4 列出的洗衣机脱水控制参数，可得到累积疲劳的计算应力σca=142 MPa，安全系数Sca=2.1，满足设计寿命要求；另外，在960 rpm、0.8 kg 偏心脱水时应力特征r=0.23，最大应力σmax=155 MPa，与45号钢的屈服应力483 MPa 还有很大安全余量。大轴承A 左侧的台阶处，弯矩更大，一般来说也应该校核疲劳强度。

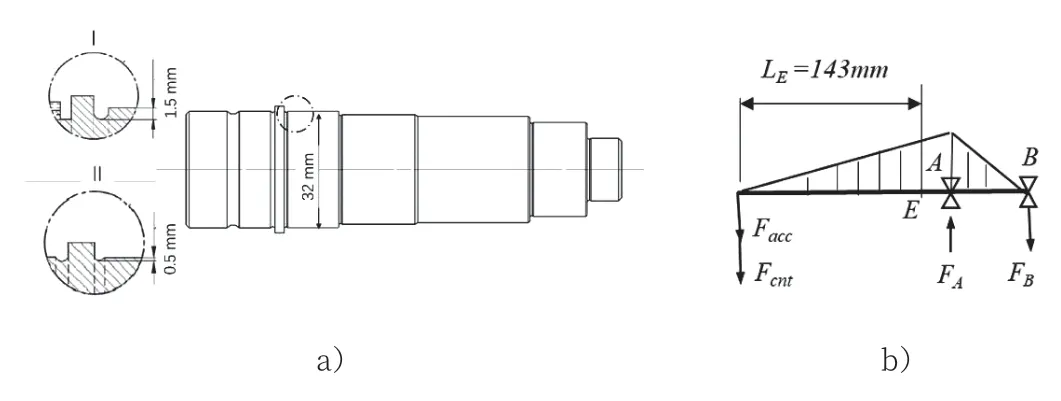
图3 主轴和弯矩

以上所有轴承寿命、主轴疲劳强度计算，均可编写Excel表格计算。针对不同制造商对滚筒结构强度验证测试要求，可方便的修改参数估算设计寿命系数。如要求洗衣机运行漂洗+脱水寿命试验3 750 周期，测试软件允许0.5 kg 偏心达成高速脱水，0.8 kg 偏心达成1 120 rpm 脱水，上述主轴的疲劳强度安全系数1.75，大轴承A 的寿命系数也大于1，满足强度试验要求。

图3 a）所示I 的环槽设计造成很大的应力集中，如果设计成II 所示的类似减荷槽结构，应力集中将降低，也不影响密封衬套的压装定位。

5 结论

前置式滚筒洗衣机驱动轴系统的轴承寿命、主轴疲劳强度，可通过模拟家庭负载的脱水偏心量频度分布和脱水转速控制曲线，得到一组类似载荷谱的变载荷离心力、离心力激发的受迫振动惯性力，应用疲劳损伤累积理论进行计算校核。以往的结构强度分析报告、公开文献都忽略了受迫振动惯性力对洗衣机结构强度的影响；上述给出的受力分析、疲劳强度计算表明，这个失误对驱动轴系统的寿命计算有非常大的影响；本文的计算方法和结论对洗衣机行业工程师在产品结构设计、试验结果的评判一定有很大帮助，同时对洗衣机外筒结构强度有限元分析精度的提高也有指导意义。