带有指令滤波的板球系统反步滑模控制的研究
2022-10-31孟圣钧韩光信白淏文路莹昕
孟圣钧,韩光信*,白淏文,路莹昕
(1.吉林化工学院 信息与控制工程学院,吉林 吉林 132022;2.中国电子科技集团 第十一研究所,北京 100020)
板球系统是欠驱动的高阶非线性系统,通过对其轨迹跟踪控制的研究为实际生产起到了理论指导的作用[1].目前,对于板球系统的跟踪控制问题,主要方法是依据板球系统运动学模型或动力学模型,通过滑模控制、自适应控制、神经网络控制、模糊控制等控制方法设计轨迹跟踪控制器[2-11],围绕着小球做定点、曲线运动而展开的系统鲁棒性研究.滑模控制作为一种常见的非线性控制策略,对模型的内部特性以及外部扰动不敏感,可应用于板球系统的轨迹跟踪控制中[2-5].文献[2]提出一种基于视觉伺服控制的轨迹跟踪方案,通过设计滑模控制器使系统具有较强的鲁棒性.但忽略了滑模控制导致的系统抖动现象,降低轨迹跟踪精度.文献[3]研究了反演自适应动态滑模控制方法,通过设计新的切换函数,有效解决了传统滑模的抖振问题,但轨迹跟踪误差较大.文献[4]设计出非线性自适应滑模控制器,提高了轨迹跟踪精度.但是,当球参数未知时,轨迹跟踪精度有待提高,难以适用这种方法.文献[5]采用结合系数的自适应解耦模糊滑模控制器设计方法,实现了板球系统的稳定控制,避免了复杂的计算,但其滑模表面的系数问题有待进一步更合理地解决,而且小球的速度越大,误差越大.以上方法均是针对滑模控制中遇到的抖振、参数变化影响轨迹跟踪控制等问题,提出相应的控制解决方案.文献[6-8]利用径向基函数神经网络算法,结合PID控制器在板球系统上完成方形轨迹跟踪控制和定位控制.其中,文献[6-7]采用LM算法替代梯度下降法整定PID控制参数,分实现RBF-PID控制的优化;文献[8]采用遗传算法优化PID参数,加强了系统控制的实时性.文献[9]提出一种自适应神经网络H∞控制方法,避免了backstepping方法的计算复杂性.文献[6-9]控制方案在一定程度上降低轨迹的震荡幅度,但跟踪精度有待提高.文献[10]设计了一种基于变论域模糊控制算法,改善了控制系统的动态品质.文献[11]引入蚁群算法,研究了基于蚁群优化的直接自适应模糊滑模控制方案,相比于文献[3-10]提高了轨迹跟踪精度.
板球系统通过电机控制驱动轴,进而控制平板上的小球运动,实现小球的定点运动、轨迹跟踪运动以及绕障运动,其快速高精准轨迹跟踪控制已成为当前研究的重难点.板球系统的轨迹跟踪控制目标是:在预定的控制动态品质下,让小球在复杂多变的运动场景中,能够按照参考轨迹完成高精准跟踪控制.本文针对板球系统受到的未知扰动影响轨迹跟踪性能这一问题,选取合适的滑模控制规律保证系统的快速跟踪性能和稳定性能,对滑模控制中出现的抖振现象以及小球位置信息提取过程中受到的干扰问题,将带有指令滤波功能的反步控制算法与滑模控制算法相结合,设计带有指令滤波的反步滑模控制器,实现板球系统的高精准轨迹跟踪控制.仿真实验表明,该控制方案在抑制系统扰动和消除抖振现象的同时,能够使小球快速、精准地跟踪预定曲线,使小球的轨迹跟踪误差不断收敛于零.
1 板球系统建模和控制方案问题描述
1.1 板球系统建模描述
板球系统有两个对称的X,Y轴子系统,每个子系统有4个自由度,分别是小球的位移和速度、平板的转角和角速度,板球系统实验台如图1所示.
本文在不影响系统性能的建模过程中,小球的滑动摩擦力和滚动摩擦力记为零,假设小球在平板上只有滚动且不会脱离平板,且平板的转角缓慢转动(一般不超过±5°).在平衡点xe=0处,分别在X,Y轴方向上对板球系统解耦、线性化后,利用拉格朗日方程建立板球系统数学模型,通过计算、简化后可得板球系统X,Y轴方向的状态方程为[12]:
(1)
其中,x1,x2,x3,x4和x5,x6,x7,x8分别为板球系统X,Y轴子系统小球的位移和速度、平板的转角和角速度.g表示重力加速度,系数k=m/(m+Jb/R2),m表示小球质量,R表示小球半径,转动惯量Jb=2mR2/5,ux,uy分别表示板球系统X,Y轴的控制输入.wx,wy分别表示板球系统X,Y轴受到的未知扰动.y1,y2分别表示板球系统X,Y轴小球的位置输出.
1.2 基于指令滤波的反步滑模控制方案
由于小球在平板上的运动不受约束,当小球以较大的速度运动时,摄像头采集小球的位置信息存在滞后现象,且小球X、Y两轴耦合性强.其次,小球自身的滚动摩擦、与平板之间的滑动摩擦以及外界不确定扰动等因素,都会影响系统的稳定性.为实现高精准的轨迹跟踪控制,本文基于滑模控制原理,依据系统跟踪误差设计滑模面,求得控制规律.进而引入二阶指令滤波器,滤除系统存在的量测噪声干扰,将反步法和滑模控制方法的优势相结合,提出了反步滑模控制策略,克服了滑模控制器产生的抖振问题[2],有效地抑制了系统受到的干扰,以增强系统的可靠性.基于指令滤波的板球系统X轴反步滑模控制方案如图2所示.Y轴设计方案参考X轴.
2 控制器设计及闭环稳定性分析
2.1 滑模控制器设计
滑模控制的主要思想是基于“滑动模态”运动,利用控制的不连续性使得系统在一定的条件下沿着预定的轨迹运动,对于由板球系统的结构不确定性、参数不确定性以及外界未知干扰等因素引起的扰动具有良好的鲁棒性,进而满足板球系统的轨迹跟踪控制性能要求.本文设计的滑模控制规律包括等效控制律和切换控制律两部分.因板球系统X,Y轴对称分布,Y轴方向的子系统控制器设计参考X轴.
根据式(1) X轴子系统选取误差方程:
(2)
其中,y0x为板球系统X轴方向输入信号.定义滑模切换函数:
s=b1e1+b2e2+b3e3+e4,
(3)
其中,常数bi>0(i=1,2,3).结合式(2),对式(3)求导后可得:
(4)

(5)
当板球系统受到未知扰动wx时,滑模控制律在等效控制的基础上还要考虑切换控制uwx来调节滑模运动的动态品质,提高系统克服未知扰动的能力.本文选择指数趋近律作为切换控制的主要组成部分[13]:
(6)
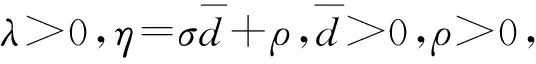
uwx=ηsgn(s)+λs,
(7)
结合式(5)和(7)可得总滑模控制规律为:
u1x=ueq+uwx.
(8)
2.2 带指令滤波的误差反步控制器设计
为了缓解外界未知扰动对小球反馈状态变量位置、速度的影响,本文针对误差反步控制律的状态量引入二阶指令滤波器,通过对小球位置和速度进行滤波处理,提高系统轨迹跟踪精度,抑制滑模控制器的抖振现象,进一步增强系统的稳定性.以板球系统X轴方向为例设计带指令滤波的误差反步控制器,Y轴方向设计参考X轴.引入二阶指令滤波器如下[14-15]:
(9)
其中,ξ为阻尼比,ωn为无阻尼自然频率.
结合式(1)中X轴方向子系统和式(9),构建带有二阶指令滤波的复合系统为:
(10)
结合式(10),定义系统偏差:
(11)
其中,e01=e1为小球位置误差;e02、e03、e04分别表示广义上的小球速度误差、平板转角误差和角速度误差;α1、α2、α3为虚拟函数,在后面进行定义.
结合式(10),对式(11)中e01进行求导:
(12)
(13)
定义虚拟函数α1:
α1=-c1e01(c1>0的常数),
(14)
代入式(13)得:
(15)
(16)
通过式(16)定义虚拟函数α2:
(17)
代入式(16)得:
(18)
(19)
通过式(19)定义虚拟函数α3:
(20)
代入式(19)得:
(21)
(22)
选取控制规律u0x:
(23)
结合式(10)、(11)、(12)、(14)、(17)、(20),化简式(23),可得带指令滤波的误差反步控制器为:
(24)
其中,f1=c1+c2+c3+c4,f2=c1c2+c1c3+c1c4,f3=c2c3+c2c4+c3c4,
结合式(8)和式(24)可得反步滑模控制规律为ux=u0x+u1x.
(25)
2.3 稳定性分析
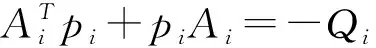
板球系统式(1)稳定性与输入和扰动无关[17],在X轴方向子系统中可令ux=0,wx=0,选取Lyapunov方程V5(x)=xTp1x(p1为实对称矩阵),求导得:
(26)
则式(1)中的X轴子系统是渐进稳定的.

(27)
此时,滑模控制系统能够达到稳定状态.
结合式(15)、(18)、(19)、(22)、(26)和式(27),可知:
(28)
那么,板球系统X轴方向闭环控制系统是渐进稳定的,同理可证Y轴方向闭环控制系统是渐进稳定的,则基于指令滤波的反步滑模控制系统是渐进稳定的.
3 仿真结果分析

(27)
图3~5分别为反步滑模控制的轨迹跟踪曲线、X,Y轴跟踪误差响应曲线和控制器输出曲线.作为对比,图6~8给出了增量PID滑模控制下的轨迹跟踪曲线、X,Y轴跟踪误差响应曲线和控制器输出曲线.
对比仿真实验结果可知,反步滑模控制X,Y轴跟踪误差绝对值的平均值分别为0.27 mm和0.233 mm;增量PID滑模控制X,Y轴跟踪误差绝对值的平均值分别为1.6 mm和2.13 mm.带指令滤波的反步滑模控制能够在预设的调节时间内2 s左右达到稳定状态,而增量PID滑模控制大约20 s左右达到稳定状态,全程带有抖振现象.当系统受到同样的外界未知干扰时,本文所提出的控制方案能够迅速克服扰动,保持较高的轨迹跟踪精度,鲁棒性强.
4 结 论
本文针对系统的轨迹跟踪控制问题,研究了带有二阶指令滤波器的反步滑模控制方案.在滑模控制过程中,结合等效控制律和切换控制律设计控制器,使得系统能够按照“滑动模态”进行轨迹跟踪运动.同时,采用反步法抑制系统的抖动,确保系统Lyapunov稳定.仿真结果验证,该控制算法有效地克服了滑模控制的抖振问题,使小球在预设时间内快速达到稳定跟踪状态,提高了系统控制性能.
