基于改进PSO 优化双尺度CNN 的齿轮箱故障诊断
2022-10-31孔子宇王海瑞
孔子宇,王海瑞
(650500 云南省 昆明市 昆明理工大学 信息工程与自动化学院)
0 引言
齿轮箱作为旋转机械中的关键传动部件,被广泛应用于各种大型机械,最常见的用途是机动车变速箱。在大型工程机械中,齿轮箱通常工作在较大的交变载荷条件下,且工作环境恶劣,导致齿轮箱出现磨损、齿轮断裂等故障,造成人员伤亡与财产损失[1],因此对齿轮箱故障的检测与诊断在机械装备的安全正常工作方面具有重要意义[2]。
齿轮箱的故障诊断方法大多是通过采集振动信号进行分析与诊断,该方法主要有故障特征提取和故障识别分类2 个步骤。传统的故障诊断方法是首先使用小波变换(Wavelet Transform,WT)[3]、快速傅里叶变换(Fast Fourier Transformation,FFT)[4]和经验模态分解(Empirical Mode Decomposition,EMD)[5]等信号处理方法进行故障特征的提取,再使用支持向量机(Support Vector Machine,SVM)、决策树(Decision Tree,DT)和多层感知器(Multilayer Perceptron,MLP)等方法进行故障分类。李众[6]等使用蜻蜓算法优化支持向量机,该模型有效提高了滚动轴承故障诊断的准确率,且收敛速度快、寻优能力强。WANG[7]等使用极限学习机燃油系统进行故障分类,并使用蝙蝠算法优化模型参数,弥补了极限学习机在分类精度和泛化能力上的不足。
近几年,随着深度学习(deep learning)技术[8]的不断进步,使用深度学习进行故障诊断的方法逐渐兴起。相较于传统的故障诊断方法,不需要丰富的故障特征提取经验。该方法不仅可以自动提取特征信息,还能学习到更加深层次的特征信息,避免了人工进行特征提取的操作,简化了使用流程。高统林[9]等将轴承振动信号转换为已知故障模式的振动信号振谱图,并使用卷积神将网络获得了很高的诊断准确率;胡茑庆[10]等将齿轮箱的故障振动信号进行经验模态分解得到内禀模式函数,该方法可自动化进行行星齿轮箱故障诊断;HE[11]等在残差网络的基础上进行了改进,添加了软阈值化方法,提高了噪声干扰下数据的诊断效果。
本文提出一种基于改进粒子群算法优化双尺度卷积神经网络的齿轮箱故障诊断方法,该方法通过使用双尺度卷积层,增加感受野,提高模型的特征提取能力,并改进粒子群算法的寻优方法,对诊断模型的结构参数及学习率进行优化,缩短模型的训练时间,提高故障分类准确率。
1 双尺度卷积神经网络
1.1 卷积层
卷积神经网络[12]的核心结构为卷积层,由数个卷积核及偏置矩阵构成。卷积核在输入数据上按一定距离滑动,每滑动到一个位置就会进行一次元素对应乘积并求和的运算,得到特征图(feature map)上的一个元素,具体计算公式为
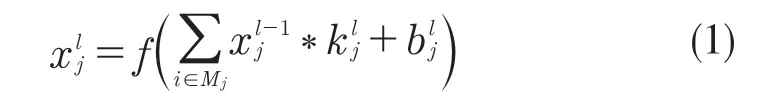
式中:xjl——第l 层中j个卷积核的输出值;——第l 层的第j个卷积核;bjl——第l 层的第j个卷积核的偏置项;*——卷积操作;f——激活函数。
本文选取的激活函数为ReLU 函数[13]:
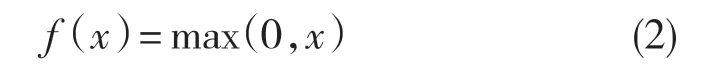
该函数的特点是解决了部分梯度弥散问题,并加快了网络训练速度。在每层卷积层后使用批标准化(batchnorm)[14],使输出平滑化,减少损失函数的变化量并限制其梯度,数学表达式为
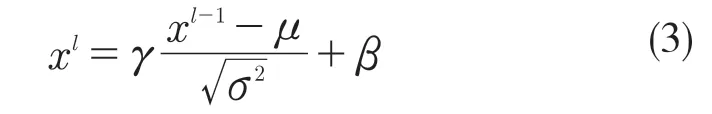
式中:xl——第l 层的输出值;μ——输入值的平均值;σ——输入值的方差;γ,β——可训练的参数来调整和缩放输出值。
1.2 池化层
加入池化层的目的是减小特征图的大小。由于卷积层会使通道数增加,加入池化层不仅可以减少计算量和资源消耗,还能增大感受野。常用的池化方法有最大池化与平均池化,这些方法计算简单又能突出数据的主要代表特征。本文选取最大池化方法作为池化层,其数学表达式为

式中:l——网络层数;——上一层输入的第i个通道的第n个值。
1.3 全局平均池化层
全局平均池化是对各通道的特征图分别计算平均值。传统的卷积神经网络的分类模块大多是叠加数个全连接层,这样就会使网络的参数过多,不利于模型的训练。使用全局平均池化不需要参数,避免了使用全连接层出现的过拟合现象,还不损失各特征图之间的空间位置信息,其数学表达式为

式中:xil——第l层的输出值中第i个通道的特征图。
1.4 模型整体结构
本文所用卷积神经网络模型如图1 所示。该模型使用“端到端”的方式进行训练,即在输入层不使用特征提取方法对输入数据进行处理,仅使用标准化等必要方法对数据进行规整。多尺度卷积结构可以提取到不同尺度的特征,并能降低模型的复杂程度与计算量。在本模型中加入了双尺度卷积结构,由多个不同尺度的卷积层或池化层构成,最后对输出数据进行通道融合。
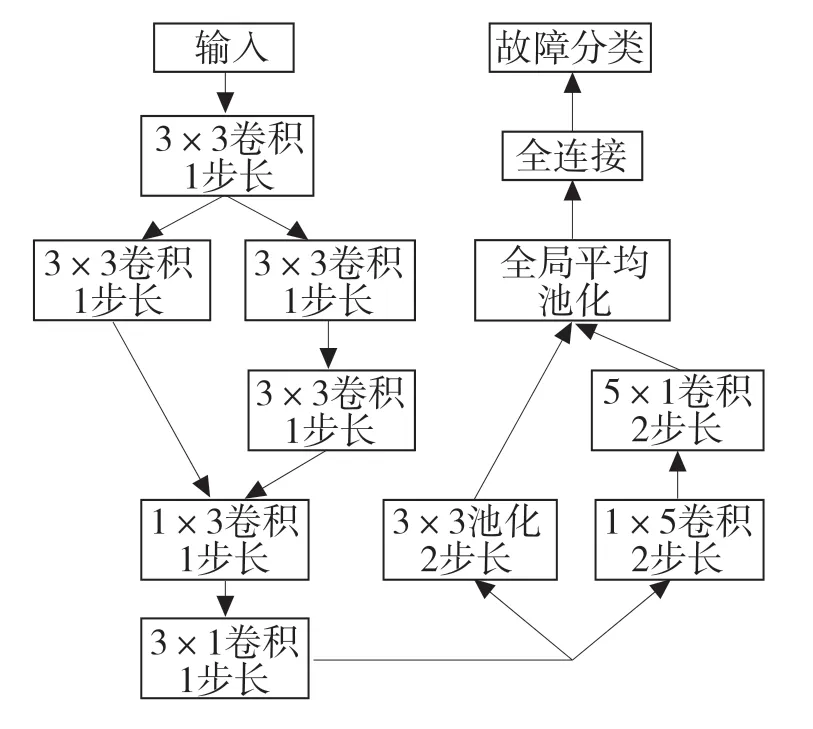
图1 双尺度卷积神经网络模型结构图Fig.1 Dual-scale convolutional neural network model structure diagram
在第1 个双尺度卷积结构中连续使用2 个3×3 卷积层来代替5×5 卷积,在降低了28%计算量的前提下使输出特征与5×5 卷积相同。本模型还在第2 个双尺度卷积结构中使用了非对称卷积结构,通过将n×n大小的卷积操作分解为1×n卷积和n×1 卷积,在精度略微下降的前提下可将该层的计算量降低33%。在模型最后的分类部分使用全局平均池化(Global Average Pooling,GAP)与全连接层进行故障分类,其中全连接层使用softmax函数作为激活函数。
1.5 训练方法
本模型使用负对数似然函数作为损失函数,该函数通过评价样本出现的概率来最小化损失,其数学表达式为
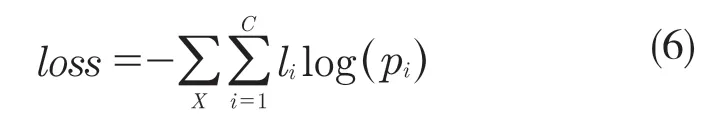
式中:X——one-hot 形式的观测值;C——类别;l——真实值;p——测值。
优化算法使用Adam 优化算法[15]对本模型的权重进行优化,通过加入动量因子和使用自适应学习率来加快收敛速度。相较于传统的梯度下降优化算法,该算法计算效率更高,对内存的需求更小,对嘈杂或稀疏的数据适应度较好。
2 改进的粒子群超参数优化方法
2.1 粒子群算法基本原理
粒 子 群 算 法(Particle Swarm Optimization,PSO)是一种基于全局优化的演化计算技术,属于一种万能启发式算法,能在没有太多问题信息的情况下,有效搜索具有庞大解空间的问题并找到候选解。
该算法的基本原理:在一个维度为n的搜索空间中,定义一个由m个粒子组成的集合X={x1,x2,x3,x4,…,xm},第i个粒子的速度记做vi=(vi1,vi2,vi3,vi4,…,vin)T,其最佳位置记录记做pi=(pi1,pi2,pi3,pi4,…,pin)T,全局位置记录记做pg=(pg1,pg2,pg3,pg4,…,pgn)T,该算法通过不断迭代更新每个粒子的位置,每次迭代的数学表达示为
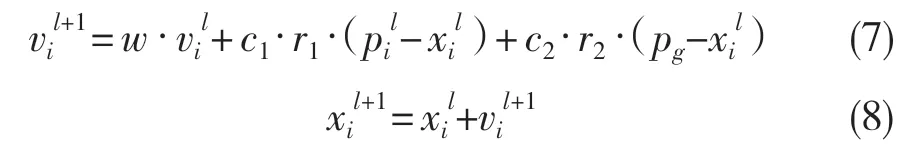
式中:l——迭代次数;w——惯性权重;c1、c2——加速常数;r1、r2——0~1 的随机因子。
粒子群算法的主要特点是简单易实现、参数少和收敛快,但是其精度较低易发散,若参数设置不当可能会错过最优解甚至使算法不收敛。
2.2 算法的改进
为增强粒子群算法的寻优能力,本文提出一种对该算法进行改进的方法,可在计算量大致相同的情况下进一步优化其精度。改进方法:在每个粒子周围选取z个距离为d的不同随机点s,第i个粒子的随机点可记做si=(si1,si2,si3,si4,…,siz)T,每个随机点方向的适应度记做psi=(psi1,psi2,psi3,psi4,…,psiz)T,通过比较随机点的适应度进行迭代,并更新每个粒子的位置,每次迭代的数学表达式为
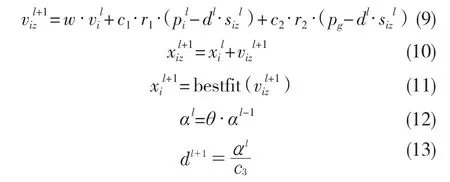
式中:l——迭代次数;w——惯性权重;c1,c2——加速常数;c3——步长常数;r1,r2——0~1的随机因子;α——变步长因子;θ——变步长因子的衰减值;bestfit()——选取最优适应度。
2.3 适应度计算方法
传统的适应度计算方法是直接使用神经网络预测准确率作为其适应度,为保证神经网络在训练时收敛更快,本文方法按固定迭代间隔选取N 个神经网络训练时的输出准确度,则所有被选用准确度可表示为P=(P1,P2,P3,…,PN)T。具体计算方法是使用均方误差函数(Mean Square Error,MSE)求选取准确度与100%之间的误差值,该函数的特点是易于计算,由于经过了平方,目标值偏差较多时会受到更高的惩罚。该方法的数学表达式为

2.4 超参数优化步骤
具体优化卷积神经网络的流程如图2 所示。第1 步,提取齿轮的故障信号,由于本文使用“端到端”的方法,仅对数据进行归一化处理,再将数据集划分为训练集、测试集和验证集;第2 步,使用改进的粒子群算法优化卷积神经网络的结构参数与学习率,使用测试集计算适应度;最后,使用验证集测试调优后的卷积神经网络并输出故障类型。
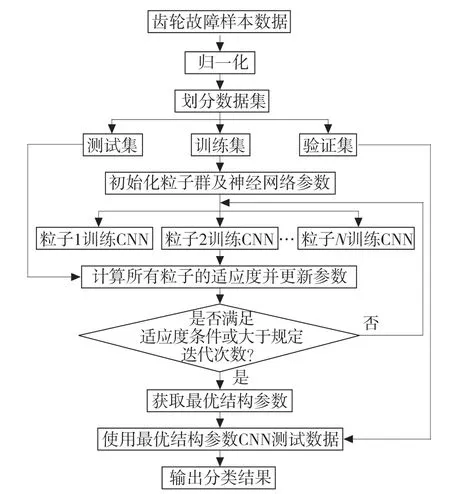
图2 改进PSO 优化CNN 流程图Fig.2 Improved PSO optimized CNN flowchart
3 实验与分析
3.1 实验数据
本文使用东南大学齿轮箱数据集[16]对方法进行实验与分析。该数据集由传动系统动态模拟器(Drivetrain Dynamic Simulator,DDS)进行数据采集,实验装置如图3 所示。数据集包含了20 Hz-0 V 和30 Hz-2 V 两种工况下的数据。每种工况包含齿面磨损、轮齿折断、齿根断裂和齿面点蚀4 种故障;每种故障包含以下8 种信号:电机振动,电机扭矩,行星齿轮箱的x,y,z三个坐标轴方向的振动信号,并联齿轮箱的x,y,z三个坐标轴方向的振动信号。

图3 齿轮数据采集实验台Fig.3 Gear data acquisition test bench
本文选取30 Hz-2 V 工况下并联齿轮箱的3 个坐标轴方向的振动信号作为实验用数据构建数据集,每条数据样本对每个方向的采样长度为1 024,并转换为三通道大小为32×32 的二维图像,每个通道分别为不同方位传感器所采集的数据,每种工作状态各构造1 024 个样本,通过乱序分层抽样的方法划分训练集、测试集和验证集。各故障样本数据由表1 所示。
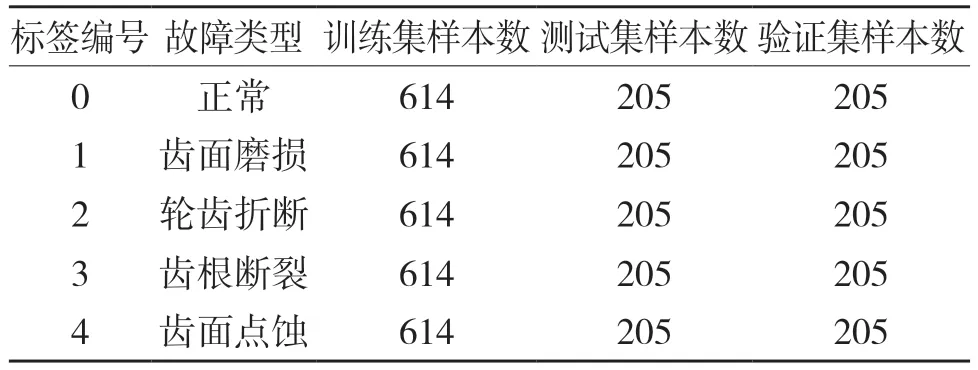
表1 齿轮数据集样本信息Tab.1 Sample information of gear data
为验证本方法的有效性,选用粒子群算法、遗传算法(Genetic Algorithm,GA)和萤火虫算法(Firefly Algorithm,FA)进行超参数优化算法的性能对比分析,选用常用的故障诊断方法BPNN,PSO-SVM,LSTM 和DBN 进行模型分类准确度对比分析。由于以上所选的故障诊断方法的部分参数为随机初始化,为避免因随机参数导致的性能波动,在每次进行实验之前,使用固定随机种子的方法让每次实验中模型参数的初始化值相同。实验环境为Ubuntu 21.04 LTS 操作系统,CPU 为Intel XEON E5-2680 v2,GPU 为NVIDIA GeForce RTX 2060,编程语言使用Python。
3.2.1 超参数优化算法性能对比分析
本次实验所选用的各优化算法的初始化参数为:PSO 中的惯性权重w取0.6,学习因子c1,c2均取2;GA 中的变异概率取0.01,交叉概率取0.5;FA 中的光强吸收系数,初始吸引度均取1。本文方法的参数随机点数量z取1,步长常数取5,变步长因子衰减值取0.95,种群规模取50 其他均与PSO 参数相同。其余算法的种群规模和最大迭代次数均取100。实验得到的性能对比图如图4 所示。
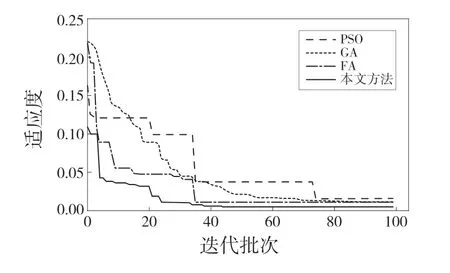
图4 不同优化算法的性能对比Fig.4 Performance comparison of different optimization algorithms
由图4 可以得到,使用4 种优化算法优化都能在100 次迭代内得到较好的结果。其中,PSO 的收敛性较差,在第73 轮之后才达到其最佳适应度,且更新频率慢、搜索效率低。相比于PSO,GA 与FA 的搜索效率较高,但不如本文方法。本文方法改进了PSO 的寻优方式,在种群规模为50 的情况下仍能达到最优的适应度,且极大地改善了PSO搜索效率较低的问题,在第40 轮左右即可找到最优适应度。因此,本文的超参数优化方法相对于其他常用的超参数优化算法具有明显优势。
通过上述实验信息可确定神经网路的最优参数:初始卷积层的输出通道数取24,第2 个双尺度卷积结构的输出通道数取46,学习率取0.000 135。
3.2.2 模型分类准确度对比分析
本实验使用的各故障诊断方法的参数与输入数据处理方式为:BPNN 的结构选用3096-1536-768-384-96-5,将输入数据的3 个维度拼接成一维,不进行特征提取;SVM 中的核函数使用高斯核函数,其余参数使用PSO 优化,使用VMD 与样本熵进行特征提取;DBN 的结构与BPNN 相同,但最后一层使用BPNN 进行分类,由高斯-伯努利受限玻尔兹曼机堆叠构成,每层的学习率取0.003,动量值取0.98,数据处理方式与BPNN 相同;LSTM模型由3 层LSTM 层加2 层全连接层构成,将输入数据结构转换为二维时间序列数据。以上的神经网络结构使用交叉熵损失函数和Adam 优化方法,批大小均取32。对比结果如表2 所示。

表2 各方法测试集与验证集准确率Tab.2 Accuracy of test set and verification set of each method
由表2 可以看出,本文方法的诊断识别率更加优秀,验证集与测试集的结果的差值也较小。LSTM 的结果次之。PSO-SVM 的验证集准确率与测试集准确率差距较大,因为SVM 是浅层学习方法,无法像深度学习学习到深层次的特征,并且依赖与人工故障特征提取,故导致准确率波动较大。BPNN 与DBN 使用一维数据进行诊断,无法很好地得到数据的空间信息,导致准确率较低。
本文方法与其他两种深度学习方法的训练稳定性结果如图5所示。其中,BPNN的前期波动较大,在15 轮之后趋于平稳;LSTM 则在前期的收缩较慢,25 轮之后趋于平稳。本文方法在第5 轮时即能达到其最高的准确率,表明其稳定性与收缩速度比其他两种方法更加优秀。
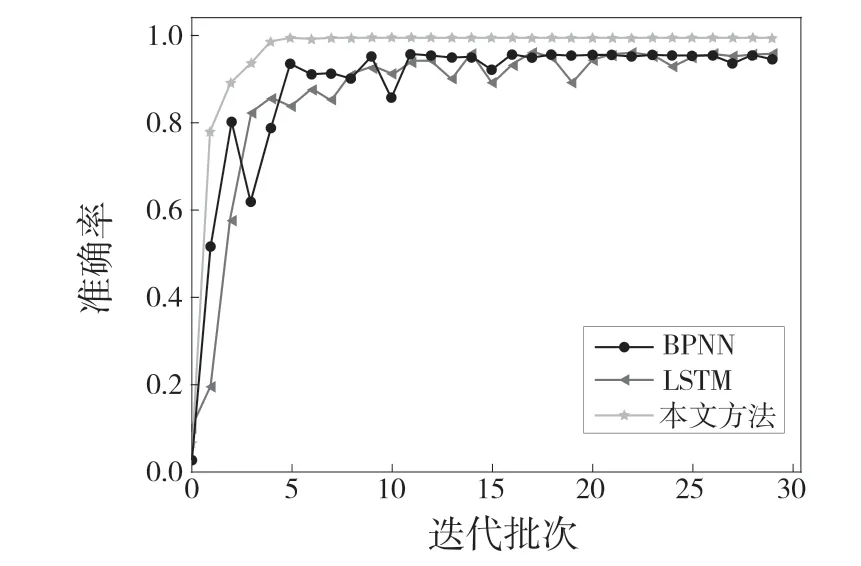
图5 深度学习方法模型稳定性对比Fig.5 Stability comparison of deep learning models
为了显示本文方法的特征提取能力,通过使用t-分布随机邻域嵌入(t-distributed Stochastic Neighbor Embedding,t-SNE)将GAP 层的输出数据降维至三维,数据可视化后的结果如图6 所示。从图6 可以看出,各类别的数据已被明显地区分开来,表明本文方法中的多尺度卷积层可以有效提取故障特征,有较好的分类性能。
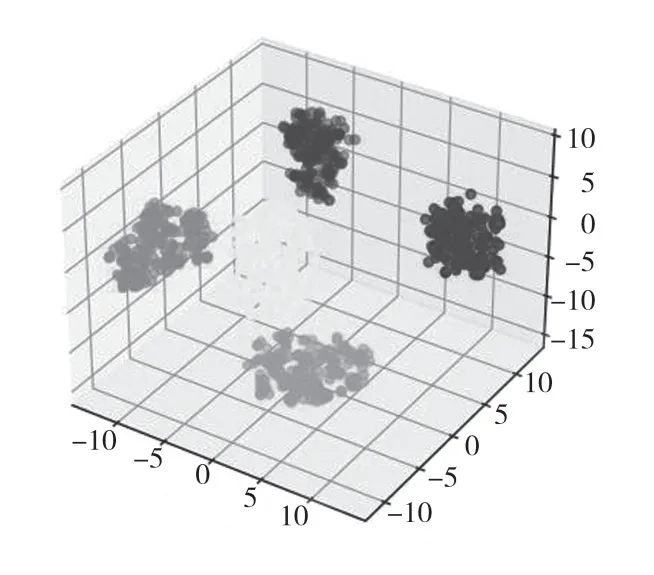
图6 故障特征可视化Fig.6 Fault feature visualization
4 结语
本文提出了一种基于改进粒子群优化双尺度卷积神经网络的齿轮箱故障诊断方法。与常见的启发式优化算法和故障诊断方法对比得出如下结论:
(1)本文模型使用“端到端”的方法最大限度减小了因人工故障特征提取导致的特征损失,并使用双尺度卷积层加快训练速度,减少训练参数,对比常见的故障诊断方法有一定的优势。
(2)使用改进的粒子群优化算法比常用的优化算法在收敛性和搜索时间方面有了明显改善。
