金属盖结构参数对其密封性能的影响

陶鑫，何邦贵，王成位，刘旺清

（1.650000 云南省 昆明市 昆明理工大学 机电工程学院；2.650000 云南省 昆明市 云南唯佳塑业有限公司）

0 引言

金属作为包装材料，其机械性能、保护性能与加工性能都非常优秀。并且，金属资源丰富，其作为包装材料的能耗与成本较为低廉，制作工艺较为成熟。同时，金属能重复回收利用，是理想的绿色材料。所以金属作为包装材料的运用日渐广泛，在包装加工产业中占有极其重要的地位[1]。金属材料具有良好的安全性、密闭性以及环保性，其作为包装行业的重要材料已持续十几年高速发展，随着国民消费习惯的升级，大量的包装物中都运用了安全与稳定的金属材料[2]。目前，我国的金属包装材料用量仅次于塑料，而美国包装产品中的金属用量比塑料还多，居第2 位[3]。金属作为具有稳定性能的包装材料拥有良好的塑性变形能力，且其防潮与阻断性能均优于其他常见包装材料，可有效保护其内装商品[4]，因此适合作为包装密封件对产品进行保护。对金属密封件的密封性能进行研究，可延长产品的稳定性周期、保持商品的功能特性，其分析结果具有良好的现实意义。

目前，对包装金属密封件与塑料容器配合的密封性能研究较少，但是对于金属包装容器与用于其他领域弹性金属密封件的性能研究却较为成熟。杨丹[5]等为研究金属包装容器的气体密封问题，建立了金属容器二重卷封结构的气体粘滞流泄漏模型，为金属容器设计与密封性能控制提供了一定的理论依据；曹利杰[6]等对金属包装容器的封合与密封方式进行了分析，分析了金属容器包装封口缺陷产生的原因，并提供了相应的解决方案。在其他技术领域，王刚[7]等采用 ANSYS Workbench 建立了O 型密封圈的轴对称分析模型，并对不同压缩率与不同载荷下的密封圈应力应变进行分析，得到了密封圈与压缩率与载荷之间的密封规律；迪力夏提·艾海提[8]等基于有限元软件分析了Y 型密封圈唇开口宽度、摩擦因素以及唇口长度对密封圈最大接触应力的影响情况，并找出了影响其可靠性的主要参数；王冰清[9]等利用ANSYS 分析软件，通过建立丁晴橡胶星型密封圈的二维轴对称模型对其工作状态下的密封机理与密封性能进行了分析，并成功预测了星型密封圈发生失效的具体部位。

综合上述研究成果与相关研究分析可知，使用有限元方法与有限元软件对密封件进行性能分析是一种成熟且有效的手段与方法，因此其也同样适用于包装金属密封盖的密封性能研究。在目前对密封件的研究基础上，使用有限元软件对其密封性能进行分析计算是最直观且有效的研究方法。

1 三维轴对称计算模型

图1 所示为金属密封盖与塑料瓶口过盈配合的结构示意图。图1 中：R——配合面槽口倒圆半径；a——金属盖配合面截面厚度；b——密封槽高度；θ——配合面倾角大小。

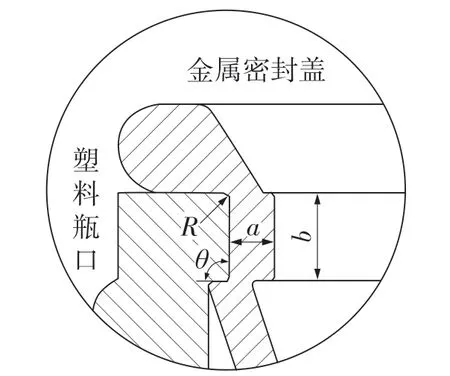
图1 过盈配合结构示意图Fig.1 Schematic diagram of interference fit structure

1.1 基本假设

根据金属盖与塑料瓶口的过盈配合与尺寸模型，可将其视为由2 个圆筒套合在一起，即服从薄壁圆筒过盈配合理论模型。根据弹性理论，此配合模型满足以下条件：（1）假定物体具有对称性；（2）假定物体是连续的，即假定整个物体的体积都被组成这个物体的介质所填满；（3）假定物体完全服从胡克定律，应变与引起该应变的那个应力分量成比例；（4）假定物体是均匀的；（5）假定物体是各向同性的，且位移与形变是微小的[10]。

1.2 有限元模型

密封金属盖材料为铝制合金，外径66 mm，内径64 mm，杨氏模量E=70 000 MPa，泊松比为0.34；瓶口材料为PET 塑料，外径71 mm，内径65.9 mm，杨氏模量E=2 500 MPa，泊松比为0.3；静态工作状态下配合过盈量δ=0.05 mm。基础结构参数尺寸：配合面槽口倒圆半径R=0.1 mm，金属盖配合面截面厚度a=1 mm，密封槽高度b=2 mm，配合面倾角θ=90°。

使用ANSYS Workbench 软件建立金属密封盖与塑料瓶口过盈配合结构且考虑接触的微小形变三维轴对称模型，并在此基础上计算工作状态下过盈配合的变形与应力。三维模型与有限元网格如图2所示。为排除网格划分对计算模型的影响程度，同时降低非必要部分计算的时间长度，将配合面网格精度调整至0.3 mm，将瓶身非配合部分网格精度设置为1.0 mm。依据圣维南原理，距离受力配合面的远处所受到的影响可忽略不计，可以将瓶身长度削减，同时将固定约束设置于瓶身最底部，使计算模型接近于实际配合模型。经过以上分析设置，划分有限元模型，最终得到节点数为551 634 个，单元数为203 316 个。

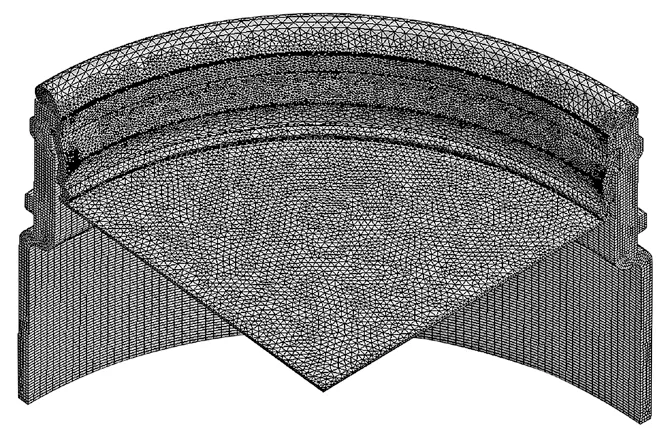
图2 过盈配合结构与网格划分Fig.2 Interference fit structure and meshing

2 理论计算与验证分析

2.1 薄壁过盈配合理论计算

如图1 所示，金属盖外壁凹槽与塑料瓶口内壁凸起进行过盈配合，可对工作状态下的接触面进行径向截面分析，接触面与密封组件位置近似于薄壁过盈配合理论模型，如图3 所示。图3 中，A表示金属盖内径，B为配合面半径，C表示塑料瓶口外径，P为过盈配合装配压力。

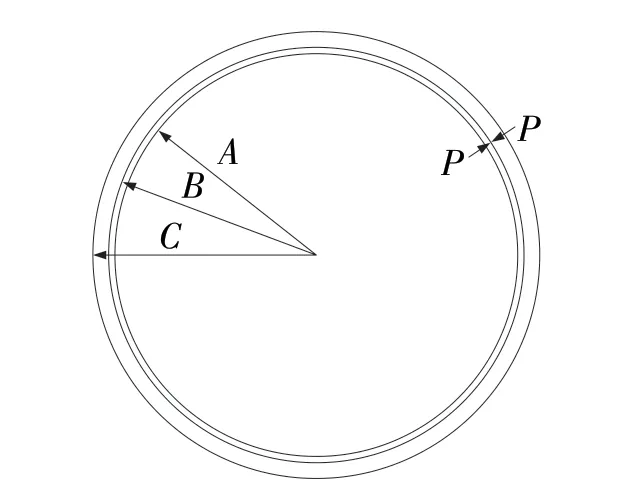
图3 过盈配合径向截面Fig.3 Interference fit radial cross section

由过盈配合理论可知，塑料瓶口内半径小于金属密封盖的外半径数值，两者之间的差值δ即为工作状态下的过盈量。当金属密封盖装入瓶口后，其接触面上产生相互压紧的装配压力P，对金属密封盖而言即为外压力P，对瓶口而言相当于内压力。

结合薄壁圆筒过盈配合理论与弹性力学中轴对称问题的基本方程，可通过公式对金属密封盖工作状态下的应力大小、半径缩短量以及装配压力进行计算[11]。

径向应力计算公式：

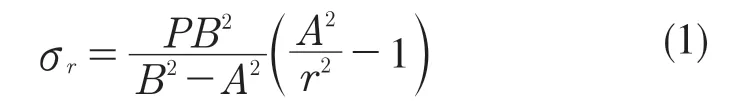
周向应力计算公式：

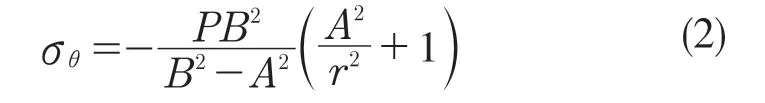
金属密封盖外径缩短量：

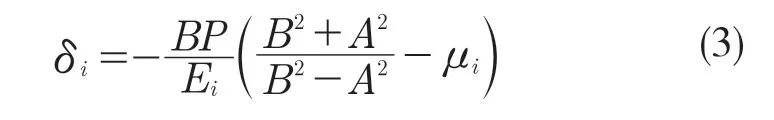
塑料瓶口内径伸长量：

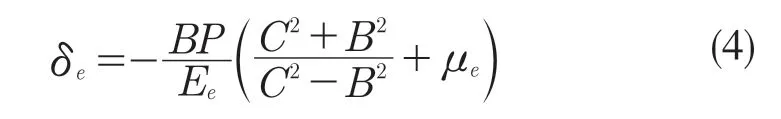
过盈配合装配压力：

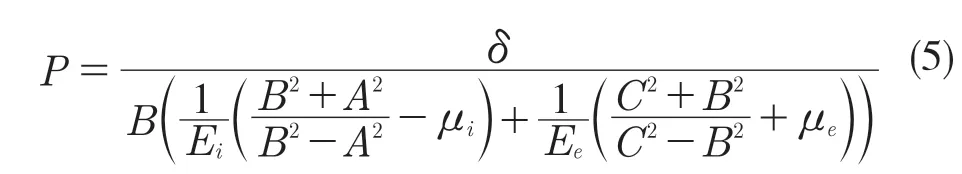
式（1）—式（5）中：r——计算过程中任意位置的半径值；Ei——金属密封盖弹性模量；μi——金属盖泊松比；Ee——塑料瓶口弹性模量；μe——塑料瓶口泊松比。

综合上述计算公式与金属密封盖配合的基础尺寸，可得到如下理论计算结果：

2.2 仿真分析验证

使用ANSYS Workbench 求解器模块对图2 所示的三维轴对称模型进行有限元分析，得到金属密封盖配合面与瓶口变形量、金属盖应力分布情况如图4 所示。

图4 仿真计算结果Fig.4 Simulation results

将图4 有限元仿真分析结果与式（6）的理论计算数值对比，结果如表1 所示。

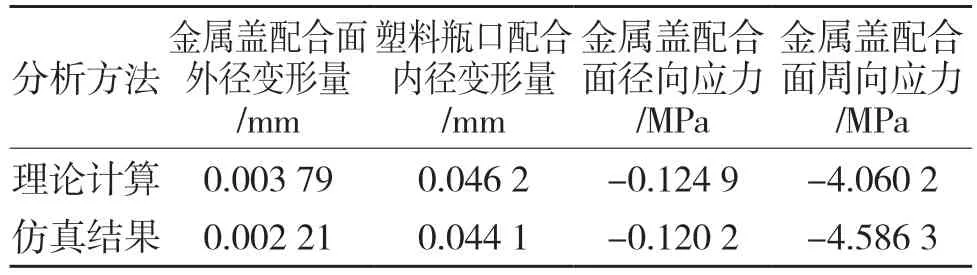
表1 理论与仿真结果对比Tab.1 Comparison of theoretical and simulation results

由表1 数据 可知，本文三维轴对称模型的有限元分析结果与理论数值之间误差较小，验证了模型分析的合理性、适用性，在此有限元模型基础上对包装密封性能进一步研究具有一定的准确性。

3 金属密封盖结构设计参数分析

图5 为金属密封盖在密封包装工作状态下的von-Mises 应力分布示意图。由图5 可见，金属密封盖受过盈配合面的挤压且最大应力分布在配合面的最下方。由于包装过盈密封的必要条件是密封配合面上的最大接触应力不小于包装物对瓶口的工作压力，而图5 中密封配合面的最下方为应力的最大产生部位，因此对金属密封盖结构参数的影响以讨论结构参数对接触面最下方的接触应力变化为主。

图5 金属密封盖von-Mises 应力分布图Fig.5 Von -Mises stress distribution of metal seals

影响金属密封盖结构参数的主要因素是配合面槽口倒圆半径、配合面截面厚度、密封槽高度、配合面倾角以及金属盖表面摩擦系数。不同结构参数对包装密封性能产生不同影响，分析参数的影响能为包装密封结构设计奠定一定基础。

3.1 配合面槽口倒圆半径对接触应力的影响

以三维轴对称模型为对象，研究配合面槽口倒圆半径与密封性能间的关系，采用控制变量法对单一变量进行控制。包装金属密封盖过盈配合属于微变形量，将倒圆半径R限制在0.10～0.30 mm，间隔0.05 mm，所得接触应力变化模型结果如图6 所示，仿真数据变化趋势如图7 所示。

图6 不同倒圆半径下接触应力的分布情况Fig.6 Distribution of contact stress under different radius of inverted circle

从图7 所示，接触应力随着配合面槽口倒圆半径的变化而发生波动，在倒圆半径为0.15 mm 时发生上升趋势，在0.25 mm 时发生回落，并在半径为0.3 mm 时再次上升。当倒圆半径从0.1 mm 增加到0.15 mm 时，接触应力数值发生迅速上升，但在后续变化中接触应力增量较小，因此倒圆半径选择0.15 mm 即可。

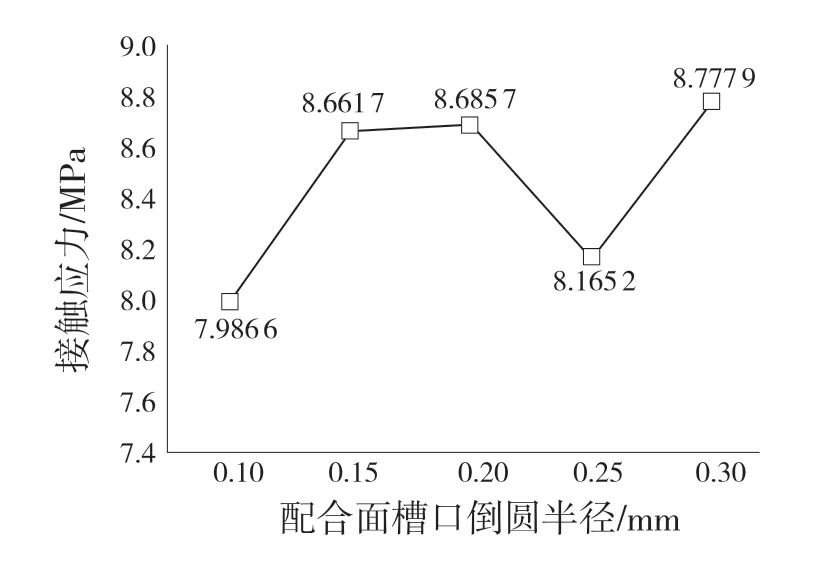
图7 不同倒圆半径下接触应力的变化趋势Fig.7 Variation trend of contact stress under different radius of inverted circle

3.2 配合面截面厚度对接触应力的影响

保持金属盖其他基础结构参数不变，以配合面截面厚度a为单一变量，对其变化下的接触应力进行仿真计算。将截面厚度范围控制在1.0～1.5 mm之内，间隔为0.1 mm，所得接触应力变化模型结果如图8 所示，仿真数据变化趋势如图9 所示。

图8 不同截面厚度下接触应力的分布情况Fig.8 Distribution of contact stress under different section thickness

如图9 所示，配合面截面厚度为1.1 mm 时，接触应力达到极值；当截面厚度1.1 mm 后，接触应力随着配合面截面的变化而发生上下波动。因此选择截面厚度为1.1 mm 的金属密封盖，可获得在厚度变化范围内较大的接触应力值，能使包装容器的过盈密封配合更为紧固。

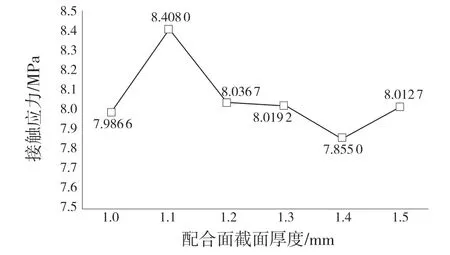
图9 不同截面厚度下接触应力的变化趋势Fig.9 Variation trend of contact stress under different section thickness

3.3 密封槽高度对接触应力的影响

对金属密封盖密封槽高度数值的影响进行仿真模拟，将密封槽高度范围控制在2～4 mm 之间，间隔为0.5 mm，所得接触应力变化模型结果如图10 所示,仿真数据变化趋势如图11 所示。

图10 不同密封槽高度下接触应力的分布情况Fig.10 Distribution of contact stress under different sealing groove heights

由接触应力变化趋势图所示，当配合面密封槽高度大于2 mm 后，接触应力分布趋于平滑且应力分布更为均匀。由图11 可知，当密封槽高度为2 mm 时，接触应力数值明显大于2.5～4.0 mm 区间内的应力大小，因此为保证良好的包装密封性能，配合面密封槽应选择2 mm 高度。

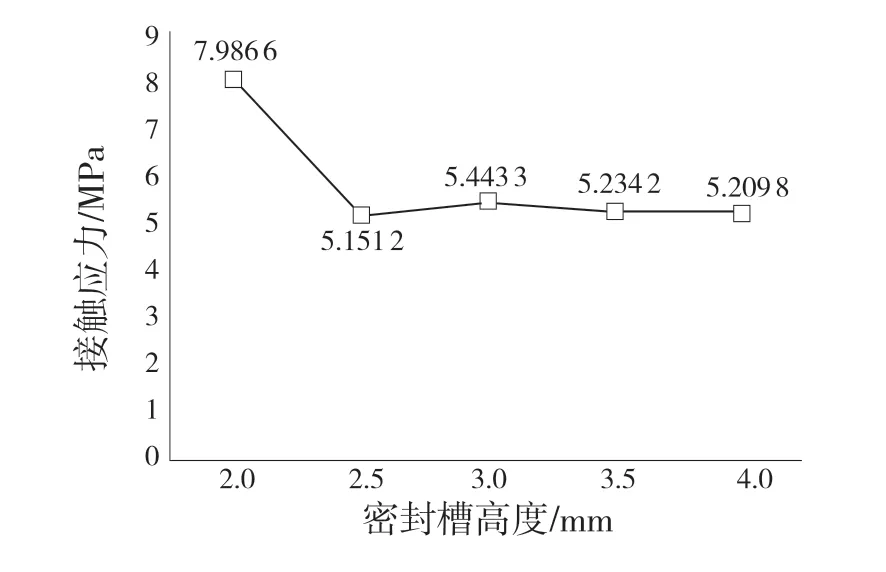
图11 不同密封槽高度下接触应力的变化趋势Fig.11 Variation trend of contact stress under different sealing groove heights

3.4 配合面倾角对接触应力的影响

如图1 所示，不同配合面倾角θ对包装过盈密封接触应力会产生影响。对不同倾角下的过盈密封情况进行模拟分析，将配合面倾角范围限制在80°～100°之间，倾角间隔为5°，所得接触应力变化模型结果如图12 所示,仿真数据变化趋势如图13 所示。

图12 不同倾角下接触应力的分布情况Fig.12 Distribution of contact stress at different dip angles

如图13 所示，当倾角小于90°时，接触应力大小先增后减；当倾角大于90°时，接触应力随角度的增大而增大。比较倾角85°与100°时的接触应力数值，85°时数值略小，但倾角达到100°时，瓶口部分容易产生环形凸起，不利于金属密封盖的压紧配合。因此综合考虑应选择倾角为85°的结构方式。

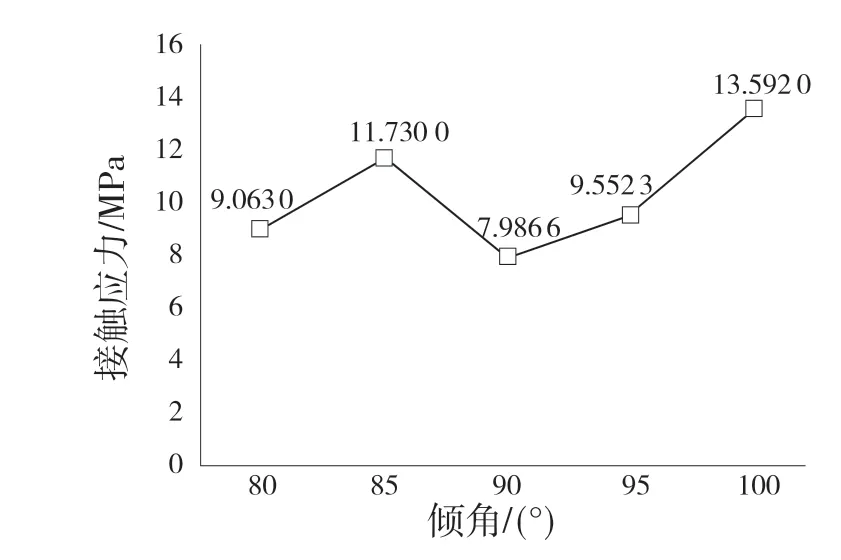
图13 不同倾角下接触应力的变化趋势Fig.13 Variation trend of contact stress at different dip angles

3.5 表面摩擦系数对接触应力的影响

表面摩擦系数是影响密封联接轴向力传递的重要因素，若表面摩擦系数增大，则所配合的密封组件所受的轴向力会偏小，且密封状态配合面下容易产生滑动；若表面系数数值偏小，则装配时的配合难度会增加，使得包装密封的非接触面上产生应力集中[12]。对表面摩擦系数变化下的接触应力变化情况进行仿真计算。将摩擦系数控制在0.05～0.25之内，间隔为0.05，所得接触应力变化模型结果如图14 所示，仿真数据变化趋势如图15 所示。

图14 不同摩擦系数下接触应力的分布情况Fig.14 Distribution of contact stress under different friction coefficients

如图15 所示，接触应力随摩擦系数的增大先降后升，摩擦系数为0.15 时达到极小值，摩擦系数大于0.15 后，接触应力逐渐增加。

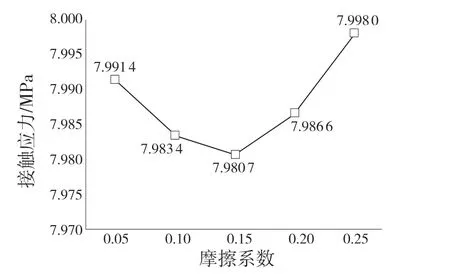
图15 不同摩擦系数下接触应力的变化趋势Fig.15 Variation trend of contact stress under different friction coefficients

但从数值大小上考虑，摩擦系数对接触应力大小影响不明显，波动范围较小，对此结构的密封性能影响不大，因此选择摩擦系数0.25 即可满足此包装的密封需求。

4 结语

为研究金属盖结构参数对其密封包装性能的影响，本文建立了包装容器结构的有限元计算模型，并对此密封结构进行了不同参数下的有限元分析。结果表明，金属密封盖受过盈配合面的挤压且最大应力分布在配合面的最下方。配合面倾角为此容器结构密封性能的主要影响因素，当密封槽高度大于2 mm 后，接触应力会出现断崖式下跌，然后趋于稳定，而接触应力随配合面槽口倒圆半径、配合面截面厚度与表面摩擦系数的变化发生波动，对密封性能的影响较小。因此，对于与此结构相似的包装密封联接，在金属盖的结构参数研究应重点分析倾角与密封槽高度对其接触应力的影响。对比本文的有限元分析计算，为满足包装的良好密封性能，金属盖结构参数应选择配合面槽口倒圆半径为0.15 mm、配合面截面厚度为1.1 mm、密封槽高度2 mm、配合面倾角85°以及0.25 的表面摩擦系数。