多约束条件下某智能飞行器质心平衡优化

赵朝辉，王志昊

（200093 上海市 上海理工大学 机械工程学院）

0 引言

随着现代技术的发展，智能无人机在航空植保、测绘勘查、快递运输等领域得到广泛应用[1]。智能飞行器的姿态控制是控制系统的核心，而飞行器的质心变化对飞行器的控制有着重要的影响[2]。飞行过程中，各油箱的含油量和俯仰角会随飞行器的运行不断发生改变，从而导致飞行器的质心位置随之变化[3]，故需要建立数学模型来优化供油策略，以达到飞行器的质心动态平衡的目的。而多约束条件下对无人机多个油箱供油策略计算时采用全局遍历算法会造成计算成本极大，因此本文采用贪心算法和粒子群算法扩展而来的LDMPSO，计算智能飞行器飞行过程中理想质心的轨迹以及合理的供油策略。

1 油箱分布和飞行约束

1.1 油箱分布

假设该飞行器一共有6 个油箱，各油箱供油示意图如图1 所示。

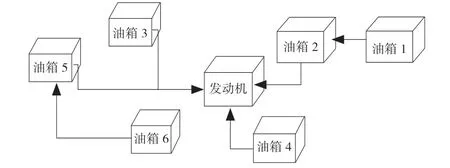
图1 飞行器油箱供油示意图Fig.1 Schematic diagram of aircraft fuel tank fuel supply

1.2 飞行约束

（1）油箱均为长方体且位置固定，其内部长、宽、高方向分别平行于飞行器坐标系的x、y、z轴方向；

（2）在飞行器坐标系下，飞行器（不载油）质心为（0，0，0），第i个空油箱中心位置为，i=1，2，…，6 ；

（3）第i个油箱的供油速度上限为Ui（Ui＞0），i=1，2，…，6。每个油箱一次供油持续时间不少于60 s；

（4）主油箱2—5可直接向发动机供油，油箱1、6 作为备份油箱分别为油箱2、5 供油（如图1）；

（5）受到飞行器结构限制，至多2 个油箱可同时向发动机供油，至多3 个油箱可同时供油；

（6）飞行器各油箱联合供油总量应满足发动机对耗油量的需要，多余燃油排出飞行器；

（7）为简化问题，仅考虑飞行器平直飞与俯仰情况，油箱姿态变化示意图如图2 所示。

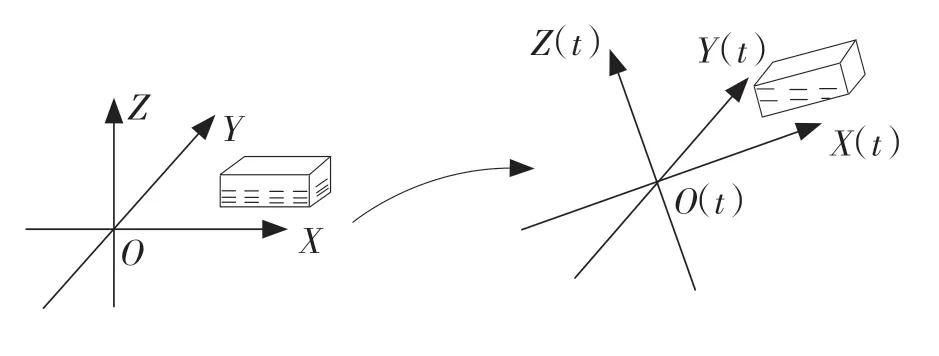
图2 油箱姿态变化示意图Fig.2 Schematic diagram of fuel tank attitude change

1.3 坐标系规定

（1）惯性坐标系O-XYZ：在地面上时，以空载飞行器的质心为原点O，飞行器纵向中心轴为X轴（水平方向），以飞行器前方为正向，重力方向的反方向为Z轴正向，通过右手法则确定Y轴；

（2）飞行器坐标系O（t）-X（t）Y（t）Z（t）：在t时刻，以空载飞行器质心位置为原点O（t），飞行器纵向中心轴为X（t）轴，以飞行器前方为正向，Y（t）轴垂直于X（t）轴所在的飞行器纵剖面，且O（t）-X（t）Y（t）组成右手坐标系，通过右手法则确定Z（t）轴；

（3）飞行器t时刻俯仰角：飞行器坐标系O（t）-X（t）Y（t）Z（t）中的X（t）轴与惯性坐标系O-XYZ中O-XY水平面的夹角，X（t）轴正方向在重力方向分量与重力方向相反时为正。

各约束条件及后文公式涉及的符号含义如表1。

表1 符号说明Tab.1 Symbol description

（续表）

2 数据集说明与3 种多约束条件质心平衡优化要求

2.1 数据说明

2.2 3 种多约束条件供油策略优化要求

（1）在满足飞行约束条件（1）-（7）时，已知各油箱的供油速度与飞行过程中的仰俯角度变化数据，求解该飞行器在此次执行任务过程中的质心变化曲线；

（2）在满足飞行约束条件（1）-（6）时，已知某次飞行任务飞行器的计划耗油速度数据，以及飞行器在飞行器坐标下的理想质心位置数据。若飞行器始终保持平飞（俯仰角为0），求解飞该次任务中的供油策略，使得飞行器瞬时质心位置与理想质心位置的欧氏距离的最大值达到最小，即

（3）在满足飞行约束条件（1）-（6）时，在各油箱初始油量未知的情况下，已知飞行器的计划耗油速度数据与在飞行坐标系下的理想质心位置数据，求解该次任务中各油箱的初始载油量及供油策略，并保证本次任务结束时各油箱剩余燃油总量不少于1 m3，并且使得飞行器瞬时质心位置与理想质心位置的欧氏距离的最大值达到最小，即

3 基于贪心算法与LDM-PSO 算法的质心平衡供油策略基本原理

3.1 贪心算法

3.1.1 贪心算法基本原理

贪心算法（又称贪婪算法）：贪心选择性质是指所求解问题的整体最优解可以通过计算一系列局部最优的选择，做选择时，只考虑对当前问题最佳的选择便是贪心选择。当求解问题的最优解包括其子问题的最优解时，则此问题具有最优子结构性质，这是可用贪心算法求解的关键特征。

已知飞行器的计划耗油数据，根据已有的约束条件，可得每次供油的油箱个数n和单个油箱的供油速度上限Ui（Ui＞ 0），因此将飞行器供油策略问题转化为每一时刻供油油箱选择的局部最优解问题，这正是贪心算法的优势。通过算法计算得到每一时刻满足所有约束的解，经过多次迭代获得近似最优解。

3.1.2 贪心算法求解流程

使用MATLAB 求解，贪心算法求解供油油箱顺序最优解流程图如图3 所示，贪心算法求解供油速度最优解流程图如图4 所示。

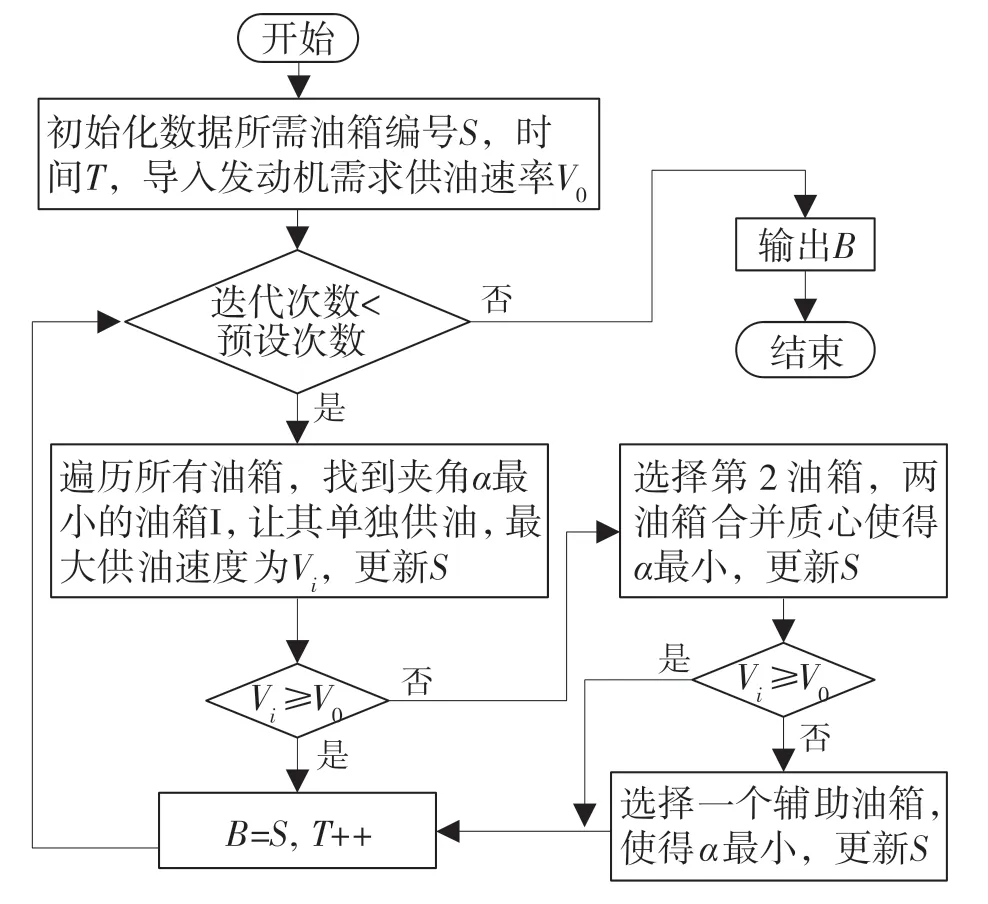
图3 求解供油油箱选择最优解流程图Fig.3 Flow chart of optimal solution for selection of fuel supply tank

图4 求解供油速度最优解流程图Fig.4 Flow chart of optimal solution for oil supply speed

3.2 LDM-PSO 算法

3.2.1 LDM-PSO 算法的基本原理

粒子群算法（PSO）：首先初始化一群随机粒子（随机解），然后粒子们就追随当前的最优粒子在解空间内搜索，即通过迭代找到最优解。假设d维搜索空间中的第i个粒子的位置和速度分别为Xi=（xi，1，xi，2，…，xi，d）和Vi=（vi,，1，vi，2，…，vi，d），每一次迭代粒子都通过跟踪两个最优解来更新，第一个是粒子本身所找到的最优解，即个体极值pbest，Pi=（pi,1，pi,2，…，pi,d）；另一个是整个种群目前找到的最优解，即全局最优解gbest，Pg。

较大的惯性因子有利于跳出局部极小点，便于全局搜索，而较小的惯性因子则有利于对当前搜索区域进行精确局部搜索，以利于算法收敛，所以本题采用线性权重递减的粒子群算法(LDM-PSO)，此算法采用线性变化的权重，让权重从最大值ωmax线性减小到最小值ωmin。

3.2.2 LDM-PSO 算法的求解流程

使用MATLAB 软件求解，LDM-PSO 算法求解最优解流程图如图5 所示。

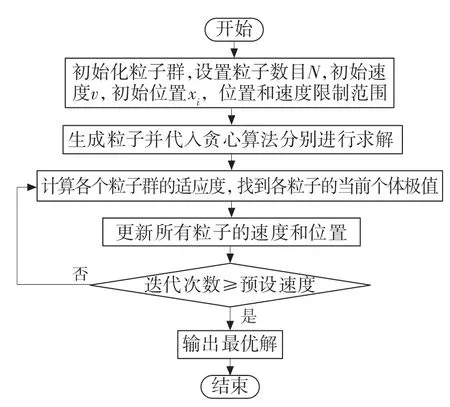
图5 LDM-PSO 算法流程框图Fig.5 Block diagram of LDM-PSO algorithm flow

4 3 种多约束条件质心平衡优化结果

4.1 第1 种多约束条件供油策略优化求解

4.1.1 模型建立

在飞行器平飞时，以O点作为原点建立平面直角坐标系xoz,液面纵坐标设为h,通过题目所给油液密度和某时刻油液质量,可计算油液的纵向截面面积Si；

如图6（b）所示，划分2 块区域S1、S2，它们的大小由式（2）求出：

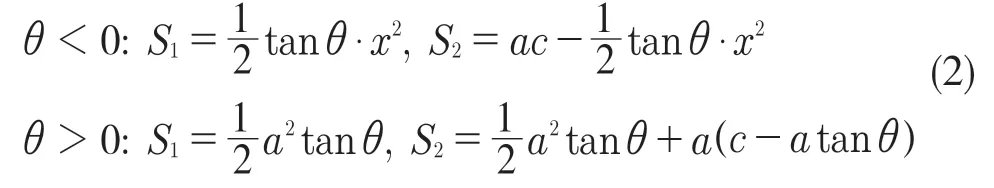
图6 飞行器油箱燃油液面临界图Fig.6 Critical diagram of fuel level of aircraft fuel tank

比较Si与S1，S2的关系，得到：（1）Si＜S1；（2）S1＜Si＜S2；（3）S2＜S1三种情况[4]；

（1）当油箱内油量较少时，即Si＜S1，油箱截面如图7所示，此时油箱质心坐标表达式如式（3）：

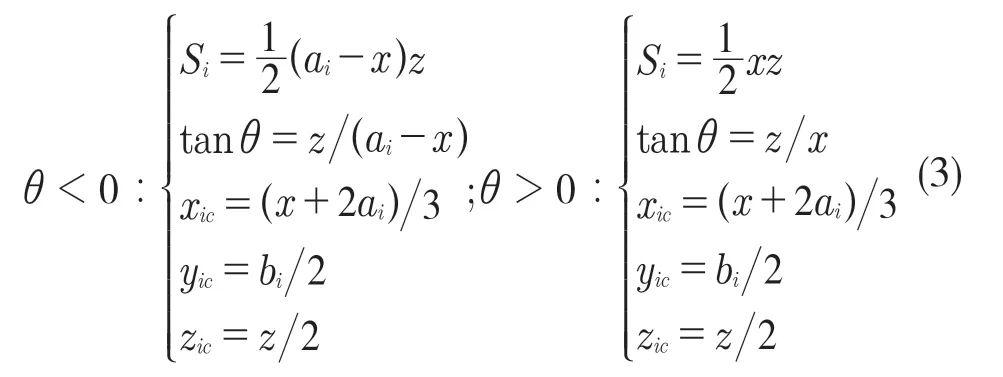
图7 油量较少时油箱截面示意图Fig.7 Section diagram of fuel tank with small amount of fuel

（2）当油箱内油量适中时，即，S1＜Si＜S2，油箱截面示意图如图8 所示，此时油箱质心坐标表达式如式（4）；

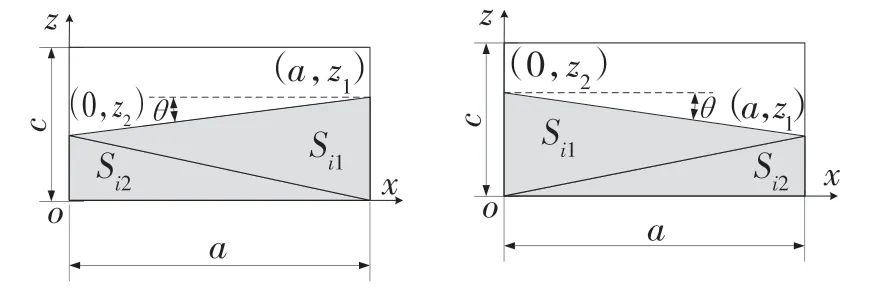
图8 油量适中时油箱燃油液面临界图Fig.8 Critical diagram of fuel level in fuel tank with moderate amount of fuel

（3）当油箱内油量较多时，即,Si＞S2，油箱截面示意图如图9 所示，此时油箱质心坐标表达式为式（5）；

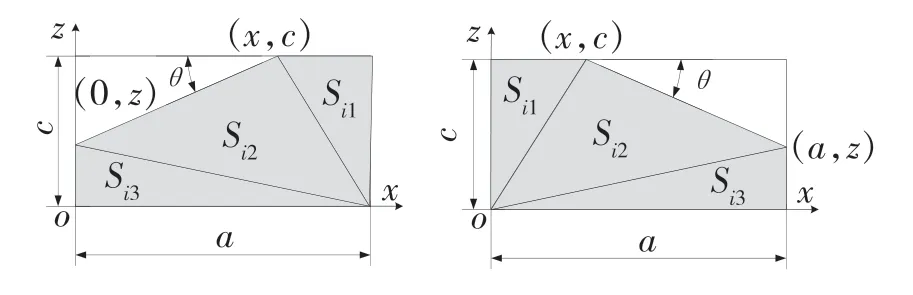
图9 油量比较多时油箱燃油液面临界图Fig.9 Critical diagram of fuel level in fuel tank with relatively high amount of fuel

求得各油箱质心坐标后，通过质心坐标变换，将其转换到飞行器坐标系中，此时6 个油箱的质心坐标如式（6）：

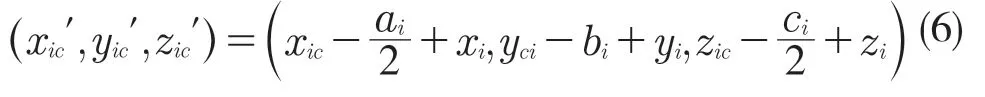
总质心坐标（xc，yc，zc）为：

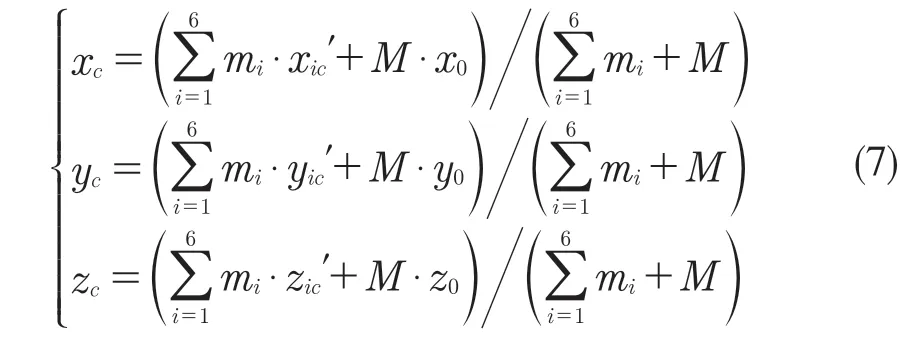
4.1.2 求解结果

根据程序流程图在 MATLAB 中编写程序并绘制飞行器质心轨迹曲线，如图10 所示，参考这条曲线可知本次飞行任务的供油策略是否合理，并为接下来的飞行任务中调整供油策略提供指导。其中质心坐标在x，y，z方向的变化如图11 所示[5]。

图10 质心的空间坐标曲线Fig.10 Spatial coordinate curve of the centroid

图11 质心坐标在x，y，z 方向的变化Fig.11 Changes of centroid coordinates in x,y and z directions

4.2 第2 种多约束条件供油策略优化要求求解

4.2.1 模型建立

设油箱编号为bi，供油速度为vi，其中bi与vi的对应关系为f，则实际质心坐标如式（8）：

因此，确定bi和vi即可求出实际质心坐标，将目标函数转化为围绕这2 个变量的函数：

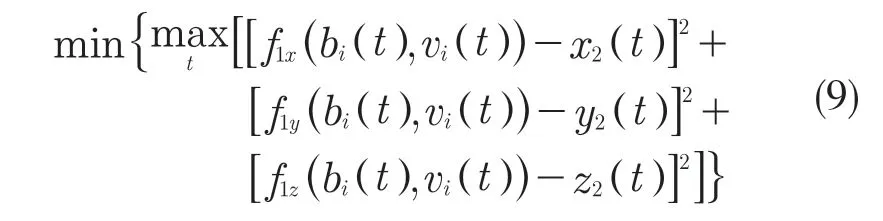
（1）确定供油油箱的编号bi（t）：

bi（t）可表示为bi（t）=Random(1,6)(t)，它需满足的约束条件是：

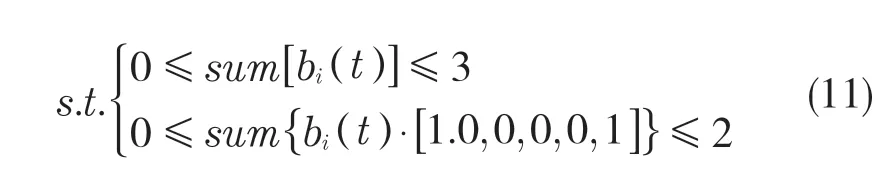
（2）确定油箱的供油速度vi：

在确定了供油油箱编号后，还需要确定与其对应的供油速度vi，已知t时刻发动机所需供油量为v0，两者需要满足的约束条件是：

综上所述，第2 种多约束条件供油策略优化要求的数学模型为式（9）、式（11）、式（12）。

4.2.2 求解结果

将飞行器供油策略问题转化为每一时刻的最优供油油箱选择的局部最优解问题，这正是贪心算法的优势[6]。实际油箱的供油速率分配如图12 所示，每一时刻实际质心与理想质心的偏移距离如图13所示。

图12 实际油箱的供油速率分配Fig.12 Distribution of fuel supply rate of actual fuel tank

图13 实际质心与理想质心的偏离距离Fig.13 Deviation distance between actual center of mass and ideal center of mass

4.3 第3 种多约束条件供油策略优化要求求解

4.3.1 模型建立

已知各油箱的油量初始量Vi=（V1，V2，…，V6），设实际质心与理论质心的距离为r。目标函数为：

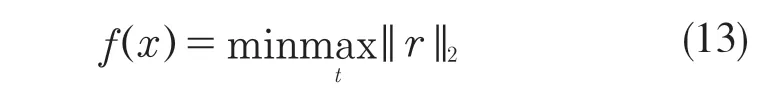
设在第2 种条件求解中程序的对应关系为f2（贪心算法），则每个粒子质心偏差值可表示为：

bi（t）可表示为bi（t）=Random(1，6)（t），它需满足的约束条件是：

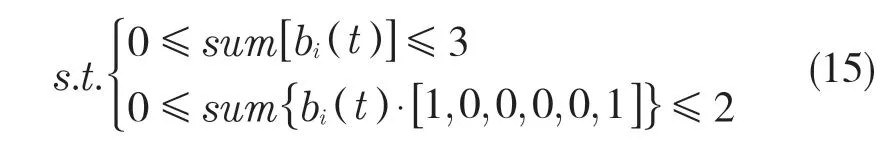
油箱的供油速度vi和发动机耗油速度v0两者之间需要满足以下约束：

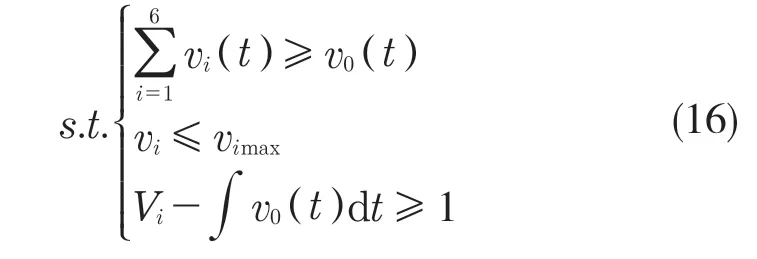
综上所述，第3 种多约束条件供油策略优化要求的数学模型为式（13）、式（15）、式（16）。

本问题通过改进权重的粒子群算法（LDMPSO），首先初始化一群随机粒子（随机解），然后粒子们追随当前的最优粒子在解空间内搜索，即通过迭代找到最优解[7]。在每一次迭代中，粒子通过跟踪2 个最优解来更新自己[8]，在找到最优值前粒子根据式（17）更新自己的速度和位置；

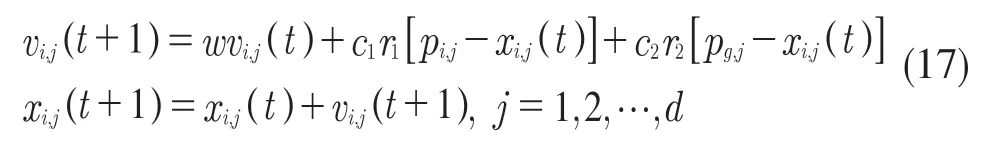
式中：w——惯性权重；c1，c2——正的学习因子；r1，r2——0 到1 之间均匀分布的随机数。

w随算法迭代次数的变化公式为：

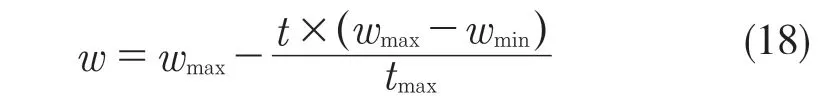
式中：wmax，wmin——w的最大值和最小值，本研究取wmax=0.9，wmin=0.4；t——当前的迭代次数；tmax——最大迭代步数。

4.3.2 求解结果

通过改进权重的粒子群算法（LDM-PSO），根据算法及程序流程图在MATLAB 中编写程序分别求得本次飞行任务中飞行器质心在x、y、z轴的偏移曲线如图14 所示，飞行器各油箱的实时剩余油量曲线如图15 所示。

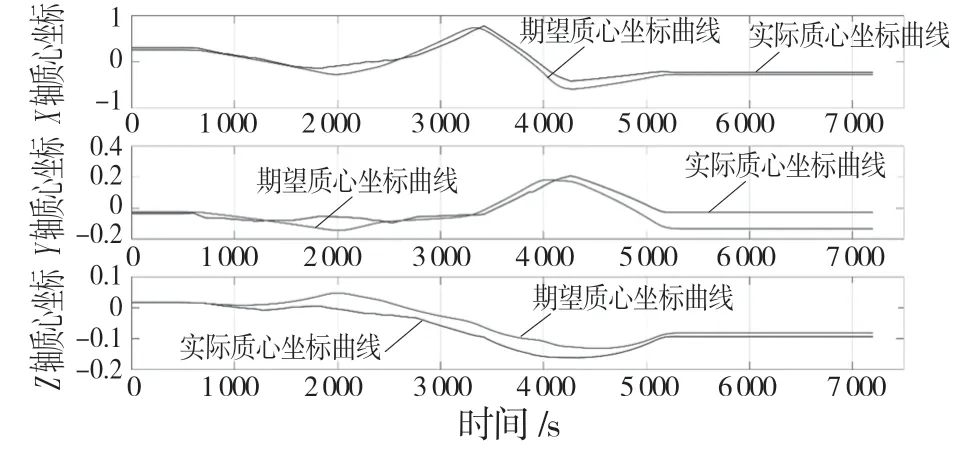
图14 飞行器质心坐标在x,y,z 轴的偏离曲线Fig.14 Deviation curve of spacecraft's center of mass coordinates on x,y,and z axes

图15 飞行器各油箱的实时剩余油量曲线Fig.15 Real-time remaining fuel volume curve of each fuel tank of the aircraft

5 结论

通过对某飞行器在多约束条件下的分析与建模，结合贪心算法与LDM-PSO 算法，实现了飞行器质心平衡供油策略的优化研究。本文针对3 种不同的多约束要求进行了验证分析，3 种供油策略规划的难度逐渐加大。求解结果表明，本算法能够有效解决不同约束条件下飞行器的质心平衡供油策略优化。有效解决了不同初始条件下飞行器因为质心变化而影响到对飞行器姿态控制的问题。本文所建立的算法有效地解决了遍历规划的运算复杂性问题，可以为飞行器质心平衡供油策略规划提供有价值的参考。