一字槽柱面气膜两种参数拟合优化分析

许冬伟，刘美红，孙军锋，赵超越

（650500 云南省 昆明市 昆明理工大学 机电工程学院）

0 引言

柱面气膜密封是依靠动静环之间的偏心所形成楔形间隙以及动静环上加工的均匀分布的动压槽产生的动压效应实现的密封。影响气膜密封性能的参数包括气膜的结构参数以及气膜运行时设置的操作参数。目前研究的气膜密封结构中，最典型的动压槽型为螺旋槽，选取螺旋槽的螺旋角为90°时，即为矩形直槽，也称为一字槽[1-3]。一字槽气膜中的每一个槽型结构左右对称，并且适应双向旋转。柱面气膜密封加工时需要动环转子与加工刀具同时进给，槽尺寸较小，加工困难，而螺旋槽加工更为困难，实际生产中很难得到应用。一字槽柱面气膜密封槽加工相对容易，加工成本相对较低[4]。陆俊杰[5]等通过建立气膜雷诺方程和膜厚函数数值模型，与实验进行对比得出直槽浮动性好于斜槽，并在此基础上肯定了一字槽槽型结构的优点。对于柱面气膜密封，研究者从各种槽型出发，寻求各种槽型柱面气膜密封特性。丁雪兴[6]等、马纲[7]等对不同槽型结构或稳态和动态性能进行分析优化，得到最佳结构及密封性能。马利军[8]等使用Fluent软件与实测结果对比进行正确性验证。结果表明，过大和过小的操作压力和径向间隙不利于浮环上浮。也有学者以气膜密封的密封性能为目标函数，采用各种优化算法进行优化，达到所设自变量的最优化。赵亚飞[9]、富影杰[10]等分别采用正交试验法和单一变量法在Fluent 软件中进行数值模拟，采用回归方程和最小二乘法拟合分析泄漏量或气膜刚度目标函数并进行优化；丁雪兴[11]、陈涛[12]等通过PH 线性方法、迭代法求解螺旋槽稳态流动场的非线性雷诺方程、坐标轮换法和区间递减法结合的优化算法建立多目标优化函数求解最佳槽参数。

目前，针对柱面气膜密封结构参数优化一般采用单一变量法，该方法忽略各结构参数的相互影响，所以对参数的优化有一定的局限性。而对于一字槽槽型结构的研究，王婷[13]等采用CFD 仿真方法定量分析气膜的结构参数、操作参数以及槽型参数对密封性能的影响，得到各参数取值范围。本文以一字槽柱面气膜模型进行研究，选取此参数范围对单一变量进行仿真，分析单一变量参数气膜的转速、压差、槽数、槽深、偏心率以及槽长宽比对浮升力与泄漏量比值、气膜刚度与泄漏量比值的影响曲线，得到在一定工况下的最佳参数。

1 柱面气膜流场数值分析

1.1 几何模型及仿真前处理

柱面气膜密封结构主要由动环、静环以及密封支撑座等零件组成，如图1 所示。静环由密封支撑座支撑固定，动环转子上带有直槽并与静环之间存在偏心结构，而动环转子在动力驱动下高速旋转，与静环之间形成一层具有一定气体刚度的流体薄膜，在楔形间隙和高速旋转的共同作用下，在气体密封结构中产生动压效，形成高压区以阻隔内外区域气体流动，达成非接触密封效果。

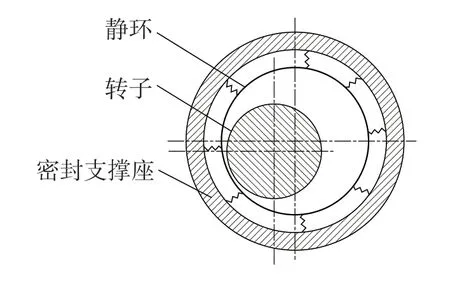
图1 柱面气膜密封结构示意图Fig.1 Schematic diagram of cylindrical gas film seal structure

用三维软件SolidWorks 建立动环转子和静环零件实体模型，设置模型尺寸：动环转子半径60 mm，静环内半径60.01 mm，静环周向长度40 mm，槽宽10 mm，槽深5～10μm，槽长5～25mm，槽数14～22个。静环与动环转子采用偏心位置安装，将此结构模型导入ANSYS Workbench 的DM 模块，抽取气膜模型。

设置入口为压力入口，出口为压力出口，动静环表面设置标准壁面边界条件，采用速度无滑移条件。将动环外表面设置为动壁面Moving-wall，静环内壁面设置为静壁面Stationary-wall，如图2所示。选用层流流动模型进行仿真[14]。

图2 气膜边界条件设置Fig.2 Gas film boundary condition setting

1.2 相关参数公式

泄漏量：

式中：Q——泄漏量；Rj——动环半径；p——气膜压力；θ——最大膜厚量起的角向坐标。

浮升力：

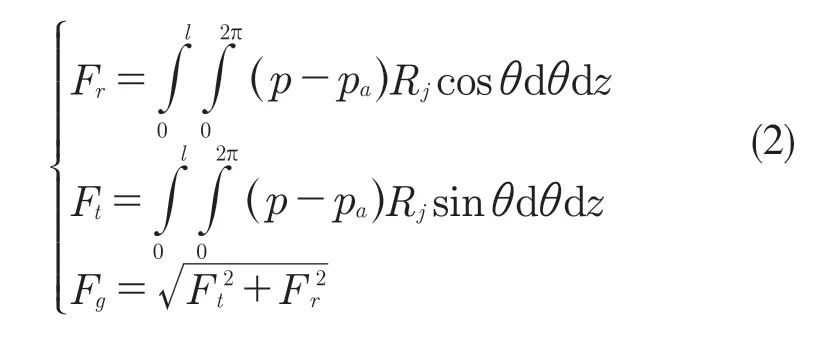
式中：Ft——浮环切向分量；Fr——浮环径向分量；Fg——浮升力合力。

气膜刚度：

式中：∂F——气膜内外壁面浮升力差值。

力漏比：

浮升力与泄漏量的比值。

刚漏比：

1.3 基本假设

（1）动静环之间间隙内气体为理想气体；（2）忽略流体的惯性力和流体的体积力；（3）气体分子与动静环之间无相对滑移；（4）假设动静环为刚体；（5）忽略动静环运行过程中的干扰，保持运行过程中的稳定状态。

1.4 网格处理

柱面气膜为一层微米级薄膜，而气膜轴长长度为毫米级，模型尺寸跨度较大。同时，气膜采用偏心结构，气膜沿轴向方向上厚度分布不均匀，不满足周期性边界条件，不能采用一部分模型进行仿真，因此网格划分为本模型研究的难点。本文使用ANSA 网格划分软件，将气膜整体模型分块划分，采用面映射网格map 划分面网格，在厚度方向上用体映射网格map 命令进行气膜整体结构网格划分，并对网格质量进行检验。

1.5 求解方法

在流体计算中采用压力速度耦合中SIMPLE 算法，控制方程采用二阶迎风离散格式。

2 求解结果及优化

本文从浮升力、泄漏量及气膜刚度参数进行气膜密封性能分析。浮升力为动静环之间形成气膜的支撑力，用于支撑静环形成动静环的非接触结构；泄漏量指气体经此密封而泄漏的气体量；气膜刚度则是气体形成气膜的本身特性。通常情况下，浮升力越大，泄漏越小，气膜刚度越大，气膜密封性能越好，所以设置力漏比和刚漏比，分析转速、压差、槽数、槽深，偏心率等参数影响下的变化规律。

2.1 力漏比的拟合曲线分析

图3（a）为转速对力漏比的影响曲线。设置转速从0～50 000 r/min，浮升力变化率为0.9%，泄漏量变化率为0.49%，均小于1%，可以忽略其变化，认为其保持稳定状态。转速增加，气膜的最大压力增加，随着高压到低压区压力变化，浮升力高压区域面积小于低压区面积，形成浮升力随转速增加而减小。转速对泄漏量的影响曲线类似于转速对浮升力的影响。泄漏量为动静环之间气体流出的量，当转速增大，气体动压效应增大，会阻止气体的流出，所以泄漏量随转速的增大而减小。为更好地分析转速对气膜密封的影响，选取力漏比分析转速的影响，曲线随着转速的增加先增大后减小。由拟合曲线可以看出，在35 000 r/min 时，力漏比取值最大。选取局部最优转速为35 000 r/min。图3（b）为压差对力漏比的影响曲线。由曲线可以看出，压差在0.1～0.2 MPa 时，力漏比的变化率最大，下降最快，浮升力变化比泄漏量变化小；随着压差的逐渐增大，力漏比曲线逐渐减小，最后趋于稳定，浮升力相对泄漏量变化率相同。选取局部最优压差为0.4 MPa。图3（c）—图3（f）分别为槽数、槽深、偏心率及槽长宽比对力漏比的影响曲线。设置槽数在14～22 范围，由图3（c）可知，随着槽数的增加，力漏比呈3 次拟合曲线缓慢减小。选取槽数参数局部最优为18。由图3（d）可知，槽深在5～7μm 时，力漏比曲线下降趋势最大，浮升力变化相对泄漏量变化小；当槽深逐渐增大，浮升力相对泄漏量的变化率缓慢减小。选取局部最优槽深参数为7μm。偏心率从0.3%变化到0.8%，在0.7%～0.8%时浮升力变化率为0.02%。由图3（e）知，偏心率在0.3%～0.4%时，力漏比拟合曲线的斜率小，在0.4%～0.8%时，力漏比拟合曲线的斜率变化稳定，力漏比值逐渐减小。选取局部最优偏心率参数为0.4%。分析槽大小对浮升力的影响，将槽的长、宽同时改变，得到一组长宽比值。如图3（f）所示，拟合曲线呈5 次函数曲线趋势减小，在长宽比为1.8时变化稳定，选取局部最优长宽比为1.8。

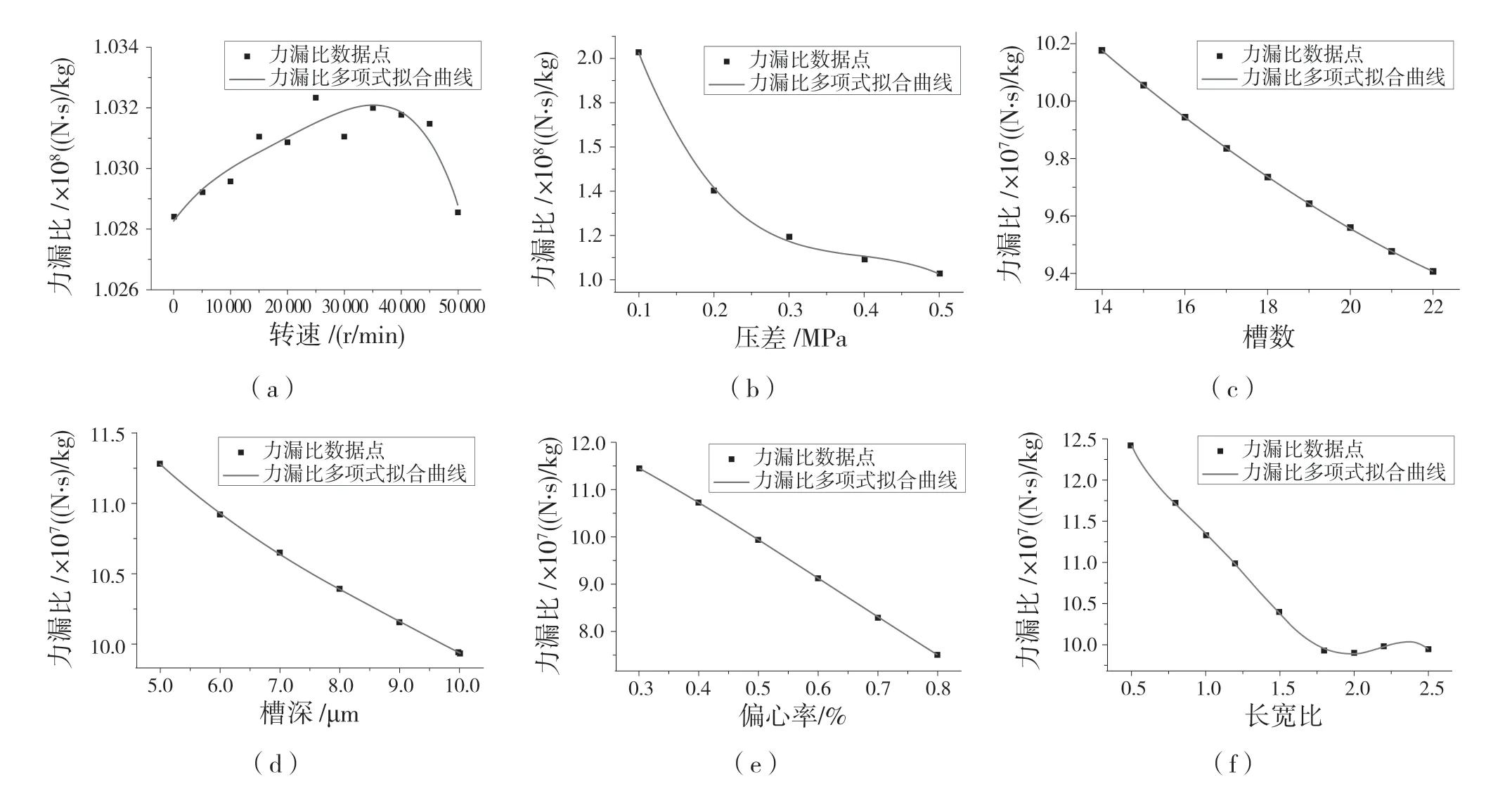
图3 力漏比影响曲线Fig.3 Force-to-leak ratio influence curve

通过分析力漏比在转速、压差、槽数、槽深、偏心率及槽长宽比等因素变化下的影响曲线，转速因素影响下，力漏比拟合曲线呈先增加后减小变化；压差、槽数、槽深及偏心率的力漏比拟合曲线均呈3 次函数趋势减小。槽长宽比的力漏比拟合曲线呈5 次函数趋势下降，在1.8 时变化趋于平稳。根据图3 各曲线分析，选取各影响参数的最优值为：转速为35 000 r/min，压差为0.4 MPa，槽数为18，槽深为7 μm，偏心率为0.4，槽长宽比为1.8。

2.2 刚漏比拟合曲线分析

图4（a）为转速对刚漏比的影响曲线。设置转速从0～50 000 r/min，气膜刚度变化率为0.38%，小于1%，转速对气膜刚度和泄漏量的影响均较小。转速增加，浮升力下降，而气膜刚度为浮升力对气膜平均刚度的微分，所以气膜刚度的变化趋势与浮升力变化趋势类似。泄漏量各点数据随着速度变化保持在一条水平线上，表明在转速不断变化的工况下，泄漏量几乎保持不变。随着转速的增加，泄漏量缓慢减小，其变化率0.49%，小于1%，可以忽略转速对泄漏量的影响。转速对气膜刚度和泄漏量的影响均较小。为更好地分析转速对气膜密封的影响，选取刚漏比分析转速对它的影响。当气膜刚度增大，泄漏量减少，分析刚漏比拟合曲线相邻点之间的最大变化率，刚漏比曲线随着转速的增加而增大，40 000 r/min 时，刚漏比值达到最大。选取局部最优转速为40 000 r/min。图4（b）为压差对刚漏比的影响。由曲线可见，压差在0.1～0.2 MPa时，刚漏比拟合曲线的变化率最大，下降最快，气膜刚度变化比泄漏量变化小；随着压差的逐渐增大，刚漏比拟合曲线逐渐减小，最后趋于稳定，气膜刚度相对泄漏量变化率相同。选取局部最优压差为0.4 MPa。图4（c）—图4（f）分别为槽数、槽深、偏心率及槽长宽比对刚漏比的影响曲线。设置槽数在14～22 范围，由图4（c）可知，随着槽数的增加，刚漏比拟合曲线呈3 次曲线趋势缓慢增长，说明随着槽数的增加，气膜刚度与泄漏量相对变化率较大。选取槽数参数局部最优为22。槽深由5μm 增长到10μm 时，由图4（d）可见，刚漏比拟合曲线呈2 次曲线趋势增长，气膜刚度变化相对泄漏量变化大；当槽深逐渐增大，气膜刚度相对泄漏量的增长趋势变缓。选取局部最优槽深参数为10μm。偏心率从0.3 变化到0.8，由图4（e）知，偏心率在0.3～0.4 时，刚漏比拟合曲线的斜率小，在0.4～0.8 时，刚漏比拟合曲线的斜率变化稳定，刚漏比值逐渐减小。选取局部最优偏心率参数为0.4。分析槽大小对气膜刚度的影响，由图4（f）可知，拟合曲线呈5 次函数曲线趋势增大，在长宽比为1.8 时变化稳定。选取局部最优长宽比为1.8。

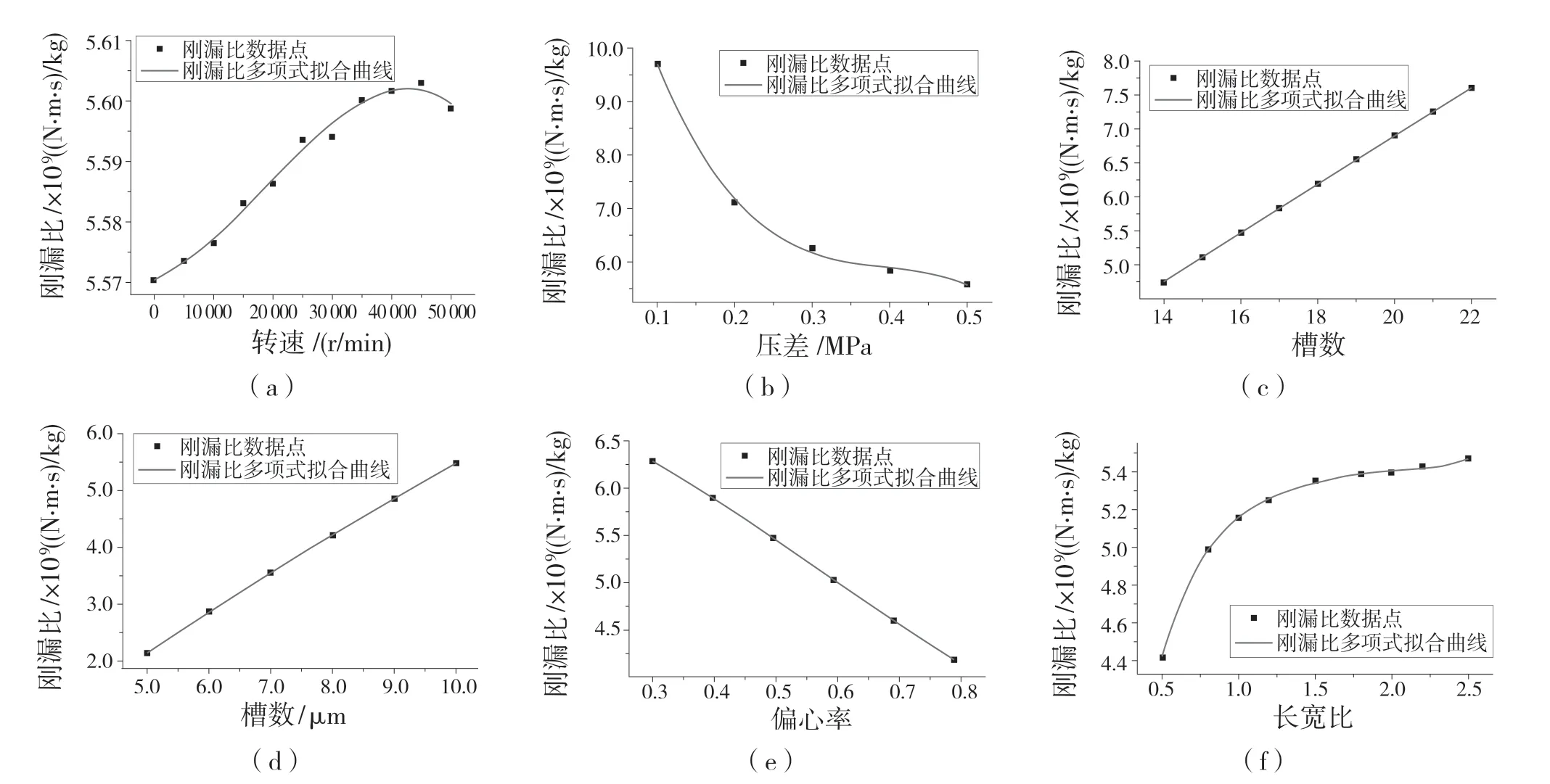
图4 刚漏比影响曲线Fig.4 Stiffness-to-leak ratio influence curve

分析刚漏比在转速、压差、槽数、槽深、偏心率及槽长宽比等因素变化下的影响曲线。转速因素影响下，气膜刚度变化大于泄漏量变化，曲线呈非线性曲线规律变化；压差影响下，刚漏比拟合曲线呈4 次函数趋势减小，气膜刚度增长小于泄漏量增长；槽数、槽深及偏心率的刚漏比曲线中，槽深、槽数因素均随着参数的增加而增长，气膜刚度增长趋势大于泄漏量增长趋势，偏心率随着参数的增加呈2 次函数趋势减小，气膜刚度增长趋势小于泄漏量增长趋势。槽长宽比拟合曲线呈五次函数趋势上升，在1.8 时变化趋势平稳。根据图4 各曲线分析，选取各影响参数的最优值为：转速40 000 r/min，压差0.4 MPa，槽数22，槽深10 μm，偏心率为0.4,槽长宽比为1.8。

2.4 数值模拟

采用Fluent 流场仿真软件，针对上述力漏比、刚漏比2 种参数曲线分析得出的转速、压差、槽数、槽深、偏心率及槽长宽比优化参数进行数值计算。第1 种优化参数由力漏比拟合曲线得出的优化参数，转速为35 000 r/min，压差为0.4 MPa，槽数为18，槽深为7μm，偏心率为0.4，槽长宽比为1.8；第2 种优化参数为刚漏比曲线得出的优化参数，转速为40 000 r/min，压差为0.4 MPa，槽数为22，槽深为10 μm，偏心率为0.4，槽长宽比为1.8。

图5 为2 种优化参数的柱面气膜静压力云图。由图5 可见，高压区出现在由偏心形成的动压处，在槽区的影响，最大压力出现在槽台一侧，这是由于流体旋转时槽台阻挡气流形成高压。通过流体仿真软件Fluent 进行气膜流场数值计算，计算2 种参数模型的力漏比与刚漏比数值，第1 种优化参数模型的力漏比和刚漏比数值均优于第2 种优化参数得出的数值。

图5 优化参数压力云图Fig.5 Optimized parameter pressure cloud chart

3 结论

转速、压差、槽数、槽深及偏心率等因素对浮升力、气膜刚度和泄漏量密封性能的变化率不同，当力漏比、刚漏比曲线上升，浮升力、气膜刚度相对于泄漏量增长较快，反之则相反。

综合考虑上述力漏比、刚漏比曲线，获得一字槽柱面气膜密封最佳匹配参数为转速35 000 r/min，压差为0.4 MPa，槽数为18，槽深为7 μm，偏心率为0.4，槽长宽比为1.8。