基于滑模控制的跟随车辆纵向研究
2022-10-31郑雁南
郑雁南
(201620 上海市 上海工程技术大学 机械与汽车工程学院)
0 引言
汽车行业在飞速发展的同时也引发了各种各样的社会问题[1]。能源消耗增加、道路交通状况恶劣,给人带来消极情绪,再加上机动车驾驶员数量剧增,驾驶员经验不足等因素都是导致交通事故的主要原因[2]。近年来智能交通逐渐进入人们的视野,智能车辆是智能交通中的重要组成部分[3],具有人机交互界面,能够感知周围环境,根据信息规划路径,并且通过集成控制系统执行,从而完成车辆路径跟踪控制[4]。
本文通过建立智能车辆列队模型,对滑模纵向控制算法研究,设计控制器对期望路径进行跟踪。为了验证滑模纵向控制器的控制效果,将其与PID传统控制进行对比,先建立车身纵向动力学模型、轮胎纵向动力学模型、车辆空气动力学以及横纵向动力学模型,通过后车与前车保持间距的方式验证纵向控制的控制效果。为此,建立了车辆列的跟随模型,以领航车辆和跟随车辆间距与预期间距的误差作为纵向控制器的控制效果。
1 车辆纵向动力学理论
在智能车辆纵向跟踪控制中,车辆纵向运动学模型在车辆缓慢行驶时对车辆纵向控制的影响较大,而车辆动力学模型在车辆高速行驶或复杂交通情况下对车辆纵向控制的影响比较大。设计控制算法时,需要在车辆动力学模型基础上进行设计和研究,同时兼顾运动学模型[5]。
1.1 车身纵向动力学模型
对车身进行纵向坡道受力分析。如图1 所示,车辆受到自身重力,同时4 个轮胎有轮胎法向力,驱动系统给车辆的驱动力具体表现在4 个轮胎与地面的接触点上轮胎对地面的摩擦力,使其纵向运动同时也受到了与运动方向相反的风力以及车轮滚动时受到的滚动阻力。
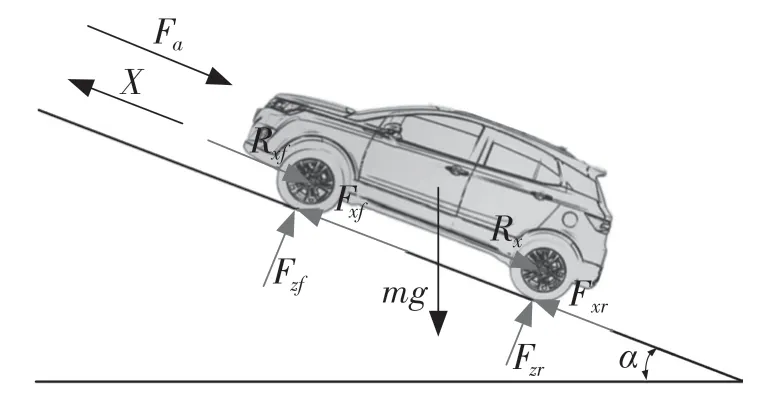
图1 车辆在坡道受力分析图Fig.1 Stress analysis diagram of vehicle on ramp
根据牛顿第二定理,可建立车辆在X方向纵向动力学平衡表达式为:

驱动力表达式为:

式中:m——车辆的质量,kg;——车辆沿X方向的加速度,m/s2;Fxf,Rxf——前轮的纵向力和滚动造成的阻力,N;Fxr,Rxr——后轮的纵向力和滚动造成的阻力,N;g——重力加速度,m/s2;Fα——空气阻力,N;α——地面坡度,rad。
1.2 轮胎纵向动力学模型
如图1 所示,车辆行驶过程中,在法向力作用下,轮胎与地面接触点会发生形变,随着轮胎的滚动接触点变化,离开接触点的形变恢复,此时消耗的能量成为滚动阻力[6]。轮胎的纵向驱动力是车辆前进的关键所在,它通过轮胎滚动与地面相互作用产生摩擦力,与地面和轮胎的摩擦系数有关。此时,轮胎法向力、滑移率、地面摩擦系数都对轮胎产生的纵向驱动力产生影响,车辆在驱动过程中,滑移率表达式为:
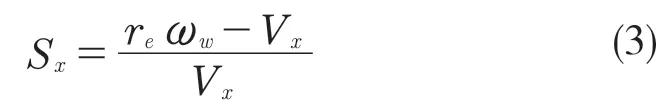
车辆制动过程中,滑移率的表达式为:
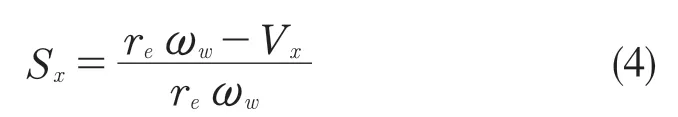
当接近纯滚动状态下,前后轮的纵向驱动力可表示为:

式中:Sx——车辆滑移率;r——轮胎半径,m;Cr——后轮侧偏刚度,N/rad;ω——轮胎运动的角速度,rad/s;Vx——车辆向X方向运动的纵向速度,m/s;Cf——前轮侧偏刚度,N/rad。
滚动阻力与轮胎法向力有关,表达式为:
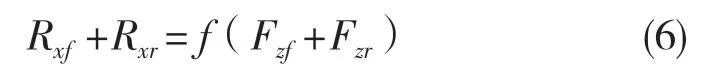
式中:Fzf,Fzr——前轮、后轮的法向力,N;f——车轮的滚动阻力系数。
轮胎的法向力表达式为:
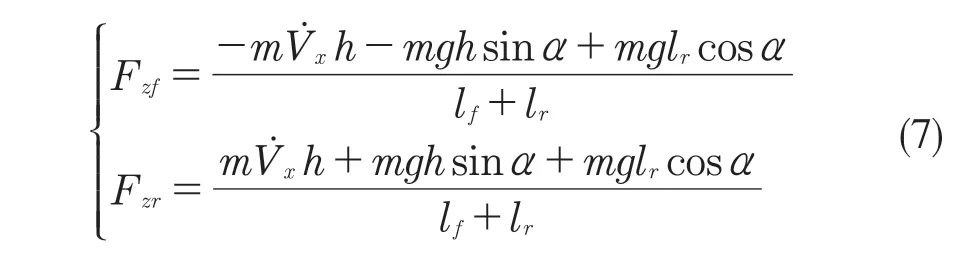
式中:lf,lr——车辆中心到前后轴的距离,m;h——车辆中心距离地面的高度 。
1.3 车辆空气动力学
在车辆行驶过程中伴随着空气流动,空气会对车辆的纵向运动产生一定的阻碍,车速越快,车辆受到的空气阻力越大,其关系式为:

式中:Vw——风速,m/s;A——车辆的迎风面积,即车体高度与宽度的乘积,m2;Cd——空气助力系数;ρ——空气密度。
1.4 车辆的纵向动力学模型
车身动力学、轮胎动力学以及空气动力学方程代入车辆动力学平衡方程,可得:
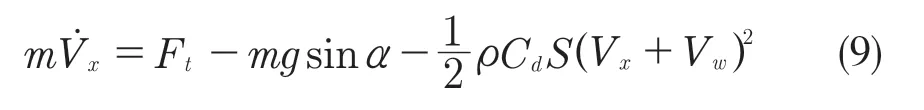
由力矩计算公式可得有关制动与驱动力矩的车辆动力学表达式:
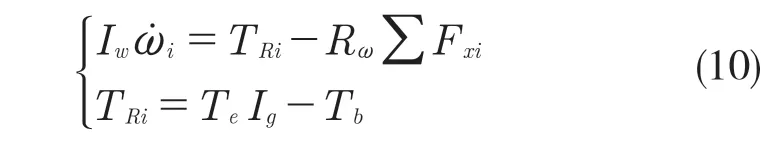
式中:Fxi——单个车辆轮胎附着力,是车辆质量与附着系数的乘积,N;Tb——制动器制动力矩,N·m;Rw——车轮滚动半径,车轮因承受载荷发生形变时接触点到轮胎中心的距离,m;ωi——轮胎转速,rad/s;Ig——传动比,即传动系统输出轴轮胎角速度的比值;Te——发动机曲轴端输出的力矩,N·m;Iω——轮胎转动惯量,不加制动盘、轮毂和轮胎组成,0.5~1.0 kg/m2;FRi——驱动力距,N·m。
假设车辆在纵向运动中轮胎一直处于纯滚动行驶状态,车辆的行驶速度为:

驱动力可表示为:

联立式(10)—式(12)可得:
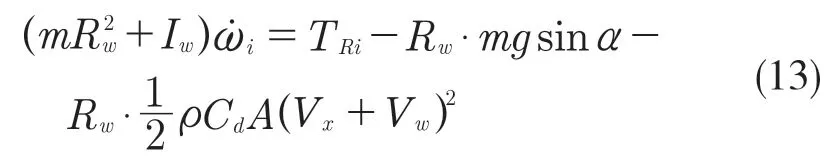
式(13)两边同时除以车轮滚动半径,可得纵向动力学模型:
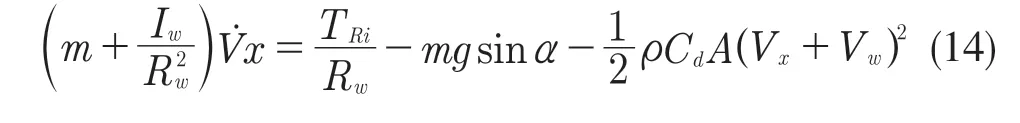
2 车辆列跟随模型的建立
车辆列跟随协同行驶是智能车辆实现无人驾驶的基本功能之一,对于车辆列中的任意2 个相邻车辆,根据位置不同分为领航车辆和跟随车辆,前车相对后车作为领航车辆。如图2 所示,假设车辆列跟随模型中的所有车辆都是相同型号,均使用本文设计的同一控制器,在下文的模拟中使用相同的模拟参数。
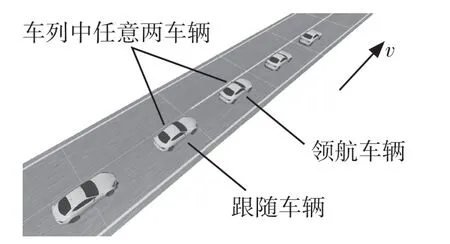
图2 多车辆跟随模型Fig.2 Multi-vehicle following model
在车辆列跟随模型系统中,这里不考虑车辆与车辆的通信,车辆只能通过感知系统传来的领航车辆位置信息作为跟随车辆的预期路径轨迹位置点,通过对单个车辆进行设计跟踪控制器,使其保持对前车的距离,且完成对前车的跟踪控制[7]。
为了提升安全性和乘坐舒适性,在预期路径行驶时,限制车辆的转向和制动以及油门动作,即当输出信号超过一定范围时,整个仿真停止即输出信号:

3 传统PID 纵向控制器设计与仿真
设计过程中,直线纵向控制效果不易评估,故在期望跟随路径中加入变道跟随路径,如图3 所示。不仅测试纵向控制器能力,还通过左右两个弯道验证横向车辆控制器和纵向控制器的耦合状况,并找出传统PID 纵向控制器的不足,为滑模纵向控制器设计提供借鉴。
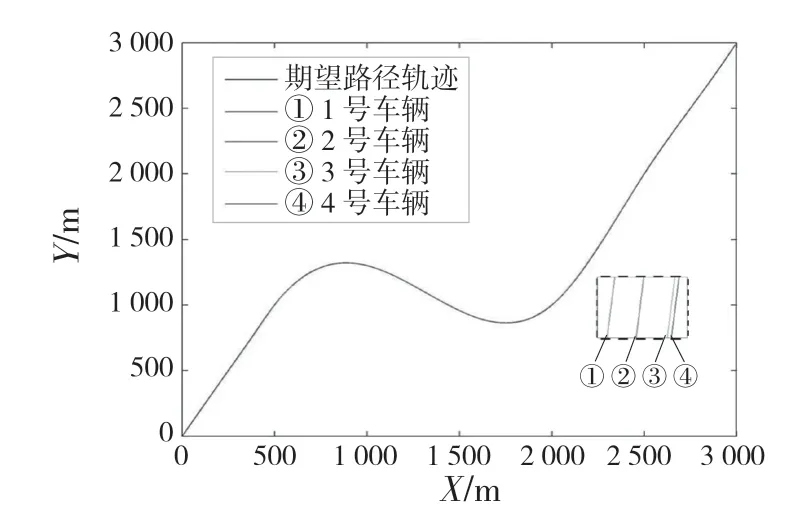
图3 期望路径轨迹图Fig.3 Expected path graph
由于加入了横向控制,需要改进横纵向控制下的车辆动力学模型,纵向加速度:
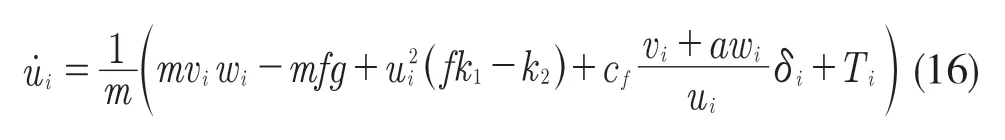
式中:ui——纵向速度,m/s;m——车辆质量,kg;vi——横向速度,m/s;wi——偏航率;f——轮胎摩擦系数;g——重力加速度,m/s2;k1,k2——空气的升力和阻力;Cf——前轮侧偏刚度;a——车辆中心到前轴距离;δi——车轮转向角;Ti——轮胎与地面接触点处的纵向力。
横向加速度:

式中:Cr——后轮侧偏刚度;b——车辆中心到后轴距离。
偏航率对时间求导:
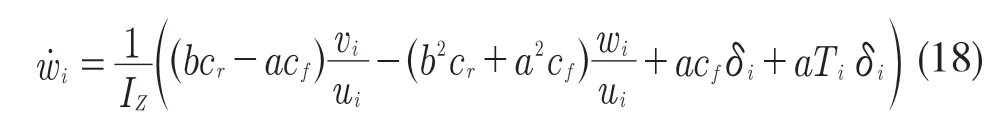
式中:IZ——车轮的转动惯量。
综上可得车辆纵向动力学表达式:
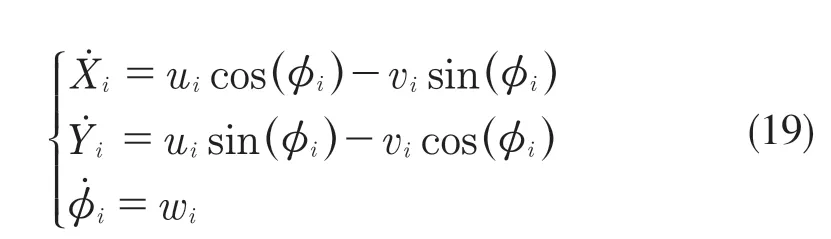
式中:Xi,Yi——车辆的X轴方向位置坐标和Y轴方向的位置坐标;φi——车辆的偏航角。
4 滑模纵向控制器设计与仿真
车辆纵向控制的目标是保持与前一辆车的期望安全距离。预设安全距离为10 m,为了使实际相对距离di等于期望的安全距离d0(i=0,1,2,3…),车辆选择的滑动变量是期望的安全距离d0与实际相对距离di之间的误差,误差表达式为:

车辆实际相对距离di的表达式为:

式中:xi-1,xi——第i-1 辆车与第i辆车的的实际纵向位置。
滑模纵向控制器需要针对弯道曲率大且无法很好跟随的情况设计出能够在极短时间内消除滑动变量的控制律,通过滑模控制方法,其滑模函数表达式为:

式中:r11,r12——滑模控制算法设计参数。
纵向滑模控制的控制律:
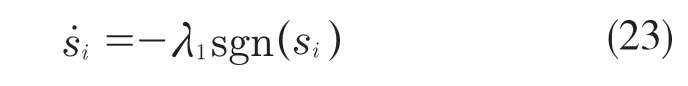
式中:λ1——调整乘客安全性和舒适性的设计参数。
对式(22)设计李雅普诺夫函数

式(24)对时间求导

结合式(23)可得
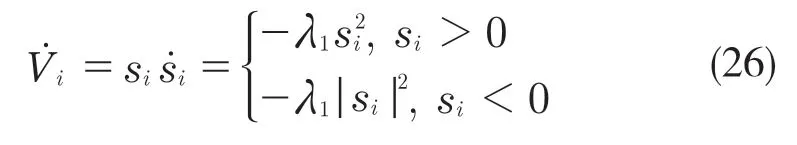
通过式(22)—式(26)可以让si在较短时间内趋向于滑模面,对式(22)求导可得

联立式(16)和式(28)可得第i辆车辆的控制律方程

为解决响应时间问题,由式(29)设计在短时间收敛的滑模纵向控制器。此外,还需设计控制器的稳定性。由车辆列在滑模面间距动力学模型可知,令si=0(i=1,2,3,…,N)可得

联立式(30)、式(31)可得间距误差关于滑模控制的表达式:
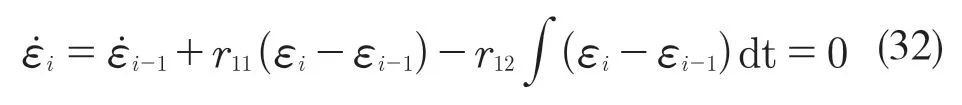
通过李雅普诺夫函数方法得出上述方程等于0的控制器的稳定性的条件:

由式(33)知,r11和r12均为正值时,滑模控制器对车辆列系统控制是稳定的。
5 仿真与结果分析
参考车辆仿真模型参数,车辆的初始位置和速度见表1。应用此车辆参数,对滑模纵向控制器对4 辆车的车辆列系统通过CarSim 与MATLAB/Simulink 联合仿真。

表1 车辆的X 轴与Y 轴初始位置、初始速度及初始偏航角Tab.1 Initial position and speed of X-axis and Y-axis and initial yaw angle of vehicle
仿真实验车辆列在道路上行驶时,用到的控制参数见表2。

表2 控制参数表Tab.2 Control parameters
传统PID 纵向控制和滑模纵向控制的车间距误差变化情况分别如图4、图5 所示。由图4 知,传统PID 纵向控制在车辆列启动、转弯过程中,车辆间距有较大误差。在道路曲率最大时,跟随车辆间距误差传递现象更加明显,误差最大达到2.5 m,且到达稳态的时间更长。
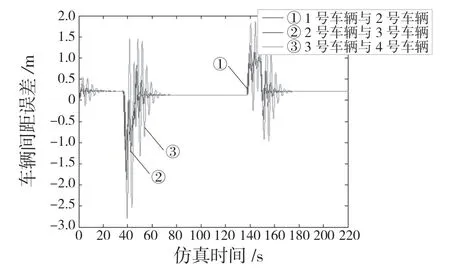
图4 传统PID 纵向控制下的车间距误差变化情况Fig.4 Variation of vehicle spacing error under traditional PID longitudinal control
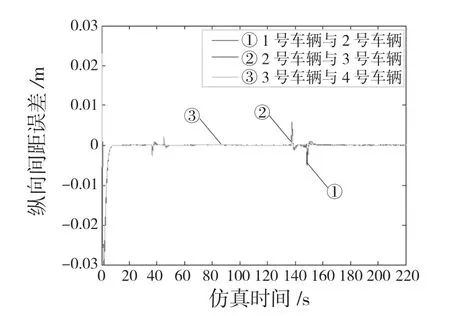
图5 滑模纵向控制下的车间距变化误差Fig.5 Variation error of vehicle spacing under sliding mode longitudinal control
由图5 知,滑模控制效果与PID 控制不同,最大间距误差出现在开始点,误差值最大为0.03 m,误差收敛稳态平衡点的速度得到显著提升。此外,收敛平衡点收敛在两辆车间距误差为零且没有出现误差传递现象,滑模纵向控制器稳定性表现良好,不仅控制了误差传递现象,还提高了收敛速度。
6 结论
为了提高智能车辆纵向控制精度,基于滑模控制设计纵向控制器,建立了车身纵向动力学模型、车辆动力学模型,并且通过后车与前车保持间距的方式验证纵向控制的控制效果,经过CarSim 与MATLAB/Simulink 联合仿真,滑模控制间距误差最大仅为0.03 m,误差收敛稳态平衡点的速度是PID控制的5 倍。此外,收敛平衡点收敛在两辆车间距误差为零且没有出现误差传递现象,控制器具有很强的稳定性。
