X 型支撑混凝土剪力墙抗震性能有限元分析

2022-10-29焦红部千王松岩

新型建筑材料 2022年10期

焦红，部千，王松岩

（山东建筑大学土木工程学院，山东济南 250101）

0 引言

型钢混凝土剪力墙具有强度高、刚度大、施工便利等优点，被广泛应用于高层建筑中，例如上海中心大厦、上海环球金融中心和深圳国际金融大厦等[1]。近年来，许多学者对型钢混凝土剪力墙进行了充分的研究。吕西林等[2]通过16个型钢混凝土剪力墙的拟静力试验，研究了该剪力墙的抗震性能，并建立了恢复力骨架曲线的数学模型。方明霁等[3]进行了4榀1/3～1/4缩尺模型的型钢混凝土剪力墙的拟静力试验，试验结果表明，型钢桁架剪力墙的耗能能力和承载力优于钢筋混凝土剪力墙。在竖向支撑的基础上，曹万林等[4-5]、张健伟等[6]发现，在钢筋混凝土内使用X型暗支撑使混凝土在整个试验过程中裂缝开展充分并且整体刚度降低缓慢，提升了混凝土结构的耗能能力和抗震能力。在此基础上，王玉镯等[7-9]使用槽钢、角钢和H型钢进行X型支撑，结果表明，型钢支撑混凝土剪力墙的刚度退化速率更加缓慢，而且中后期刚度明显优于无支撑试件。由此可见，X型支撑混凝土剪力墙具有良好的应用前景，但国内外对于X型支撑剪力墙的抗震性能研究较少，且主要针对不同类型的型钢和型钢尺寸进行试验研究，对于轴压比限值与高跨比的匹配关系尚不明确，抗剪承载力计算方法也鲜见报道，限制了该类剪力墙的设计与应用。

综上，为了推动该类组合剪力墙的研究及应用，本文使用ABAQUS有限元分析软件对文献[7]中的试件进行建模计算和验证，在综合试验结果和有限元模拟结果取得良好效果的基础上，通过17个试件的拓展分析，探讨了轴压比、剪跨比、型钢尺寸和型钢强度对X型支撑混凝土剪力墙抗震性能的影响规律，并针对不同剪跨比进行了近60个试件的试算分析，研究了轴压比限值与剪跨比的匹配关系，最后提出了抗剪承载力计算方法，旨在为丰富该结构的设计提供参考。

1 试验概况

选取文献[7]中X型支撑剪力墙试件进行建模计算，以验证模型的准确性。试件加载点至基础梁顶面高度为L=1400 mm，墙体内钢筋以A8@150双层双向布置，加载梁与地梁均配置6A22和A8@100。X型支撑在墙体中对角布置，为交叉焊接的I10型钢，形成一个整体，试件构造示意见图1[7]，试验结果见文献[7]。材料性能见表1。

表1 材料性能

2 有限元模型建立

2.1 材料属性

（1）混凝土

本文采用2020版ABAQUS中的混凝土塑性损伤模型（CDP），混凝土单元采用精度较高的三维八节点六面体C3D8R实体单元，本构关系取用GB 50010—2010《混凝土结构设计规范》中所提出的单轴受压应力-应变关系曲线：

式中：fc、εc——分别为混凝土极限压应力、应变；

αa、αd——分别为影响混凝土上升段和下降段形状的参数，按GB 50010—2010取用。

（2）钢材

型钢采用S4R壳单元，钢筋采用T3D2桁架单元，钢材本构关系采用双折线理想塑性模型[10]（见图2），即屈服前为理想弹性，屈服后到极限强度前的硬化刚度为钢材弹性模量的0.01。其中fa和εa为屈服应力和屈服应变；fu和εu为极限应力和极限应变；E0为弹性模量，Es为硬化刚度，Es=0.01E0。

2.2 相互作用

型钢与钢筋均“内置”于混凝土内部，忽略其与混凝土之间的粘结滑移。在加载梁顶部中心处设置参考点，并将参考点与加载板进行“耦合”，便于设置加载方式与边界条件。

2.3 边界条件及加载方式

根据试验情况，约束了试件下部3个方向的位移，但不约束转动，上部在加载点处施加恒定轴力和低周反复水平位移。

2.4 网格划分

经试算，混凝土采用50 mm尺寸网格、型钢采用20 mm尺寸网格时可以保证较高的计算精度及计算效率，建立的模型网格如图3所示。

2.5 模型验证

利用上述建模方法及材料属性对文献[7]中的X型支撑试件进行计算，所有试件试验及模拟的滞回曲线和骨架曲线对比如图4所示，破坏形态对比如图5所示。

由图4、图5可见，有限元模拟的滞回曲线与试验结果具有极高的吻合，加载刚度和卸载刚度一致，均呈现了相同的趋势和相似的破坏过程。剪力墙底部出现了与试验结果相同的水平损伤。但有限元模拟的滞回曲线更饱满，骨架曲线刚度较大，峰值点位移也更小，造成误差的原因主要为：（1）试验过程中试件并非完全固结，加载过程中夹具内有空隙而产生虚位移，试验结果的峰值点位移较大；（2）有限元分析模型忽略了钢筋和型钢与混凝土之间的粘结滑移，因此出现了一定过约束导致滞回曲线较试验结果更饱满。整体上看有限元结果和试验结果的极限承载力比值为1.061，初始刚度比值为1.038，本文建立的有限元模型得到验证，说明此模型能可靠地预测X型支撑型钢混凝土剪力墙的抗震性能。

2.6 应力分析

钢筋笼和型钢的塑性应变云图如图6所示。

由图6可见，钢筋笼的最大塑性应变出现在试件的中下部，这与X型钢的最大塑性应变区一致，并且型钢塑性应变集中在X交叉区域，表明该区域出现了较大的应力集中。

模拟试件纵筋、水平筋和型钢最大应力部位的应力变化如图7所示。

由图7可见，在试件加载过程中纵筋、水平筋和型钢都达到了屈服强度，表明其在试件经历地震作用下均发挥了作用。值得注意的是，在低周反复作用下，柱脚纵筋首先达到屈服，随后X型钢支撑的交叉区一侧出现屈服，并由下部屈服逐渐向交叉区扩散。这说明在后续的优化过程中，最重要的是提高X支撑下部的刚度与强度。

3 影响因素分析

基于已验证的几何模型和本构模型，以轴压比n、剪跨比λ、型钢尺寸和型钢屈服强度fa为变化参数设计了17个试件，试件参数及计算结果见表2。

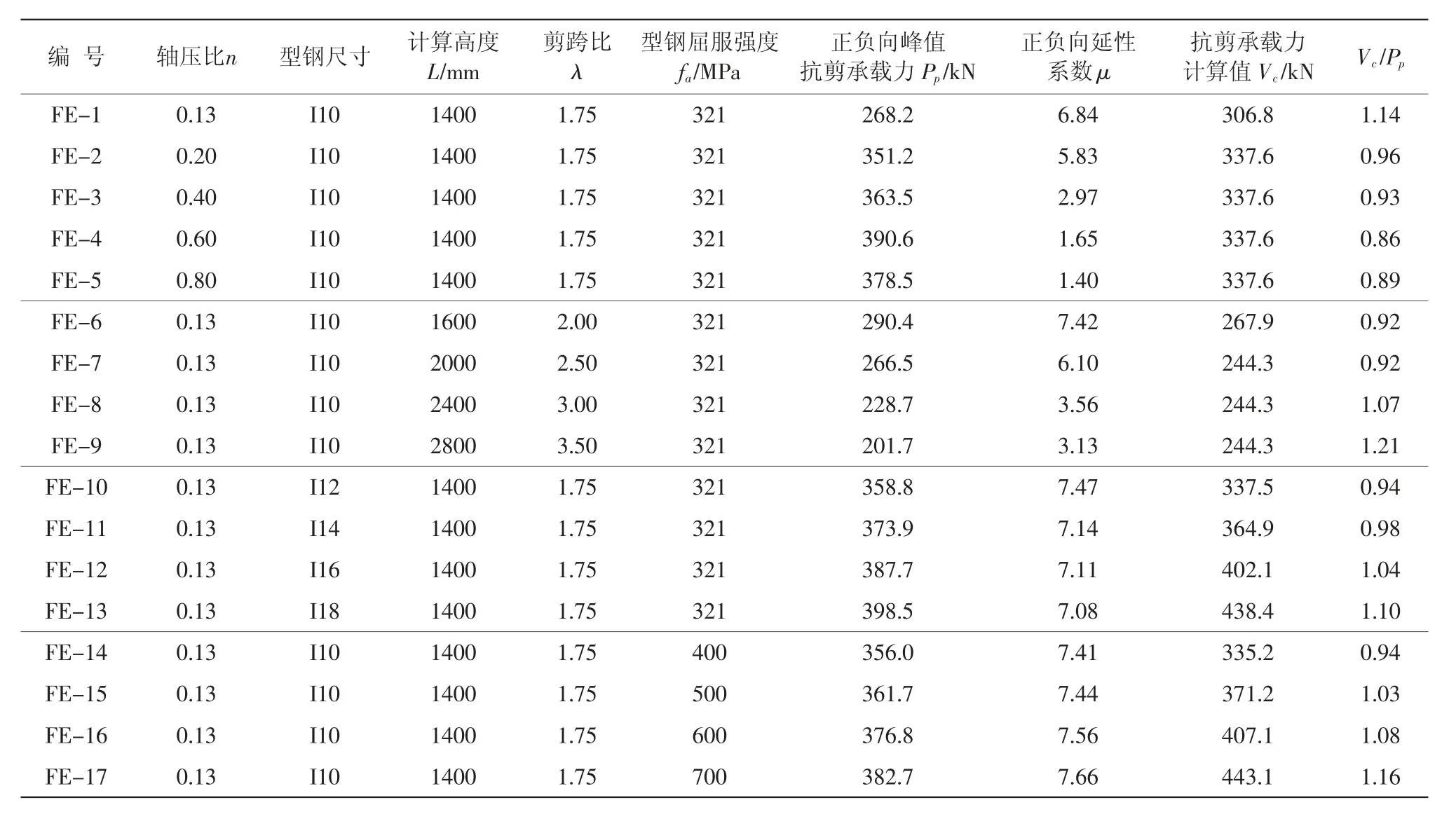
表2 拓展试件参数及计算结果

3.1 不同轴压比试件的骨架曲线（见图8）

由图8可见，随着轴压比的增大，试件的峰值承载力先增大后减小，且曲线有明显的凸起和陡降，呈现一定的延性退化。由表2可见，相较于轴压比n=0.13的试件FE-1，轴压比为0.20、0.40、0.60、0.80试件的峰值抗剪承载力分别提高了30.9%、35.5%、45.6%、41.1%。延性系数出现了大幅下降，在轴压比大于0.20时延性系数小于3。整体上看，轴压比的增大对X型支撑混凝土剪力墙的抗剪承载力有促进作用，但当轴压比大于0.2后提升效率约在10%以下，且延性退化明显，说明该组合剪力墙轴压比在0.2左右较为适宜。

3.2 不同剪跨比试件的骨架曲线（见图9）

由图9可见，随着剪跨比的增大，试件负向骨架曲线基本相似，而正向骨架曲线峰值点逐渐向右下方移动，初始斜率也逐渐降低，呈现一定弯曲破坏特征。由表2可见，随着剪跨比的增大，试件的峰值抗剪承载力和延性系数先提高后降低，相较于剪跨比为1.75的试件FE-1，剪跨比为2.00的试件峰值抗剪承载力和延性系数分别增大了8.2%、8.5%；而剪跨比为2.50、3.00、3.50的试件峰值抗剪承载力和延性系数分别降低了0.6%、14.7%、24.8%和10.8%、48.0%、54.2%。整体上看，剪跨比为2左右时试件的力学性能最佳，为X型支撑的最佳剪跨比。

3.3 不同型钢尺寸试件的骨架曲线（见图10）

由图10可见，不同型钢尺寸试件的骨架曲线形状相似，在达到峰值荷载后没有明显的下降段。由表2可见，随着型钢尺寸的增大，试件的峰值承载力逐渐增大，而延性系数先增大后减小。相较于内置型钢为I10的试件FE-1，内置型钢为I12、I14、I16、I18试件的峰值抗剪承载力分别提高了33.8%、39.4%、44.6%、48.6%，延性系数分别增大了9.2%、4.4%、3.9%、3.5%。这可能是因为型钢尺寸的增大虽然在一定程度上增大了强度和延性，但由于随着尺寸增大导致刚度增大，因此型钢与混凝土协同作用变差，不能同时达到极限强度，所以延性出现了降低，但整体上看降幅在10%内，并不明显。

3.4 不同型钢屈服强度试件的骨架曲线（见图11）

由图11可见，随着型钢屈服强度的提高，试件负向骨架曲线基本相似，值得注意的是当型钢屈服强度由321 MPa提高至400 MPa后，试件的骨架曲线在进入塑性段前基本重合，且随着型钢屈服强度的提高，二次刚度逐渐增大。由表2可见，相较于型钢屈服强度为321 MPa的试件，型钢屈服强度为400、500、600、700 MPa试件的峰值抗剪承载力分别提高了32.7%、34.9%、40.5%、42.7%，延性系数分别增大了8.3%、8.8%、10.5%、12.0%。整体上看，型钢屈服强度为400 MPa时提高最明显。

4 轴压比限值

从上述参数分析可知，轴压比及剪跨比是影响X型支撑剪力墙变形能力的主要原因。因此，有必要提出两者的匹配关系以保证其变形能力，依照JGJ 3—2010《高层建筑混凝土结构技术规程》对钢筋混凝土结构延性系数最低3.00为标准，经过近60个试件的试算（每种剪跨比进行轴压比0.1～0.3的试验，跨度0.01），最终的试验轴压比和设计轴压比与剪跨比匹配关系见表3。其中，考虑荷载组合系数和材料强度分项系数，试验轴压比与设计轴压比关系大致为：设计轴压比=1.625×试验轴压比。

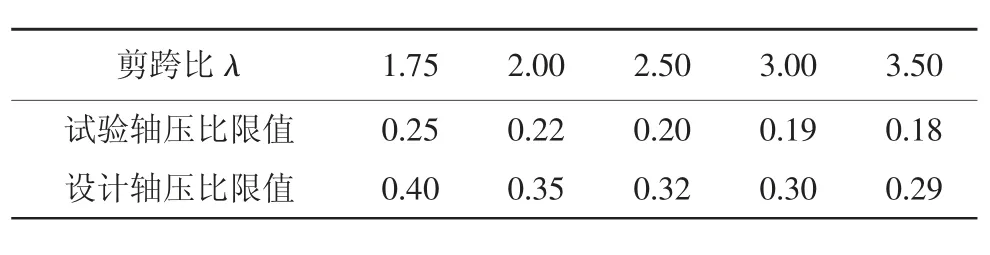
表3 轴压比限值

5 抗剪承载力计算方法

JGJ 3—2010规定，混凝土剪力墙受在偏心受压时的斜截面受剪承载力应符合：

型钢混凝土剪力墙的受剪承载力设计值计算公式参考JGJ 138—2016《组合结构设计规范》给出的无地震作用组合时计算公式为：

式中符号含义见JGJ 3—2010和JGJ 138—2016，式中第一、二、三项分别为混凝土、水平钢筋、型钢对抗剪承载力的贡献，第二项为水平钢筋对抗剪承载力的贡献。值得注意的是，α为型钢影响系数，对于垂直放置型钢的组合剪力墙，规范规定α=0.4。对于本文斜交叉放置的型钢，有必要进行修正。通过最小二乘法拟合得到斜交叉型钢支撑影响系数α=0.22，其抗剪承载力计算结果见表1。由表2可得，计算值与有限元结果比值为1.009，标准差为0.101，变异系数为0.102，所提出的X型支撑混凝土剪力墙抗剪承载力计算方法得到验证。