基于加速鲁棒特征图像匹配的云导风计算方法
2022-10-29孔德华宋志尧
孔德华, 张 东, 2, 张 卓, 宋志尧, 4
基于加速鲁棒特征图像匹配的云导风计算方法
孔德华1, 张 东1, 2, 张 卓2, 3, 宋志尧2, 3, 4
(1. 南京师范大学 海洋科学与工程学院, 江苏 南京 210023; 2. 江苏省地理信息资源开发与利用协同创新中心, 江苏 南京 210023; 3. 南京师范大学 虚拟地理环境教育部重点实验室, 江苏 南京 210023; 4. 大规模复杂系统数值模拟江苏省重点实验室, 江苏 南京 210023)
利用云导风技术结合高分辨率气象卫星遥感数据获取风矢量, 在监测台风等极端气象灾害方面具有重要应用。本文提出了一种基于加速鲁棒特征(speeded up robust features, SURF)图像匹配的云导风计算方法, 利用SURF算法结合随机抽样一致算法(random sample consensus, RANSAC), 提取并匹配两景连续时序云图的特征点, 计算风矢量, 并结合当地大气温度廓线指定云高, 经质量控制得到云导风矢量。运用该方法模拟了2018年台风“山竹”的云导风矢量, 以美国威斯康星大学气象卫星研究合作所(CIMSS)的大气运动矢量资料进行验证, 结果表明: (1) 风速和风向的相关系数分别为0.78和0.79, 均方根误差分别为4.75 m·s–1和37.64°, 平均绝对百分比误差分别为33.49%和22.55%, 整体具有良好的模拟精度; (2) 与CIMSS资料相比, 基于特征点匹配的SURF云导风计算方法在反演密集云区的风矢量有明显优势, 可有效提高云区内风矢量的数量, 扩大风矢量的空间覆盖范围; (3) 图像对比度增强处理对特征点的提取和风矢量的空间分布有重要影响, 伽马变换因子γ=5时, 能较好地平衡台风外围螺旋云带和中心附近云区的风矢量数量, 反映台风风场的整体特征。该方法作为基于尺度不变特征变换的云导风计算方法的改进, 可为利用卫星遥感影像数据进行云导风计算提供新的思路。
加速鲁棒特征算法; 图像匹配; 云导风; 风矢量; 台风
云导风技术是通过测算不同时相的气象卫星影像中云的运动来估计空间大范围风场的风速和风向的技术, 所得结果称为大气运动矢量或风矢量。风矢量资料广泛应用于风场数值模拟[1]、数值天气预报[2]等研究领域, 在台风、暴雨等各种气象灾害的监测、分析和预测上发挥着重要的作用[3-4]。
云导风技术最初是利用动画技术, 通过人工观测卫星云图中云的移动, 获得风场数据, 准确性较低[5]。20世纪70年代, Leese等[6]提出了相关系数法, 利用连续卫星云图间图像块的相似性, 基于模板匹配技术追踪示踪云图像块的运动, 得出风矢量。相关系数法作为云导风技术的重要算法沿用至今, 但其运算量较大, 运算效率较低[7]。在探索不同于模板匹配的云导风技术过程中, 王振会等[8]利用傅立叶相位分析法对示踪云进行频域波谱分析, 通过谐波的相位变化计算波速, 得到风矢量, 从而避免了相关系数法产生的“亚像元尺度位移”问题[9], 但是造成的相位重叠使得计算风速偏小[10]。马侠霖等[11]提出了基于尺度不变特征变换(scale invariant feature transform, SIFT)的云导风计算方法, 通过在连续两幅云图中追踪图像特征点的位置变化得到风矢量。该方法以像元而非图像块进行匹配, 克服了示踪云模板的制约, 因此不受云团形变的影响, 得到的风矢量精度较高。但在实际应用中发现, SIFT云导风方法得到的风矢量数量较少, 难以体现风场的整体特征。
风矢量数量由图像上匹配到的特征点对数量的多少决定, SIFT法造成风矢量较少的原因与图像特征点提取算法有关。在众多图像特征提取算法中, 由Hebert Bay等[12]提出的加速鲁棒特征算法(speeded up robust features, SURF)是对SIFT算法的改进, 在保证了尺度和旋转的鲁棒性的同时, 大大减少了算法的运算量, 被广泛应用于图像匹配[13]、配准[14]、跟踪[15]等方面, 取得了良好效果。因此, 本文拟从图像灰度特征出发, 运用SURF算法提取相邻时序台风影像的特征点, 结合特征点匹配方法与随机抽样一致算法(random sample consensus, RANSAC)实现风矢量的追踪, 并在此基础上构建完整的云导风计算方法, 探讨其在高时空分辨率气象卫星遥感影像中的风场提取能力, 为利用气象卫星遥感技术快速获取台风风场信息, 监测和预测台风运动, 减少极端气象灾害带来的危害提供方法和数据支撑。
1 基础数据
2018年第22号台风“山竹”于2018年9月7日在西北太平洋上生成, 11日晚发展为超强台风, 15日上午转为强台风, 16日17时登陆我国广东省江门市台山海宴镇, 登陆时中心附近最大风力14级(45 m·s–1), 是2018年登陆我国的最强台风[16]。本文以台风“山竹”为例, 收集了以下三类数据, 实现基于云导风方法的风矢量计算试验: 1) 高分辨率气象卫星影像数据; 2) 大气温度垂直廓线数据; 3) 风矢量精度验证数据。
1.1 卫星影像数据
葵花-8号(Himawari-8)气象卫星是日本气象厅在2014年10月发射的新一代地球同步静止气象卫星[17], 全盘扫描观测时间间隔10 min, 影像空间分辨率0.5~2 km, 共有16个观测波段, B13红外波段(波长10.4 µm)、B3可见光波段(波长0.64 µm)、B9水汽波段(波长7.0 µm)被用于业务化的云导风矢量计算[18]。红外波段具有全天时、全天候成像能力, 同时也是追踪云层运动的有效波段[19]。因此, 本文选用Himawari-8气象卫星B13红外波段的亮温影像转换得到的灰度影像来进行风矢量的反演。针对2018年第22号台风“山竹”的登陆过程, 选取了北京时间2018年9月15日8时、14时和20时; 9月16日2时、8时和14时的6个整点时刻及各个整点的后10 min时刻共计12个时刻的卫星影像, 按整点时刻分为6组, 每组包含前后间隔10 min的两幅影像。所有影像经过辐射定标、几何校正后, 裁剪出台风“山竹”所在区域, 用于模拟台风登陆前后的云导风风场。
1.2 大气温度垂直廓线数据
大气温度垂直廓线数据来自美国国家环境预报中心(NCEP)网站(https: //rda.ucar.edu)的全球再分析资料, 该资料包括地表温度和大气温度廓线, 大气垂直廓线分为26个高度层, 分别对应1000、975、950、925、900、850、800、750、700、650、600、550、500、450、400、350、300、250、200、150、100、70、50、30、20和10 hpa气压高度[20], 空间分辨率为1°×1°。本文选取覆盖了台风影像区域的六个整点时刻的全球再分析资料, 从中获得大气温度垂直廓线数据, 用于风矢量的高度指定。
1.3 风矢量验证数据
用于对比和验证的云导风资料来自美国威斯康星大学气象卫星研究合作所(CIMSS)网站(http:// tropic.ssec.wisc.edu)的大气运动矢量(Atmospheric Motion Vectors, AMVs)数据集。该资料包含有风矢量的经纬度、风速、风向、气压高度等信息。搜集了与实验结果相对应的6个整点时刻的红外波段大气运动矢量资料, 用于验证和评价本实验得到的风矢量精度。
2 研究方法
本文提出基于SURF算法的云导风计算方法, 将图像增强和特征点匹配技术相结合, 运用在时序卫星云图上, 通过红外波段云图反演出风矢量, 具体技术路线如图1所示。技术流程图中的关键技术方法概要介绍如下。实验中使用的SURF算法、匹配算法以及RANSAC算法通过Python语言调用OpenCV开源库中的相应方法实现。
2.1 图像增强
对比度强、细节特征明显的图像有利于特征点提取。从收集到的Himawari-8卫星红外波段影像可以看出(图2a), 影像中云区像元的灰度值较高, 无云区像元的灰度值较低。特别是对于台风区域, 云区的覆盖范围大且密集, 云区像元的灰度值接近, 使得图像整体偏亮且对比度不高。为提高图像对比度, 突出云区细节特征, 采用伽马变换对图像进行增强处理。伽马变换是对输入灰度值in进行的非线性操作, 变换公式如下:

式中, 输入灰度值Iin归一化至[0, 1]区间; c为灰度缩放系数, 本文取c=255, 使输出灰度值Iout的取值范围在0~255之间。γ为伽马因子, 当γ<1时, 图像整体变亮; 反之图像整体变暗。经试验, 取γ=5可取得好的图像增强效果, 具体对比如图2a、2b所示。可以看到, 经伽马变换后, 台风外围云区中的图像细节被压抑, 而密集云区中的图像对比度增加, 细节得到增强。
a. 台风云图; b. 图像增强后的台风云图
2.2 特征点提取
根据特征点在两幅相邻时刻台风云图中的位置变化, 可以计算得到其所在像元上的风矢量, 因此特征点提取算法对最终的云导风计算结果至关重要。SURF算法[21]基于不同尺度下的近似Hessian矩阵检测图像特征点, 尺度空间分成4组, 每组包含4层图像。图中某点(,)的近似Hessian矩阵surf定义为:


式中,D,D,D分别是高斯滤波模板简化后得到的盒子滤波器与积分图像函数在该点处的卷积;为尺度因子,为以像元个数计数的盒子滤波器的边长。由此可得近似Hessian矩阵的行列式如下:
det(surf) = DD– (0.9D)2, (4)
对尺度空间中的每层图像计算近似Hessian行列式得到局部极值点, 以相邻三层图像的中间层的每个局部极值点为中心, 在当前层和上、下层中分别选取该点周围3×3邻域内的像元, 构成3×3×3的立体邻域。若该极值大于立体邻域其他26个像元的近似Hessian行列式值, 则确定该局部极值点为特征点。
得到图像特征点后需要确定特征点的主方向和特征向量, 作为特征点匹配时的依据。以特征点为圆心, 对半径为6的圆形区域内的像素进行Haar小波变换, Haar小波滤波器模板如图3所示, 模板边长为4, 其中黑色区域权重为–1, 白色区域权重为1。统计所有特征点在和方向上的Haar小波响应值, 以60°的扇形窗口遍历整个圆形区域, 计算窗口内的特征点的Harr小波响应值相加形成的局部方向向量, 最长向量方向则为该特征点主方向。如图4所示, 红色箭头方向即为该特征点的主方向。
注: a. Haar小波在方向上的滤波器模板; b. Haar小波在方向上的滤波器模板
特征向量的计算过程如图5所示, 以每个特征点为中心, 构建边长为20的正方形窗口, 并旋转到特征点的主方向(图5中红色箭头方向), 将其分为16个边长为5的正方形子区域, 计算每个子区域的像元在水平方向和垂直方向上的Haar小波响应值之和Σd、Σd及其绝对值之和Σ|d|与Σ|d|, 得到一个4维特征向量= {Σd, Σd, Σ|d|, Σ|d|}, 串接16子区域的特征向量, 得到该特征点的64维特征向量。
2.3 特征点匹配
分别提取出两幅时序云图中的所有特征点后, 基于特征向量的相似度, 对前一时刻影像的每个特征点, 在后一时刻找到与之最相似的特征点进行匹配。选择欧氏距离Dis作为特征向量相似度的评判依据, 欧氏距离最小时认定两点的特征向量最相似, 两个特征点相互匹配。Dis计算公式如下:

式中,V表示前一时刻影像中第个特征点对应的特征向量的第个元素;V表示后一时刻影像中第个特征点对应的特征向量的第个元素。
2.4 误匹配过滤
利用欧氏距离进行特征点匹配的过程中, 会存在少量特征向量最相似的特征点对并非合理匹配的情况。为提高特征点匹配的准确度, 减少后续风矢量计算时出现异常值的概率, 本文采用RANSAC算法来减少特征点误匹配情况[22]。RANSAC算法的具体步骤如下:
1) 从全部组匹配点对中随机提取4组匹配点对, 求解对应的单应性变换矩阵, 其表达式为:
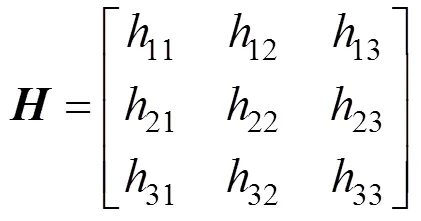


2) 根据该变换矩阵, 对前一时刻特征点集中的其余-4个特征点进行变换, 计算变换后的每个点的坐标与原匹配点的坐标之间的距离。若距离小于阈值, 则认为该特征点为此变换下的内点, 否则为外点, 记录内点数量, 阈值设定为5个像元的长度。
3) 重复1-2步骤若干次, 内点数量最多时的变换矩阵′即为正确的变换矩阵。
4) 将正确的变换矩阵下的内点保留, 外点去除, 实现对特征匹配结果的优化, 完成特征点误匹配过滤。
2.5 风矢量高度指定
得到正确匹配的特征点对结果后, 根据已知时间间隔内每组匹配点对中的两个特征点间的位置变化, 计算出风矢量的大小和方向, 得到初始风矢量。由于风矢量在云顶高度附近, 因此推算云高即可得出风矢量的高度估计值。云顶高度通过结合大气温度垂直廓线数据和红外云图云顶亮温值来推算[23], 其中大气温度垂直廓线中的温度采用经转换后的亮度温度。设风矢量所在位置的云顶亮温值为(K), 对应的气压高度为(hpa), 风矢量高度计算的步骤如下:
1) 根据风矢量的坐标, 在大气温度垂直廓线数据中提取该位置的26个高度层对应的大气温度集合emp = {1,2,3, …,26}, 其中1>2>3>…>26。
2) 对于风矢量所在像元的云顶亮温值, 若能在集合emp中找到与相等的亮温值, 则直接查得所对应的气压高度值;
3) 若不能在集合emp中直接找到与相等的亮温值, 则通过对数线性插值法计算对应的气压高度。对数线性插值公式如下:

式中,1、2分别为亮温值1、2对应的大气温度垂直廓线高度层的气压高度。1、2的取值分三种情况: 若>1, 则令1=2,2=1; 若<26, 则令1=26,2=25; 若26<<1, 则将集合中与最相近的两个亮温值分别记为1、2, 且2<<1。
2.6 风矢量质量控制
为确保每个风矢量与周围风矢量的属性差异在合理范围内, 分别通过计算每个风矢量与其邻域内风矢量的风速均方根误差和风向均方根误差, 设置阈值剔除误差较大的风矢量, 实现对初始风矢量的质量控制[10]。Holmlund认为在进行风矢量质量控制时, 以目标矢量为中心的正方形邻域的边长应设定为100~200 km[24]。由于实验采用影像的空间分辨率为4 km, 故设定目标风矢量正方形邻域搜索范围的边长为50个像元。Endlic和McLean发现对于高空急流, 在1°的纬度范围内, 风速的衰减约为15%, 且气流越强风速的衰减越大[25], 因此风速均方根误差的阈值设定为正方形邻域内最大风速的40%。风向均方根误差的阈值参考马侠霖等的取值, 设定为100°[10]。风速均方根误差R和风向均方根误差R的计算公式如下:


式中,、为目标风矢量的风速和风向;v、d为邻域风矢量的风速和风向;为邻域内除目标风矢量以外的风矢量个数。
3 结果
3.1 台风“山竹”的云导风矢量结果
利用收集到的台风“山竹”12个时刻的Himawari-8卫星遥感影像数据, 采用SURF云导风方法计算得到6个整点时刻的风矢量结果如图6所示。对于这6个时刻台风“山竹”的云导风矢量结果, 从风速分布来看, 北部云区的风速普遍大于南部云区, 风速超过30 m·s–1的风矢量集中分布在台风中心附近以北的云区, 且最大风速均小于40 m·s–1。由这些区域向外, 风速逐渐减小, 风速小于5 m·s–1的风矢量集中分布在南部的外围螺旋云系。从风速变化来看, 图6(a)~(c)中, “山竹”西南侧云系的风速增大, 增强的气流为中心云系输送了能量, 风眼逐渐出现, 台风强度有增强趋势, 眼区附近风速逐渐增大; 图6(d)中台风眼最为清晰, 围绕眼区分布的风矢量的最为密集; 图6(e)~(f)中风速较大的风矢量分散到外围云区, 风眼逐渐消散, 来自东南侧的急流云系维持着向中心云区的能量输送。计算得到的风矢量主要分布在400 hpa气压高度以上, 150 hpa气压高度以下, 图7所示为3个整点时刻中气压高度在150~200 hpa之间的风矢量。可以看出, 红外波段台风影像中, 亮白云团的高度较高, 台风中心附近的亮白云团呈顺时针向外辐散的运动趋势。总体上, SURF云导风方法计算得到的风矢量能有效显示台风发展变化过程中云团运动速度的变化情况。
3.2 风矢量精度验证
由于探空测站主要位于陆地, 难以获取台风在海上阶段的实测风速数据, 因此采用CIMSS的大气运动矢量数据集来对SURF云导风方法反演的风矢量进行精度验证。由于得到的风矢量具有不同的高度, 因此精度验证时, 以本方法所得风矢量为基准, 在数据集中选择垂直方向气压高度相差100 hpa以内、水平方向经纬度相距0.1°范围内的最邻近的矢量, 采用平均绝对误差(Mean Absolute Error, MAE)、平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)、均方根误差(Root Mean Square Error, RMSE)和相关系数()四个指标分别从风速和风向两方面对风矢量的精度进行验证, 结果如表1所示。六个时刻的风速和风向平均相关系数分别为0.78和0.79, 均方根误差分别为4.75 m·s–1和37.64°, 平均绝对百分比误差分别为33.49%和22.55%。风速与风向的绝对值误差分布如图8所示。风速绝对值误差小于6 m·s–1的风矢量占总数量的82.6%, 风向绝对值误差小于40°的风矢量占总数量的83.7%, 可见本方法所得风矢量的风速、风向与CIMSS大气运动矢量资料吻合良好。
注: a. 9月15日08时; b. 9月15日14时; c. 9月15日20时; d. 9月16日02时; e. 9月16日08时; f. 9月16日14时
注: a. 9月15日14时; b. 9月15日20时; c. 9月16日02时

表1 SURF云导风方法风矢量精度验证
注: a. 风速差绝对值; b. 风向差绝对值
3.3 风矢量空间分布对比
图9显示了SURF云导风方法风矢量与CIMSS风矢量在所有高度上的空间分布对比。可以看出, SURF云导风方法所得风矢量与CIMSS资料风矢量在空间上具有不同的分布特征。从Himawari-8卫星红外波段台风影像上看, 在台风外围区域, 云层较薄, 像元灰度值小, 图像细节特征较少, 不利于特征点的提取和匹配, 因此基于图像特征点追踪的SURF云导风方法得到的风矢量明显少于CIMSS资料风矢量。而在台风云区, 由于台风气旋的螺旋型形态, 导致不同云高的像元灰度值之间存在差异, 图像对比度增大, 细节特征增强, 因此在有CIMSS风矢量的区域, SURF云导风方法基本上均能反演得到风矢量, 而在台风眼下方区域, SURF云导风方法反演的风矢量明显多于CIMSS数据集在该区域的风矢量。虽然这部分风矢量缺少实测数据可以直接验证其精度, 但是定性来看, 风矢量的风速大小与周围的风矢量相近, 风矢量的方向也呈现明显的逆时针螺旋型分布趋势, 因此可以认为其能够代表当前的台风风场。可见相比于CIMSS风矢量资料, SURF云导风方法在反演密集云区的风矢量时具有较大优势。
4 讨论
4.1 伽马因子对特征点提取结果的影响
由于SURF算法基于图像尺度空间的极值计算特征点, 图像增强处理的结果直接影响图像特征点的提取, 进而影响风矢量的计算结果以及空间分布。为探究图像增强处理时伽马因子的取值对后续图像特征点计算的影响, 以确定合适的值, 分别对各个时刻影像取= 1, 2, 3, …, 12进行伽马变换和基于SURF的特征点提取。由于台风“山竹”云系庞大, 直径范围达1 000 km, 因此以台风中心为圆心、500 km半径确定圆形区域, 将台风“山竹”的云图分为内外两个云区, 内云区位于圆形区域内, 包含台风眼区、云墙区和部分螺旋云带; 外云区位于圆形区域外, 主要为外围螺旋云带。图10显示了不同γ取值下内、外云区中的特征点数量对比。
可以看出, 伽马因子的取值大于1时, 随的增大, 外云区的特征点数量不断减少, 而内云区的特征点数量则波动增加, 达到最大值后出现逐渐减少的趋势。在多数时刻下, 大致在=5时内云区的特征点数量会出现一个峰值。若继续增大, 内云区特征点的数量不再增加或增幅较小, 而外云区特征点的数量则持续减少。因此, 若从选取单一值的角度, 取=5, 可以有效突出内云区台风眼和云墙区的风矢量, 同时较好地维持台风风场总的风矢量数量, 体现整体台风云区的螺旋形风场特征。
4.2 特征点提取方法对云导风结果的影响
为研究特征点提取方法对云导风结果的影响, 以SIFT云导风方法对台风“山竹”进行了风矢量反演, 除了特征点提取方法不同以外, 其余数据处理步骤都与SURF云导风方法一致。同样以CIMSS大气运动矢量资料对风矢量反演结果进行验证, 结果如表2所示。SIFT云导风方法得到的风矢量的风速和风向平均相关系数分别为0.81和0.85, 均方根误差分别为4.11 m·s–1和31.22°, 平均绝对百分比误差分别为25.25%和21.75%。与SURF云导风方法相比, 两种方法的误差比较接近, 总体上SIFT云导风方法得到的风矢量的精度上略高。

表2 SIFT云导风方法风矢量精度验证
图11显示了基于SURF算法和SIFT算法得到的风矢量反演结果的空间分布对比。可以看到, SURF方法得到的风矢量数量明显多于SIFT方法的结果。SIFT云导风方法得到的风矢量集中分布在云区边缘和台风中心附近区域, 而SURF云导风方法得到的风矢量在台风云区有更广泛的分布, 特别是在台风眼附近及下方区域, 因此台风风场的螺旋形形态特征也更明显。造成这种差异的原因是SURF算法在图像尺度空间构造、特征点检测的过程、特征向量方向的确定和特征描述符的生成四个方面优化和改进了SIFT算法, 在图像的更多位置提取到了特征点, 最终得到了更多风矢量。不同时刻下两种方法得到的台风“山竹”的风矢量数量对比如表3所示, 基于SURF的云导风方法得到的风矢量在数量上平均增加了49.6 %。因此, 在台风风矢量模拟精度相近的情况下, SURF云导风方法比SIFT云导风方法对台风风场有更好的代表性, 也能更好地描述台风风场的空间形态。
5 结论
本文提出了一种基于快速鲁棒特征(SURF)图像匹配的云导风计算方法, 在运用伽马变换增强云区图像对比度的基础上, 利用SURF算法计算两景相邻时相台风红外波段影像的特征点, 以欧氏距离最小的原则完成相似特征点的匹配; 进一步引入RANSAC算法去除误匹配点对, 根据每组匹配中两点之间的位移计算出风速的大小和方向, 结合当地大气温度廓线指定云高, 经质量控制后得到最终的风矢量。以台风“山竹”为试验, 得出的研究结果表明:
(1) 以CIMSS数据集风矢量为验证, SURF云导风计算方法得到的风矢量的风速和风向的相关系数分别为0.78和0.79, 均方根误差分别为4.75 m·s–1和37.64°, 平均绝对百分比误差分别为33.49%和22.55%, 具有良好的模拟精度, 可有效用于台风风场的模拟, 为极端气象灾害的风场数值模拟提供参考数据。
(2) 对比CIMSS数据集的风矢量空间分布, SURF云导风计算方法在反演密集云区的风矢量时, 可以利用密集云区的特征点匹配, 得到更多的风矢量。因此该方法可以弥补基于模板匹配的云导风方法由于云团形变原因等无法找到合适的示踪云块, 从而无法得到密集云区的风矢量的缺陷, 进一步扩大云区内风矢量的空间覆盖范围。
(3) 对比基于尺度不变特征变换(SIFT)的云导风计算方法, 基于快速鲁棒特征(SURF)的云导风计算方法得到的风矢量的风速和风向模拟精度相近, 但是风矢量的数量平均增加49.6%, 显著扩大了风矢量的空间分布, 能够更好地描述台风风场的空间形态。
(4) 图像增强处理对特征点的提取数量具有重要影响。当伽马因子≥1时,取值较小对于反演台风外围螺旋云带的风矢量较为有利;取值较大适用于反演台风中心附近云区的风矢量。从选取单一值的角度, 发现当=5时, 能够适中平衡台风外围螺旋云带和台风中心附近云区的风矢量数量, 突出SURF云导风计算方法在反演内云区风矢量时的优势, 同时兼顾外云区风矢量, 较好地反映台风风场的整体特征。此外, 若针对内云区和外云区采用不同的, 风矢量的数量可能进一步增加, 从这一角度出发,的选取值得进一步研究。
致谢: 感谢河海大学海洋学院葵花卫星地面接收站提供的4 km分辨率的台风“山竹”Himawari-8气象卫星红外波段影像数据; 感谢美国国家环境预报中心(NCEP)提供的全球再分析资料和美国威斯康星大学气象卫星研究合作所(CIMSS)的大气运动矢量数据。
[1] 何斌, 翟国庆, 高坤, 等. 云迹风资料同化对东亚海域风场数值模拟的影响[J]. 海洋学报(中文版), 2007, 29(6): 23-32.
HE Bin, ZHAI Guoqing, GAO Kun, et al. The impact of cloud motion wind data on numerical simulation of wind field in the sea area of Eastern Asia[J]. Acta Oceanologica Sinica, 2007, 29(6): 23-32.
[2] 李华宏, 王曼, 薛纪善, 等. FY-2C云迹风资料在中尺度数值模式中的应用研究[J]. 气象学报, 2008, 66(1): 50-58.
LI Huahong, WANG Man, XUE Jishan, et al. A study on the application of FY-2C cloud drift wind in a mesoscale numerical model[J]. Acta Meteorologica Sinica, 2008, 66(1): 50-58.
[3] 刘瑞, 翟国庆, 王彰贵, 等. FY-2C云迹风资料同化应用对台风预报的影响试验研究[J]. 大气科学, 2012, 36(2): 350-360.
LIU Rui, ZHAI Guoqing, WANG Zhanggui, et al. Impact of application of cloud motion wind data from FY-2C satellite on simulation of typhoon cases[J]. Chinese Journal of Atmospheric Sciences, 2012, 36(2): 350-360.
[4] 周兵, 徐海明, 吴国雄, 等. 云迹风资料同化对暴雨预报影响的数值模拟[J]. 气象学报, 2002, 60(3): 309-317.
ZHOU Bing, XU Haiming, WU Guoxiong, et al. Numerical simulation of CMWDA with it’s impacting on torrential rain forecast[J]. Acta Meteorologica Sinica, 2002, 60(3): 309-317.
[5] IZAWA T, FUJITA T. Relationship between observed winds and cloud velocities determined from pictures obtained by the ESSA III, ESSA V and ATS-I satellites[J]. Space Research IX, Amsterdam, North-Holland Publ. Co, 1969: 571-579.
[6] LEESE J A, NOVAK C S, CLARK B B. An automated technique for obtaining cloud motion from geosynchronous satellite data using cross correlation[J]. Journal of Applied Meteorology and Climatology, 1971, 10(1): 118-132.
[7] 许健民, 张其松. 卫星风推导和应用综述[J]. 应用气象学报, 2006, 17(5): 574-582.
XU Jianmin, ZHANG Qisong. Status review on atmospheric motion vectors-derivation and application[J]. Journal of Applied Meteorological Science, 2006, 17(5): 574-582.
[8] 王振会, 许建明, G.KELLY. 基于傅立叶相位分析的卫星云图导风技术[J]. 气象科学, 2004, 24(1): 9-15.
WANG Zhenhui, XU Jianming, G.KELLY. Deriving cloud motion vectors from high temporal resolution images based on Fourier phase analysis technique[J]. Journal of the Meteorological Sciences, 2006, 17(5): 574-582.
[9] PURDOM J F. W. Detailed cloud motions from satellite imagery taken at thirty second, one and three minute intervals[C]//Proceeding to the 3rd international wind workshop in Ascona, Switzerland. 1996: 10-12.
[10] 许建明, 王振会. 傅立叶相位分析导风技术的适用范围和相位重叠分析[J]. 气象科学, 2004, 24(3): 309-313.
XU Jianming, WANG Zhenhui. The application condition of Fourier analysis technique and the analysis of phrase overlap[J]. Journal of the Meteorological Sciences, 2004, 24(3): 309-313.
[11] 马侠霖, 罗鹏, 陈志斌, 等. 基于尺度不变特征变换的云导风计算方法[J]. 气象科技, 2014, 42(3): 391-396.
MA Xialin, LUO Peng, CHEN Zhibin, et al. A method for cloud motion wind vector prediction based on Scale- Invariant Feature Transform[J]. Meteorological Science and Technology, 2014, 42(3): 391-396.
[12] BAY H, TUYTELAARS T, VAN GOOL L. Surf: Speeded up robust features[C]//European conference on computer vision. Springer, Berlin, Heidelberg, 2006: 404-417.
[13] 黄春凤, 刘守山, 别治峰, 等. 改进的SURF算法在图像匹配中的应用[J]. 现代电子技术, 2020, 43(10): 111-115.
HUANG Chunfeng, LIU Shoushan, BIE Zhifeng, et al. Application of improved SURF algorithm in image matching[J]. Modern Electronics Technique, 2020, 43(10): 111-115.
[14] 唐颖复, 王忠静, 张子雄. 基于改进SIFT和SURF算法的沙丘图像配准[J]. 清华大学学报(自然科学版), 2021, 61(2): 161-169.
TANG Yingfu, WANG Zhongjing, ZHANG Zixiong. Registration of sand dune images using an improved SIFT and SURF algorithm[J]. Journal of Tsinghua University (Science and Technology), 2021, 61(2): 161-169.
[15] 权巍, 包铁壮, 白宝兴, 等. SURF与RANSAC算法结合的图像跟踪方法[J]. 计算机仿真, 2016, 33(9): 268-272.
QUAN Wei, BAO Tiezhuang, BAI Baoxing, et al. A method of real-time picture tracking and mapping based on SURF algorithm and RANSAC algorithm[J]. Computer Simulation, 2016, 33(9): 268-272.
[16] 方艳莹, 钱燕珍, 申华羽, 等. 1822号台风“山竹”引起浙江东北部大暴雨成因分析[J]. 海洋预报, 2020, 37(4): 86-96.
FANG Yanying, QIAN Yanzhen, SHEN Huayu, et al. Causes analysis on the heavy rainfall in northeastern Zhejiang related to the typhoon “Mangkhut” (1822)[J]. Marine Forecasts, 2020, 37(4): 86-96.
[17] 周旋, 叶小敏, 周江涛, 等. 基于Himawari-8卫星的逐时次海表温度融合[J]. 海洋学报, 2021, 43(1): 137-146.
ZHOU Xuan, YE Xiaomin, ZHOU Jiangtao, et al. Hourly sea surface temperature fusion based on Himawari-8 satellite[J]. Acta Oceanologica Sinica, 2021, 43(1): 137- 146.
[18] SHIMOJI K. Introduction to the Himawari-8 atmospheric motion vector algorithm[J]. Meteorological Satellite Center Technical Note, 2017, 62: 73-77.
[19] OYAMA R, SAWADA M, SHIMOJI K. Diagnosis of tropical cyclone intensity and structure using upper tropospheric Atmospheric Motion Vectors[J]. Journal of the Meteorological Society of Japan. Ser. II, 2018, 96: 3-26.
[20] 王静, 赵朝方. 最小方差算法反演NOAA/AMSU海面大气温度垂直廓线[J]. 海洋湖沼通报, 2008(2): 16-23.
WANG Jing, ZHAO Chaofang. Retrieval of atmospheric vertical temperature profile over sea from NOAA/AMSU data with minimum variance algorithm[J]. Transactions of Oceanology and Limnology, 2008(2): 16-23.
[21] BAY H, ESS A, TUYTELAARS T, et al. Speeded-up robust features (SURF)[J]. Computer vision and image understanding, 2008, 110(3): 346-359.
[22] FISCHLER M A, BOLLES R C. Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography [J]. Communications of the ACM, 1981, 24(6): 381-395.
[23] 许建明. 一维傅立叶相位导风技术的研究[D]. 南京: 南京气象学院, 2003.
XU Jianming. Research on one-dimensional Fourier phase wind guide technology[D]. Nanjing: Nanjing meteorological College, 2003.
[24] HOLMLUND K. The utilization of statistical properties of satellite-derived atmospheric motion vectors to derive quality indicators [J]. Weather and Forecasting, 1998, 13(4): 1093-1104.
[25] ENDLICH R M, MCLEAN G S. The structure of the jet stream core [J]. Journal of Atmospheric Sciences, 1957, 14(6): 543-552.
A cloud-motion-based wind retrieval method based on the SURF algorithm
KONG De-hua1, ZHANG Dong1, 2, ZHANG Zhuo2, 3, SONG Zhi-yao2, 3, 4
(1. College of Marine Science and Engineering, Nanjing Normal University, Nanjing 210023, China; 2. Jiangsu Center for Collaborative Innovation in Geographical Information Resource Development and Application, Nanjing 210023, China; 3. Key Lab of Virtual Geographic Environment under the Ministry of Education, Nanjing Normal University, Nanjing 210023, China; 4. Jiangsu Provincial Key Laboratory for Numerical Simulation of Large Scale Complex System, Nanjing 210023, China)
Cloud-motion-based wind retrieval technology combined with high-resolution meteorological satellite remote sensing data to obtain wind vectors has crucial applications in monitoring extreme meteorological disasters such as typhoons. In this study, a cloud-motion-based wind retrieval method based on the speeded-up robust features (SURF) image matching algorithm is proposed. The SURF and random sample consensus algorithms are used to extract and match the feature points of two consecutive time-series cloud images, calculate the wind vectors, and specify cloud height in combination with the local atmospheric temperature profile. The cloud-motion-based wind retrieval vectors are obtained through quality control. The proposed method is used to simulate the cloud- motion-based wind retrieval vectors of Typhoon “Mangkhut” in 2018, which is verified using the Cooperative Institute for Meteorological Satellite Studies (CIMSS) atmospheric motion vector data. The results indicate that: (1) The correlation coefficients of wind speed and wind direction are 0.78 and 0.79, respectively, the root mean square errors are 4.75 m·s−1and 37.64°, respectively, and the average absolute percentage errors are 33.49% and 22.55%, respectively, which has good simulation accuracy overall. (2) Compared with the CIMSS data, the cloud-motion- based wind retrieval method based on the SURF feature matching algorithm has obvious advantages in retrieving wind vectors in dense cloud areas, which can effectively improve the number of wind vectors in cloud areas and expand the spatial coverage of wind vectors. (3) Image contrast enhancement highly impacts the extraction of feature points and the spatial distribution of wind vector= 5, which can better balance the number of wind vectors in the spiral cloud belt and the area near the center of the typhoon, reflecting the overall characteristics of the typhoon wind field. As an improvement of the cloud-motion-based wind retrieval method based on scale- invariant feature transformation, the proposed method can be a new approach for wind vector calculation using satellite remote sensing image data.
SURF algorithm; image matching; cloud-motion-based wind retrieval; wind vectors; typhoon
Nov. 13, 2021
TP751
A
1000-3096(2022)09-0064-13
10.11759/hykx20211113001
2021-11-13;
2022-03-12
国家重点研发计划项目(2018YFB0505500, 2018YFB0505502)
[National Key R & D Program of China, Nos. 2018YFB0505500, 2018YFB0505502]
孔德华(1996—), 男, 江苏南京人, 硕士研究生, 主要从事风矢量遥感反演研究, E-mail: 1290304214@qq.com; 张东(1975—), 男,通信作者, 江苏南通人, 博士, 副教授, 研究方向为海洋信息技术与海岸带资源开发管理, E-mail: zhangdong@njnu.edu.cn
(本文编辑: 康亦兼)
