高压涡轮叶片缘板阻尼片阻尼效果试验研究

杜传宇，姜 睿，刘跃聪，杨洪旭

(中国航发沈阳发动机研究所，沈阳 110015)

1 引言

航空发动机涡轮转子叶片是将高温燃气内能转化成机械能的关键部件。叶片长期在高温、高压、高转速的环境中工作，不仅要承受热应力和离心力，还要承受复杂气动载荷的作用；当气流激励频率与叶片固有频率一致时还会发生较大应力的共振。在这种环境下长时间试车后，叶片时常发生高周疲劳断裂故障。为避免此类故障发生，李其汉等[1]提出采取各种阻尼减振措施，以减小、抑制叶片动力响应，达到降低叶片高周疲劳失效风险的目的。其中，在叶身增加干摩擦阻尼结构作为一种有效的减振方式，已得到广泛应用[2]。

叶片干摩擦阻尼结构发展至今，主要有凸肩结构、叶冠结构和缘板阻尼结构等[3]。凸肩结构主要用于风扇叶片及压气机前几级叶片[4]；叶冠结构常用于低压涡轮转子叶片。针对高压涡轮转子叶片通常采用缘板阻尼结构进行减振，而缘板阻尼结构包含多种不同结构形式。吴向宇等[5]查阅国内外发动机型号的缘板阻尼结构，总结出了几种典型的结构形式：薄片式(CFM56-3)、棱柱式(CFM56-5/7)、异型结构(盒状、弹簧状等)。

目前针对缘板阻尼结构减振特性的理论分析和计算分析取得了多项研究成果[6-11]，但多数分析存在以下两个问题：①叶片结构的简化和分析模型的选择，很难找到一个通用的摩擦模型和接触面运动模型解释所有的摩擦现象[12]。②难以解析干摩擦过程中存在的强非线性。为此，需借助试验研究来分析和优化缘板阻尼结构。Griffin 等[13-14]做了B-G 型缘板阻尼器的分析以及试验验证；郝燕平等[15]对带缘板阻尼片的金属平板模拟件做了试验研究，给出了叶片-叶片模型阻尼片减振规律。但在多个试验研究中，对于实际工作中缘板两侧安装阻尼片的三联装真实涡轮叶片的试验分析相对较少。本文针对某型带缘板阻尼片结构高压涡轮叶片的断裂故障，采用真实高压涡轮工作叶片进行试验，通过测量模态阻尼和叶片根部一弯最大应力点的应变响应曲线，研究缘板阻尼片在不同压紧力下的阻尼效果。

2 试验系统搭建

发动机实际工作中，阻尼片结构搭接在相邻叶片的缘板下方，在叶片振动时提供摩擦阻尼以降低其振动应力。为模拟真实阻尼状态，即在1 片叶片的缘板两侧均有阻尼结构，试验采用3 片真实发动机高压涡轮叶片联装形式，中间1片叶片为待测件，上、下2 片将叶片截去，以降低叶片间的耦合作用，同时方便测试。阻尼片为模拟件，材料为45 号钢，结构见图1。

图1 阻尼片模拟件Fig.1 Simulator of damper

阻尼片与缘板间正压力的施加方式为顶紧式。利用4：1 力臂的杠杆结构施加顶紧力，杠杆一端用砝码加载，另一端通过顶杆顶住阻尼片，加载示意图见图2(图中虚线为另一阻尼片加载方式)。

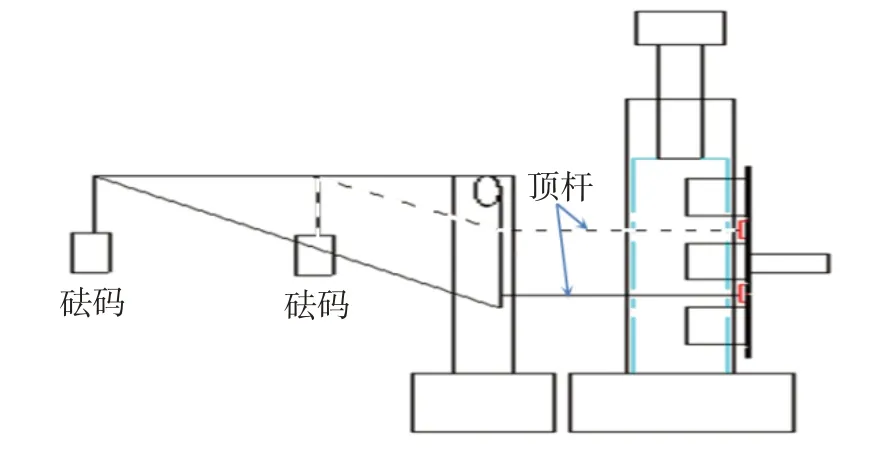
图2 加载示意图Fig.2 Schematic diagram of loading

模态试验时，将带有叶片的试验装置通过夹具固定在台面上，并用螺栓压紧叶片。在叶身布置敲击点，如图3所示。试验时固定加速度传感器位置，通过移动力锤测量每个锤击点的响应，分析试验件第一阶模态，得到叶片模态阻尼。需注意，模态试验加窗后时域信号得到的阻尼是过估计的。因此，为实现无泄漏测量，试验时响应不加指数窗，通过增加系统采样时间的方式，使响应有足够的时间衰减。

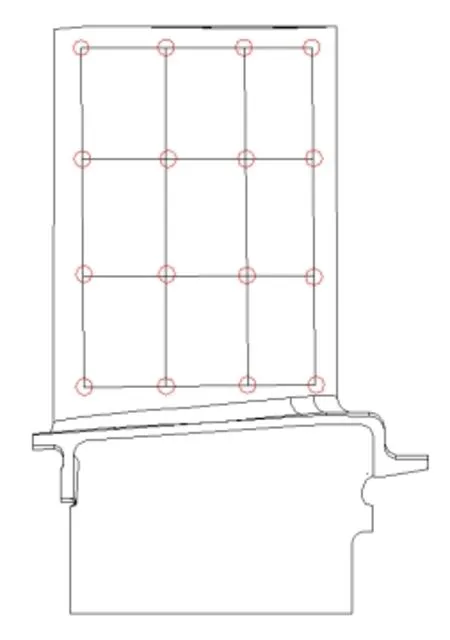
图3 锤击法敲击点Fig.3 Excitation point of hammering method

应变响应试验利用电磁振动台进行，应变片粘贴在叶片一弯最大应力点位置，用正弦慢扫描法激励，记录2 000～3 000 Hz 范围(覆盖叶片一弯频率)内应变片的应变响应曲线。为保持每次扫描时振动台的激振力不变，采用闭环控制系统；在振动台台面安装加速度传感器，将台面加速度接入数采系统，作为控制信号。经控制系统控制，台面加速度在慢扫描过程中始终为a。闭环试验系统简图见图4，真实试验系统见图5。

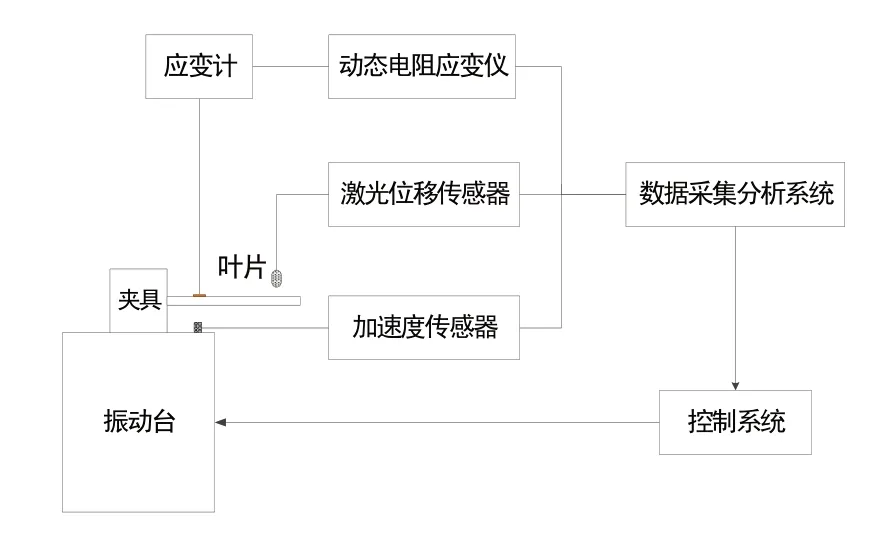
图4 闭环试验系统简图Fig.4 Schematic diagram of closed-loop test system

图5 真实试验系统Fig.5 Test system

3 试验结果及分析

根据高压涡轮叶片工作时的共振分析，第一阶振型共振转速为7 650 r/min，此时封严片离心力为66 N。由于叶片状态是确定的，即共振转速大致确定，试验通过调整阻尼片压紧力来获取最优阻尼效果。试验中选取0、50 N、100 N、200 N共4个等级进行试验。

3.1 正压力对模态阻尼比的影响

在模态试验中发现，在2 000～3 000 Hz 范围内存在两个共振峰值，见图6，一个频率在2 100～2 200 Hz 之间，另一个在2 500～2 600 Hz 之间。为确定叶片一阶共振频率，对三联装叶片进行频率测量。为排除阻尼测量系统耦合频率，利用非接触式振动测量系统进行测频；激励方式采用声激励。图7 示出了非接触式振动测量系统的试验安装状态，测频结果见图8。结果表明，叶片一阶频率在2 600 Hz 附近，因此，阻尼试验系统中2 100～2 200 Hz 的振动频率为系统耦合频率。

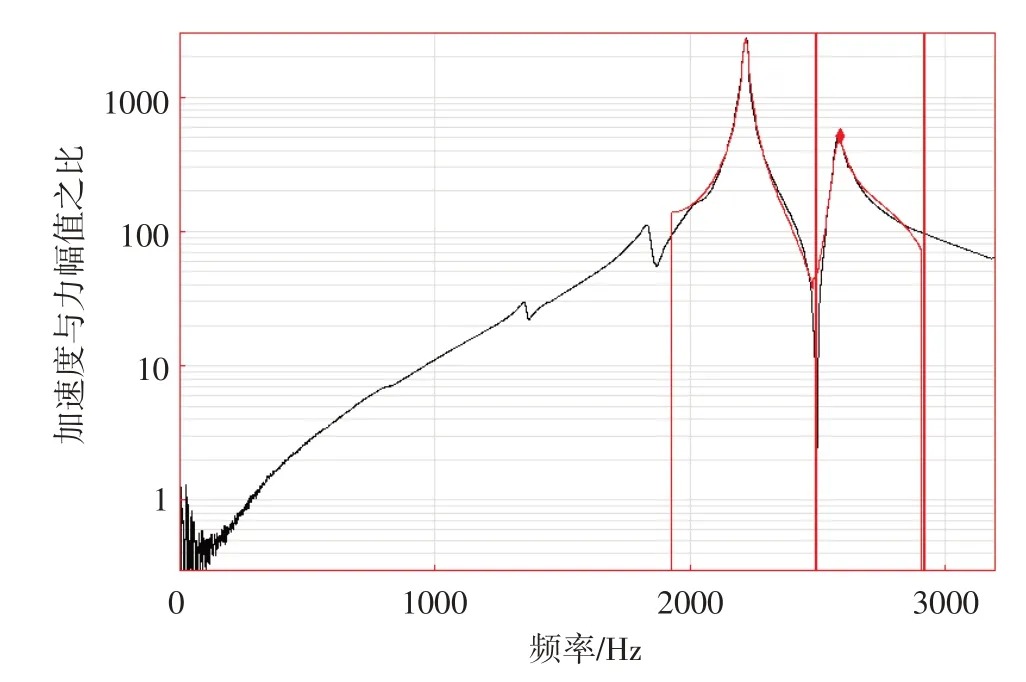
图6 频响函数Fig.6 Frequency response function

图7 非接触式振动测量系统Fig.7 Non-contact vibration measurement system

图8 叶片测频结果Fig.8 Frequency measurement result of blade

表1给出了缘板阻尼片受不同压紧力时叶片的模态阻尼试验结果。可看出，在0～200 N的压紧力范围内，叶片阻尼比随压紧力的增大而增大，且无收敛现象；叶片的一阶共振频率随压紧力的增大而增大，表明叶片刚度随压紧力的增大而增大。

表1 不同压紧力叶片的模态阻尼Table 1 Damping of blades with different pressure

3.2 压紧力对叶片动态应变的影响

在应变响应曲线试验中，通过闭环控制保持振动台激振力不变，在2 000～3 000 Hz 范围，对叶片进行正弦慢扫描激励获得阻尼片不同压紧力时叶片的应变响应曲线，如图9所示。表2给出每条曲线的最大应变及相对于无缘板阻尼片的应变降幅。从图9和表2可以得出随着压紧力的增加，叶片根部的应变先减小后增大，这是由于叶片的响应幅值是刚度和阻尼共同作用的结果。因此，存在一最优压紧力，即最优的阻尼片质量，使叶片振动应变最小。该压紧力在100 N 左右，原结构阻尼片在一阶共振时的压紧力约为66 N，与试验存在一定差异。

表2 不同压紧力叶片的模态阻尼Table 2 Damping of blades with different pressure

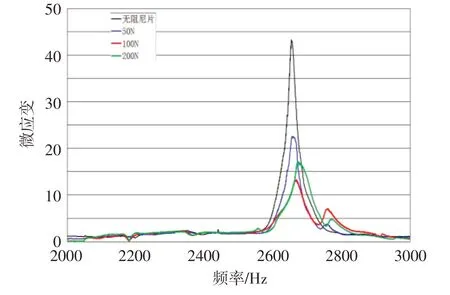
图9 应变响应曲线Fig.9 Strain response curve

根据半功率法，利用应变响应曲线计算一弯振动的阻尼比，计算方式如下：共振峰值处频率为ω0，幅值为ε，根据峰值，在响应曲线中找到半功率点，即0.707ε处的频率ω2和ω1。根据公式(1)计算叶片的阻尼比ξ，结果见表3。由表可知，在0～200 N 的压紧力范围内，叶片阻尼比随压紧力的增大而增大，此结论与模态试验的一致。

表3 不同压紧力叶片一弯振动阻尼比Table 3 First order vibration damping of blades with different pressure

4 结论

通过三联装发动机真实高压涡轮叶片的阻尼效果试验，验证了缘板阻尼片是一种有效的涡轮叶片减振措施。研究发现，随着阻尼片和缘板间压紧力的增加，叶片一阶共振频率和模态阻尼随之增加；在4 个压紧力状态中(0，50 N，100 N，200 N)，缘板阻尼片和缘板间的压紧力在100 N附近存在一最优压紧力，使叶片一弯振动应力最大点的应变响应最小；该力大小与现有阻尼结构在叶片一阶振动时的压紧力存在一定差异。为此，在后续阻尼片设计中应结合试验确定最优压紧力，通过调整缘板阻尼片质量、材料等影响因素，以达到最佳阻尼效果。