基于LSTM-GCN的PM2.5浓度预测模型
2022-10-28马俊文严京海孙瑞雯刘保献
马俊文,严京海,孙瑞雯,刘保献
北京市生态环境监测中心,大气颗粒物监测技术北京市重点实验室,北京 100048
在环境监测部门开展空气质量监测预报分析业务中,目前采用的主流空气预报分析模型仍然主要是空气数值预报模型。从研究大气流体运动学和应用大气内部流体物理学的规律关系出发,例如利用大气流体动力学、热力学等,用传统数理分析方法建立相应的具体数学大气物理规律模型,然后可以借助大型高性能计算机的计算能力,建立空气污染物浓度的动态分布运输和扩散数值预测模型。例如:XU等[1]基于尺度空气质量模式系统(CMAQ)提出了CMAQMOS模型,很好纠正了CMAQ中平均污染物排放清单所导致的系统性预测误差;CHUANG等[2]应用结合化学的天气研究与预测模型(WRF-Chem-MADRID)对美国东南部地区空气质量进行预测,结果显示在臭氧和可吸入颗粒物预测中表现良好。
近年来,研究人员尝试基于机器学习的深度学习算法预测PM2.5浓度。例如,在分析时间特征维度,王玮等[3]开展了GRU神经网络在可吸入颗粒物预测中的应用研究,白盛楠等[4]开展了LSTM神经网络在可吸入颗粒物浓度预测中的应用研究。然而,由于空气质量在时间维度具有很强的季节性,因此,研究人员开始将季节性分解算法和深度学习算法相结合,开展了PM2.5浓度预测模型的研究。例如,刘铭等[5]提出EMD分解算法和LSTM算法的组合算法EMD-LSTM,开展了PM2.5浓度预测模型研究;刘炳春等[6]提出小波分解变换算法Wavelet和LSTM算法的组合算法Wavelet-LSTM,开展了空气污染物浓度预测模型研究;王晓飞等[7]提出Prophet分解方法和LSTM的组合算法Prophet-LSTM,开展了PM2.5浓度预测模型研究。
但是,空气质量监测数据除了具有时间特征外,还具有空间特征,随着污染物传输过程以及气象因素的影响,各监测站的监测数据具有很强的空间传输演化特征。因此,研究人员开始关注基于时空特征的PM2.5预测模型。例如,宋飞扬等[8]利用KNN算法提取目标站点空间因素,提出KNN算法和LSTM算法的组合算法KNN-LSTM,开展了PM2.5浓度预测模型研究;刘旭林等[9]将地理空间网格化,利用CNN提取空间特征,提出CNN和Seq2seq的组合算法CNN-Seq2seq,开展了未来1 h PM2.5浓度的预测研究。
现有研究中时间特征提取基本是使用LSTM模型实现,空间特征提取基本是将非欧氏距离空间的监测站分布数据通过地理空间网格化后转换到欧氏距离空间,然后利用面向欧氏距离空间的二维卷积神经网络或KNN算法提取空间特征。2017年,Thomas Kpif提出了专门面向图提取图结构特征的图卷积神经网络(GCN),可以直接用于处理非欧氏距离空间监测站地理分布数据。黄伟建等[10]利用图卷积神经网络改进门控循环单元网络的输入部分,提出面向空气质量的时空混合预测模型。但是,该时空混合预测模型并未分别提取时间特征和空间特征。因此,本文基于LSTM算法构建时间特征提取组件,基于GCN算法构建空间特征提取组件,然后将时间特征和空间特征进行联合,提出预测未来1 h PM2.5浓度的LSTM-GCN组合模型。
1 LSTM-GCN组合模型构建
1.1 LSTM模型
机器学习领域的深度学习网络算法主要有3类:第一类是循环神经网络,适用于处理序列数据;第二类是卷积神经网络,适用于处理图形图像数据;第三类是全连接神经网络,适用于解决分类问题。其中,LSTM网络是循环神经网络的主要变体之一,它在充分继承了循环神经网络递归运算优点的同时,能够很好地解决目前循环神经网络在应用深度机器学习算法过程中,产生的梯度递归消失和梯度递归爆炸问题。
LSTM结构的核心思想是在循环神经网络基础上,引入一个叫单元状态的连接,最后的状态不再简单地存储,而是通过LSTM神经网络的训练机制来选择更新状态。LSTM 的训练机制是通过遗忘门、输入门和输出门来控制信息的删减或增加[11]。
1.2 GCN模型
GCN是一种基于图数据的深度学习方法,其核心思想是学习一个映射函数,可以使图中的节点能够聚合自身和邻居节点的特征,生成节点的新表示。卷积神经网络可以很好地处理欧氏空间数据以提取空间特征,对于非欧氏空间里的图数据,可以使用GCN提取空间特征。

(1)

第二步是提取特征矩阵X的空间信息,具体换算方式见式(2)。
(2)
式中:σ(·)为激活函数;W(i)为第i层权值矩阵;H(i)为第i层的激活值;H(0)=X。
1.3 LSTM-GCN组合模型
设计LSTM-GCN组合模型结构如图1所示。
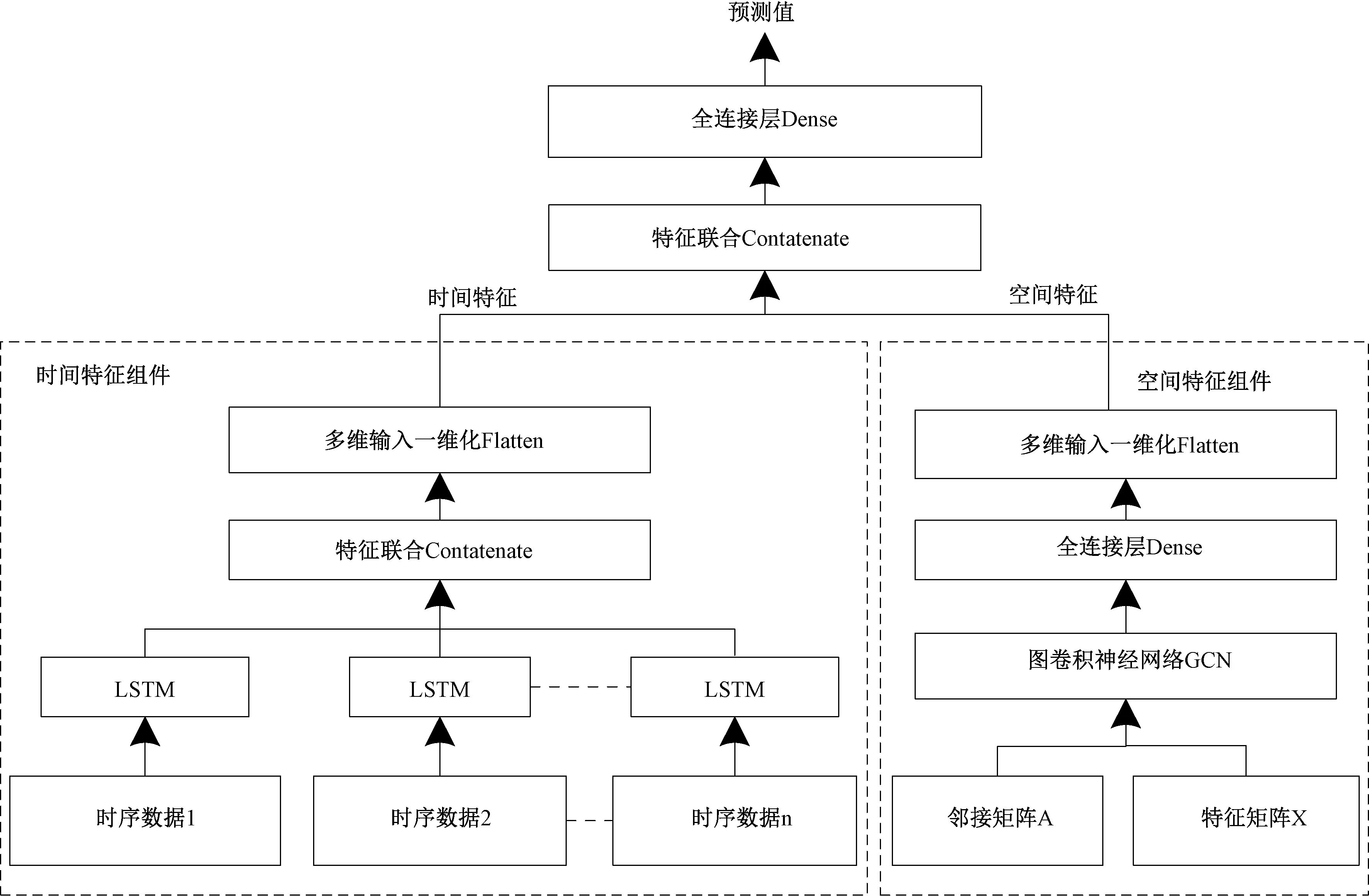
图1 LSTM-GCN模型结构Fig.1 LSTM-GCN model structure
图1中,LSTM-GCN模型包含时间特征组件和空间特征组件。时间特征组件的输入是多条时序数据,针对每条时序数据应用LSTM模型,然后将其输出合并于特征联合层,由多维输入一维化层输出所提取的时间特征;空间特征组件的输入是邻接矩阵A和特征矩阵X,然后经过GCN模型、全连接层后,由多维输入一维化层输出所提取的空间特征。最后,将时间特征和空间特征进行特征联合后,经全连接层输出预测值。
选择均方根误差(RMSE)和平均绝对误差(MAE)为模型预测效果评价指标,具体换算见式(3)和式(4)。
(3)
(4)

2 时空趋势分析和数据预处理
以北京市35个空气质量监测站2018—2020年PM2.5小时监测数据、气象监测数据、站点分布经纬度数据为样本,首先分析PM2.5时空变化趋势,然后构建LSTM-GCN模型输入数据和预测数据。
2.1 时空趋势分析
Prophet时序模型是Facebook公司于2017年发布的,它可以分解出时序数据的趋势,且弥补了传统时序模型对时序数据过于局限、需要填充缺失值、模型不灵活等不足。因此,基于该模型分解35个监测站PM2.5浓度数据的趋势分量,然后按年计算趋势分量的均值,绘制用于表征时空趋势的雷达图,如图2所示。

图2 时空趋势图Fig.2 Temporal and spatial trends
从图2可知,2018—2020年,在时间趋势方面,除了第15#站点的趋势分量年均值在2018年较低以外,其余34个站点的趋势分量年均值均随时间逐年下降;在空间趋势方面,站点之间的趋势分量年均值相对变化趋势各年基本一致。其中,第15#站点在2018年进行了停站改造,影响了数据完整性,导致趋势分量年均值偏低。
2.2 时间特征组件输入数据和预测数据构建
假设基于t时刻之前的连续24 h PM2.5浓度数据,预测t时刻PM2.5浓度,则设计构建时间特征组件输入数据以及对应的模型预测数据的程序流程分6个步骤。
1)对PM2.5小时数据按时间顺序排序,数据有35列,分别对应35个监测站。
2)剔除极大和极小异常值,按列执行归一化,即对每个监测站的PM2.5小时数据分别进行归一化。
3)定义存储时间特征组件输入数据的变量M,存储LSTM-GCN模型预测数据的变量Y。
4)建立滑动窗口,窗口大小为25,并置于数据顶端。
5)提取滑动窗口内的数据,前24条数据追加到变量M,第25条数据追加到变量Y。
6)如果窗口滑动到达数据底端,则终止程序,否则,滑动窗口向下一小时滑动,返回第5步。
时间特征组件输入数据是35个站点t时刻之前的连续24 h PM2.5浓度数据,用Mk表示,则其数据格式如式(5)所示。
(5)
式中:k=1,2,…,35。
LSTM-GCN的预测数据是35个站点t时刻PM2.5浓度预测值,用Yt表示,则其数据格式如式(6)所示。
(6)

2.3 空间特征组件输入数据构建
空间特征组件用于提取35个监测站在空间分布上的演化趋势特征。其中,监测站在北京市的空间分布情况如表1所示。

表1 35个站点空间分布Table 1 Spatial distribution of 35 stations
空间特征组件的输入数据有站点分布图和站点特征数据。站点分布图是以站点为顶点,以站点之间的距离倒数为边权构建的加权无向图,站点分布图用邻接矩阵表示,其数据格式如式(7)所示。
(7)
式中:yij为站点i和站点j之间地理距离的倒数,yii=0;i,j=1,2,…,n;n=35。
站点之间的地理距离可以由站点经纬度数据计算得到,假设站点P的经纬度为(P1,P2),站点Q的经纬度为(Q1,Q2),则计算站点P和站点Q之间的地理距离D,具体换算方式见式(8)。
D=R×arccos[sin(P2)×sin(Q2)+
cos(P2)×cos(Q2)×cos(P1-Q1)]×π/180
(8)
式中:R为赤道半径,取值为6 371.004 km。
站点特征数据是t-1时刻每个站点所具有的特征,假设每个站点有m个特征,则形成的特征矩阵如式(9)所示。
(9)
式中:zij是站点i的第j个特征;n=35。
因为每个监测站点除了监测PM2.5外,还监测相关气象数据,且气象条件的变化对PM2.5有影响[12],因此,使用PM2.5、风速、风向、温度、湿度构建监测站点的特征数据。数据预处理方法:对PM2.5、风速、温度、湿度4列数值型数据,剔除异常数据后分别执行归一化;对风向数据,按照东、南、西、北、西北、东北、东南、西南8个方向,使用独热编码(One-Hot Encoding)方法,编码为由0和1组成的8位数据,每个数据位代表1个方向。例如,若8位数据中代表方向东的数据位为1,代表其他方向的数据位为0,则表示风向为东风。以上2类数据按列合并后,形成包含12列的特征数据。
按照时间维度依次提取35个站点同一时刻的特征数据,形成特征矩阵,则其阶数为35×12阶,行代表35个监测站点,列代表监测站点特征。
LSTM-GCN模型输入和输出矩阵的阶数如图3所示。
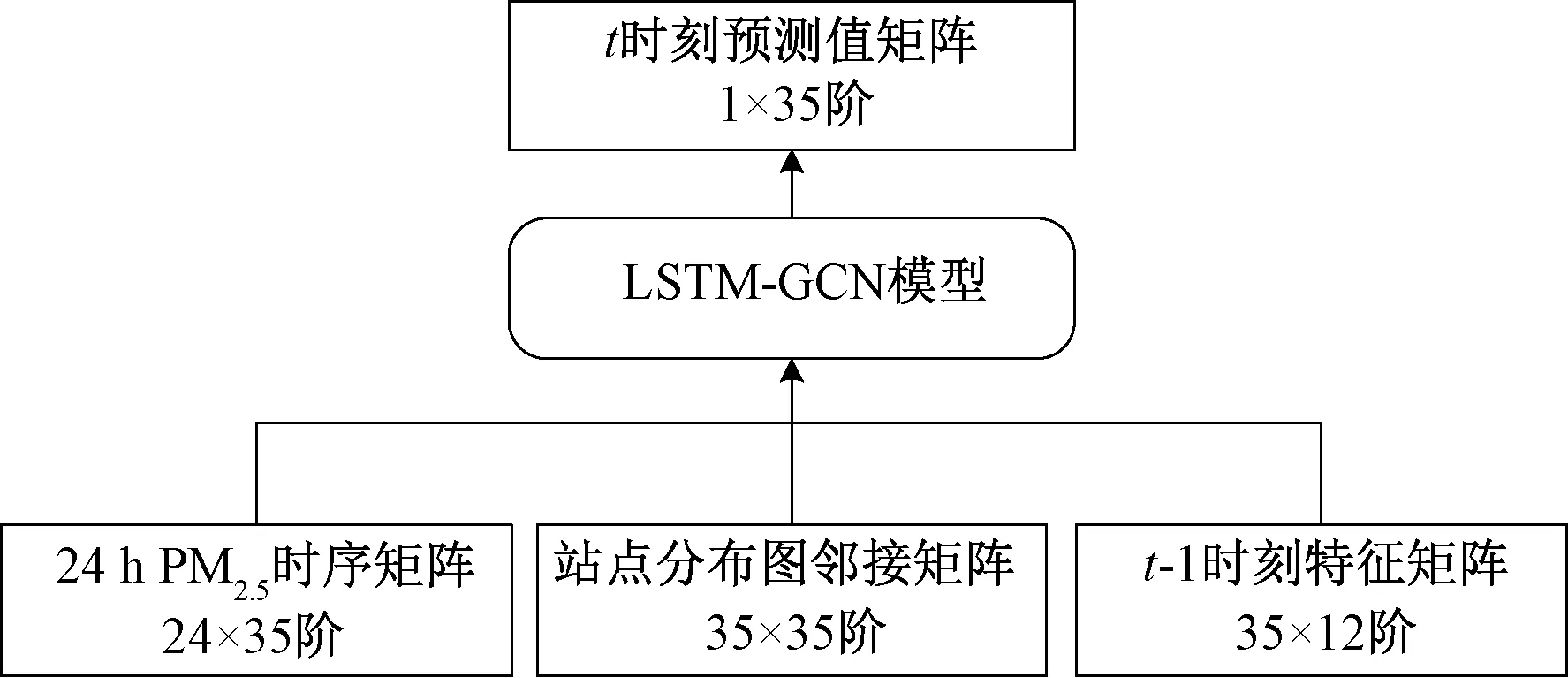
图3 模型输入/输出矩阵阶数Fig.3 Input/output matrix order of model
图3中,LSTM-GCN模型输入有3个矩阵,分别是24×35阶的PM2.5时间序列矩阵、35×35阶的站点分布图邻接矩阵、35×12阶的监测站特征矩阵,输出预测值是1×35阶的矩阵。
3 仿真实验
本文实验基于TensorFlow开发,它是一个基于Python语言的较为成熟的开放源代码的深度学习框架,应用较为广泛,尤其在自然语言处理、推荐系统、图形分类、音频处理等领域应用较为丰富[13]。
模型化的开发工具可以选择Keras来实现,它是一个可以在Tensorflow里被导入、能够被用于开发深度学习模型的高级API,在极大程度简化模型的基本构建设计过程和模型训练方法的同时,还可以完全兼容在Tensorflow里已有的模型开发相关的绝大部分功能,具有易于模块化、可弹性组合、用户友好、易于进行扩展的四大优点[14]。此外,针对复杂模型,可以使用Keras函数式API进行定义,然后把模型看作层,使用传递张量的方法来调用模型。
本实验除了实现LSTM-GCN模型外,还分离时间特征组件和空间特征组件,形成2个独立的LSTM模型和GCN模型,作为评估LSTM-GCN模型的对比模型。
模型训练和预测程序流程图如图4所示。

图4 模型训练和预测程序流程图Fig.4 Flow chart of modeltraining and prediction
从图4可见,样本数据预处理后,按照时间顺序排序,划分前80%为训练数据,后20%为测试数据,设定模型激活函数为ReLU[15],损失函数为均方误差(MSE),优化方法为自适应运动估计算法(Adam)。
同时,将时空地理加权回归模型(GTWR)作为对比模型,GTWR是一种通过构建时空非平衡关系的局部线性回归模型,设置模型解释变量为t时刻PM2.5浓度、风速、温度、湿度,因变量为t+1时刻PM2.5浓度。
根据每个目标站点上实际值和4个目标模型的预测值,分别计算所对应的4个模型的评估指标RMSE和MAE,计算结果如图5和图6所示。

图5 各监测站RMSE对比图Fig.5 RMSE comparison of monitoring stations
从图5和图6可知,4个模型对35个监测站的预测精度具有较为一致的波动趋势,且LSTM-GCN模型预测精度最高,GCN模型预测精度最差。
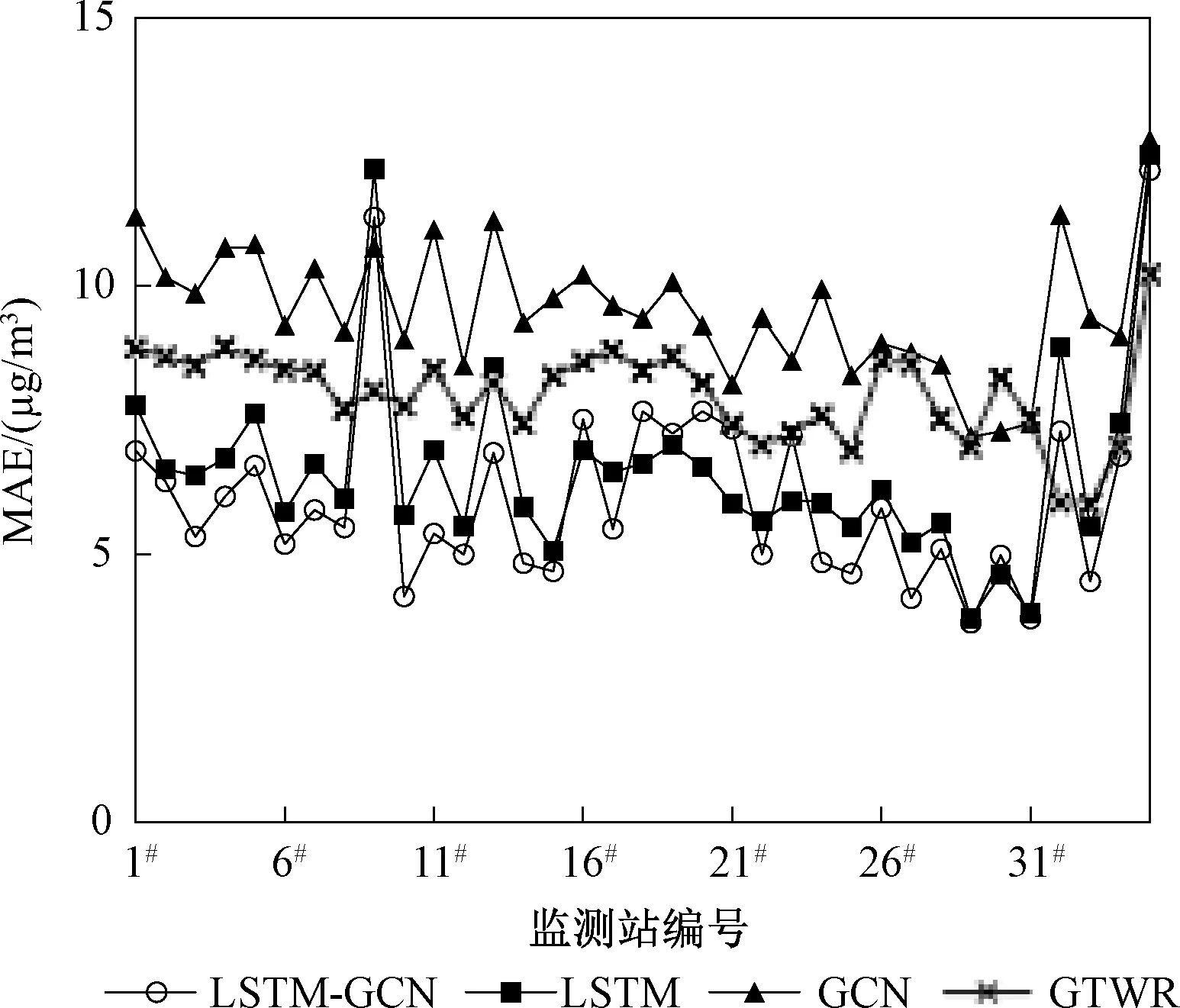
图6 各监测站MAE对比图Fig.6 MAE comparison of monitoring stations
计算35个站点RMSE和MAE的平均值,结果如表2所示。

表2 模型评估结果Table 2 Model evaluation results
从表2可见,LSTM-GCN模型评估结果优于LSTM模型、GCN模型、GTWR模型,相较于LSTM模型RMSE、MAE分别降低了11.68%、7.34%;相较于GCN模型RMSE、MAE分别降低了40.22%、36.37%;相较于GTWR模型RMSE、MAE分别降低了17.52%、23.69%。
以1#站点为例,抽取同一时间的真实值和4个模型的预测值,绘制曲线如图7所示,以展示时间维度模型预测效果。
从图7可知,在时间维度,4个模型的预测值基本随着实际值波动,且趋势较为一致,预测效果较好。

图7 1#站PM2.5预测效果Fig.7 PM2.5 prediction effect of 1# station
随机选择某时刻,获取35个监测站实际值和预测值,绘制曲线如图8所示,以展示空间维度模型预测效果。
从图8可知,在空间维度,4个模型预测值的波动幅度和演化趋势同实际值较为一致,预测效果较好。

图8 35个站PM2.5预测效果Fig.8 PM2.5 prediction effect of 35 stations
应用LSTM-GCN模型预测北京市35个监测站2021年1—7月的PM2.5数据,随机抽取部分时间的预测值和实际值,绘制对比图,其中6个站的对比图如图9所示。

图9 6个监测站的LSTM-GCN预测值和实际值对比图Fig.9 Comparison between LSTM-GCN predicted valueand actual value of six monitoring stations
从图9可知,6个监测站的预测值很好地拟合了实际值,说明预测效果较好。
4 结论
本文提出的LSTM-GCN模型同时考虑空气质量数据时间特征和空间特征,从模型预测和评估结果来看,能够进行PM2.5数据的预测,且预测精度比LSTM模型、GCN模型、GTWR模型均有所提升。LSTM-GCN模型在2021年1—7月的PM2.5浓度预测效果表明,该模型具有一定的可用性。
但是,LSTM-GCN模型没有分解PM2.5的季节性,后续可以再研究叠加一种适用的季节性分解算法,并增加LSTM和GCN的层数,进一步优化模型。
LSTM-GCN模型相比传统数值模型具有数据需求少、运行速度快、计算资源需求少等优势,有望在短时预测、数据审核、异常数据判定等业务中成为一种技术支撑手段。
