基于闭马尔可夫排队网络的多机型舰载机出动仿真
2022-10-28胡锦鹏宋庭新
胡锦鹏, 宋庭新
(湖北工业大学机械工程学院, 湖北 武汉 430068)
舰载机作为航母编队执行作战任务的重要力量,其出动能力是衡量航母编队作战能力的关键指标。Jewell 等[1]对高强度演习中的演习前准备、整个演习作业流程等几个方面进行了深入研究,得到各种因素可以支持的最大出动架次;Dennis等[2]基于Fork-Join闭排队网络模型对飞机出动能力进行了研究;郑茂等[3]运用基于蒙特卡洛的仿真实验对舰载机高峰出动架次率进行计算; Jenkins 等[4]针对飞机的架次率运用均值分析的启发式算法进行了研究。董文洪等[5]基于马尔科夫链分析计算出单机型舰载机的出动能力。杨甫勤等[6]为获得多机种(型)军用飞机的出动架次曲线及相关排队参数,建立了相应的闭排队网络模型。陈成等[7]运用基于智能体及离散时间的建模方法,建立舰载机出动流程仿真模型,对架次率进行分析计算。彭雅欣等[8]建立仿真SGR计算模型,针对其需重复计算以降低计算结果随机性的问题,得到BP-SGR计算模型,并使用该模型进行甲板资源配置优化研究。上述研究从蒙特卡洛、均值分析、排队论或资源配置等方向入手,对舰载机的出动能力进行了分析。而对于从舰载机执行作战任务的实际流程以及多机型舰载机出动特点的建模要么比较少,要么较为单一。本文从多机型舰载机出动回收全流程出发,结合排队论,运用基于马尔可夫链状态转移过程的研究方法,将其概率转移矩阵作为模型参数考虑,建立多机型舰载机闭排队网络模型,仿真更贴合实际。通过仿真程序,获得多机型舰载机持续出动架次曲线以及其他相关排队参数。
1 多机型舰载机出动回收模型的建立
1.1 舰载机出动回收过程
舰载机出动回收流程较为复杂,其中每一环节都是影响舰载机架次率的重要因素,所以,对其出动回收过程的分析很有必要。对于舰载机的一个出动架次而言,舰载机起飞出动后,不论执行任务耗时多久,若没有着舰,就视为同一架次;当该舰载机着舰,则该架次结束。舰载机的出动架次生成过程可以划分为很多部分,其中甲板作业最为重要。所以现今航母一般设定飞行甲板作业周期来提高舰载机出动架次率。飞行甲板作业周期可分为1+00(1 h 0 min),1+15(1 h 15 min),1+30(1 h 30 min),1+45(1 h 45 min),2+00(2 h 0 min)等多种,舰载机作业一般按照该周期来确定。而根据在空时间的差异,舰载机作业周期又可划分成单周期或双周期两种作业模式(图1)。
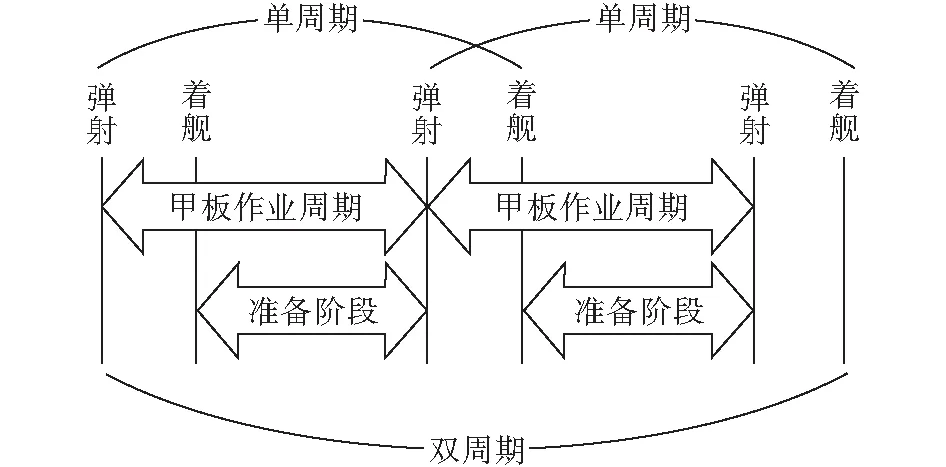
图1 舰载机作业周期
舰载机的出动回收流程基于作战任务的驱动。如图2所示,在某一舰载机收到作战任务命令后,首先判断该舰载机的当前位置,若该舰载机当前停驻于飞行甲板区则直接牵引至舰面保障站;若该舰载机当前停驻于机库,则先通过升降机及调运系统将该舰载机调运至飞行甲板后,再牵引到舰面保障站。起飞前保障工作包括加油、供电、充氧、充氮、挂弹、起飞前检查、维修检测等环节。待保障工作完成后,舰载机将滑行至过渡站位进行准备,再由过渡站位至弹射站位弹射起飞;起飞后执行相应作战任务,任务完毕后返航,着舰阻拦。着舰后进行飞行后的故障检测,若舰载机出现故障,则将其牵引至舰面保障站或机库进行维修;若未出现故障,则根据舰面当前驻留条件,牵引至舰面保障站或机库进行维护,等待下一次作战任务。

图2 舰载机出动回收流程
1.2 基于马尔可夫转移概率矩阵的多机型舰载机出动回收分析
马尔可夫过程(Markov Process)是一种特殊的随机过程[9]。对于多机型舰载机持续出动过程而言,不同作业时期舰载机所处的状态不同,且这些状态个数至多是可数的(或称可列的)。如果已知舰载机当前时期所处状态,则该时期之前舰载机处于何种状态,对预测舰载机该时期之后所处状态不起作用,即当前时期下舰载机状态参数的概率分布只与该时期相邻的上一时期状态相关,与舰载机更早的状态不相关,具有马尔可夫性(或称无后效性)。因此,可以用马氏过程来分析多机型舰载机的持续出动问题。
设舰载机出动过程
X={Xn(ω),n∈T}
其中T为甲板周期。用Xn=i表示时刻n舰载机出动过程X处于状态i这一事件,称
pij(n)=P(Xn+1=j|Xn=i)
(1)
为在舰载机“Xn=i”状态出现的条件下,舰载机“Xn+1=j”状态出现的条件概率,又称它为舰载机出动过程X={Xn(ω),n∈T}的一步转移概率,由它来表示舰载机第n步转移到第n+1步的转移概率。且对任意的非负整数i1,i2,…,in-1,i,j及一切n≥0,都存在
P(Xn+1=j|Xn=i,Xk=ik,k=1,2,…,n-1)=P(Xn+1=j|Xn=i)=pij(n)
(2)
则称舰载机出动过程X={Xn(ω),n∈T}为马尔可夫链。当pij(n)与初始时刻n不相关时,舰载机出动过程X={Xn(ω),n∈T}是一齐次的马尔可夫链,且称式(2)为马尔可夫性。若将“Xn=i”看作舰载机的“现在”,将Xn+1=j看作舰载机的“将来”,“Xk=ik,k=1,2,…,n-1”看作舰载机“过去”,则式(2)表示在已知舰载机“现在”的条件下,其“将来”与“过去”是独立的。易知
(3)
称
(4)
为舰载机出动过程X的一步转移矩阵。式(3)表明矩阵P中每个元素非负且矩阵中每一行之和都为1。
又称

(5)
为舰载机出动过程X的n步转移概率。而
(6)
为舰载机出动过程X的n步转移矩阵。且具有如下性质:
(7)
利用P(AB|C)=P(A|C)P(B|AC)及马尔可夫性,并注意P(∪k{Xn=k})=1可得到Kolmogorov-Chapman方程,其中∀i,j∈E
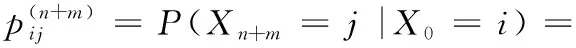
(8)
上式也可写成
P(n+m)=P(n)P(m)
(9)
显然,舰载机的持续出动过程X={Xn(ω),n∈T}具有有限种状态(本文中为10种),具有马尔可夫性,且为一个有限状态的马尔可夫链(Markov)。上述式子表明,由马尔可夫链的一步转移概率可确定其k步转移概率,则对于舰载机出动流程来讲,其任意时间步上的转移概率和绝对概率分布,都可由其状态转移概率和初始状态的概率来确定,由此来分析舰载机持续出动的状态转移概率矩阵,并为后续模型的建立奠定基础。
1.3 多机型舰载机闭排队网络模型
多机型舰载机从弹射起飞到执行作战任务后着舰,要经历一系列复杂的保障环节。基于排队论思想[10],可将不同机型的舰载机看作不同类型的顾客,将舰载机出动回收流程的各工作环节看作多个服务节点,并基于上述流程分析建立一个多类舰载机在多个服务节点排队的闭排队网络。如图3所示,舰载机在某一服务节点i接受服务后服从一定概率Pij转移至下一服务节点j。例如:某机型舰载机在服务节点1~3完成加油、加氧及挂弹服务后,到服务节点4进行故障检测,若该舰载机检测出故障,则以概率P49转移至维修节点(服务节点9)进行维修服务;若该舰载机未检测出故障,则以概率P45转移至弹射节点(服务节点5)进行弹射起飞服务。各机型舰载机在各服务节点间的初始转移概率用转移概率矩阵表示为式(4),各机型舰载机持续出动状态转移概率矩阵表示为式(6)。

图3 舰载机闭排队网络
为易于建立和求解多机型舰载机出动回收仿真模型,还需对舰载机、各服务节点和各种机型舰载机的排队作出以下假设:
1)当服务点服务机制为先到先服务(FCFS)时,则服务节点i有多个(有限)服务窗口mij,对各机型舰载机的服务时间为不同参数的负指数分布;当服务机制为无限服务窗(IS)时,则服务节点i有无穷个服务窗口,即该服务节点会立刻对所有进入队列的舰载机服务。
2)系统中的舰载机不会发生坠毁事故,且发生故障的舰载机最终都能维修成功,即系统战损率为0。
3)为防止系统发生阻塞,将各服务节点的排队空间设为无穷大,即舰载机不会因为某节点繁忙而停滞于该节点的上一节点。
4)各服务节点的服务时间同时包含舰载机在该节点的服务时间和舰载机由上一节点滑行到该节点所消耗的时间。
2 仿真程序与实例分析
2.1 参数设定
本文以美海军尼米兹级航母为研究对象,其数据较为全面的舰载机是F/A-18和F-14两种机型,而且这两种机型在1997年7月20日演习中的出动架次比例占总出动架次的80%以上。因此,在本次仿真中主要考虑这两种机型。假设有36架F/A-18舰载机和12架F-14舰载机,所有舰载机均进行高峰作业,甲板作业周期为1 + 30,在F/A-18的出动架次中有80%为单周期,20%为双周期;在F-14的出动架次中有90%为单周期,10%为双周期。
除以上系统参数外,按照多舰载机闭排队网络流程(图3),设定F/A-18和F-14两种舰载机在各服务节点的服务时间及其服务窗口数目(表1)。
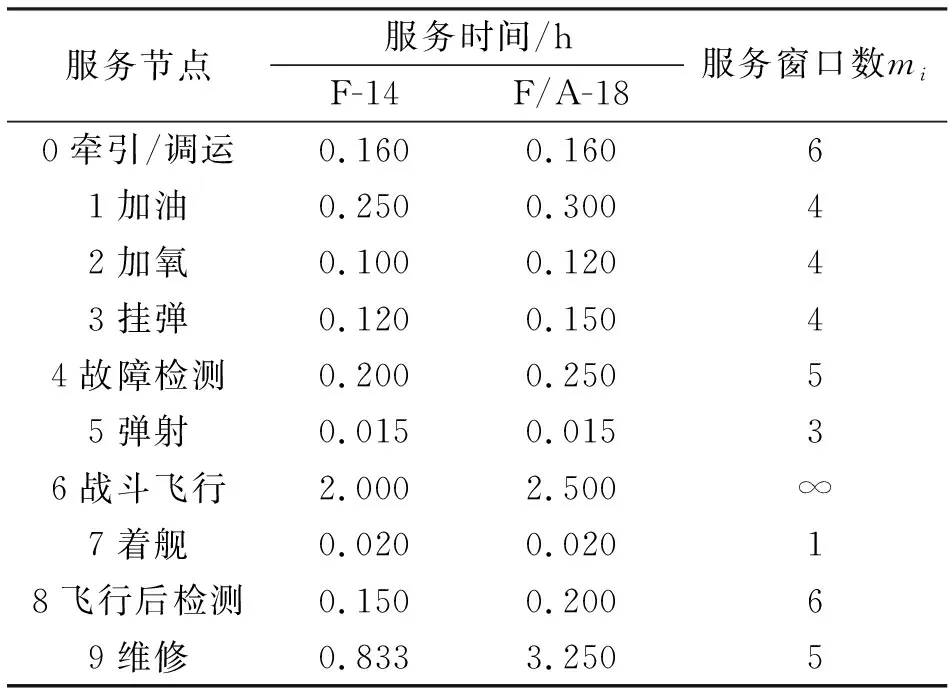
表1 多机型舰载机各服务节点参数
在各服务节点中,牵引/调运、加油、加氧、挂弹、故障检测、弹射、着舰、飞行后检测和维修等节点为先到先服务(FCFS);而战斗飞行服务节点为舰载机在空中执行作战任务,故该节点服务窗口个数可视为无穷多,所有舰载机到达该节点后无需等待可立刻接受服务,为无限服务窗(IS)。且设各节点服务时间均服从不同参数的负指数分布。两类舰载机在出动回收过程的初始状态转移概率矩阵
P=

2.2 仿真结果与分析
运用仿真软件对上述模型进行编程,最后得到诸如舰载机出动架次、舰载机在空架次,维修节点队长、排队维修飞机数等性能指标(图4~7)。图4为仿真输出的舰载机持续出动架次曲线,其飞行作业时长设定为1440 min(24 h),飞行甲板周期设定为1 + 30,作业模式设定为单周期。由图4可知,此时模型单日出动架次为199架,平均每架舰载机每天出动约4次。从文献[11]可知,美军尼米兹级航母在1997年演习中的高峰出动持续了4 d,F/A-18共计出动643架次,F-14共计出动145架次,即日均出动197架次,与本仿真结果的199架次误差仅为2架次,表明仿真精度可靠。
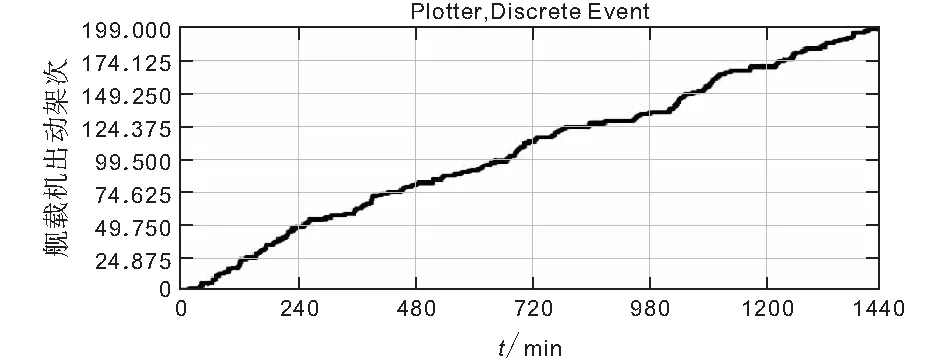
图4 舰载机出动架次

图5 舰载机在空架次

图6 维修节点排队队长
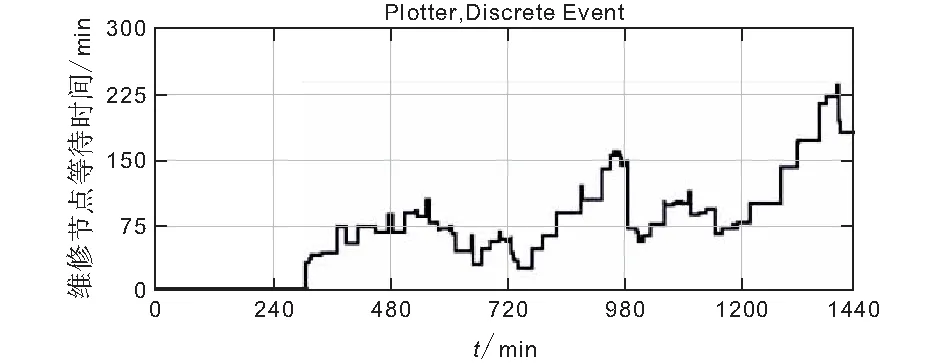
图7 维修节点等待时间
表2为各服务节点利用率及平均队长。由表2可知,加油服务节点和维修服务节点的资源利用率分别为59.1%和87.3%,平均队长分别为4.499架和8.835架,而其他服务节点的利用率都低于45%,平均队长都低于1.0,表明加油和维修两服务节点是影响两种机型舰载机出动能力提升的瓶颈,而且部分服务节点资源利用率和平均队长差异较大,表明服务窗口配置不均衡。

表2 各服务节点利用率及平均队长
由图8可知,维修服务节点和加油服务节点的利用率随服务窗数的增加而降低。

图8 维修及加油节点利用率
当维修节点的服务窗数增加较小时(m<3),维修节点的利用率变化并不大,得到的改善不明显;当m>3时,维修节点利用率才明显下降。与维修节点相比,加油节点原本利用率较低,在增加服务窗口后,加油节点利用率下降较为迅速。当加油节点服务窗口增加数达到 9 个(及以上) 时,该节点利用率低于0.2,服务能力充足,若继续增加服务窗口数,对该站的影响较低。为确定合适数量的加油节点和维修节点服务窗数,需综合分析各节点服务窗数及服务时间等因素的关系。该仿真结果可为指挥官确定加油、维修等航空保障设备的配置问题,或为优化现有配置提供参考。
3 结论
本文基于马尔可夫链分析舰载机出动回收全流程,得出多机型舰载机持续出动的状态转移概率矩阵;引入排队论,建立多机型舰载机闭排队网络模型,将分析结果作为模型参数输入,并编制了仿真模型。该仿真模型更贴合多机型舰载机出动回收的实际流程。因仿真程序忽略了某些细节,其中部分问题还需要依据航母和舰载机的真实数据来确定,但该方法实现比较方便,误差可以接受。模型可输出舰载机持续出动架次曲线,同时还得到了舰载机在空架次、维修节点排队飞机队长、维修节点排队时长等关键指标,并求出各服务节点平均队长及利用率等相关排队参数。为提高舰载机出动架次率,也可从改善瓶颈服务节点、增加服务窗数、提高节点服务效率等方面考虑。该仿真程序可用于舰载机高峰出动架次的确定及其作战能力的评估,也可为设计者优化设备配置提供参考。
