基于WT-SVM的高压电力电缆局部放电检测方法研究

陆钟华,朱 健

(国网江苏省电力有限公司扬州供电分公司,江苏 扬州 225009 )

0 引言

电力电缆是电力系统中使用的一种绝缘线路，主要用于主干线路，以实现大功率电能的传送和分配。高压电力电缆指的是电压在110～275 kV、用于电能传输和分配的绝缘电缆[1]。局部放电(partial discharge，PD)是由于绝缘劣化以及遭受破坏导致的。每次PD都会对绝缘介质造成损害。PD强度将直接影响绝缘介质损害程度。其损害程度越高，绝缘介质的绝缘强度越低[2]。PD会引发电脉冲、超声波、局部发热等现象，对于电缆的运行和使用均存在较大的安全隐患。因此，PD检测作为可及时发现PD的主要方法，对其进行相关研究非常重要。为可靠检测高压电力电缆是否存在PD现象，刘哲等[3]对电缆终端PD的信号特性进行分析后，通过建立暂态对地电压法物联网传感单元监测PD现象。该方法在应用过程中的检测效果较好，但存在一定局限性，如发生放电的位置不在电缆终端时会影响检测精度。刘孟佳等[4]分析了电磁干扰信号对PD检测的影响，并利用宽频带检测传感器和分离分类相结合完成PD检测。该方法的检测效率较高、功耗较低，但检测精度和稳定性较低，不能大范围应用。

基于此，本文结合小波变换(wavelet transform,WT) 和支持向量机(support vector machine,SVM)两种算法的优势，实现高压电力电缆PD检测。SVM算法依据监督学习完成目标的分类识别[5]。WT分析法具备变换能力，可在完成信号分析和处理的同时实现信噪分离[6]。本文结合这2种算法的优势，在最大程度保证放电信号特征的前提下去除信号中的噪声，完成信号的分类识别，实现PD检测。

1 高压电力电缆PD检测

1.1 PD检测流程

WT和SVM的高压电力电缆PD检测方法整体包含2个部分：一是PD信号采集和预处理；二是信号的特征提取和分类识别。

PD检测流程如图1所示。

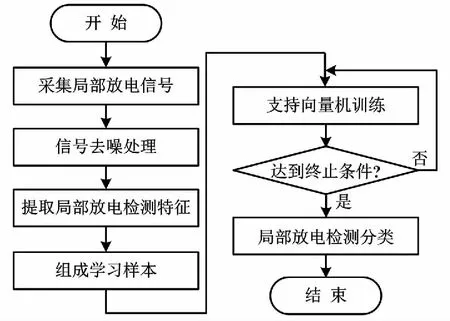
图1 PD检测流程

电缆在实际的检测过程中，采集的信号会存在不同强度的噪声。噪声会对最终检测结果造成直接影响[7]。因此，为保证在去除噪声的同时不会对PD信号造成影响，本文将WT和信息熵相结合，以改进后的WT算法(即小波熵算法)对采集的信号进行预处理，从而去除信号中的噪声。

1.2 基于小波熵的高压电力电缆PD信号降噪

本文通过小波熵算法完成高压电力电缆PD信号的降噪处理。该算法能完成噪声能量阈值的确定，依据该阈值对采集的有效信号和噪声信号进行调整[8]，修正两者的比例，从而完成降噪。

本文采用WT分析PD信号。其分析方式为多制度，以此获取信号信息，且该信息呈现差异性尺度。在此基础上，为获取小波熵的大小，对获取的信号实行量化计算。总能量为：

(1)

式中：f(j,n)为小波系数，其位于第j层；N为系数点数量。

采用式(2)描述位于第i个子区间的小波系数能量：

(2)

式中：m、M为子区间范围点。

整体能量中，第i个子区间的小波系数能量所占比例及其小波熵的计算式分别如式(3)、式(4)所示。

(3)

式中：pj,i为第i个子区间的小波系数的能量所占比例。

(4)

式中：Si为第i个子区间的小波熵。

由式(3)和式(4)可知，每个尺度信息均可作为1个信号源。因此，可采用平均划分对每个尺度小波系数进行处理，使其形成数个子区间，从而获取小波熵值。

PD信号包含低频和高频两种区域。前者以小波系数为主，而后者以噪声信息为主。如果该区域内全部都是噪声信号[9]，则噪声阈值的计算式为：

(5)

式中：Pw为PD信号。

在实际情况下，高频区域中并不全是噪声信号，也存在PD信号。因此，如果对高频区域进行处理会对PD信号造成破坏。采用小波熵值大小描述细节程度和风量分布。前者对应PD信号，而后者对应尺度空间。噪声信号含量随着小波熵值的增加而增加[10]。因此，需依据小波熵值的大小确定h(j)。

假设加入小波熵的最大区间为第i个子区间，那么可利用小波熵的最大值表示噪声值的变化关系，将其均值作为噪声值能量的阈值。则该阈值的计算式为：

(6)

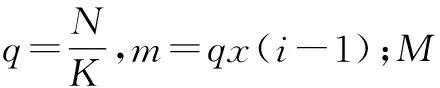
如果噪声信号覆盖PD信号中的有效信号，则表示此时信号较弱，可对频率进行计算，通过空域相关去噪方法完成。同时，将计算获取的频率由高至低排列。当相关系数发生变化时，属于模极值点且位于PD信号中的噪声能量阈值可采用h*(j)描述，以完成信号和噪声的区分[11]。

噪声能量阈值采用h*(j)描述时，能够最大程度去除PD信号中的噪声，同时可使检测结果的可靠程度显著提升[12]。详细步骤如下所述。

①C(j,n)为相关系数，属于高频尺度，且j=1。对C(j,n)实行求解，通过空域去噪方法求出归一化系数CNew(j,n)。将CNew(j,n)与C(j,n)进行对比，判断两者大小。如果前者大于或等于后者，则对PD信号信息fNew(1,n)进行保留，并确定位于n点处的小波变换值是由PD信号导致。利用n点系数替代fNew(1,n)。n点系数属于f(1,n)区间，保留该点值，将位于该点处的f(1,n)和C(j,n)归零，对PD信号的相关性信息实行搜寻。此时，f(1,n)均会保留在fNew(1,n)中，且不含有噪声。

②如果j>1，对|CNew(j,n)|和|f(1,n)|进行对比，判断两者的大小。如果前者大于等于后者，则将刚获取的PD信息采用WfNew(j,n)替代。

循环上述步骤，即可确定最佳的Th*(j)值。

1.3 PD检测

PD特征能够体现其信号的类别，并能判断信号是否为异常信号。因此，信号特征的提取直接与检测结果关联。本文采用奇异值谱对经过小波熵降噪后的电缆PD信号实行检测。其计算式为：

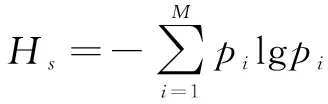
(7)

式中：pi为整个奇异谱中第i个奇异值占据的百分比。

pi的计算式为：

(8)

式中：δi为奇异谱值，属于PD信号。

对PD信号的奇异谱熵实行归一化处理，以此提升PD信号检测效率。其处理式为：

(9)

经特征提取后得出PD检测特征Xi，且Xi=[X1,X2,...,Xd]T∈Rd。PD信号的类别为yi∈Rd。由PD信号样本组成的训练集为(Xi,yi)，且i=1,2,...,n，其中，n为样本数量。采用SVM对(Xi,yi)进行映射，以构建最佳超平面，使距离最小化。以此可完成线性函数的构建。其计算式为：

f(x)=wΦ(x)+b

(10)

式中：Φ(x)为函数；w和b分别为权值和偏置。

在对两者实行求解时，会存在部分样本点误差较大的情况。因此，本文引入松弛因子进行调整。计算式为：

(11)

式中：ε为损失函数，且为不敏感。

采用式(12)描述最优超平面获取问题。

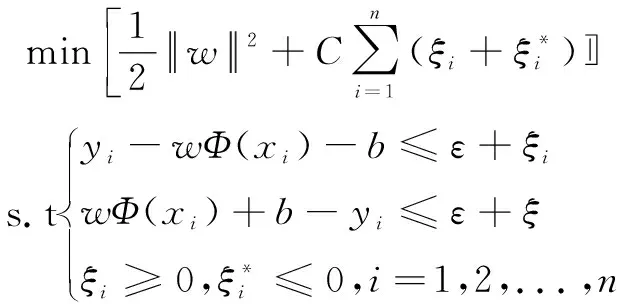
(12)

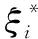
向式(12)中引入Largrange函数，完成式(12)的转化，使其形成对偶形式。其计算式为：

(13)

式中：α和α*均为乘子，属于Largrange函数。

采用式(14)表示式(13)的约束条件：

(14)

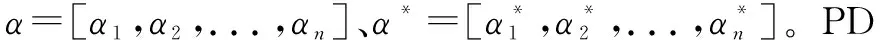
(15)

式中：K(xi,xj)为核函数。

(16)

2 测试结果与分析

为测试本文方法在高压电力电缆PD检测方面的相关应用情况，采用无线传感器对某地区220 kV的电缆PD信号进行采集。采集的样本数量为1 500个。采集的信号包含自然环境中的不同大小的噪声。将采集的信号通过服务端接口传送至服务器，并存储至MATLAB软件内。利用该软件向采集的信号输入包括电晕、沿面、气隙和悬浮的4种PD现象模拟信号。输入数量均为25个，则总样本数量为1 600个。

参数优化取值测试结果如图2所示。在进行PD检测测试前，需确定最佳惩罚参数和核函数的取值，以PD的识别精度值作为衡量标准，测试在2个参数取值不同时PD的分类识别结果。

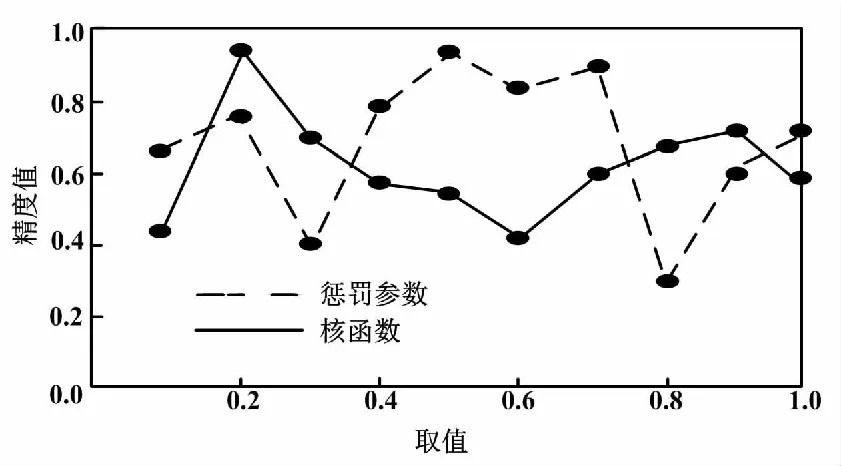
图2 参数优化取值测试结果

根据图2的测试结果可知：惩罚参数和核函数的取值不断增加，PD的识别准确率随之发生不同的波动变化，在两者取值分别为0.5和0.2时识别准确率最高。因此，本文确定两者的最佳取值为0.5和0.2，并用于后续试验。

为判断本文方法的降噪效果，采用本文方法对电晕、沿面、气隙、悬浮4种PD信号进行降噪处理，并将降噪后的信号与降噪前的原始采集信号进行对比，以此衡量本文方法的降噪效果。但是由于篇幅有限，仅随机呈现其中2种PD信号的降噪结果。

气隙信号降噪前后的测试结果如图3所示。

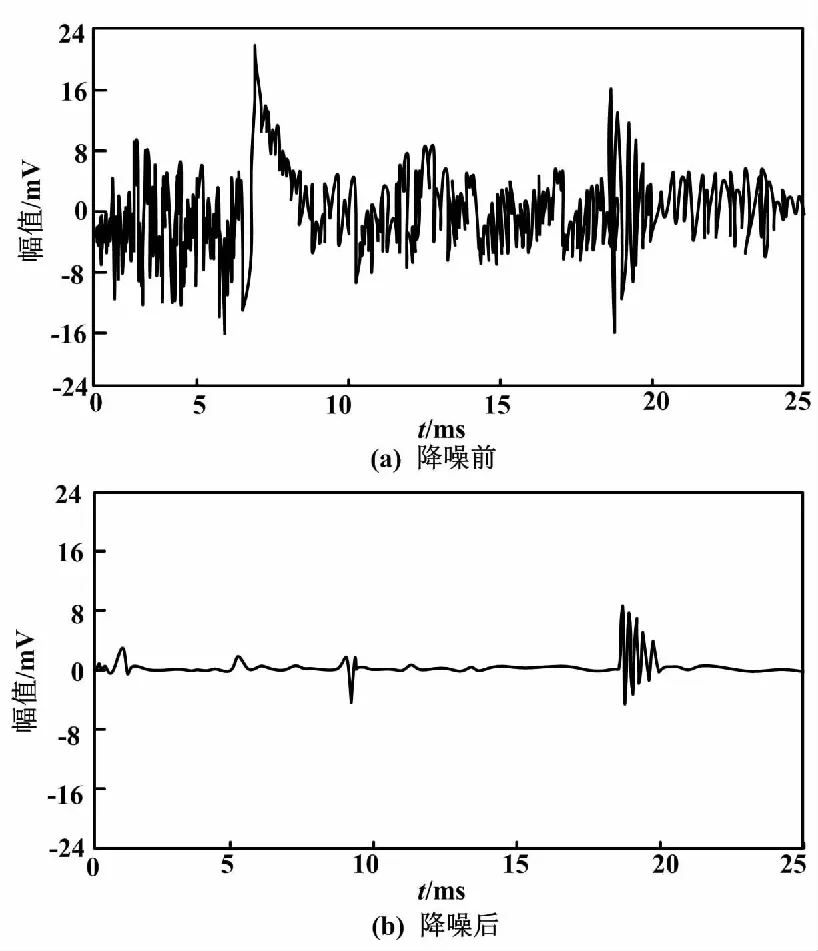
图3 气隙信号降噪前后的测试结果

悬浮信号降噪前后的测试结果如图4所示。

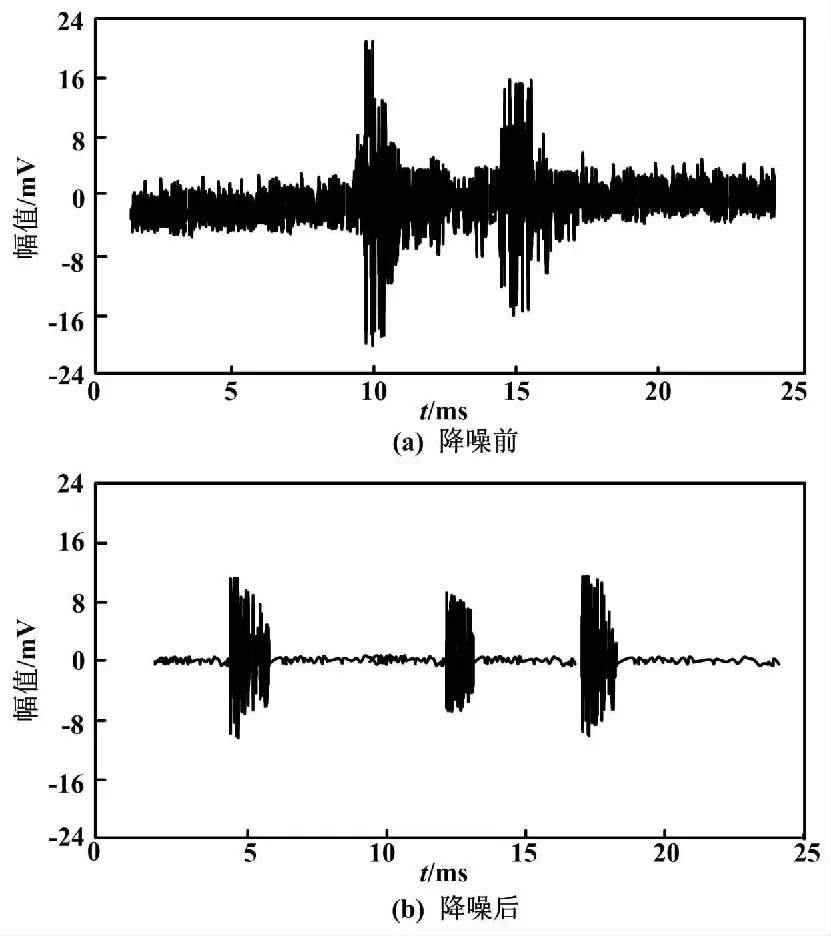
图4 悬浮信号降噪前后的测试结果

根据图3和图4的测试结果可知：本文方法具备良好的降噪效果，能够完成包含不同PD类别的信号降噪，降噪后的信号噪声极大程度地消失，可保证PD信号的可靠性。本文方法主要可确定噪声能量阈值，并依据该阈值对局部放电信号中有效信号和噪声信号进行调整，修正两者的比例以完成降噪，因此降噪效果良好。

为进一步测试本文方法的降噪效果，以信噪比(signal-to noise ratio,SNR)和波形相似系数λNCC作为评价指标，获取本文方法在不同噪声下的SNR和λNCC结果。2个指标的测试结果如图5所示。

图5 2个指标的测试结果

其中，SNR的值越高表示降噪效果越好，信号中涵盖的噪声越少；λNCC的值越高表示降噪效果越好，降噪后的信号完整性越高。由图5可知，随着噪声的逐渐增加，2个指标均呈现稳定趋势，且波动幅度较小，两者值均在0.8以上。这表明本文方法的降噪效果良好，能够很大程度地保证降噪后信号的完整性。

为测试本文方法对PD的检测效果，采用本文方法对样本集中的PD信号实行分类识别。PD的分类识别测试结果如图6所示。

图6 PD的分类识别测试结果

由图6可知：本文方法能可靠识别样本中的4种不同的PD信号类别，完成不同类别的信号检测。为进一步测试本文方法的检测效果，以特异性和灵敏度作为衡量指标，测试本文方法在不同SNR的情况下特异性指标和灵敏度指标的变化情况。

检测效果测试结果如图7所示。其中：特异性值越低，分类效果越好；灵敏度越高，检测结果稳定性越高。

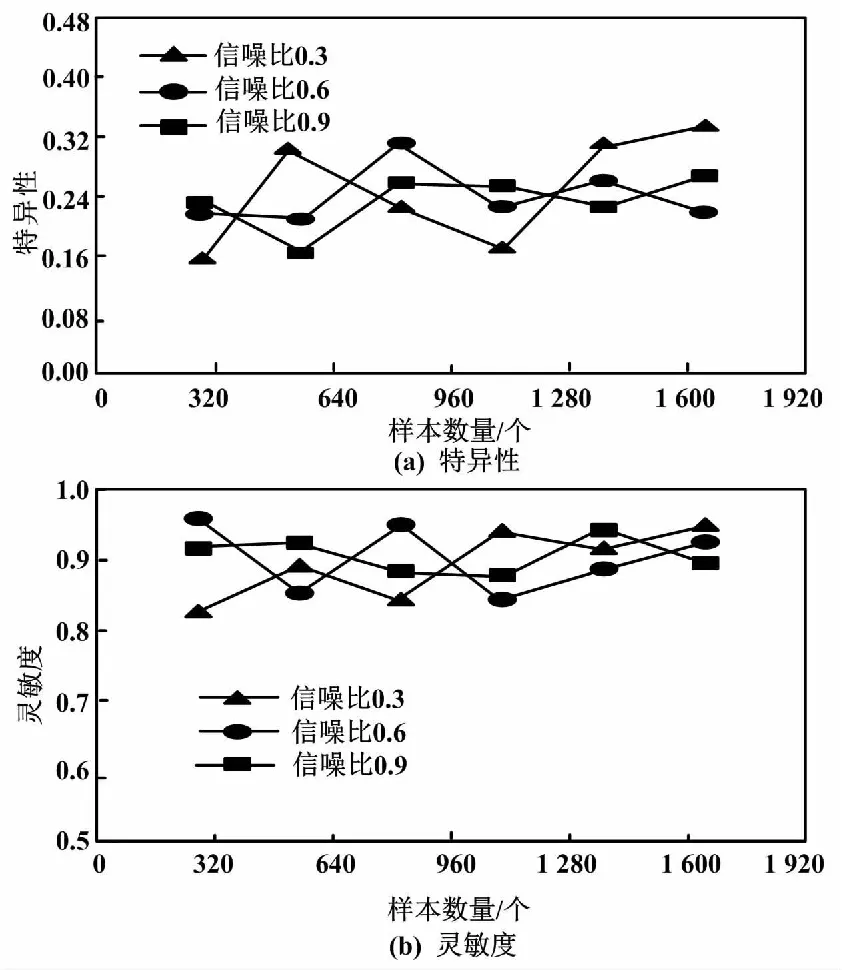
图7 检测效果测试结果

由图7可知，2个指标的期望标准为低于0.35和高于0.85。随着样本数量的增加，在不同的SNR时，本文方法的特异性和灵敏度良好，两者的值均满足期望标准。因此，该结果进一步表明了本文方法具备较佳的检测效果。

3 结论

随着现代科技的不断发展，人们对电能的使用需求逐渐提升。为保证人民生产及生活用电，需要重视电能输送电路的保护。高压电力电缆是众多工业企业、煤矿的主要电能输送线路。为保证电缆的安全性，需对PD实行检测。基于此，本文提出WT和SVM相结合的高压电力电缆PD检测方法。经测试，该方法可有效降低PD信号中的噪声，保证了降噪后信号的完整性，实现了精准识别。