采矿试验船简化结构设计方法

李成君，周佳

(中国船舶及海洋工程设计研究院 海工部，上海 200011)

由于面向深海的采矿船缺少实船数据及规范文件，需要针对采矿船进行总强度校核，确保结构设计可行性。采矿船外形为船型，船中具有月池，同时采矿船在月池区域集中布置塔架及钻采设备共1 600 t，使得无论是重载出港还是轻载到港，全船始终处于中垂状态，因此采矿船的设计波的控制载荷与常规船型有较大不同。为此，以深海采矿试验船为对象进行波浪载荷简化预报分析，计算波浪载荷，结合采矿船的特点进行总强度分析，确认结构设计关键位置。

1 波浪载荷简化预报

对波浪载荷预报的简化主要工作在于月池结构模型及全船重量重心调整2项工作。为了准确把握全船重量重心及月池结构对波浪载荷响应幅值的影响，对波浪载荷结果的差异进行分析。

由于船中有月池开口，角隅处易产生应力集中。在预报波浪载荷时，选取垂向剪力、弯矩以及船中转矩作为典型设计工况。

1.1 月池结构的影响分析

月池区域的控制载荷为垂向弯矩。在月池开孔范围内，垂向剪力和垂向弯矩随着月池尺寸的增加而有所减小，但变化较小。对于具有甲板大开口的船舶，其转转对变形的影响不容忽视。为了确定月池在波浪载荷预报中是否可以直接简化，建立水动力模型，见图1。

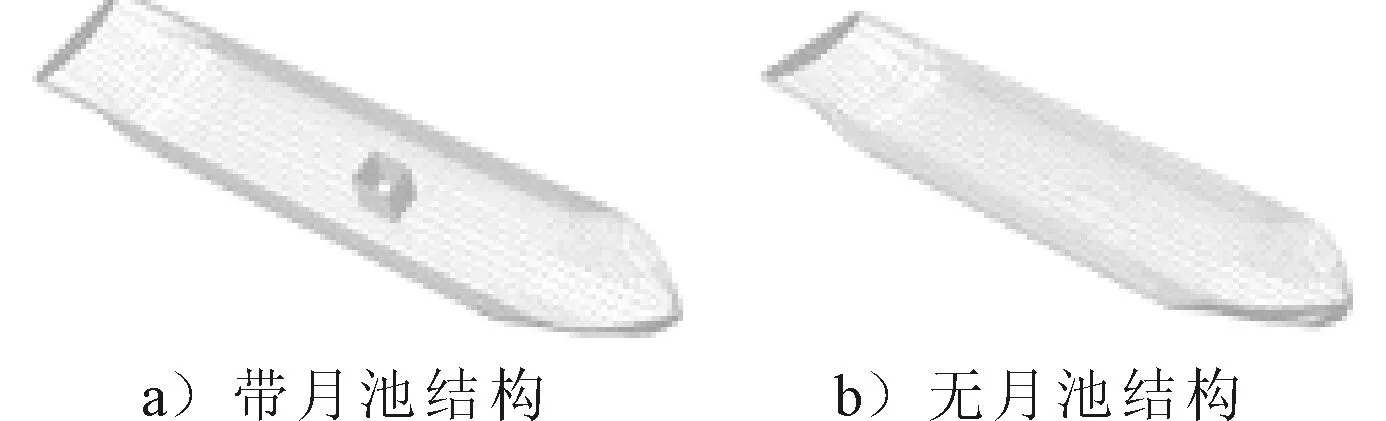
图1 不同模型湿表面网格

从定性角度分析，由于波浪载荷预报采用切片法，而月池结构改变了波浪诱导载荷的积分面积，特别是位于典型位置船中区域切片积分面积会降低，造成波浪诱导载荷差异，结果见图2。

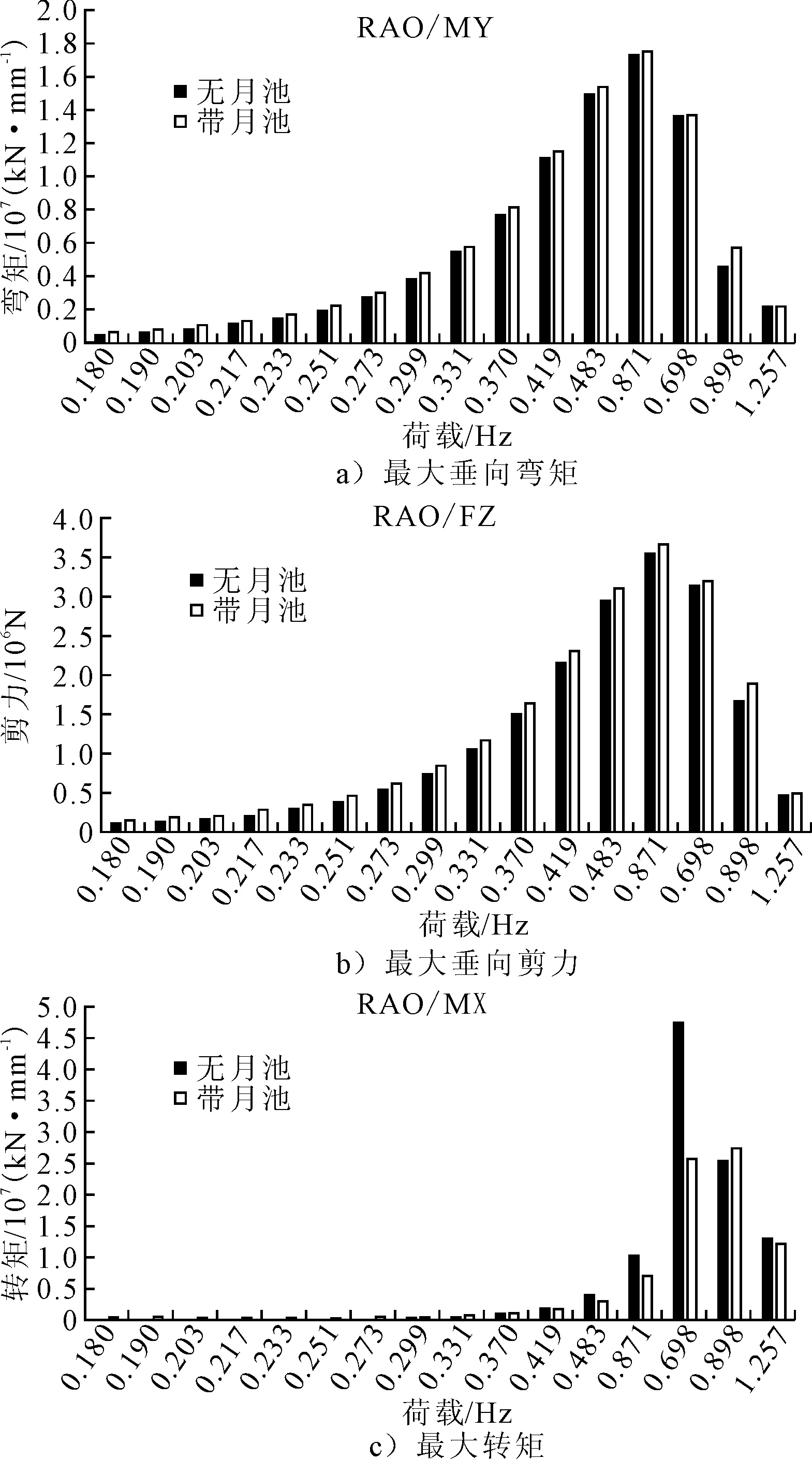
图2 月池结构对波浪载荷响应幅值影响结果对比

从图2可知，月池结构对垂向载荷影响较小，对转矩影响较大。月池区域由于距离最大垂向剪力位置较远，因此影响较小，分析船体梁载荷式(1)～(3)发现，垂向弯矩为沿船长方向的切片的垂向剪力的积分，因此最大垂向弯矩影响也不大，但是转矩仅依靠横剖面载荷进行积分，因此最大转矩受到月池结构的影响较大。

1)垂向剪力。

(1)

2)垂向弯矩。

(2)

3)转矩。

(3)

式中:为计算位置；为切片；，分别为刚体惯性力及力矩。

1.2 全船重量重心影响分析

船舶设计手册要求用于水动力分析的模型与真实船体的重量重心误差不得超过1%。由于重心的垂向坐标较难控制，因此简化调整重心垂向位置进行波浪载荷预报，意义重大。通过调整有限元模型材料密度的方式，选取重量重心变化范围较显著的3个模型进行比较。见表1。

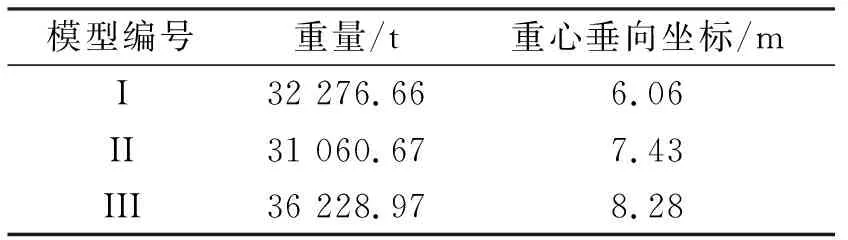
表1 不同质量模型重量与重心

提取靠近峰值的频率的预报结果，得到的幅值响应见图3，对比见图4。

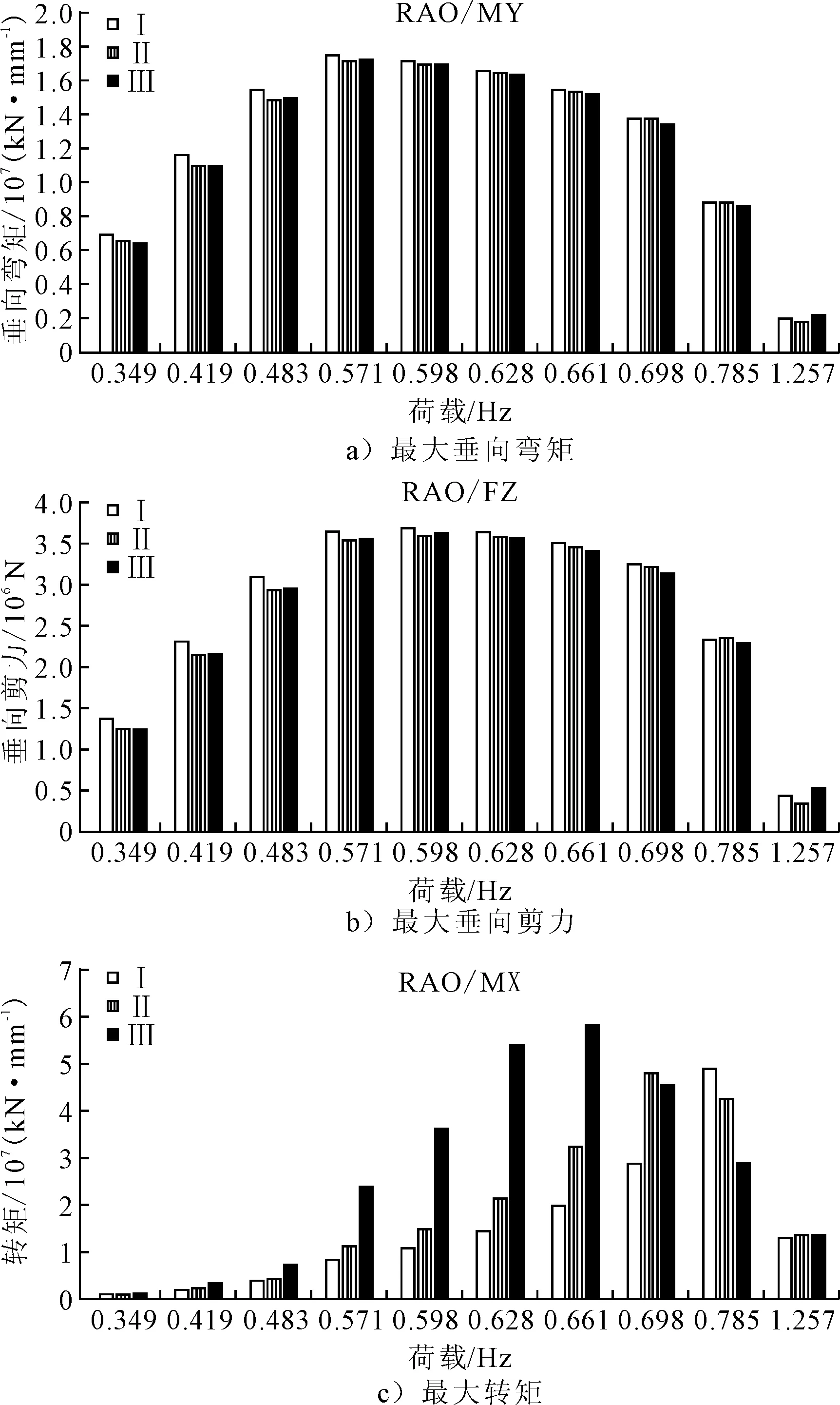
图3 重量重心对波浪载荷响应幅值影响对比

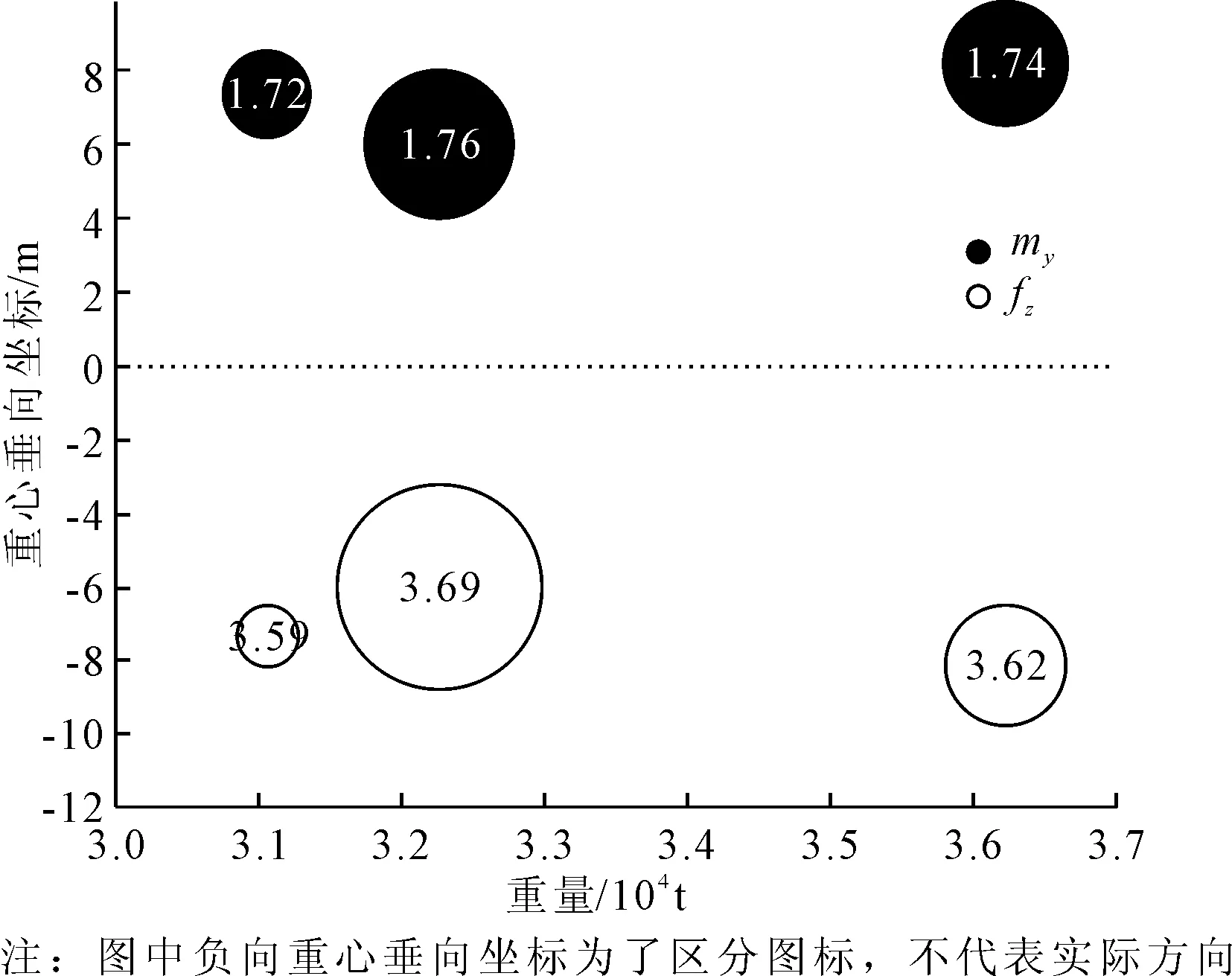
图4 重量重心对最大垂向弯矩及剪力的影响对比

由图3可见，最大垂向弯矩及剪力受到模型重量重心的微弱影响，不过随频率变化趋势一致，同时，最大响应幅值对应的频率不受模型重量重心误差的影响；而响应的最大转矩幅值则受到重量重心影响较大，另外最大转矩对应的波浪频率也不一样。

由图4可见，当模型重量偏大，或重心的垂向位置偏低，则对应的垂向弯矩及剪力的幅值偏大；当模型重量偏大，或者重心偏高，最大转矩的响应幅值偏大，最大转矩对应的波浪频率偏低。

1.3 波浪载荷简化预报方法小结

在兼顾效率及精度的条件下，当仅预报垂向载荷作为控制载荷的设计波预报时，忽略月池结构直接建立完整的湿表面模型计算，且适当放宽模型的重量重心准确度。当船体总强度处于临界状态，或者需考虑最大转矩作为控制载荷的设计波预报，则模型的月池结构及全船重量重心均应当按照规范要求进行准确模拟。

采矿试验母船的设计工况包括转矩，因此采用准确的湿表面及重量重心的水动力模型进行波浪载荷预报。

2 结构强度计算

以SESAM软件计算包为例，一般进行结构强度计算的流程见图5、6。

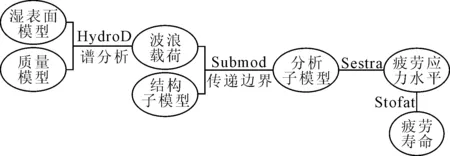
图5 结构总强度及局部强度分析流程

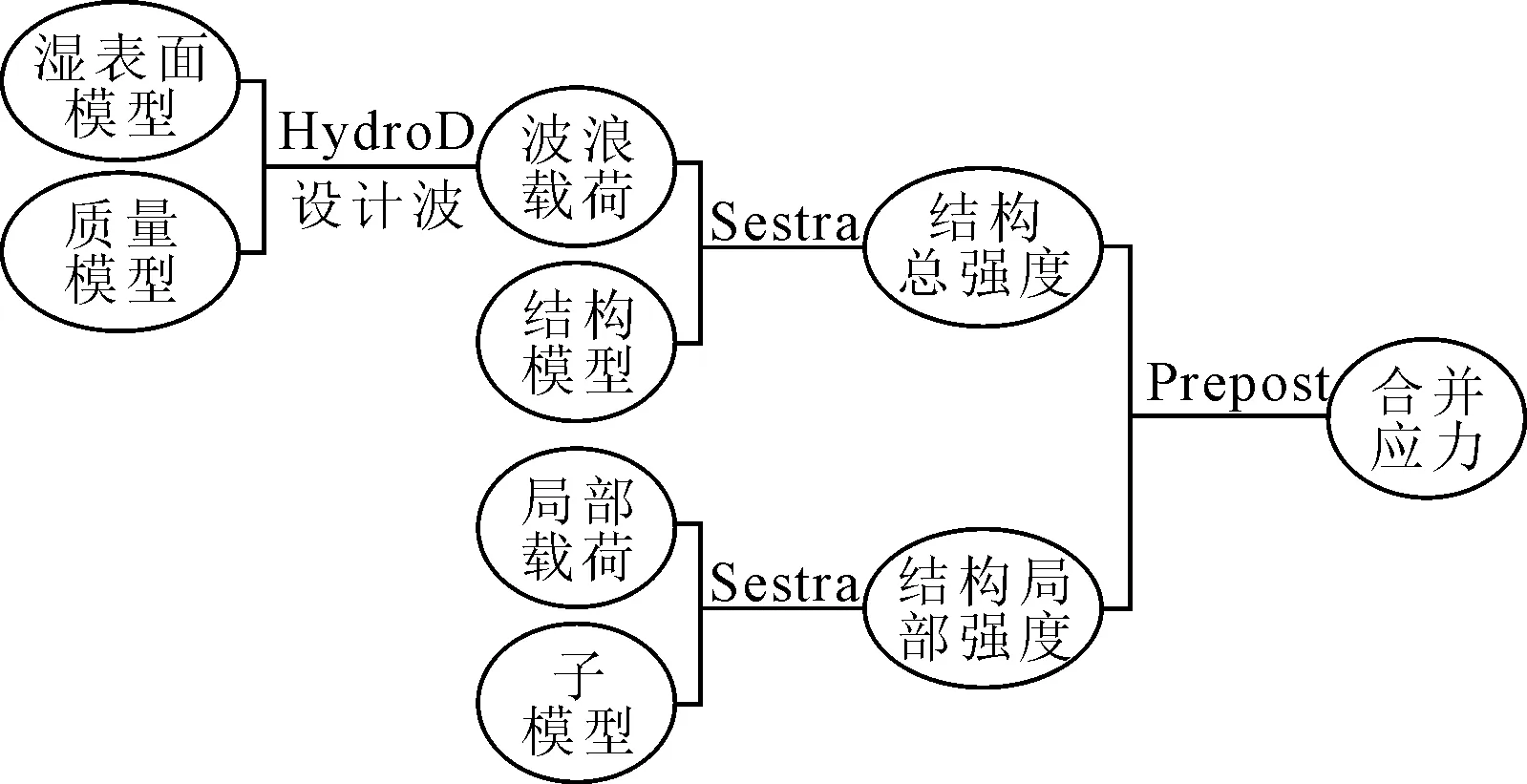
图6 结构疲劳强度分析流程

2.1 总强度计算

全船结构有限元模型及质量模型共用一个模型，见图7。针对有限元模型进行简化，由于最大剪力一般位于1/4～3/4船长位置，因此在1/5～4/5船长范围内按照肋距以及纵骨间距的常规网格进行建模，对于该范围之外的模型采用强框间距作为单元尺寸进行建模。

图7 全船有限元模型&质量模型

计算工况选取6级海况，选取所有工况的包络载荷进行计算，将装载工况简化为航行出港，航行到港，得到的设计波参数见表2。

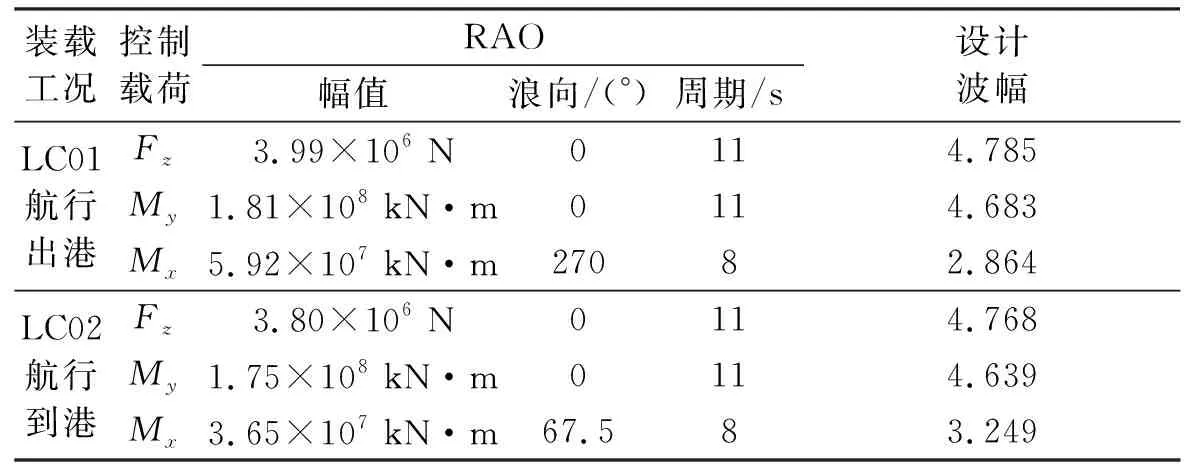
表2 不同质量模型重量与重心

根据表2中的设计波进行总强度计算，选择典型部位的计算结果见表3，应力见图8。

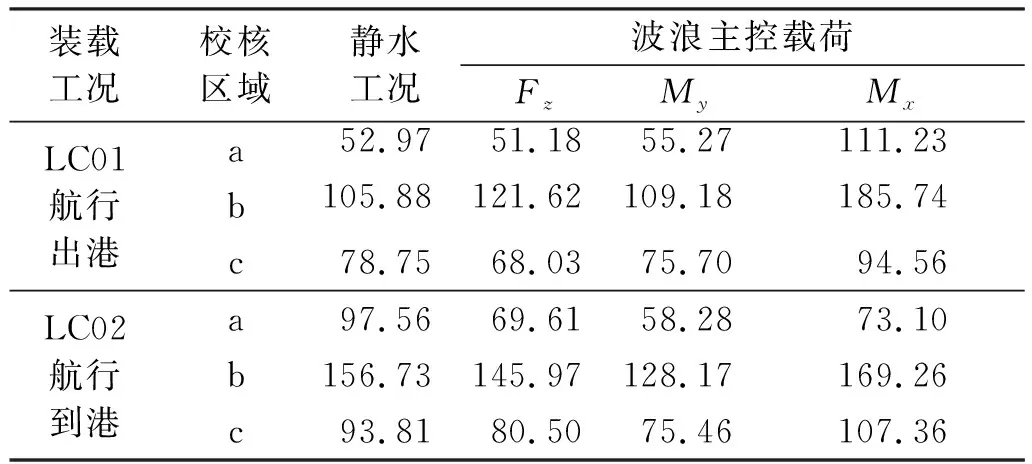
表3 全船总强度典型部位应力计算结果 MPa

图8 典型部位应力云图

从图8及表3可以看出，最大应力发生在纵舱壁位置，其次是主甲板，最后是外壳，因此可以判定应力传递路径为从塔架到纵舱壁，到甲板再到外板，在进行结构加强设计时根据应力传递路径简化月池区域的结构加强，由于应力在传递过程中存在结构刚度的抵抗，应力水平将会逐级衰减，根据应力传递路径逐渐降低结构刚度，可避免整体加强造成的结构冗余，还能避免加强区域偏差导致的应力集中。

2.2 局部结构强度计算

由于总强度采用梁单元模拟塔架，而应力无法从梁单元传递到板单元，因此塔架局部结构强度的计算并不准确。采用子模型法对塔架底座及月池角隅的局部结构强度进行分析。根据总强度分析的粗网格计算结果，截取对应区域的模型细化，见图9。

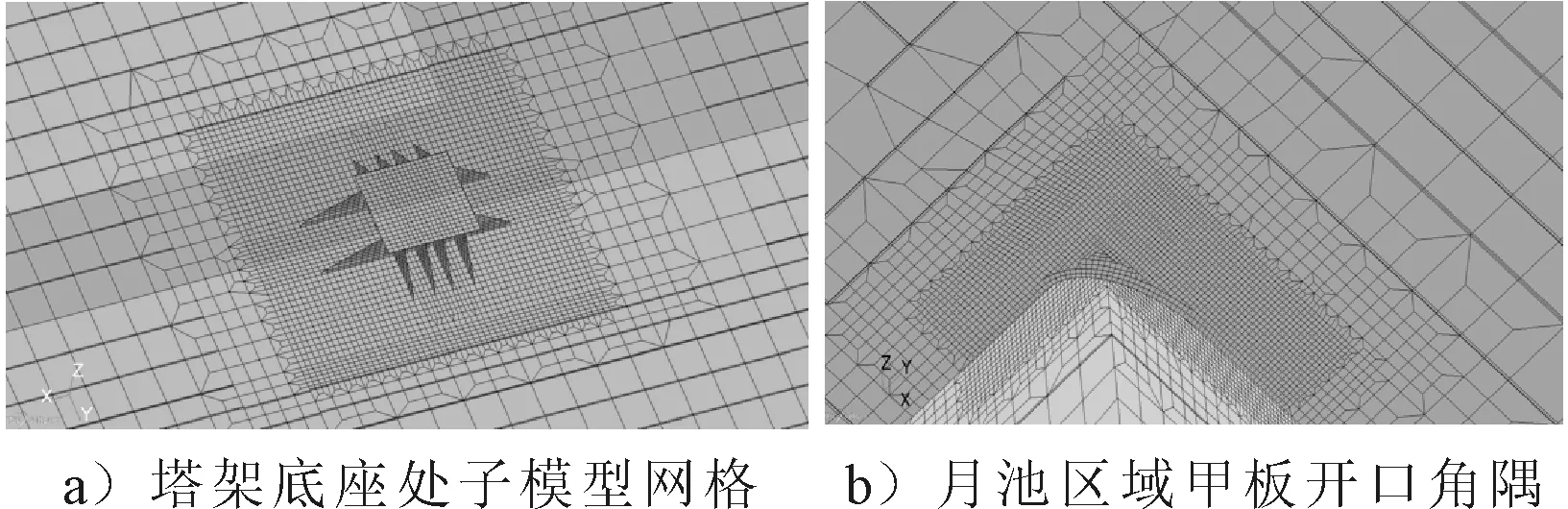
图9 子模型网格划分

选取与船体变形方向一致的局部载荷作为典型载荷计算疲劳寿命。

2.3 疲劳寿命计算

疲劳环境选取全球海况，波浪谱选为PM谱，计算流程同前。

该船用于校核疲劳的节点主要是塔架底座，主甲板及船底月池开口角隅。直接从局部强度模型中提取模型并继承局部模型的边界条件，疲劳校核模型及边界条件见图10，塔架底座模型单元总数14 672，月池区域开口角隅模型单元总数14 335。

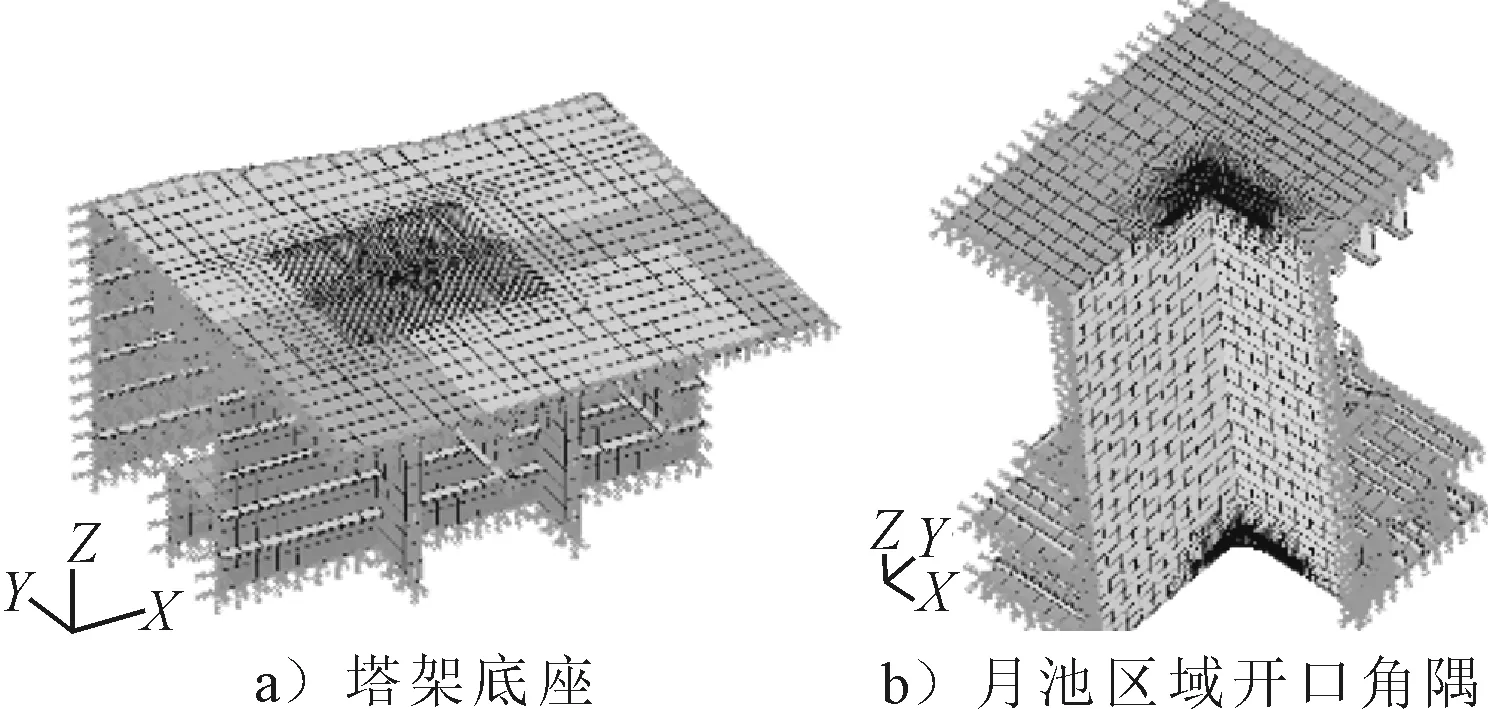
图10 疲劳校核模型

一般疲劳分析需要根据不同装载工况及作业场景进行概率分布计算。在工程设计过程中，可根据情况进行简化，提取危险场景进行估算。限于篇幅，选取某热点位置以及插值方式进行疲劳校核，热点位置见图11、12。

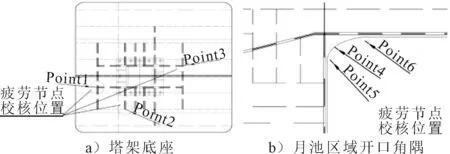
图11 疲劳校核热点位置

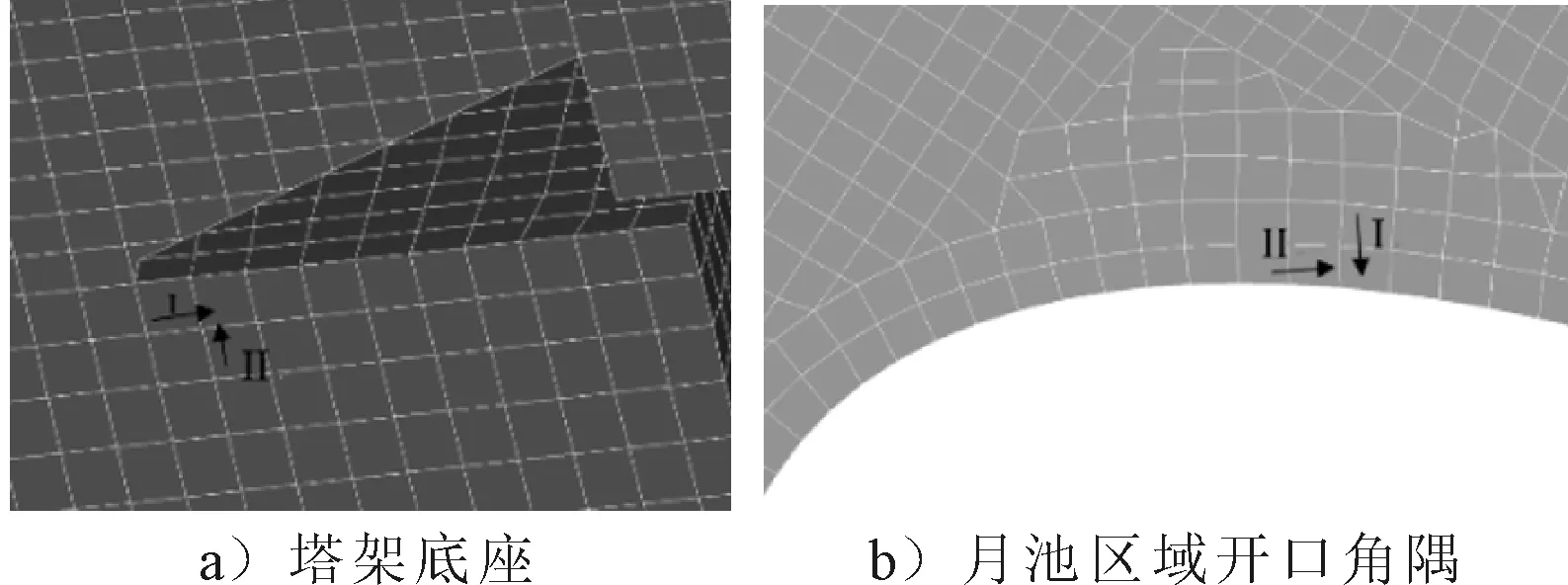
图12 疲劳校核插值方式

采用谱分析方法进行全概率疲劳寿命计算，需要选择正确的-曲线，塔架底座由于是焊接结构，其疲劳性能较差，选取曲线，月池开口区域选取曲线。对热点疲劳寿命进行计算，选取典型插值结果见表4。

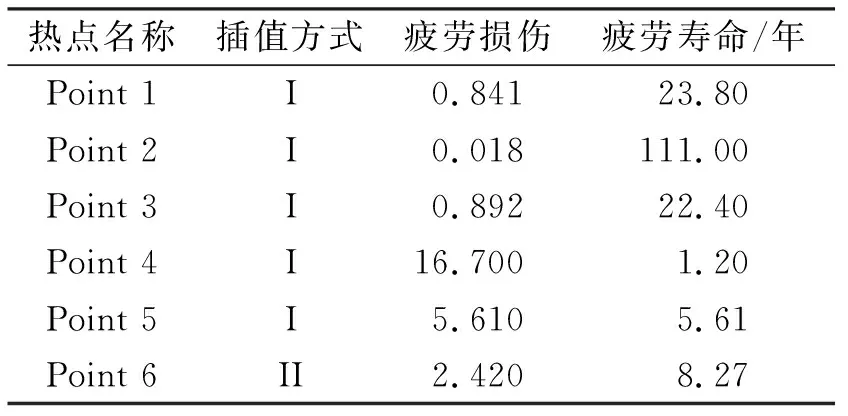
表4 热点疲劳计算结果

可以看出最短的疲劳寿命为1.2年，位于主甲板月池开口角隅位置。考虑到本船功能定位于海上采矿试验，并非正式服役，因此目前的疲劳结果可以满足试验要求，不过本船若作为采矿作业条件时，该处是一个危险点，在设计过程中应当进行加强。

2.4 强度校核简化方法小结

该船简化工作主要包括在简化设计载荷的过程中考虑船体变形与局部载荷叠加的影响；计算模型选择子模型方法进行强度分析；将关注区域的网格按照受力特征进行网格细化，然后将全船模型的边界条件传递到子模型中；另外，根据应力传递路径，简化局部结构加强。

3 结论

针对采矿试验船得出简化模型的可行性方法：当主控载荷为垂向载荷以及总强度非临界状态的前提下，模型可简化处理，当需要考虑横向载荷作用时则不可简化处理。

采用子模型法对月池区域结构屈服及疲劳强度进行分析，给出了基于子模型分析的流程以及方法，确定强度分析中的应力传递路径，为结构设计以及强度评估提供技术支持，并为后续的局部结构加强提供参考。

但是，分析的完整性存在不足，主要在于模型简化方面，只定性给出月池结构及全船重量重心对波浪载荷幅值影响，没有针对不同船型的结果的影响进行对比，并获取估算公式，为模型简化工作提供数据支持。后续应考虑选取不同的成熟船型进行对比分析，计算出月池结构或者重量重心对不同载荷的影响因子，得到适应性较好的载荷估算公式，然后采用新船型进行验证，从而更准确地把握处理简化模型的波浪载荷的预报方法。