船舶爬壁机器人电磁吸附设计分析
2022-10-28韩力春王黎明闫晓玲
韩力春,王黎明,闫晓玲
(海军工程大学 电气学院控制工程教研室,武汉 430033)
船舶爬壁机器人与陆地机器人的不同之处在于其兼具移动和吸附功能,能够于倾斜的船舶壁面上完成爬壁运动,通过配备除锈、清洗、焊接所需的高压水枪、焊枪等装置完成对应作业任务等,每种作业任务对吸附力的要求不同。此外,作业环境的船舶壁面并非平滑不变,往往存在水藻和铁渣等障碍物的,这导致爬壁机器人与壁面的间距并非一成不变,对机器人的越障能力有一定要求。从移动方式来看,一般,履带爬壁机器人比轮式的越障能力强;从吸附方式来看,多采用永磁吸附、负压吸附和正压吸附等。但这些吸附方式一般不可调节吸附力大小,难以使爬壁机器人应对存在障碍物的船舶壁面和不同的作业需求。为此,考虑采用电磁吸附爬壁机器人,设计新式电磁吸附装置,对机器人进行力学分析,根据得到的最小吸附力条件设计电磁铁结构。通过建立电磁铁和永磁铁有限元仿真模型,模拟船舶壁面与机器人的间距,验证此电磁铁的吸附能力,实现吸附力可调。
1 电磁吸附单元设计
1.1 爬壁机器人结构设计
结合船舶爬壁机器人作业环境,用SolidWorks三维设计软件建立爬壁机器人整机结构见图1。移动机构主要由履带和带轮等组成,吸附机构主要由滑轨和电磁铁等组成,驱动机构主要由步进电机和行星减速器等组成,车体框架结构采用H形架构,电源、控制器、电机驱动模块等安装在车体框架上。电磁铁等间距镶嵌在履带中,因此电磁铁既是吸附机构,也是移动机构的一部分,机器人通过步进电机带动带轮和履带使其移动于壁面之上,同时,通过与壁面接触的部分电磁铁产生吸附力吸附于壁面之上。
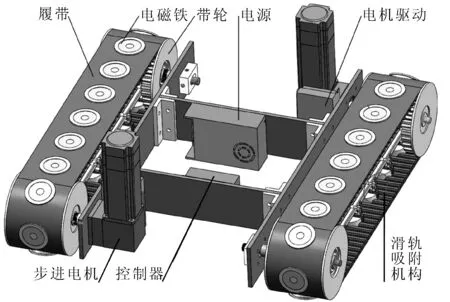
图1 爬壁机器人整机结构图
1.2 机器人最小磁力条件分析
运行于船舶,涉及到物体坐标系和惯性坐标系,需建立海面上的惯性坐标系-,以及船舶和爬壁机器人的物体坐标系-、′-′′′,如图2所示,为船舶壁面倾角,范围是0°~90°;为爬壁机器人姿态倾角,即机器人在′′轴与轴的夹角;平面为船舶壁面;′轴与平面的法向量方向一致。

图2 坐标关系变换
结合文献[12-13]和爬壁机器人在船舶壁面爬壁过程中的实际运行情况可知,临界状态主要包括沿船舶壁面下滑、平行于竖直方向的纵向倾覆、垂直于竖直方向的横向倾覆、沿壁面法向方向掉落等几种状态,针对电磁铁设计而言,需取临界状态中最小磁力条件中的最大者,即纵向倾覆力作为电磁铁设计的最小磁力条件。
爬壁机器人会出现纵向倾覆是因为机器人本身的自身重力会产生倾覆力矩,力矩主要包括倾覆力矩与抗倾覆力矩,倾覆力矩会导致机器人倾覆,由重力分别在′′轴和′′轴上的分量乘以对应的力臂而来;抗倾覆力矩会阻止倾覆发生,由吸附力和摩擦力分别乘以对应的力臂而来。当倾角变化到一定程度,致使顶端电磁铁与表面相接触的B点处所受的支持力为零,B点处的摩擦力为0,进而倾覆力矩大于抗倾覆力矩,因为履带为柔性体,所以由顶端电磁铁开始,由B至A点的电磁铁依次脱落,发生纵向倾覆,此时受力情况见图3。
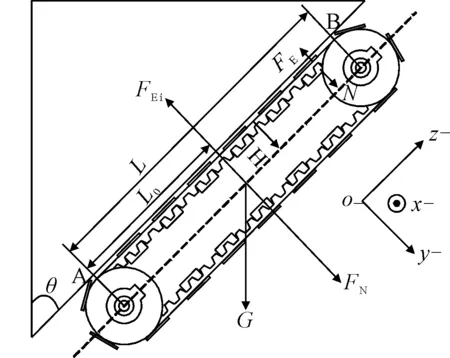
图3 纵向倾覆力学分析
1)倾覆力矩。

(1)
2)抗倾覆力矩。
=·
(2)
3)纵向倾覆临界条件。
≥
(3)
=2
(4)
式中:A、B点分别为机器人底端、顶端与壁面的接触点;为机器人重心到船舶壁面的距离;为A、B 2点间距离;为单部电磁铁的电磁力。
联合式(1)~(4)得出:为使机器人不发生平行于竖直方向的纵向倾覆,单部电磁铁的最小电磁吸附力所需要满足的条件为
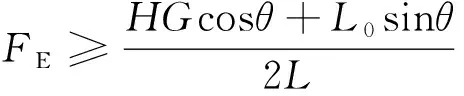
(5)
代入机器人参数,通过数值分析得到纵向倾覆力见图4。由图4可知,在=74°时取得极值,为178.19 N。

图4 纵向倾覆力随倾角的变化
1.3 电磁铁设计
所选用的是直流吸盘式电磁铁,电磁铁为E型结构。经过经验公式求此圆形电磁铁线圈的匝数、线圈厚度、线圈高度,线圈厚度即为环形线圈的内外径之差,线圈高度与厚度决定了电磁铁外围Q235钢的半径尺寸。
为保证安全吸附以及计算方便,要对最小吸附力留有一定裕度空间,将其值取为180 N。最终得到电磁铁的结构设计参数为电磁铁环形线圈内、外径为30、10 mm,电磁铁高22 mm,通过SolidWorks软件设计的电磁铁三维模型见图5。

图5 电磁铁三维模型
2 电磁场数学模型分析
电磁铁的场模型涉及到电场与磁场两部分,其磁感线要穿过电磁铁、空气、船舶壁面等最少三种介质,一般用Maxwell方程组进行描述场模型,采用基于Maxwell方程组原理的COMSOL软件的电磁学模块进行仿真分析,然后用应力张量法推算出电磁力公式。Maxwell方程组的积分形式为
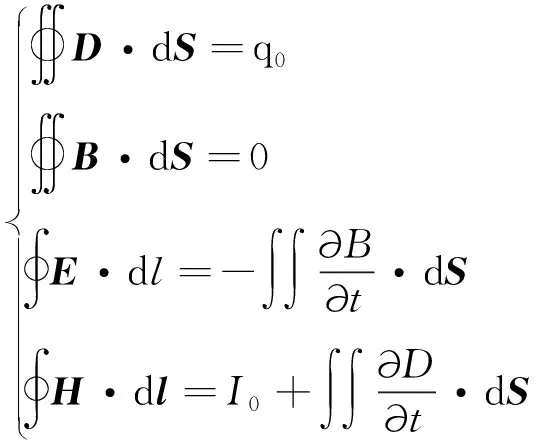
(6)
式中:为电场强度;为磁感应强度(T);为电位移矢量;为磁场强度,A/m;为电磁铁与空气的闭合面。
此方程组从上至下依次对应静电场的高斯定理、磁通连续性定理、法拉第电磁感应定律、安培定律,对应的原理图见图6。
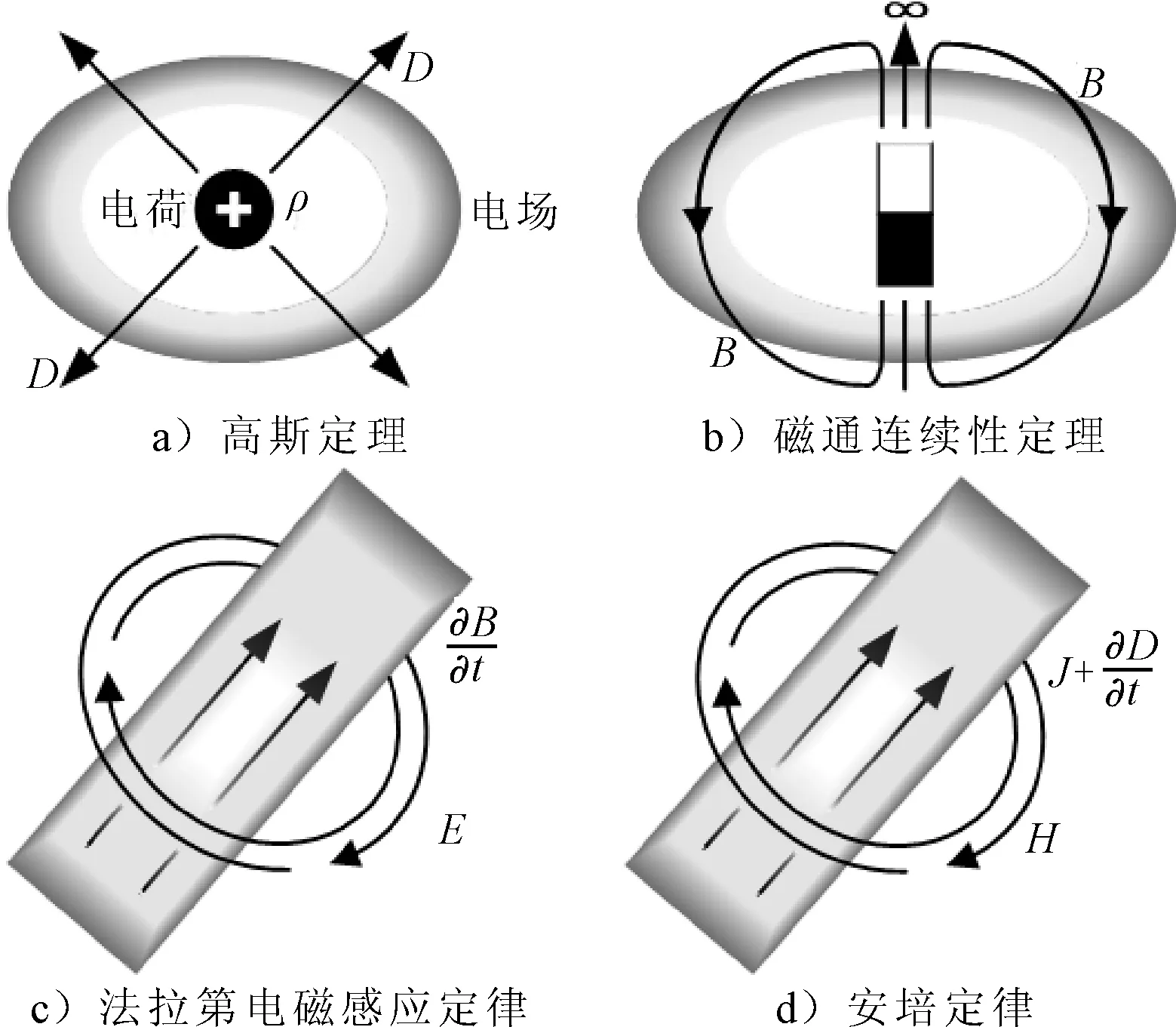
图6 Maxwell方程组原理示意
在均匀各向同性介质中,本构关系如下。

(7)
式中:ε为媒质的介质常数;μ为媒质的磁导率;σ为媒质的电导率;为电流密度,A/m。
在非均匀介质中,还要考虑电磁场量在界面上的边值关系。为使磁场计算简单,引入磁标势的关系式为

(8)
根据式(7)的本构关系,考虑其中磁场与剩余磁通密度之间的本构关系,将约掉,即
=+
(9)

联合式(6)、(8)、(9),推导出磁标势为

(10)
、、为已知,因此可通过式(10)和边界条件求解,那么再联合(8)、(9)就可以求出,为了达到更好的仿真效果,在有限元分析时,有限元模型边界的尺寸将大于电磁铁模型。
根据Maxwell应力张量法,得到电磁力 (即电磁场的应力)的定义式为

(11)
式中:为电磁张力应量。
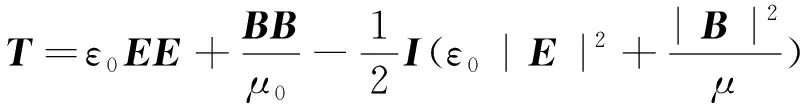
(12)
式中:为单位张量;为真空介电常数;、为、与其自身的并矢张量。
联合式(11) 、(12)得到电磁力为

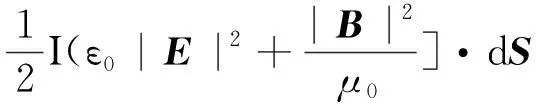
(13)
3 有限元分析
COMSOL软件电磁学模块的分析基础是Maxwell方程组,COMSOL软件内置Maxwell方程组的形式为亥姆霍兹方程,其是一定频率下电磁波的基本方程,其解()代表电磁波场强在空间中的分布,每一种可能的形式称为一种波模。
其稳态时,方程为

(14)
瞬态分析时,方程为
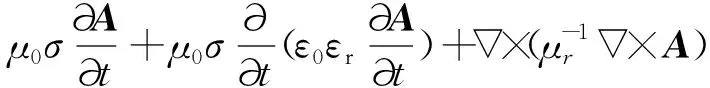
(15)
式中:为相对介电常数,是复数,可用虚部代表介质损耗;为磁矢量势;为角频率。
针对永磁铁和电磁铁这两种不同的模型,分析中采用对应的物理接口,相应的控制方程采用对应的数学方程描述,简化模型,去掉不必要的约束变量,用边界条件方程来约束。
3.1 永磁体有限元仿真分析
永磁铁仿真时,模型中无电流,只考虑磁场作用,此时磁通量守恒为其控制方程依据,磁绝缘(即磁场线与边界平行)为其边界条件,分别为
1)控制方程。

(16)
2)边界条件。
·=0
(17)
式中:为磁体的法向量,乘积为零说明磁场线垂直于此法向量。
根据此前最小电磁力分析得到的磁铁尺寸,建立永磁体有限元分析模型并导入,采用“磁场,无电流”这一物理场模块,导入后永磁铁和铁板对象名称为imp1。加入立方体空气ext1将永磁铁和铁板完全包围,通过布尔操作ext1+(imp1×ext1)使空气充满此立方体。并加载上述的控制方程和边界条件,永磁铁与壁面的间距为1 mm,船舶壁面采用100 mm×80 mm×20 mm的铁板代替,得到的磁通密度仿真剖图见图7a),永磁铁与壁面接触的磁通分布见图7b)。
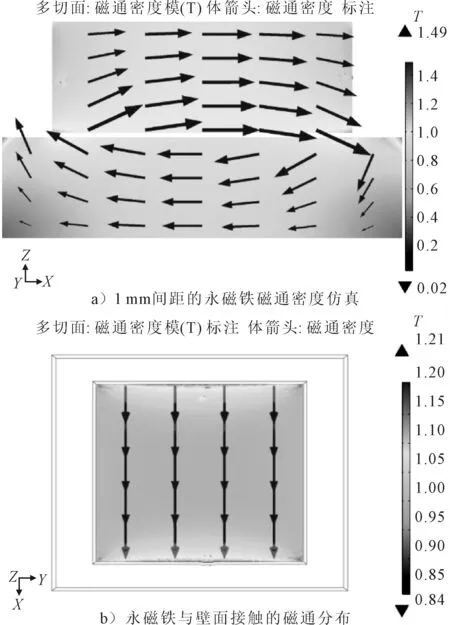
图7 永磁铁磁场有限元仿真模型
由图7可见,磁感线在磁铁内部是由S到N,外部则相反,符合实际磁感线方向,仿真正确,铁板距离永磁铁越近,系统密度越大、越密集,代表电磁力越大,此仿真下由COMSOL Multiphysics软件计算出的最大磁力大小为160.783 N,在铁板尺寸不变的情况下,以同样的网格密度划分、同样的空气空间,改变永磁铁与铁板间距离,以1 mm距离的等差梯度为自变量,进行1~10 mm间距的仿真,观察磁力的变化情况,为使磁力变化趋势更能贴合数据的变化走向,用MATLAB对所得数据进行拟合,见图8。
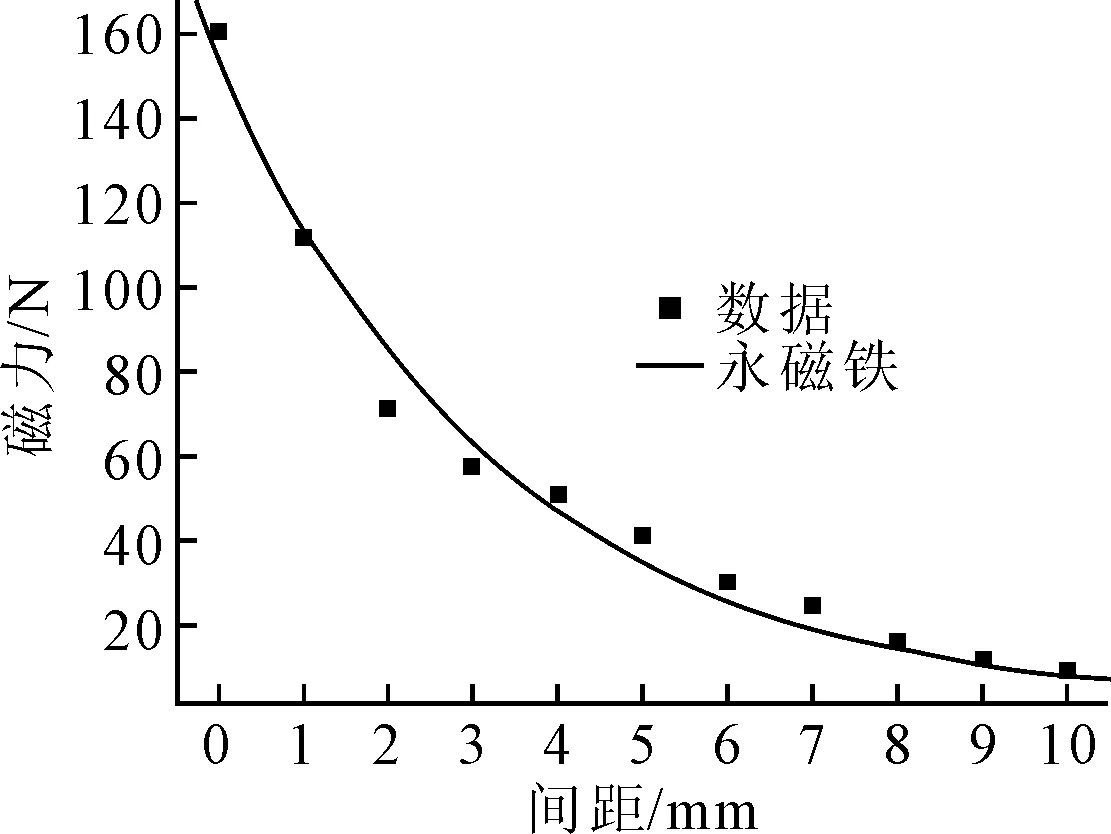
图8 永磁铁的磁力与间距关系的变化
由图8可见,磁力值随着永磁铁与壁面之间的间距的增大而变小,符合常识。间距在3 mm之前变化时电磁力减少幅度较大,磁力迅速减小,超过3 mm后电磁力变化幅度缓慢,但已经不满足最小吸附力条件。爬壁机器人行走于船舶壁面上时,难免会遇到凸起的铁锈和海藻等障碍,这时部分磁铁与船舶壁面之间就不再是贴合状态,而是短时出现上面曲线中不同的间距状态,那么在倾角不变的情况下机器人所需要的最小吸附力没变;但由于间距的改变而导致永磁铁提供的吸附力变小,不满足安全吸附条件,可是磁力又不可调,为此,引入电磁吸附以弥补磁力不可调的缺陷。
3.2 电磁体有限元仿真分析
电磁铁仿真时,根据其电磁铁吸附原理可知,仿真模型中通有电流,不仅要考虑磁场影响,还要考虑电场作用,此时控制方程依据内要加入安培定律,其边界条件改为考虑磁矢量势。
1)控制方程。

(18)
2)边界条件。
×=0
(19)
电磁铁是由线圈组成,线圈必须是闭合回路,4种不同类型的线圈见图9,各线圈特性如下。
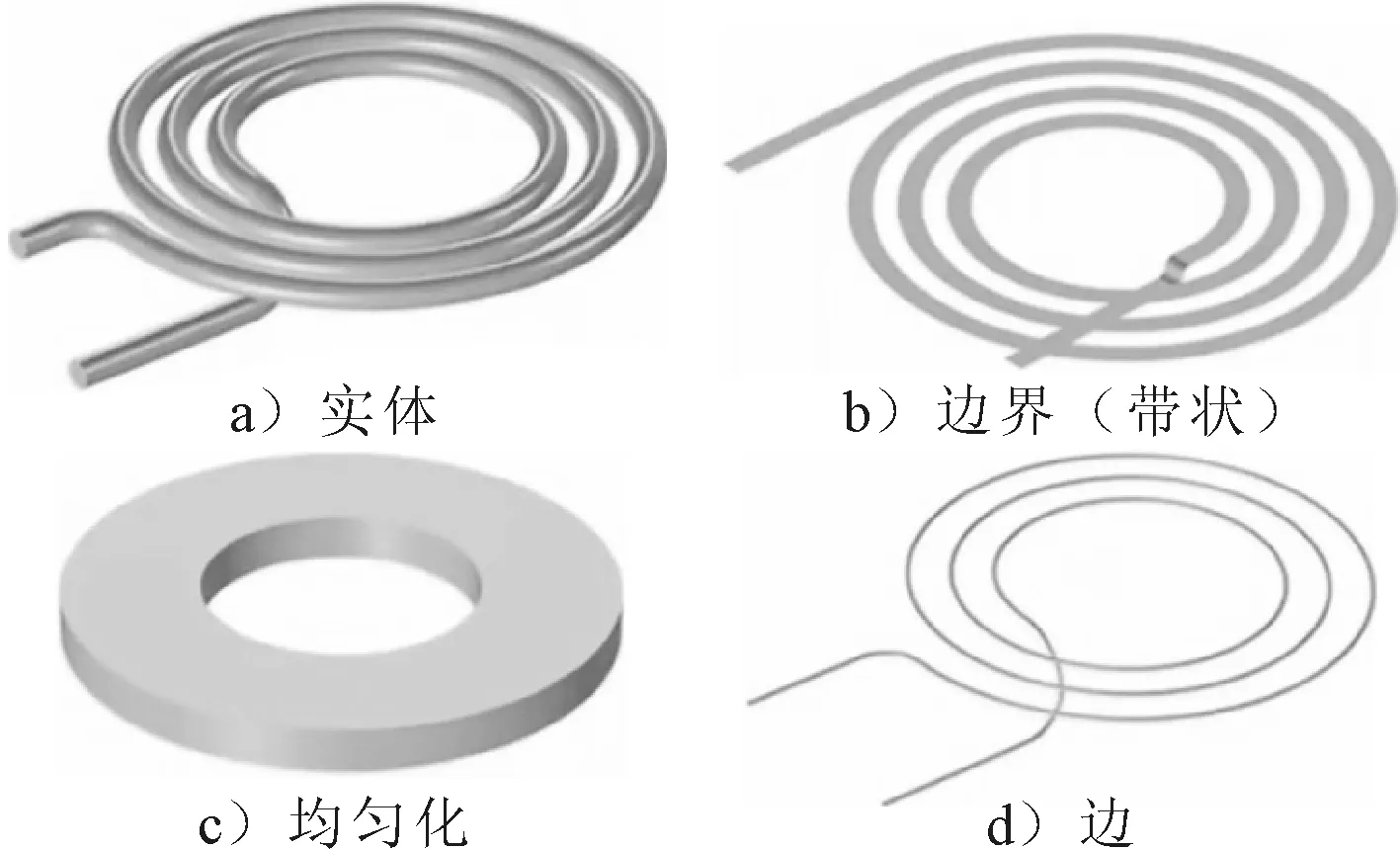
图9 线圈类别
1)图中的实体线圈未作任何近似处理,更能准确反映真实情况,但是在进行仿真运算时候要考虑很多的线圈的匝间影响,运算效率低。
2)边界线圈特征近似描述不考虑厚度影响情况,以简化网络,不考虑上下方向的变化。
3)均匀化线圈是忽略匝间的相关影响的近似描述,忽略线圈电容近邻谐振效应。因为电磁铁所通的电流频率很低,属于低频电磁场,线圈的趋肤深度小,可以忽略,不影响电感分析。只看磁场和电磁力方面,并不影响电磁铁的仿真结果。
4)边线圈常用于激励场,查看磁通量大小,间接计算电感,但不能计算电阻和电容。
仿真模型采用均匀化线圈,用SolidWorks建立电磁体有限元分析模型,SolidWorks和COMSOL Multiphysics有联合接口——LiveLink for SOLIDWORKS,模型的变动可实时同步到COMSOL软件中。对于电磁铁有限元分析,要加入的物理场模块如下。
1)电路。所设计的电磁铁采用直流24 V电压源供电,此电路模块即用于模拟电源供电。
2)磁场和电场。产生磁场和电场,仿真中控制方程和边界条件的来源。
电磁体有限元分析得到的磁通密度见图10,面的剖面图和电磁铁与船舶壁面接触面的磁通分布见图11。
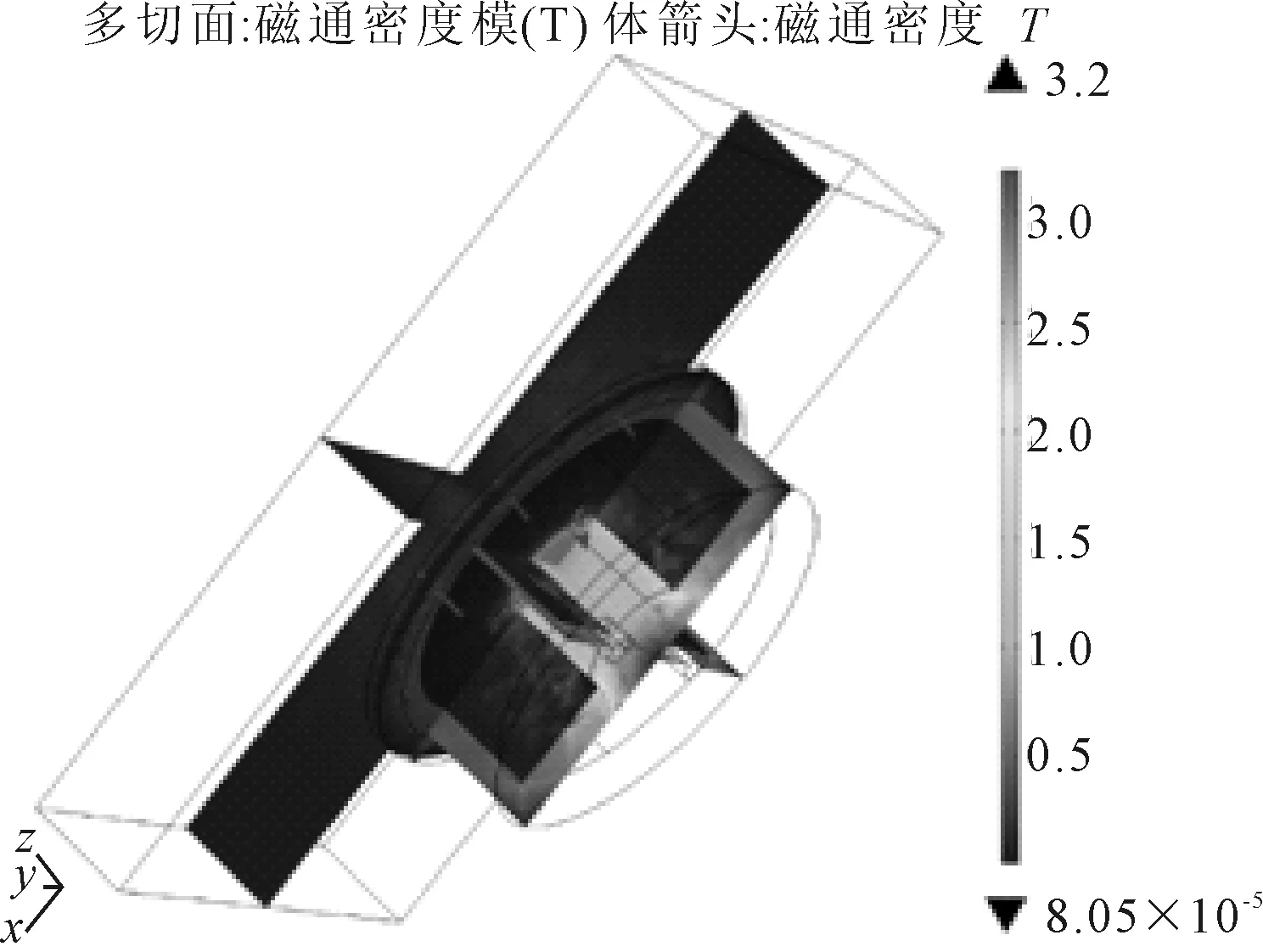
图10 电磁铁磁通密度三维视图

图11 电磁铁各位置的磁通分布图
从图11a)可见,电磁铁铁芯位置集中了主要磁通量,在铁板上产生的电磁力也最大,周围的磁通则较为稀疏,相应的电磁力也更小。总体对比图7a)和图11a)的磁通量,电磁铁的最大磁通量大于永磁铁,这是由于电场的存在;从面上对比图7b)和图11b),电磁铁与壁面接触时的接触面上的最大磁通量为1.38 T,永磁铁为1.21 T,因此,在适合机器人履带的条件下,电磁铁所能提供的最大吸附力稍大于永磁铁。
同样,在铁板尺寸不变的情况下,以同样的网格密度划分、同样的空气空间,电磁铁本身特性和电路内电流、电压是不变的,间距属于外在影响因素,改变电磁铁与铁板间距离,以1 mm距离的等差梯度为自变量,进行1~10 mm间距仿真,磁力变化情况见图12。
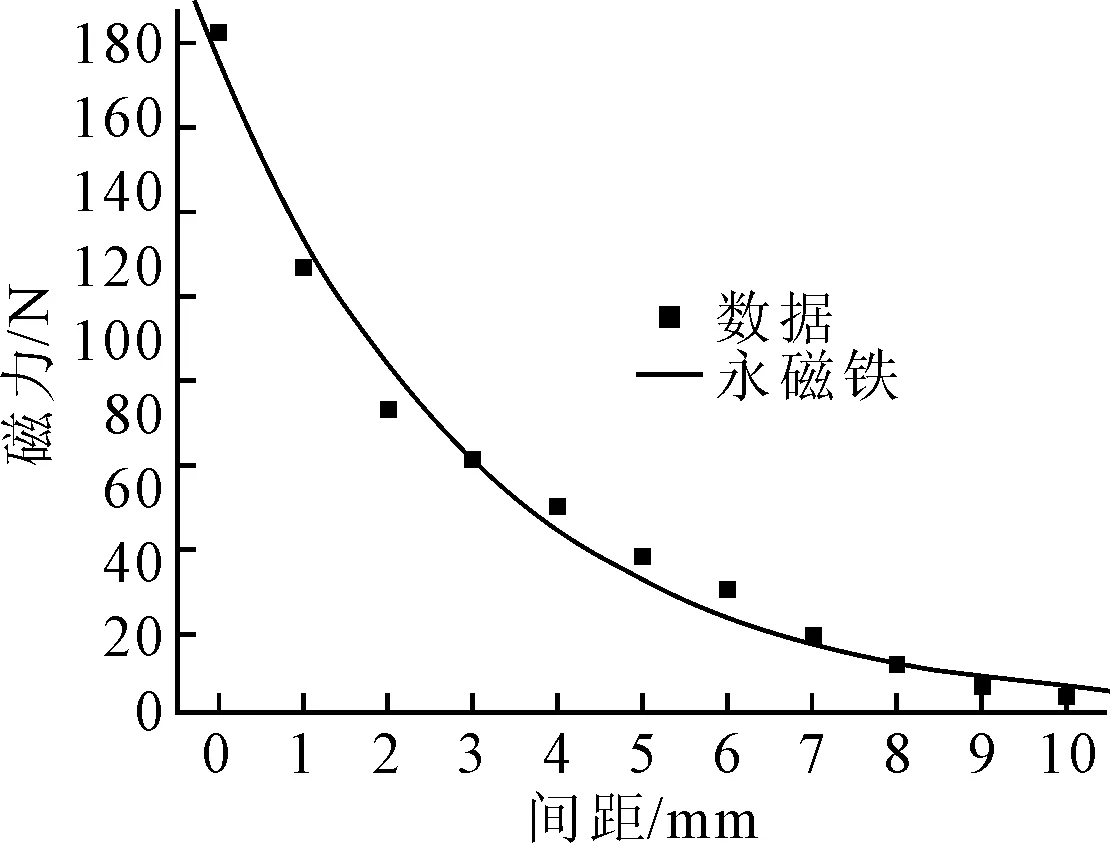
图12 电磁铁的磁力随间距的变化
由图12可见,在间距为0 mm时取得最大电磁力为182.93 N,间距从0~3 mm的前期阶段,电磁力迅速下降,与拟合指数趋势类似,后期磁力变化放缓,但磁力很小,不能满足要求,若磁力不足以使机器人吸附于壁面,可在现有的基础上适当增大电流以达到磁力要求,与图8对比,在同间距的情况下电磁铁可产生的吸附力较大,一定程度上提高了越障能力。
4 结论
1)纵向倾覆为机器人临界状态,电磁铁的最小磁力来源可由此作为依据,减小计算量。
2)建立电磁铁和永磁铁的有限元模型不同,控制方程和边界条件随之变化,电磁铁最终所产生的吸附力大较大,能够满足机器人的安全吸附要求。建模时可将空气的范围尽量扩大,以贴近实际。
3)应力张量法所建立的有限元仿真模型模拟了磁力-间距变化情况,电磁铁可以在安全吸附的前提下实现吸附力可调,电磁吸附方案在爬壁机器人作业领域是具有一定的应用价值的。
