舰船摇摆状态下消防炮水射流轨迹预测

邓飞云，胡洋，张宏，邓茹凤，杨田祥

(1.海军装备部驻上海地区第一军事代表室，上海 201913；2.中国船舶重工集团公司第七一三研究所 郑州市特种场所火灾防护技术重点实验室，郑州 450015)

目前，针对大型水面舰船消防炮水射流轨迹预测的研究，主要是研究消防炮俯仰角、环境风等常规因素对消防炮水射流轨迹的影响,是二维平面内的轨迹预测。而现实情况更为复杂，水射流轨迹通常受多种因素共同影响，尤其是水面舰船上消防炮水射流，其运动轨迹较大程度上还受到船体自身运动的影响。为此，考虑舰船运动的影响，建立消防炮水射流运动轨迹三维数学模型，并通过坐标变换获取船体摇摆时甲板坐标系下的水射流轨迹。

1 水射流运动轨迹数学模型

1.1 水射流运动轨迹三维数学模型

如图1所示，水射流在三维空间中主要受重力=(0,-,0)及空气阻力=(,,)作用。

图1 水射流受力示意

根据水微元运动微分方程建立水微元速度、位移以及空气阻力之间的矢量关系。

(1)

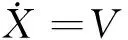
(2)

式中：=(,,)；=(,,)；=(0,-,0)；=(,,)。

分别用,,表示，，3个方向上单位向量，则水微元速度为

=++

(3)

假定海上风速为为

=w+w+w

(4)

则水射流与空气相对速度为

=-

(5)

空气阻力采用下式计算。

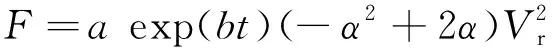
(6)

空气阻力在方向上分量为

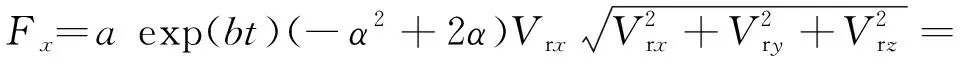
exp()(-+2)(-w)·

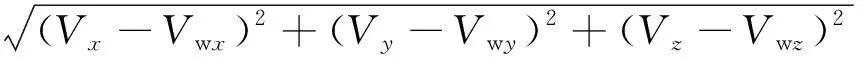
(7)

同理可得在，方向上分量分别为

=exp()(-+2)(-w)·

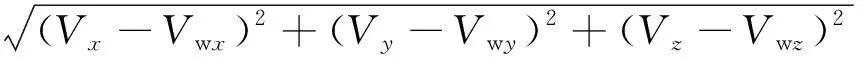
(8)

=exp()(-+2)(-w)·

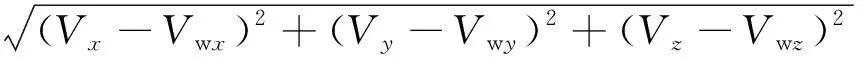
(9)

因此，建立水射流微元三维运动学微分方程组为

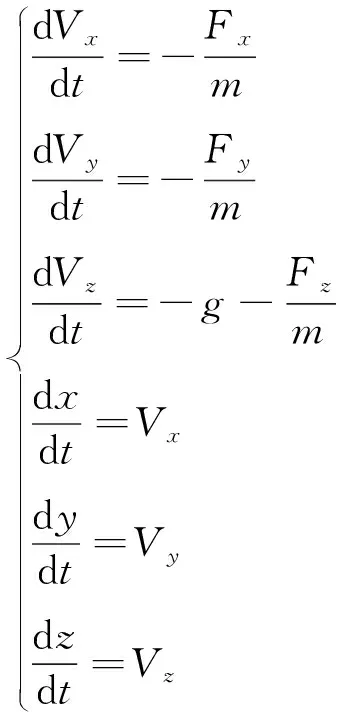
(10)

将空气阻力计算式代入上述微分方程组，并引入速度及炮口位置的初值条件，通过四阶Runge-Kutta法求解以获取水射流微元的运动轨迹。

1.2 空气阻力计算模型

常见的水射流空气阻力模型有3种，最常见的是采用常规小于音速物体(如炮弹)的空气阻力计算方法计算，考虑射流截面积的变化()及空气阻力系数给出的空气阻力计算模型，该模型的难点在于空气阻力系数及射流截面积的精确计算，具体如下。

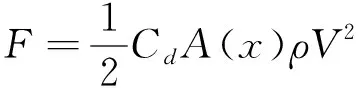
(11)

水射流的另一种空气阻力计算方法认为射流运动过程中阻力与射流轨迹行程有关，水射流运动过程中所受阻力是逐渐增大的，采用的空气阻力计算模型为

=(1+e)

(12)

式中：为射流轨迹线长；、为待定系数。该模型特点为射流轨迹的下降段比较陡。

消防炮水射流的空气阻力也应该与其俯仰角有关，因为在消防炮出口处，同样的水射流速度在不同的俯仰角下其水平方向和竖直方向的分速度不同，其阻力系数也应不同，空气阻力计算式为

=e(-+2)

(13)

式中：和为待定系数；为俯仰角,rad；为射流运动时间。

计算过程中选取的ALCO 377型消防炮并使用其射流轨迹实际曲线数据，采用第三种空气阻力计算方法得到射程具有良好的计算精度。

图2及表1为采用上述模型计算空气阻力时计算得到消防炮水射流轨迹与实际轨迹对比，本文采用消防炮30°、45°仰角时水平射程为拟合值，要求拟合误差小于1%，根据试验结果通过牛顿法迭代计算求出待定系数，60°、75°仰角模拟结果为外插值，其水平射程与实验结果误差分别0.4%和2.3%，射高误差分别3.8%和0.2%，射程误差均小于5%，计算精度可满足工程要求。

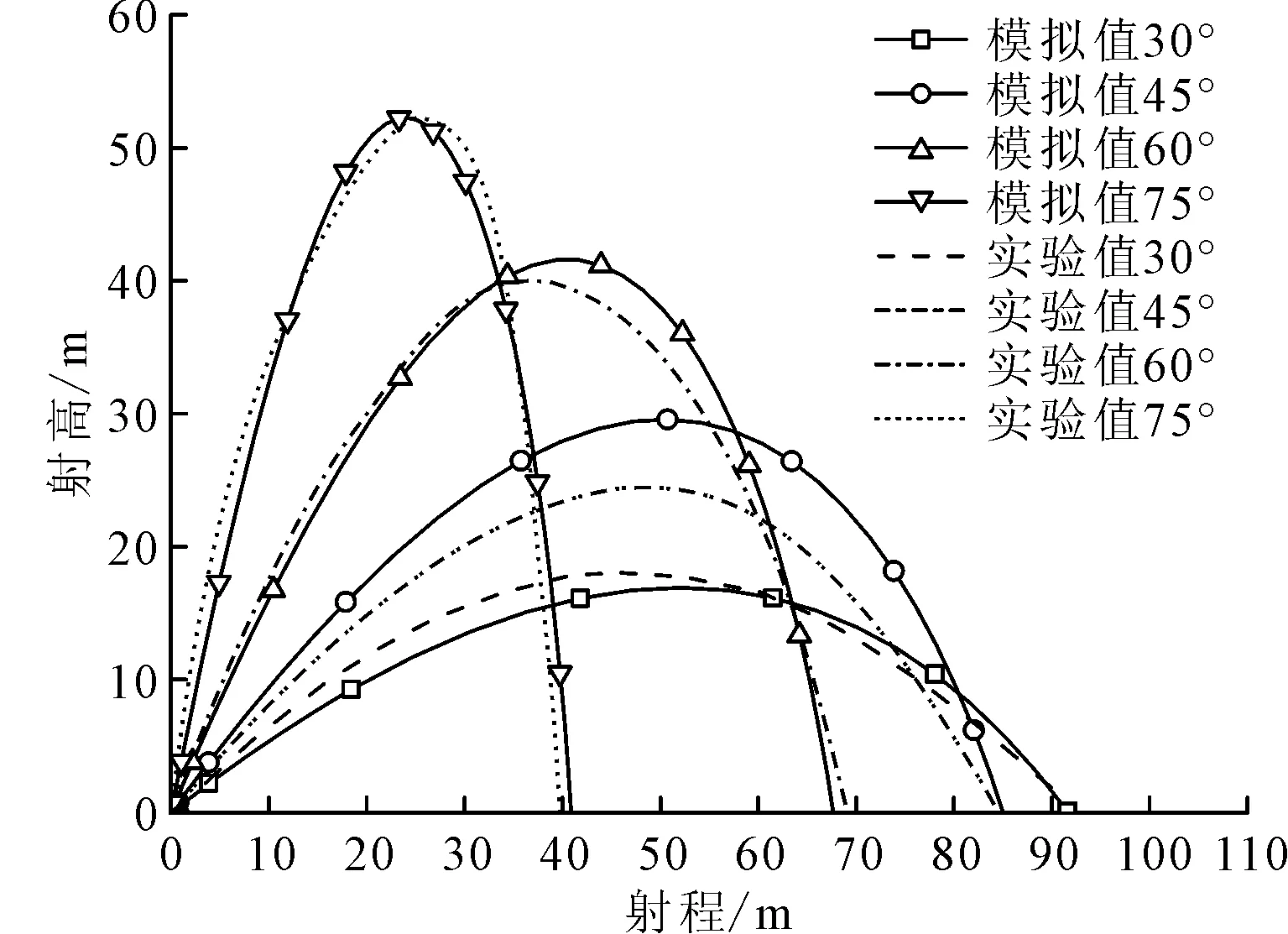
图2 消防炮射流轨迹

表1 消防水炮不同仰角时水射流轨迹的试验值与模拟值误差分析

2 船体摇摆的影响分析

在舰船6自由度运动中，横摇、纵摇和垂荡具有恢复力(矩)，可以认为是完全振荡运动，对消防炮射流轨迹影响较大。

将理想化的舰船横摇、纵摇和垂荡运动规律表述为

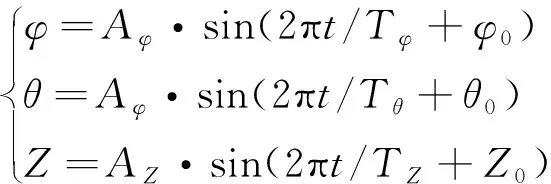
(14)

式中：、和分别为横摇、纵摇、垂荡的幅值；、和分别为横摇、纵摇、垂荡的周期；、和分别为横摇、纵摇、垂荡的初始相位角。

假设大地坐标系下水射流微元位置坐标可表示为()，甲板坐标系下为()，在船体未发生摇摆时，两个坐标系重合，并设坐标原点为消防炮位置，指向舰艏方向为正、指向左舷方向为正、指向竖直向上为正，计算过程引入坐标变换。假定摆心在甲板坐标系原点下方10 m位置处，=-10 m。

船体摇摆时，船上建筑及火灾发生位置均随着船体发生摇摆，要想精确控制消防炮进行灭火，需知道出甲板坐标系下消防炮的射流轨迹及落点位置，忽略垂荡的影响，空间一定点在横摇和纵摇后大地坐标系坐标到甲板坐标系坐标转换计算如下。

′=··

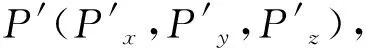
(15)

式中：为横摇变换矩阵，

(16)

为纵摇变换矩阵,

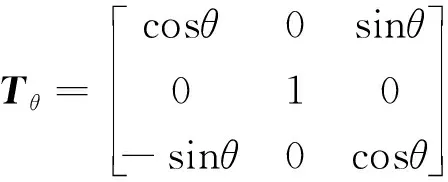
(17)

′、为点在不同坐标系下坐标矩阵，

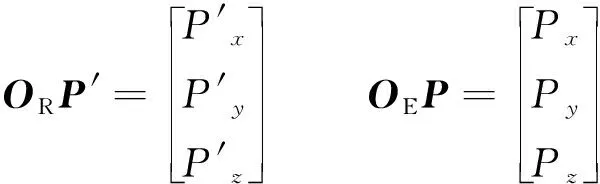
(18)

在大地坐标系下，伴随着船体摇摆运动，消防炮喷口位置及喷口速度时刻在变化，喷口位置随着船体绕着摆心作摇摆运动而改变，喷口速度为消防炮压力产生的速度与船体摇摆产生速度的合速度，可通过船体运动规律计算式得到。

对于大型水面舰船，其抗风浪能力较强，船体摇摆幅度相对较小，相对来说横摇是大型水面舰船主要摇摆运动，计算中取某大型水面舰船典型摇摆参数横摇周期为16 s，摇摆幅值为12°。则时刻大地坐标系下消防炮口位置与初速度如下。

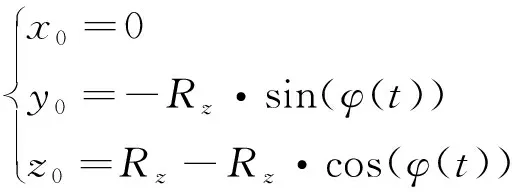
(19)

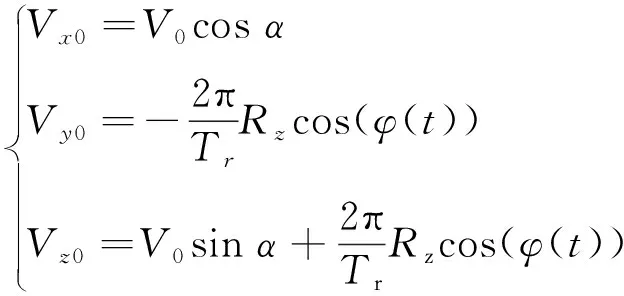
(20)

式中：为横摇中心高度方向坐标；为横摇周期；为静止状态下消防炮水射流出口初速度，为消防炮仰角。

将得到的消防炮口位置及水射流初速度作为初值条件，代入式(10)中，计算得到大地坐标系下水射流轨迹，利用得到射流轨迹上的点坐标通过上述坐标系变换的方法，转换为舰船坐标系下水射流轨迹。

3 计算结果分析

3.1 摇摆状态下水射流轨迹计算结果分析

由于大型水面舰船横摇运动相对剧烈，纵摇等其他自由度的运动较为平缓，因此主要考虑横摇对消防炮水射流轨迹的影响。船体横摇条件下消防炮射流轨迹呈周期性变化，选取典型时刻分析不同仰角下射流轨迹，=8 s时，船体横摇经过半个周期，船体回复到初始时刻位置，但摇摆方向恰好与初始时刻相反。=8 s时刻，消防炮仰角分别为30°、45°、60°、75°时水射流轨迹见图3。

由图3可见，不同仰角下船体横摇对水射流在方向上运动轨迹影响明显，方向上偏移量随着仰角的增加而增大，30°仰角时，方向上偏移量仅为1.875 m，仰角增加至75°时，方向上偏移量达到3.690 m。此外，从图中射流轨迹形状可以看出，仰角越大，空中侧向偏移量越大，射流在空中运动轨迹越复杂。

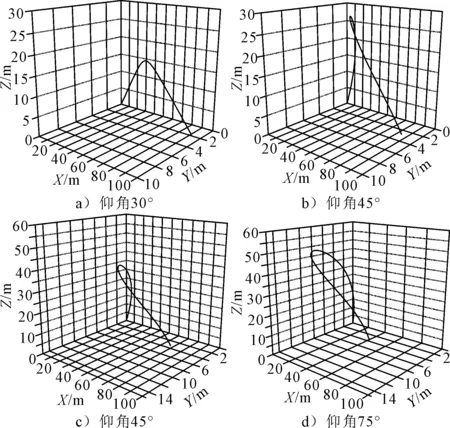
图3 不同仰角下消防炮射流轨迹

3.2 摇摆状态下环境风对水射流轨迹影响分析

海上环境复杂，舰船摇摆状态通常也伴随环境风，风速和风向对消防炮射流轨迹均有较大的影响。分析消防炮仰角=45°时，舰船摇摆状态下不同风速、风向对水射流轨迹的影响。

舰船摇摆状态下不同环境风速时水射流轨迹见图4。横摇时间为一半横摇周期=8 s，图中ⅰ、ⅱ、ⅲ、ⅳ曲线分别是风速为0、5、10.0、13.8 m/s时的射流轨迹，对应海况等级分别为0级、3级、4级、5级。

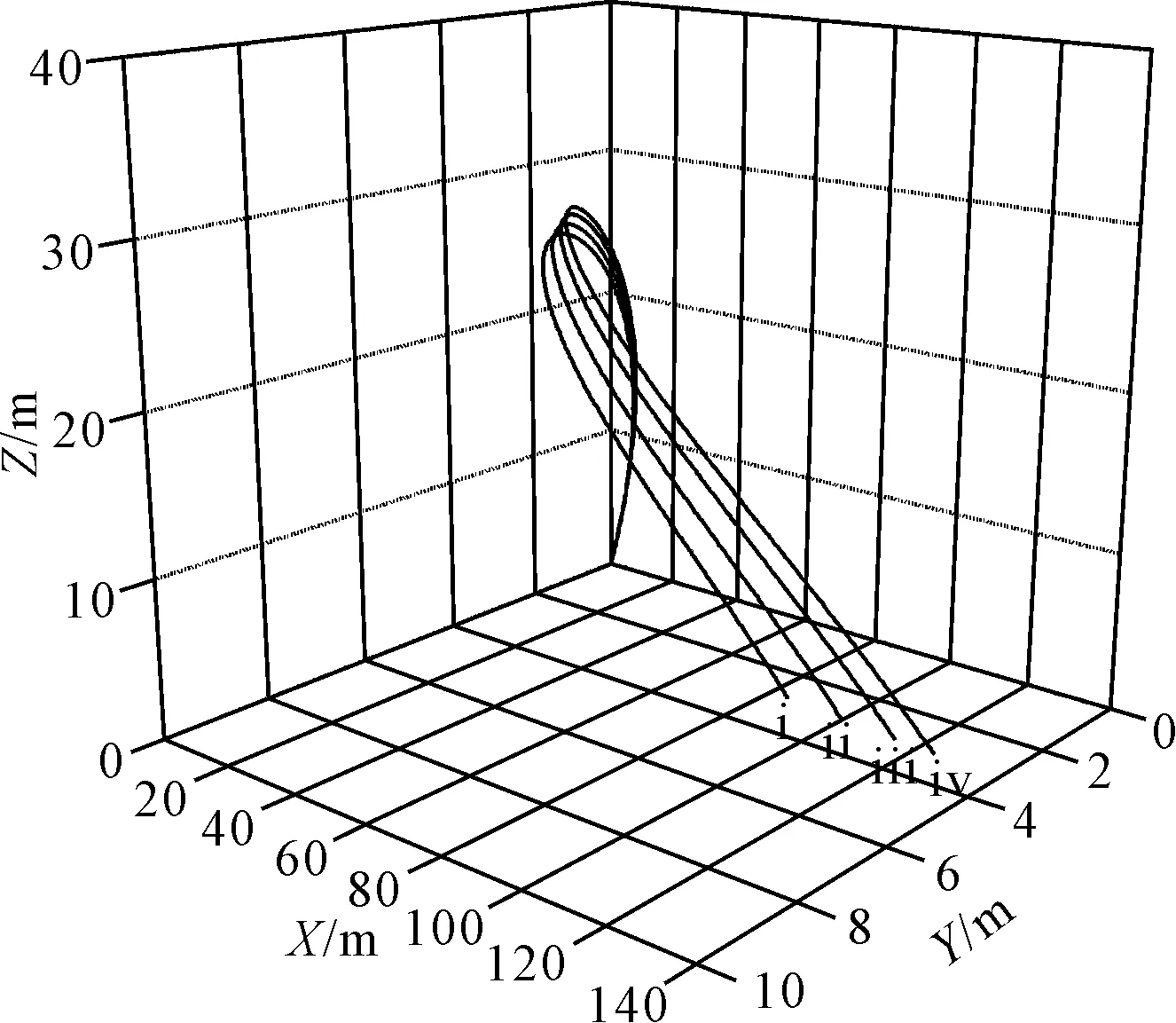
图4 不同风速条件下消防炮射流轨迹

由图4可见，顺风风速对消防炮射程有着有利影响，可增加消防炮射程，无风时，船体摇摆条件下消防炮水平射程仅为84.63 m，而风速达到13.8 m/s，消防炮水平射程达到为124.45 m，射程增加了47%。此外，随着风速的增加，方向上射程及射高均有小幅度增加。

不同风向时水射流轨迹见图5，计算选取五级海况下环境风速为13.8 m/s。

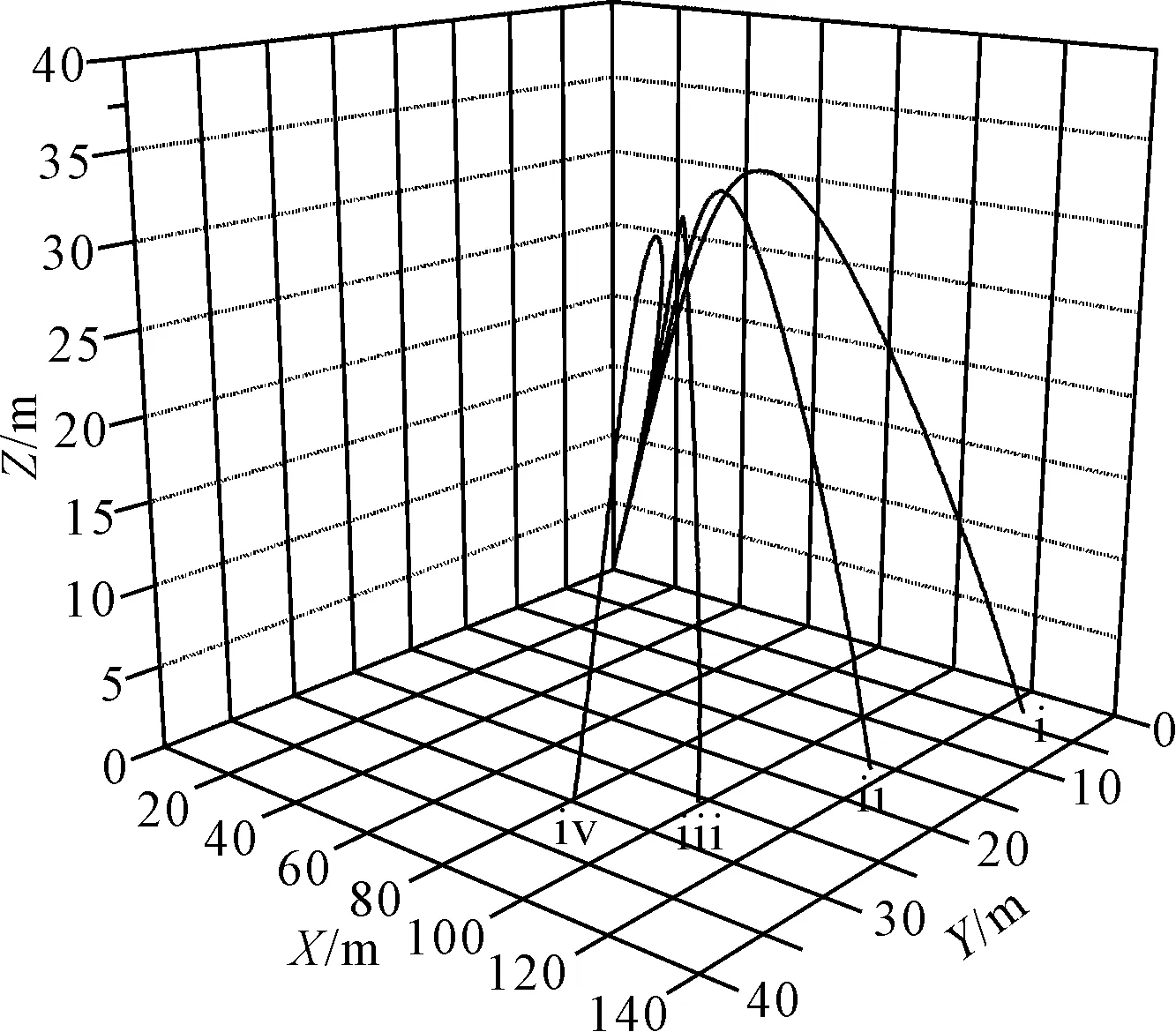
图5 不同风向条件下消防炮射流轨迹

图5中ⅰ、ⅱ、ⅲ、ⅳ射流轨迹曲线对应风向分别为0°，30°，60°，90°。可以看出，在横摇条件下风向对消防炮射程有较明显的影响，随着环境风与轴正方向夹角的增大，消防炮射流轨迹与落点明显向轴正向偏移，方向射程明显减小，方向偏移量明显增加。五级海况下，当风向与水射流初始方向垂直时，风向可导致落点轨迹在方向有30 m的偏移量。

4 结论

1)船体横摇状态下消防炮射流轨迹呈周期性变化，横摇对水射流在船宽方向上运动轨迹影响明显，并且消防炮仰角越大，水射流落点位置沿船宽方向上偏移量越大，仰角达到75°时，水射流落点位置在船宽方向上偏移量可达到3.69 m。

2)风速对消防炮射程有明显的影响，顺风时环境风可大大增加消防炮射程，五级海况下，消防炮水平射程可增加47%，同时可小幅增加射及船宽方向上偏移量。

3)船体横摇状态下风向对消防炮射程有较大的影响，随着环境风与船长方向夹角的增大，消防炮射流轨迹与落点明显向船宽偏移量增加，五级海况下，风向与水射流初始方向垂直时，风向可导致落点轨迹在船宽方向有30 m的偏移量，落点位置沿船长方向射程明显减小，射程减小量可达45 m。