某变射速航炮缓冲装置动力学特性优化研究

田楠，赵建中，李勇，王开政，裴春

(1.西北机电工程研究所，陕西 咸阳 712099；2.内蒙古北方重工业集团有限公司，内蒙古 包头 014033)

某航炮在实际使用中要求变射速，低射速主要用于对敌方地面目标实施精确点打击，高射速要求对敌方的空中目标有一定的空战能力。航炮变射速对缓冲装置结构参数设计带来新的挑战，缓冲装置既要求射击时航炮最大后坐阻力小，又要与航炮的射速相匹配，否则会导致航炮后坐力叠加，影响航炮射击稳定性与射击精度[1-2]。

目前国内对适应变射速的缓冲装置研究资料较少。文献[3]以某小口径自动炮为研究对象，提出了一种新型摩擦阻尼缓冲器，建立了其刚柔耦合动力学虚拟样机模型，通过仿真对比了不同射速和不同摩擦阻尼缓冲器参数时炮身运动规律。

笔者提出一种结构简单、适应航炮变射速的缓冲装置，建立其动力学运动方程，在后坐位移一定时，分析弹簧预压力和刚度系数对航炮后坐力影响规律，并以后坐力最小为优化目标，对其动力学特性进行优化研究。

1 航炮缓冲装置结构原理

环形弹簧在工作时由于其特殊的结构特性，接触表面产生很大的摩擦力，摩擦力会把较大部分后坐能量转换为热能释放到空气中耗散掉，因此其缓冲减振能力很高[4]。缓冲装置主要由前连接杆、弹簧挡板、外环形弹簧、内环形弹簧、后连接杆、垫片、外筒和固定螺母组成。具体结构如图1所示。

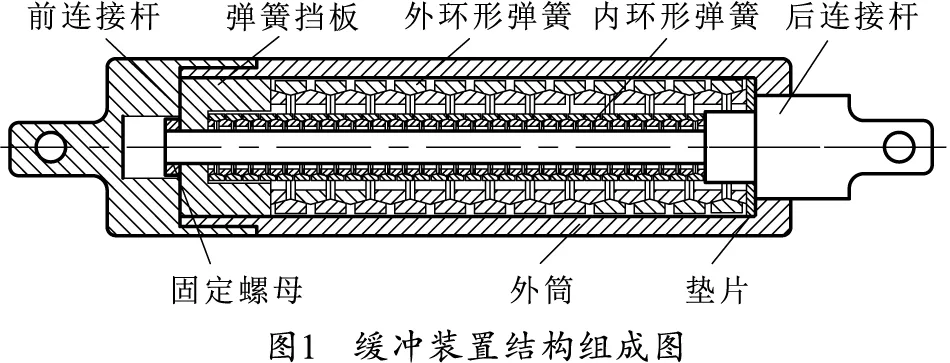
前连接杆和身管通过圆柱销连接，后连接杆通过圆柱销与摇架连接。航炮击发时，在火药燃气作用下，航炮后坐带动前连接杆、外筒和弹簧挡板向后运动，压缩外环形弹簧和内环形弹簧，吸收航炮后坐能量，环形弹簧的弹簧力是航炮后坐时的主要阻力；后坐过程结束，航炮在内外环形弹簧作用下复进，推动前连接杆、外筒和弹簧挡板向前运动，由于后坐能量的60%～70%被环形弹簧接触表面摩擦力转化为热能消耗掉，因此环形卸载时的刚度较加载时的刚度小，减少了航炮阻振时间；复进到平衡位置后，由于惯性作用继续前冲，此时弹簧挡板被固定螺母挡住，保持不动，外筒带动垫片压缩外环形弹簧，此时只有外环形弹簧工作，控制前冲力小于后坐力，当前冲的惯性运动停止后，外环形弹簧由最大压缩状态开始伸长，在弹簧力作用下又返回平衡位置，如此反复形成振荡。但由于摩擦力的阻振作用和能量的消耗，航炮会迅速停止下来进行下一发射击。

2 航炮缓冲装置动力学建模

2.1 基本假设

根据缓冲装置结构特点和工作过程，建立其动力学模型，主要假设如下：

1)忽略运动副间的间隙；

2)不考虑环形弹簧内部阻尼；

3)不考虑航炮内部机构运动对缓冲性能影响；

4)不考虑航炮垂直于后坐方向的运动对缓冲装置性能影响。

根据以上假设，将航炮缓冲装置简化为弹簧-质量振动系统，其所建立的物理模型如图2所示。

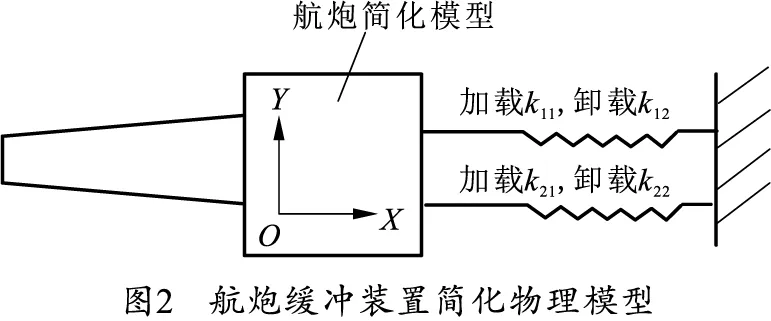
2.2 航炮缓冲装置数学模型

航炮缓冲装置在其连续发射过程中振动响应问题最终归结为有阻尼受迫振动，振动微分方程可表示为

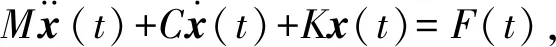
(1)

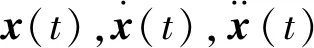
以航炮质心O的初始位置为起始点建立坐标系，规定力的方向向后为正方向，向前为负方向；位移离开平衡位置向后为正，向前为负[5-8]。对于受迫振动系统，航炮运动的微分方程为：

(2)

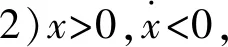
(3)

(4)

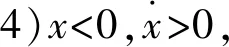
(5)

式中：mh为航炮后坐质量；x为航炮后坐位移；Fpt(t)为航炮炮膛合力；θ为火炮高低射角；F0为内、外环形弹簧预压力之和；Ff为航炮与摇架导轨的摩擦力；k11为外环形弹簧的加载刚度；k12为外环形弹簧的卸载刚度；k21为内环形弹簧的加载刚度；k22为内环形弹簧的卸载刚度；环形弹簧加载刚度k11、k21与卸载刚度k12、k22关系为

(6)

式中：β为环形弹簧的圆锥角，结合环形弹簧接触面的加工精度取值为14°；ρ为环形弹簧的摩擦角，结合环形弹簧接触面的加工精度和承受载荷，取值为8.5°。

炮膛合力Fpt为

(7)

式中：φ为次要功计算系数；q为弹丸的质量；p为火药气体的平均压力；ω为装药量；S为炮膛断面面积；pg为后效期开始炮口压力；χ为炮口制退器冲量特征量；b为时间常数；t为以内弹道开始为起点的计算时间；tg为炮口时间点；tk为后效期结束时间点。

3 航炮缓冲装置设计参数分析

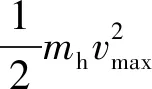
(8)

式中：vmax为航炮后坐最大速度；xhmax为航炮最大后坐位移。

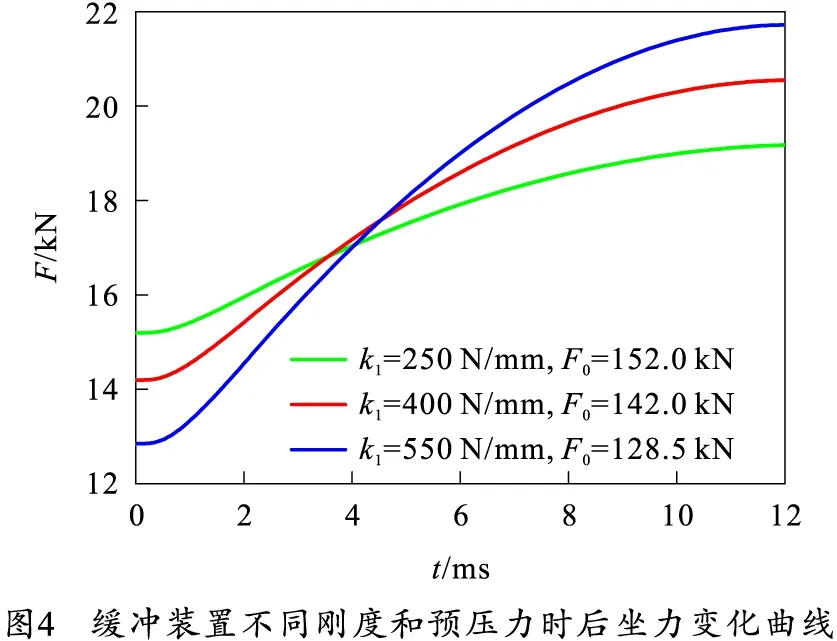
笔者主要研究在最大后坐位移一定时，环形弹簧加载时的刚度系数k1和环形弹簧的预压力F0对航炮最大后坐力影响规律。因此将环形弹簧加载时的刚度系数k1和环形弹簧的预压力F0作为缓冲装置设计变量，分析其对后坐力影响结果，结果如图3、4所示。

由图3、4可以看出，航炮最大后坐位移一定时，最大后坐力与环形弹簧加载时的刚度系数k1和环形弹簧的预压力F0变化规律，即预压力F0越大，刚度系数k1越小，则航炮的最大后坐力越小。

4 航炮缓冲装置优化模型

结合缓冲装置实际使用条件和航炮对缓冲装置特殊需求，建立缓冲装置约束条件和优化模型[10]。

4.1 缓冲装置优化仿真计算工况

笔者仿真计算了射角为0°时的后坐力。航炮内弹道和后效期持续时间14.6 ms，航炮射击时所受的炮膛合力如图5所示。

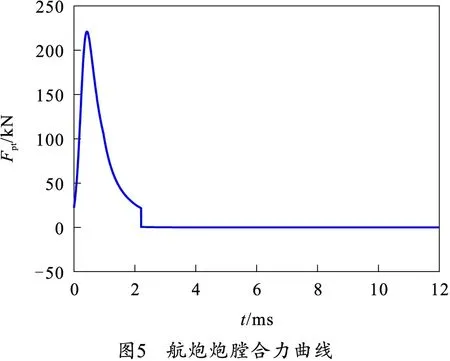
4.2 缓冲装置约束条件建立

航炮缓冲装置参数设计需满足以下要求：

1)预压力除能减小后坐力外，还能保证航炮恢复并保持在平衡位置，故在设计时应使预压力大于摩擦力及全炮在使用过程中承受的过载与本身质量乘积之和。全炮在使用过程中承受的过载一般取(3～4)mhg。即：

k1H0≥Ff+(3～4)mhg.

(9)

2)航炮的总位移xz(mm)等于最大后坐长xhmax(mm)与最大前冲长xqmax(mm)，xz太大会使航炮在飞机安装架上安装困难，易发生构件相撞问题。即：

(10)

3)航炮射击全阻振时间T应小于航炮一个工作循环的时间，否则会导致后坐力叠加，缓冲器因过载而损坏。即：

T≤TA,

(11)

式中，TA为航炮一个工作循环的时间，低射速为0.1 s，高射速为0.033 s。

4)考虑缓冲装置结构合理布局与尺寸参数设计，环形弹簧加载时的刚度系数k1(N/mm)和环形弹簧的预压量H0(mm)取值需在式(12)范围内：

(12)

4.3 缓冲装置优化模型建立

基于构建的优化数学模型，笔者选用第2代带有精英保留策略的非支配排序的遗传算法(NSGA-Ⅱ)对航炮缓冲装置参数进行优化。首先对航炮缓冲装置结构设计参数的初始种群进行非支配排序，通过遗传算法生成第1代缓冲装置设计参数种群，然后对第1代种群进行交叉变异等操作，得到下一代种群，并将子代和父代种群进行合并，对新生成的种群进行快速非支配排序，选择生成新的父代种群，然后重复上述操作流程，直到计算停止[11-15]。

取航炮最大后坐阻力最小为目标函数，优化的数学模型描述如式(13)、(14)所示。

minFRmax(t)，

(13)

(14)

通过遗传算法，利用MATLAB软件编程得到缓冲装置结构参数的最优解，如表1所示。其中，k11取60 N/mm，k21取40 N/mm，则优化后的环形弹簧加载时刚度系数k1为100 N/mm，环形弹簧预压力F0为15.20 kN；优化前的环形弹簧加载时刚度系数k1为250 N/mm，环形弹簧预压力F0为14.82 kN。

表1 航炮缓冲装置结构参数优化前后结果

5 数值计算及结果分析

缓冲装置射速600 发/min时，7连发优化前后的后坐位移曲线和后坐力曲线如图6、7所示。

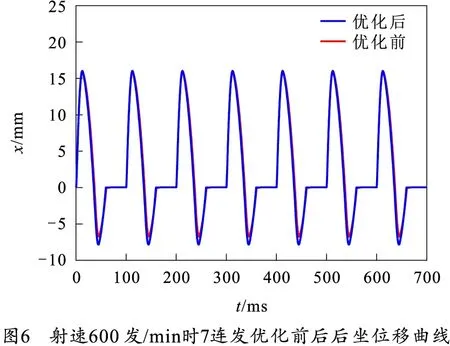
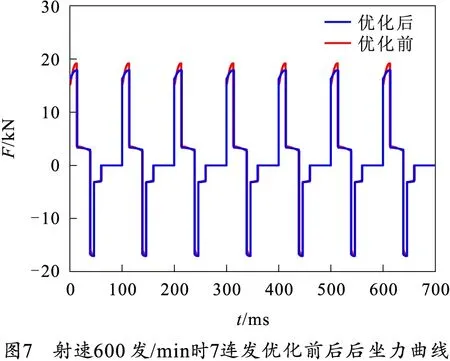
由图6、7可以看出，在航炮射击后，航炮在缓冲装置作用下首先由平衡位置进行后坐，后坐到位后进行复进，复进到平衡位置后，由于惯性作用继续前冲，当前冲的惯性运动停止后，在弹簧力作用下又返回平衡位置，如此反复形成振荡。但由于摩擦力的阻振作用和能量的消耗，航炮会迅速停止下来进行下一发射击。

缓冲装置射速600 发/min优化前后仿真结果对比如表2所示。可以看出在优化前后后坐位移基本相同条件下，优化后的最大后坐力较优化前的最大后坐力减少13.4%，优化后的最大前冲力较优化前的最大前冲力增加1.1%。

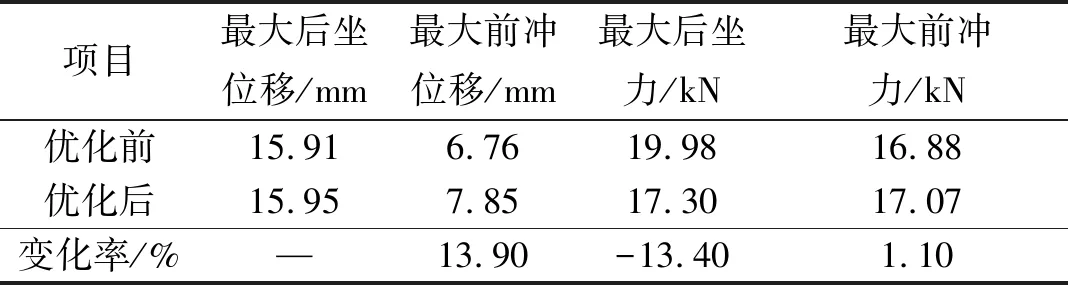
表2 缓冲装置射速600 发/min优化前后仿真结果对比

缓冲装置射速1 800 发/min时，7连发优化前后的后坐位移曲线和后坐力曲线如图8、9所示。

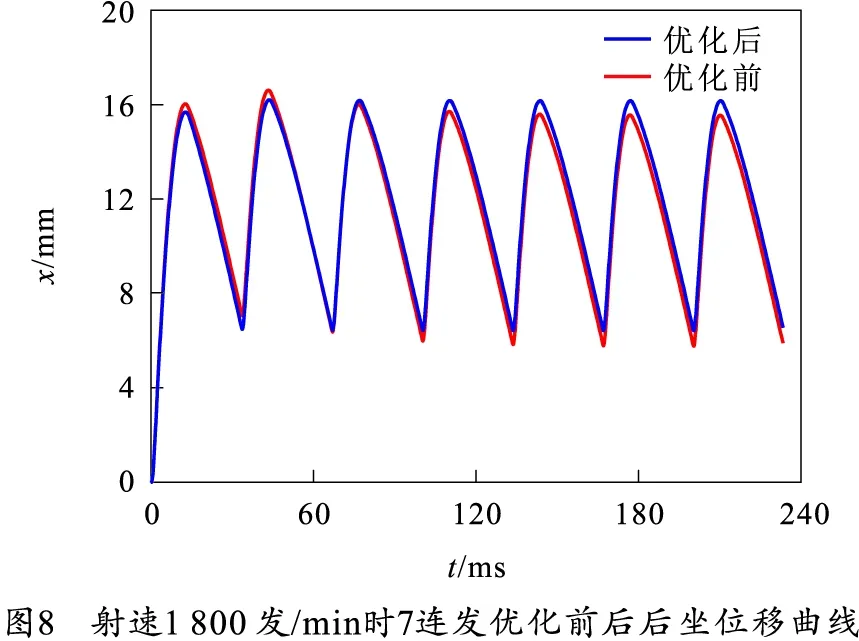
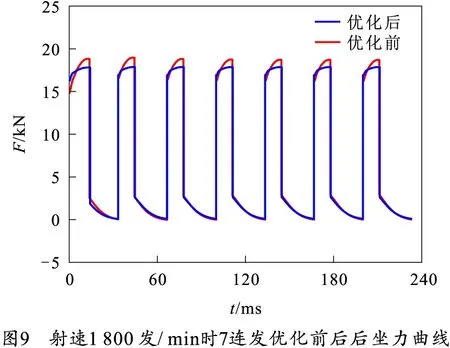
由图8、9可以看出在航炮射击后，航炮在缓冲装置作用下首先由平衡位置进行后坐，后坐到位后进行复进，复进到到平衡位置前，下一发已开始射击，实现浮动。

缓冲装置射速1 800 发/min优化前后仿真结果对比如表3所示。可以看出在高射速情况下，缓冲装置最大前冲位移和最大前冲力都为0，实现浮动射击。在优化前后后坐位移基本相同条件下，优化后的最大后坐力较优化前的最大后坐力减少12.3%。

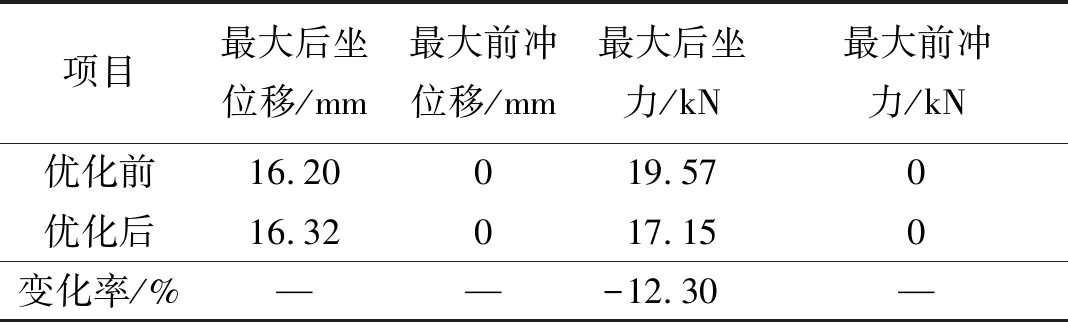
表3 缓冲装置射速1 800 发/min优化前后仿真结果对比

6 结论

通过建立航炮缓冲装置的动力学模型，并以后坐力最小为优化目标，缓冲装置结构参数设计为约束条件，在此基础上对其进行优化设计，进行优化前后数据的对比分析，可以得出以下结论：

1)缓冲装置在射速600 发/min和1 800 发/min射击时，在后坐位移基本相同条件下，优化后最大后坐力较优化前分别减少13.4%和12.3%，优化后缓冲装置的动力学特性得到明显改善。

2)缓冲装置在射速600 发/min优化前后的最大后坐位移和最大后坐力，与射速1 800 发/min优化前后的最大后坐位移和最大后坐力基本相同，说明在缓冲装置参数确定条件下，射速对航炮最大后坐位移和最大后坐力影响很小。

3)通过合理匹配射速和缓冲装置设计参数，可以有效避免变射速射击时的后坐力叠加现象，使其能够适应航炮变射速射击。其中缓冲装置在射速1 800 发/min实现浮动射击，航炮浮动射击时受力方向始终保持向后不变，这对提高航炮射击的稳定性和射击精度极为有利。