新能源电力系统频率控制研究

文/冯笑非

0 引言

为解决因传输时滞不确定、负荷扰动、系统参数以及新能源间歇性功率所带来的系统调频功能下降问题，文章提出了基于控制信号变周期采样的PI负荷频率控制方案。该方案能够结合采样网络，运用静态输出反馈方法来完成电力系统采样PI负荷频率控制(Sampling PI Load Frequency Control，SPI-LFC)方案构建。该方案在构建完SPI-LFC方案模型后，运用双边闭环型Lyapunov泛函，经与自由矩阵不等式的结合来获得系统设计低保守性稳定准则与SPI控制器的方法。经对结果进行仿真分析，发现LFC方案能够优化电力系统参数与通信网络运行过程中产生失稳问题的控制效果。

近几年，风电与太阳能等新能源发电，已经成为实现二氧化碳排放控制目标的重要途径。随着新能源发电行业的快速发展，风电与太阳能发电已经被广泛运用到电力系统中。但受风速与气候条件变化的影响，风电与太阳能发电站所输出的波动功率会对系统运行频率的稳定性造成影响。新能源并网发电多是采用低电压穿越、最大功率跟踪的方式，因而，实现的输出方式是有功与无功解耦的单位功率因数。由此可见，大规模接入风电与太阳能等新能源发电，会对当前电力系统运行的转动惯量造成影响。其中，影响之一即负荷扰动，会导致电力系统运行出现较大频率波动，甚至会出现失稳问题。为解决这一问题，研究人员基于新能源发电的随机性、规模大以及接入参数不确定等特性，提出智能控制措施。

本文研究的是基于控制信号变周期采样的SPI-LFC方案。其主要运用采样网络环境中的静态输出反馈方法，构建电力系统模型。此后运用采样区间[tk，tk+1)信息，形成全新的采样区间双边闭环型Lyapunov泛函。如此就可运用自由矩阵积分不等式对泛函导数中的积分项进行估算，以推导相关的电力系统稳定准则。借助得出的准则，就可运用电力系统SPI控制器设计方法以及仿真分析方法，验证方案的有效性与科学性。

此过程主要将三区域LFC系统作为方案验证分析对象。采用的记号有：上标“-1”和“T”表示为矩阵逆与转置；0和I分别表示为合适维度下零矩阵与单位矩阵；“＊”表示为对称矩阵中的对称项；任意矩阵X＞0表明矩阵X为正定；diag{·} 表示对角阵；sym{N}表示N+N T。

1 基于多区域的SPI-LFC模型构建

1.1 面向新能源出力不确定性的连续LFC模型构建

与传统电站发电电源不同，风电与光伏等新能源的出力存在不确定性因素。特别是气候条件变化所带来的影响，会增加功率预测工作开展的难度，进而造成实际输出功率与预测功率间存在偏差。故而，研究人员将模型负荷位置接入输出功率偏差为负的负荷扰动项。其组成部分有：调速器模块、发电机负载模块、原动机模块、连接线模块、线性调频控制模块以及采样数据网络模块。

在采用静态输出反馈控制方法的过程中，为使LFC控制器具备调节频率与联络线功率的误差功能，可将ACEi信号的积分控制项设置在模型中。成功采用Laplace逆变换，并选出具有适应性的状态量。其中i区域LFC状态的空间方程为：

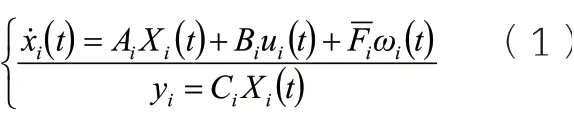
其中，

式 中：xi，ui，ωki（k=1，2）和yi分别为第i个区域的状态向量、控制输入、外部扰动输入和输出向量；为联络线功率系数；△fi，△Pci，△Pvni，△Pmni，△Pdi与△PREi分 别表示控制区域i的频率偏差、控制输入变化量、阀门开度变化量、机械功率变化量、负荷扰动与新能源功率偏差扰动；Mi和Di分别表示系统的旋转惯量和阻尼系数；Rni，αni与βi分别表示调速器调节系数、发电机的参与系数与频率偏差系数；△Ptie-i表示联络线交换功率偏差；Tij表示控制区域i和j的联络线同步系数；Tgni与Ttni分别为调速器与汽轮机的时间常数；ACEi(ACEi=βi△fi+△Ptie，i)为区域i控制偏差。

1.2 变周期采样的SPI-LFC模型建立

对于采用广域网络信息参与控制的电力系统，即使是定期地采集与发送数据，但通信网络阻塞或数据丢失等故障会导致信息传输时延，使得控制对象接收到的数据仍然是非周期的。所以，在采样控制中，考虑变周期采样非常有意义。tk，k=1，2，…表示采样点对应信号的采样时刻，满足：0=t0＜t1＜t2，…＜limk→∞tk=+∞。定义零阶保持器(Zero Order Hold，ZOH)端控制信号更新时刻tk，与tk+1之间的时间间隔为采样周期hk。满足如下条件：

式(2)中，h1和h2分 别 表示采样周期的下界和上界。在传输过程中，不存在数据丢包、错序等故障时，有h1=h2，即采样周期为固定值。如果有网络传输故障，将使得h1＜h2，即不同的tk，其hk大小也不同，体现了采样周期的变周期性。

在静态输出反馈控制中，将yi(t)作为控制信号输出，并且，在采样控制模式下，只利用采样时刻t=tk的测量信号yi(tk)生成输入控制信号，即：

式中，Ki为电力系统区域i的采样PI静态输出反馈控制器增益。将式(3)代入系统(1)，可得闭环电力系统变周期采样的SPI-LFC模型

系统在平衡点内部稳定，可转化为设计稳定控制器，使如下电力系统在原点稳定。

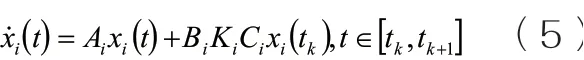
2 实例分析

采用理论计算与仿真分析结合的方式来验证新能源接入3个区域电力系统的实际情况，能够确定方案运用的科学有效性。假定控制区域设置的发电机组数为2台。

2.1 控制器设计

假设电力系统3区域采样周期为4秒，h=4秒，调整参

2.2 分析控制器性能与仿真验证

3区域的电力系统均安装了控制器K31与K32，当系统逐渐进入稳定状态，λ=0时，采用的定量与算法均为1。计算能够得出，不同区域允许最大采样周期MASPc(s)，以控制器K32为例，当h=4秒，采用1定理、算法。

情形1：仿真测试K31和K32在不同采样周期下，对负荷扰动的鲁棒性。

假设在t≥0秒时刻，3区域中的阶跃负荷扰动情况如下：

从图1可知，当h=2秒与h=4秒时，控制器K31和K32都能保持电力系统频率对外部扰动的鲁棒性。当h=8秒时，控制器K31将失去对频率稳定的控制作用，而本文所设计的控制器K32仍然能保持对频率稳定性能的控制。因此，与控制器K31相比，本文所设计的控制器K32，使电力系统具有相对较大的采样周期稳定裕度。

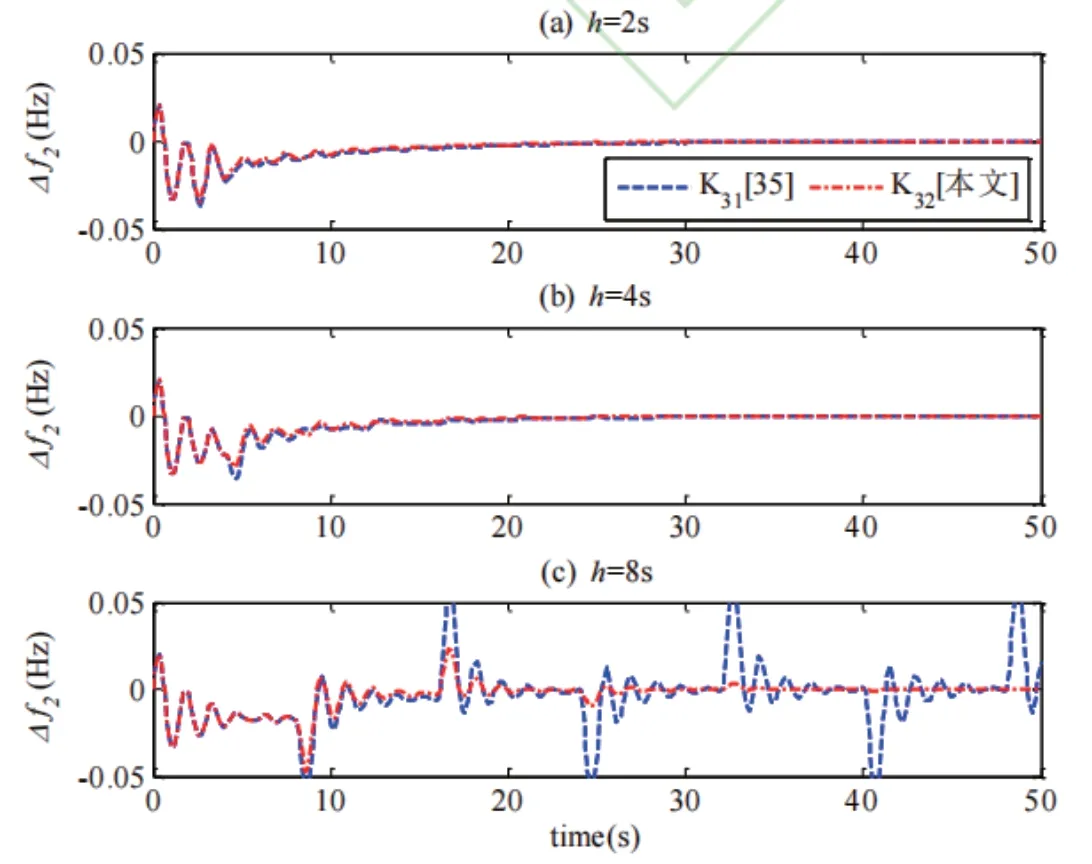
图1 不同h条件下的 响应曲线

情形2：采用仿真分析法测试控制器K31与K32处在相同采样周期与随机负荷扰动下，电力系统的鲁棒性能是否受到影响，并得出验证结果。

当新能源发电渗透率提升，系统惯性常数M和频率偏差系数β会下降，但下垂系数R会增加。而且外部参数变化会给系统LFC性能带来负面影响。以下内容为仿真验证分析，相同采样周期与负荷扰动环境下，外部参数鲁棒性能是否发生变化。在情形3环境下，外部负荷与新能源随机扰动功率输入，h=7秒，获得了4种惯性常数减少情况下频率偏差 。

新能源运用恒功率控制模式接入电网后，会随着新能源比例提升。当电力系统运行产生的相对惯性系数发生参数变化，对LFC进行动态调整，就会导致 超调量增加。而处在采样周期环境下，惯性常数下降了30%，采样控制器K31就无法为电力系统运行频率的稳定性提供保障。本文设计采用的控制器K32即使是在惯性常数降低到40%，仍能保持电力系统运行频率的稳定效果，且收敛率不受影响。

4 结语

综上所述，对于新能源接入电力系统造成的参数与负荷扰动不确定性问题，提出了基于信号控制的变周期采样SPILFC方法。经对算例进行仿真验证分析，得出了以下结果：

（1）本文研究方法，确定的采样周期稳定性与指数收敛率，要优于现有方法。即采样周期越大，可容忍的电力系统通信时滞就越大。此外，还能在降低网络通信负担的同时，减轻控制器设计计算工作难度。

（2）当新能源随机功率的偏差扰动与渗透率较高，也可实现电力系统运行频率的稳定控制。这表明，基于采样周期控制的方法，可针对负荷扰动、新能源随机扰动与不确定性参数发挥出更好的鲁棒性。不仅能够有效提升新能源电力系统运行控制渗透率，还能为接入电力系统LFC提供一种思考问题的路径与方法。