浅谈线性代数兴趣教学

◎肖 霞 田苗青 李永凤

(郑州轻工业大学数学与信息科学学院,河南 郑州 405002)

线性代数是高等院校理工科非数学专业一门重要的公共基础课,是理工科学生必备的数学工具.该课程主要包括行列式、向量与图形、矩阵、n维向量与线性方程组、特征值与特征向量、二次型等内容.其基本教学目的是使学生系统地理解、掌握相关的基本概念、基本理论、基本思想、基本方法和基本技能,为后继课程的学习奠定基础.该课程具有较强的抽象性与逻辑性,许多初学者认为这是一门枯燥难学的课程.为了提高初学者的学习兴趣,提升本门课程的授课质量,本文从以下方面探讨兴趣教学.

一、问题驱动,吸引学生

以学生经常接触且比较感兴趣的内容为背景设置问题,能让学生产生共鸣,使学生全身心投入课堂教学.

如矩阵概念的提出比较突然,它有什么应用呢?受山东大学秦静老师的启发,为了自然引入矩阵概念,可以以无人机表演为背景,设置如下引例,吸引学生的注意力.

引例:5名学生(小王、小陈、小鲁、小沈、小安)参加无人机表演,出发时无人机按序号从左往右排列,无人机机身颜色有黄色、蓝色、橙色、绿色、红色,遥控手柄形状有正方形、椭圆形、梯形、三角形、马鞍形,无人机携带烟雾颜色有红色、黄色、白色、绿色、蓝色.这5名学生喜欢组团玩王者荣耀游戏,在游戏中他们喜欢使用法师、刺客、坦克、射手、战士.根据以下信息,回答问题.

1红色无人机在中间;

2最右边的无人机使用椭圆形手柄;

3挨着椭圆形手柄无人机的操作者在游戏中喜欢使用法师;

4最左边无人机的操作者在游戏中喜欢使用战士,他右边的操作者在游戏喜欢使用坦克;

5使用三角形手柄的操作者在游戏中喜欢使用射手;

6在游戏中喜欢使用刺客的是小安,与他操控的无人机相邻的那个无人机携带白色烟雾;

7携带白色烟雾的无人机机身是橙色,用梯形手柄;

8小沈操控的无人机在小安的左边;

9在游戏中喜欢使用战士的操作者操控黄色无人机;

10小陈操控蓝色无人机;

11小王使用正方形手柄;

12黄色无人机携带蓝色烟雾,与它相邻的无人机携带绿色烟雾;

13用三角形手柄操控的无人机机身颜色和携带烟雾颜色一样.

问题:3号无人机携带什么颜色的烟雾?小安操控的无人机携带什么颜色的烟雾?

这个问题可以用列表法来解决.

第一行从左往右对无人机的顺序进行编号,第一列是无人机的相关信息,如表1所示.

由条件1可知3号无人机机身颜色是红色,则表2为对应表格.

由条件2可知5号无人机使用椭圆形手柄,则对应表格为表3.

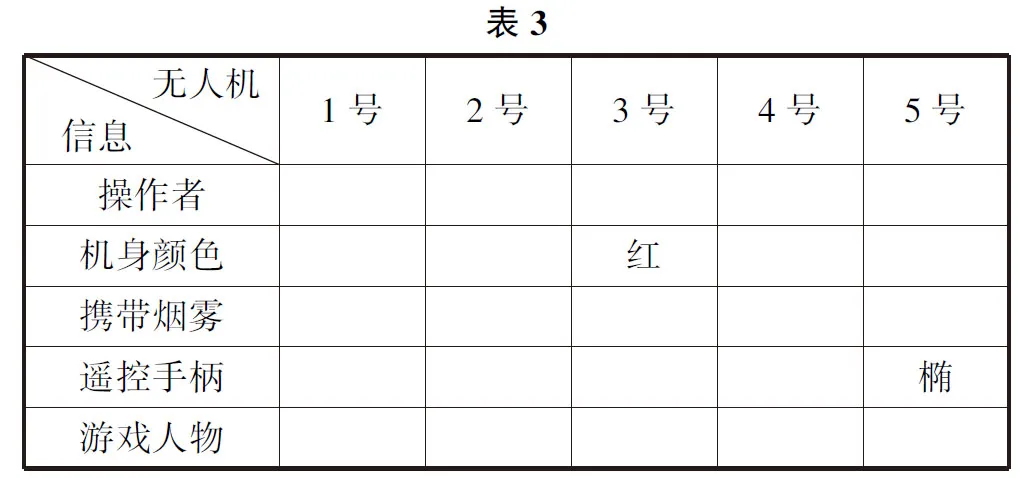
由条件3可知4号无人机的操作者在游戏中喜欢使用法师,对应表格为表4.

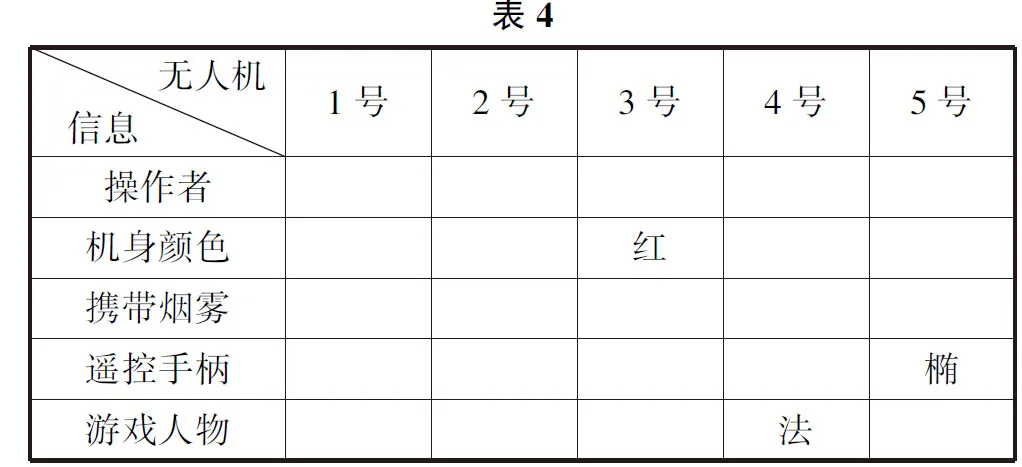
由条件4可知1号无人机的操作者在游戏中喜欢使用战士,2号无人机的操作者在游戏中喜欢使用坦克,则对应表格为表5.

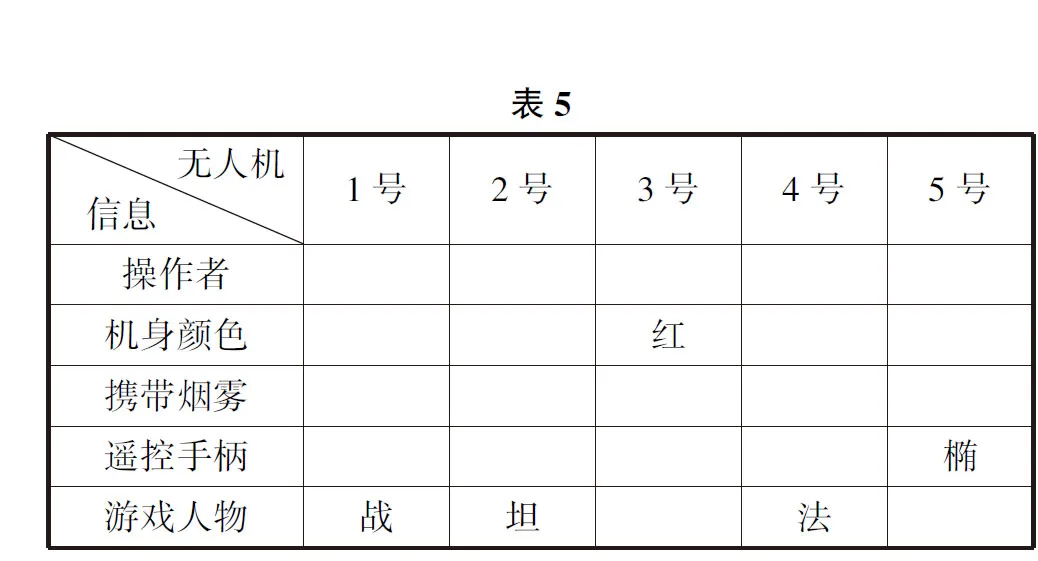
由于1号、2号、4号无人机的操作者在游戏中喜欢使用战士、坦克、法师,而5号无人机的遥控手柄是椭圆形,所以满足条件5的只能是3号无人机,即3号无人机的遥控手柄是三角形,其操作者在游戏中喜欢使用射手,则对应表格为表6.

由于5名学生在游戏中喜欢使用法师、刺客、坦克、射手、战士,所以游戏人物“刺客”只能是5号无人机操作者在游戏中喜欢使用的角色,则对应表格为表7.

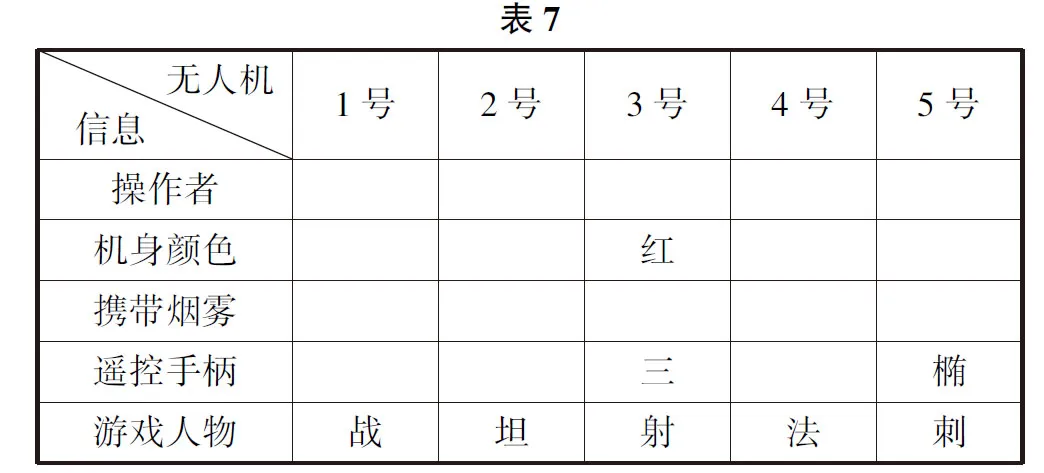
由条件6可知5号无人机的操作者是小安,4号无人机携带白色烟雾,则对应表格为表8.

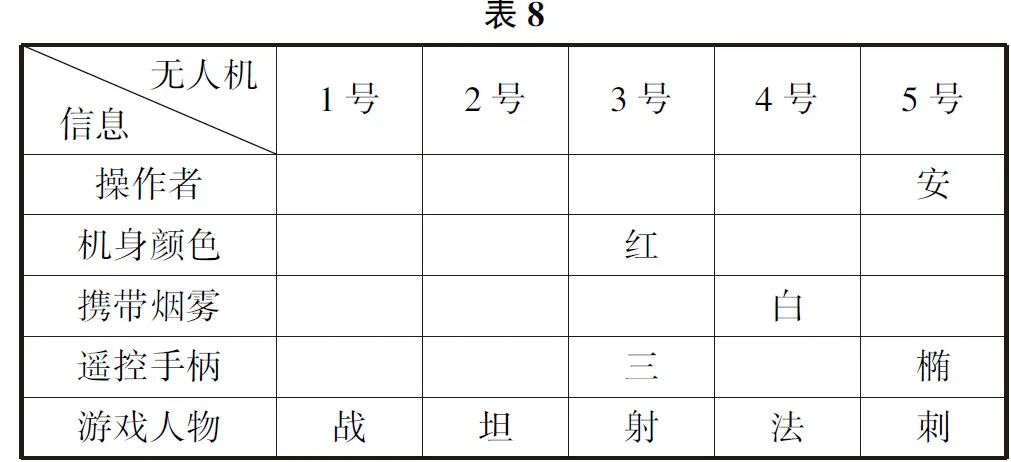
由条件7可知4号无人机的机身颜色是橙色,用梯形手柄,则对应表格为表9.

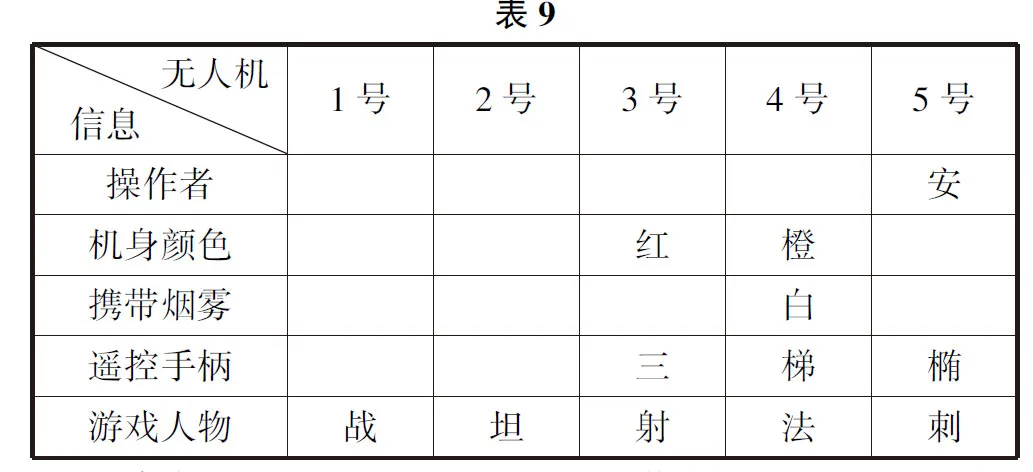
由条件8可知4号无人机的操作员是小沈,则对应表格为表10.

由条件9可知1号无人机的机身颜色为黄色,则对应表格为表11.

由条件10可知小陈操控蓝色无人机.由于4号、5号无人机的操作者已确定,1号、3号、4号无人机的机身颜色已知,所以2号无人机的机身颜色是蓝色,操作者是小陈,则对应表格为表12.

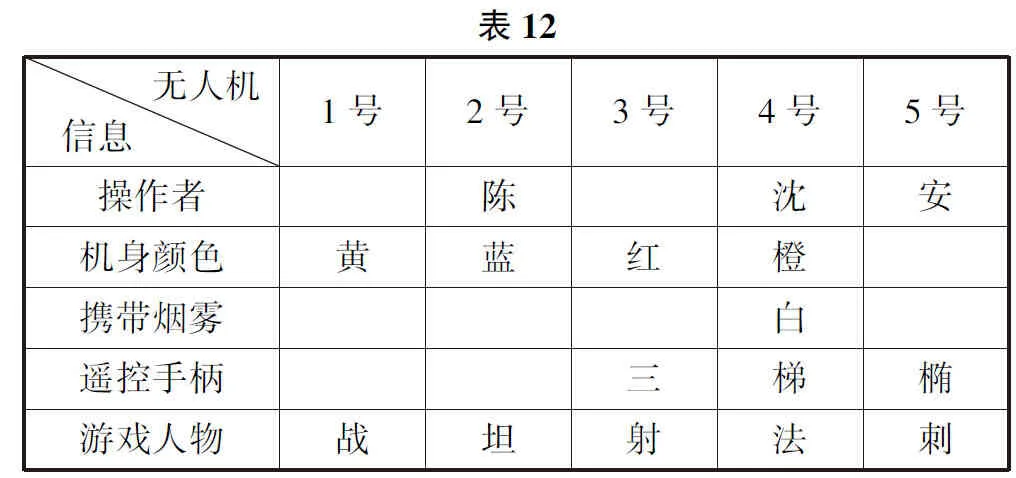
由于无人机的机身颜色有黄色、蓝色、橙色、绿色、红色,由表12可以看出5号无人机的机身颜色只能是绿色,补充表12得到表13.

由条件11可知小王使用正方形手柄.由于3号、4号、5号无人机的遥控手柄形状已确定,所以1号、2号无人机可能满足条件.但是2号无人机的操作者是小陈,所以1号无人机的操作者是小王,使用正方形手柄,则对应表格为表14.

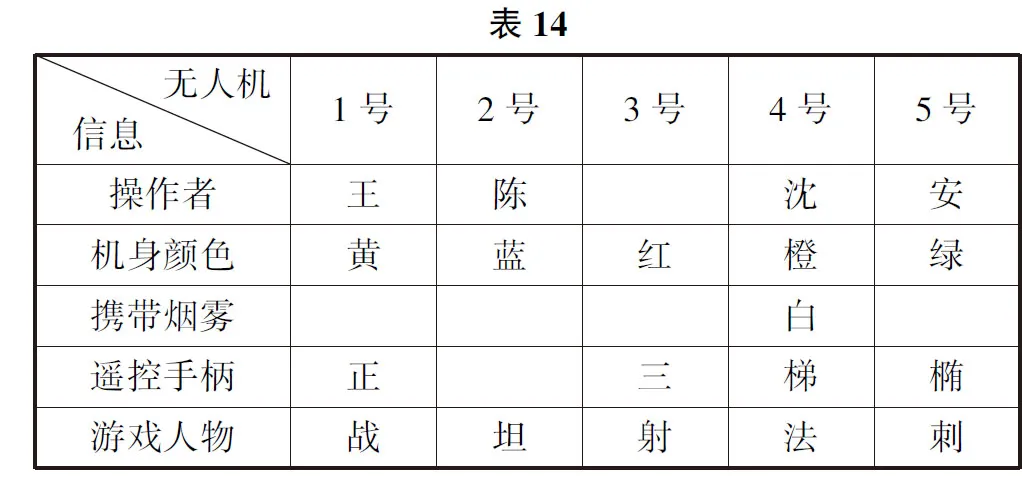
由于遥控手柄形状有正方形、椭圆形、梯形、三角形、马鞍形,由表14可以看出只有马鞍形手柄没有使用,所以2号无人机的遥控手柄是马鞍形.同理可得3号无人机的操作者是小鲁,则对应表格为表15.

由条件12可知1号无人机携带蓝色烟雾,2号无人机携带绿色烟雾,则对应表格为表16.

由条件13可知3号无人机携带红色烟雾,即5号无人机携带黄色烟雾,则对应表格为表17.

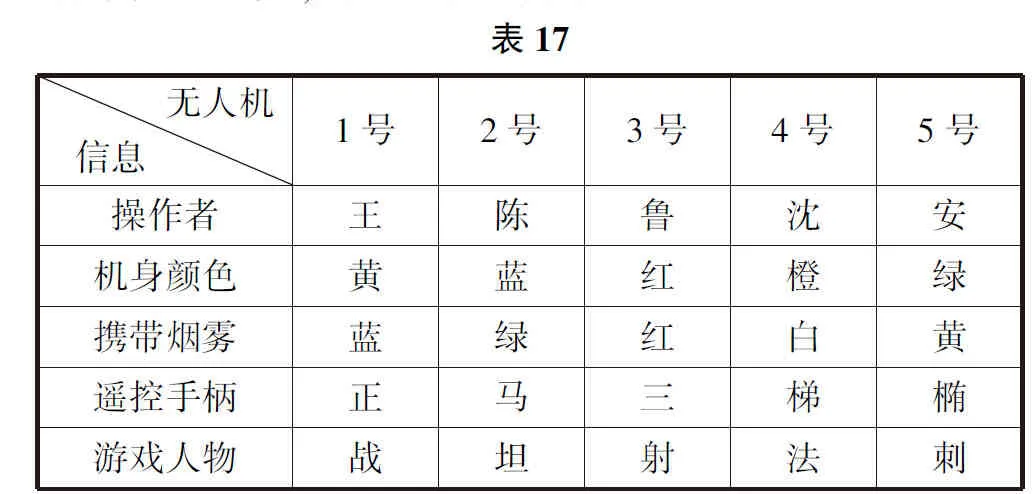
由表17可知3号无人机携带红色烟雾,小安操控的无人机携带黄色烟雾.

为了提高引例的难度,可以将其中的条件打乱顺序.

由这个问题可以发现,数表间存在联系,由彼此之间的关系可以解决较为复杂的问题,从而直接引入矩阵的定义.通过这种方法,学生感到所学知识与现实生活紧密相连,进而激发学习的积极性.

二、复习回顾,已知引新

复习回顾是对已学习内容的复习和回顾.在讲解新知识时,先对相关知识进行回顾复习,再恰当设计引出新知识,即为已知引新.复习回顾能让学生联系已学的相关知识,进而在熟悉的背景下学习新知识,这不仅能降低学生的为难情绪,也能为学生对后续内容的学习打好基础.

例如,在讲解伴随矩阵的定义时就可以使用知识回顾法.设A=(aij)是n阶方阵,Aij是|A|中元素aij的代数余子式(i,j=1,2,…,n),则称矩阵

为的伴随矩阵

先引导学生分析定义中的条件：是||中元素的代数余子式(，=1，2，…，)再提问：行列式与其元素的代数余子式有什么关系呢？进而引出：

||=11+22+…++…+

上面的等式可以用矩阵的乘法来表示，引导学生写出

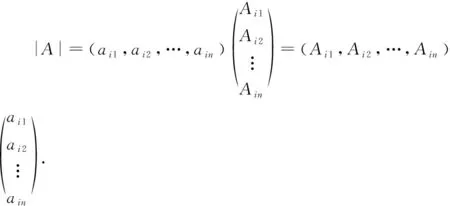
(1，2，…，)是矩阵中的第行为了与矩阵联系起来，只考虑第一个等式

结合以上知识计算：

等式右端的列矩阵中第个分量为||

由上面的等式可以计算：

一直计算，就可以得到：

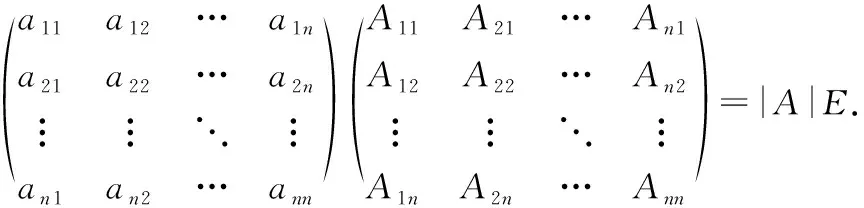
请学生仔细观察等式左端的第二个矩阵，它有什么特点？它就是伴随矩阵回顾伴随矩阵的定义，再结合上面式子讲解伴随矩阵的特点，学生理解起来会更容易之后讲解伴随矩阵的性质等，这样就能把知识融会贯通，使学生的学习变得轻松有趣