基于有限元分析和断裂准则的FOD易折杆设计*

罗俊睿，李虎山，丁子恒，王国平，方 坤，宋奎晶

（1. 合肥工业大学材料科学与工程学院，安徽合肥 230009；2. 中国电子科技集团公司第三十八研究所，安徽合肥 230088）

引 言

机场跑道异物（Foreign Object Debris, FOD）是影响机场运行安全的顽疾。据统计，全世界每年由FOD导致的事故产生超过40亿美元的维修费用，跑道安全也成为近10年我国民航运输航空最突出的问题[1-3]。2016年民航总局发布通告，将采用FOD探测系统实现FOD的防范和管理，促进了FOD探测系统的快速发展。在该背景下，本文基于有限元分析，针对力学性能要求，开展FOD探测系统易折杆结构的设计研究工作。

经分析，如果FOD易折杆为静态系统，则通过结构静载应力计算很容易实现设计要求的断裂特性。但是，因功能和环境载荷（如风、飞机尾焰等）的综合作用，FOD探测系统实际上为动态系统。因此，易折杆设计除了要满足静载断裂特性要求外[4-5]，还需满足疲劳使用寿命要求，即在疲劳载荷作用下，很难发生疲劳破坏。在材料加工领域，这两个方面的力学性能要求是矛盾的。传统易折杆设计采用V形缺口方案[6-7]，相比圆形缺口，其应力集中更严重，因此更容易满足“当断即断”的性能要求，但更严重的应力集中导致FOD易折杆使用寿命大幅下降，难以同时满足FOD系统的疲劳性能要求[8]。因此急需建立更为科学合理的FOD探测系统易折杆结构设计方法，保证系统兼具易折特性和长期使用可靠性。

1 易折杆的设计方法

1.1 易折杆的结构设计总要求

易折杆是FOD系统支撑轴的一部分，该支撑轴是底部安装基座与上部光电传感器设备的连接支撑。结合民航对机场跑道设备的要求，易折杆结构设计的主要要求包括：1）在风或航空器尾流环境下不应折断，避免自身形成飞行区FOD；2）与飞机碰撞时应立即折断，避免对飞机造成重大伤害，同时折断点不应过高，避免对轮胎造成损害，保证碰撞不会导致飞机失控。

1.2 易折杆结构设计规范

目前国内尚无FOD设备相关标准。考虑到FOD光电传感器设备与跑道边灯集成布置，其易折性具体要求可参考机场边灯要求，详见民航《AC-137-CA-2015-04 跑道和滑行道助航灯具检测规范》。根据该规范，除A型跑道警戒灯以外的立式灯具应当能承受204 N·m的弯矩而不损坏，在弯矩达到680 N·m以前应当能及时从安装系统中脱开，易折点距地面高度应小于等于38 mm。

实际上，美国已有FOD标准《FAA AC 150/5220-24 Foreign Object Debris Detection Equipment》。追溯发现，国内灯具检测规范和美国FOD检测规范的条件均来源于同一标准《FAA AC 150-5345-46 滑行道跑道灯具》，国内标准在指标上略有变化。表1列出了两种标准的对照。

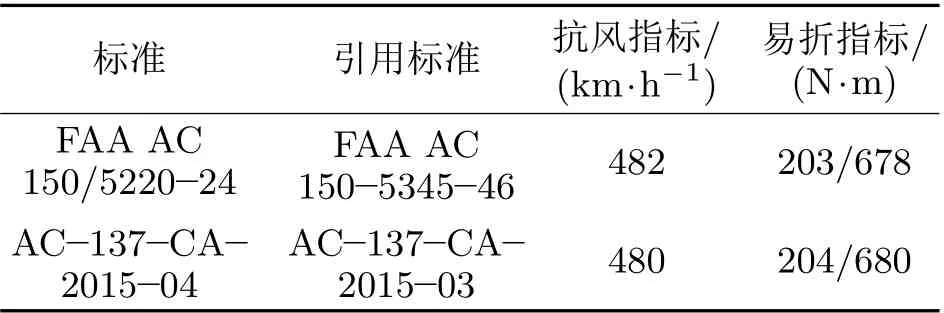
表1 易折杆设计技术要求标准

1.3 易折杆结构设计基本方案

易折结构件尺寸控制一般有两种形式：1）等径管，一般外径固定，通过控制内径来控制其壁厚尺寸；2）开槽等径管，一般采用通用的管材，在特定的高度处开槽，形成局部应力集中，通过控制切口的深度来控制其壁厚尺寸。为了控制支撑轴折断位置并降低对内径精确控制的工艺要求，采用开槽等径管对FOD光电传感器支撑轴进行结构设计，如图1所示。将易折杆设计为轴对称结构，包括上法兰、下法兰、圆管和缺口。上法兰和下法兰分别位于圆管的上方和下方，其圆周上均设有与FOD系统其他设备连接的安装孔。由易折杆的结构特点和断裂准则可知，圆管缺口设计是FOD易折杆设计的重要方面。

图1 易折杆结构示意图

易折杆圆管缺口是应力集中的位置，该位置可能在低于材料屈服应力时因结构疲劳而发生断裂，导致易折杆的使用寿命降低[5]。根据设计需求，将FOD探测系统安装在机场跑道两侧，采用步进式探测，每180°设定45个驻留探测位置，即经历45次加速和减速过程。在该过程中，易折杆承受交变扭转载荷。若FOD探测系统的设计寿命为10年，则承受交变扭转载荷的周期需超过2×108次，这显然已经超过了工程意义的疲劳寿命极限[6]。因此，FOD探测系统支架易折杆承受的交变扭转载荷不宜超过易折杆材料的扭转疲劳极限强度，否则FOD探测系统会在使用年限内发生疲劳断裂。另外，FOD探测系统的迎风面积大，距离飞机尾焰近，飞机起降过程会对其造成较大的风压弯曲载荷。目前最繁忙机场的飞机平均起飞时间为3 min一班，机场工作时间约为15 h，在设计寿命10年内，FOD探测系统累计承受风压弯曲载荷超过1×106次，因此易折杆承受的脉动弯曲载荷不能超过材料在1×106次风压载荷下的脉动疲劳强度。综上所述，FOD探测系统同时承受步进转动引起的高周扭转疲劳载荷以及飞机尾焰与系统迎风面引起的高周脉动弯曲载荷，易折杆应既具备易断性能，又具备不易疲劳失效的性能。

对于易折杆缺口，无论其形状如何，断裂前缺口尖端均会产生塑性变形，发生钝化而向圆形转变。对于疲劳断裂，缺口应力远小于材料的屈服强度，缺口处不会产生塑性变形，即不会引起缺口形状的变化，因此疲劳断裂性能对缺口形状和表面状态更加敏感，即优化缺口状态更加有利于疲劳性能的提升，从而增大设计空间。根据材料结构力学分析，相比其他类型缺口，圆形缺口的应力集中系数更小，且圆形缺口尖端在宏观和微观尺度均具有更高精度的可制造性，加工过程能够实现更高的形状精度和粗糙度，进而更能保证易折杆的疲劳性能。本文提出了在圆管上开半圆形缺口的设计方案。

1.4 外载荷的计算

根据FOD系统的迎风面积、飞机尾焰风速及受力位置，计算易折杆所受弯矩M1= 100 N·m，该载荷为脉动载荷。M1的计算式为：

式中：F为尾焰压力；L为风载作用点与缺口的距离，风载作用于支撑轴以上设备。F的计算式为：

式中：v为计算风速，v= 134 m/s；Cx为正面风阻系数，暂取值为1；A为设备迎风面积，A= 0.06 m2；ρ为空气密度，ρ= 1.226 kg/m3。134 m/s风速下，风载作用到支撑轴切口处的弯矩应不大于204 N·m，即FL ≤204 N·m，计算得到L ≤303 mm。同时考虑到整机高度不超过350 mm、支撑轴切口处离地高度不大于38 mm以及支撑轴与基座安装空间的限制，L取180 mm，则支撑轴切口处离地高度为30 mm≤38 mm，满足标准要求。

根据FOD系统的扫描角加速度及系统重量，计算易折杆所受扭矩M2= 1 N·m，该载荷为交变载荷。M2的计算式为：

式中：J为系统转动惯量，J=0.67 kg·m2；β为系统的转动角加速度，β=1.75 rad/s2。

根据表1标准确定易折杆承受的安全力矩M3=204 N·m以及断裂极限力矩M4= 680 N·m，两者均为静载荷。

1.5 易折杆材料选择及性能确定

易折杆的材料选择是实现其功能特性的关键。依据上述分析，材料选择需考虑的力学性能指标包括屈服强度σs、拉伸强度σb、脉动疲劳极限强度σ0、交变扭转疲劳极限强度σ-1和延伸率δ。由金属材料力学性能的基础规律可知：材料的屈强比（σs/σb）越小，则材料的塑性越好；材料的塑性越好，则σb/σ0越小，越有利于结构设计。因此，采用塑性较好的材料，即延伸率较高的材料，能够获得更宽的设计空间。为避免易折杆发生疲劳断裂，保证50%的安全设计空间，圆管材料的σb/σ0应不超过3.4。常用工程材料的σb/σ0数值见表2[8]。

表2 常用工程材料的σb/σ0

另外，材料的塑性好，则其较强的变形能力会使易折杆发生全面屈服，结构不断裂，容易导致易折杆在安全力矩M3=204 N·m时不发生屈服以及断裂极限力矩M4=680 N·m时发生断裂这两个限定条件下难以求解。本文采用延伸率作为判据，同时限定材料的延伸率不超过8%，能够保证设计的顺利进行。因此，所选材料的延伸率范围设计为3%～8%。查阅工程材料大典，初步确定易折杆材料为表3所列两种铝合金，其力学性能指标满足上述分析要求。

表3 铝合金的力学性能参数

1.6 易折杆特征参数及缺口尺寸的确定

易折杆圆管内径RN需根据FOD系统线缆直径确定。FOD系统线缆直径为30 mm，为了保证线缆能够顺利安装在易折杆内，选择RN为33～35 mm，后续建模采用35 mm；圆管壁厚H为2～5 mm，后续建模采用2.5 mm，由此可得外径D为40 mm；半圆形缺口半径即深度R为1～3 mm，满足0＜R ＜H，开槽后切口处外径D2=D-2R。缺口位置的确定与安全力矩M3有关。首先确定圆管与下法兰过渡圆角应力集中的影响范围至过渡圆角的最大距离X，进而确定缺口与过渡圆角之间的距离X±R。

采用数值模拟方法使大量繁杂的工程问题简单化，使复杂的过程层次化，可以避免低水平重复工作，节省大量时间，使工程分析更快、更准确，在产品的设计和分析、新产品的开发等方面发挥了重要作用[4]。以下将在易折杆材料、结构类型和尺寸基本明确的基础上，借助有限元分析和材料断裂判据，对易折杆缺口特征进行细节性设计。

2 有限元分析和断裂判据

2.1 有限元模型的建立

本文采用MSC. Marc软件进行易折杆受力的有限元分析。首先，建立易折杆的有限元网格模型。划分网格时，要使缺口附近网格的最大尺寸不超过0.01 mm，这样才能保证计算精度。其次，定义边界条件，对易折杆底部铰支，在上端面分别施加弯矩载荷M1、扭矩载荷M2、安全力矩M3和断裂极限力矩M4。M1，M2，M3和M4的具体数值见1.4 节。然后，设置材料性能参数，包括密度、弹性模量、泊松比以及力学本构关系。本文采用幂指数硬化方程描述铝合金的变形行为。在施加M1，M2和M3时，定义应力σ= 0.9(σs+mεn)，施加M4时，定义σ= 1.12(σs+mεn)，其中ε为等效塑性应变，常数m和n通过拟合材料的室温拉伸应力应变曲线近似获得。对于2A14铝合金，取m= 115,n= 0.37。对于7A09铝合金，取m= 247,n= 0.38。最后，定义计算工况，提交计算任务后，即可进行后处理分析。

2.2 断裂判据

基于以上有限元模型，计算M1，M2，M3和M4四种状态下易折杆缺口处的应力应变状态，获得M1，M2和M3对应的缺口最大应力σ1，σ2和σ3以及M4对应的缺口等效塑性应变ε1。易折杆设计需满足以下两个断裂判据：

1）σ1≤σ0,σ2≤σ-1,σ3≤σs，保证易折杆在服役期内不会发生疲劳断裂；

2）ε ≥δ，保证FOD与探测系统发生撞击时，易折杆快速断开。

2.3 不同易折杆几何特征参数的数值模拟

以H,R以及缺口形状为自变量，以σ1，σ2，σ3和ε为目标量，进行三因素的数值模拟。易折杆特征参数如表4所示。

表4 易折杆的特征参数

基于表中几组参数，对易折杆受力进行建模分析。首先确定易折杆缺口位置，方法如下：在安全力矩M3的有限元模型计算结果中，提取圆管与下法兰过渡圆角最大应力处圆管轴线方向的应力分布曲线。由曲线确定应力与距离呈非线性关系的区域，即圆管与下法兰过渡圆角应力集中的影响范围，确定该范围与过渡圆角的最大距离X。第1,2,5组易折杆材料选择2Al4铝合金，曲线如图2所示。根据数据处理结果，确定X=22 mm，缺口与过渡圆角的距离为21 mm。第3,4组易折杆材料选择7A09铝合金，曲线如图3所示，同理确定X=18 mm，缺口与过渡圆角的距离分别为19.5 mm和19.3 mm。

图2 圆管与下法兰过渡圆角最大应力处圆管轴线方向的应力分布曲线（易折杆材料选择2A14铝合金）

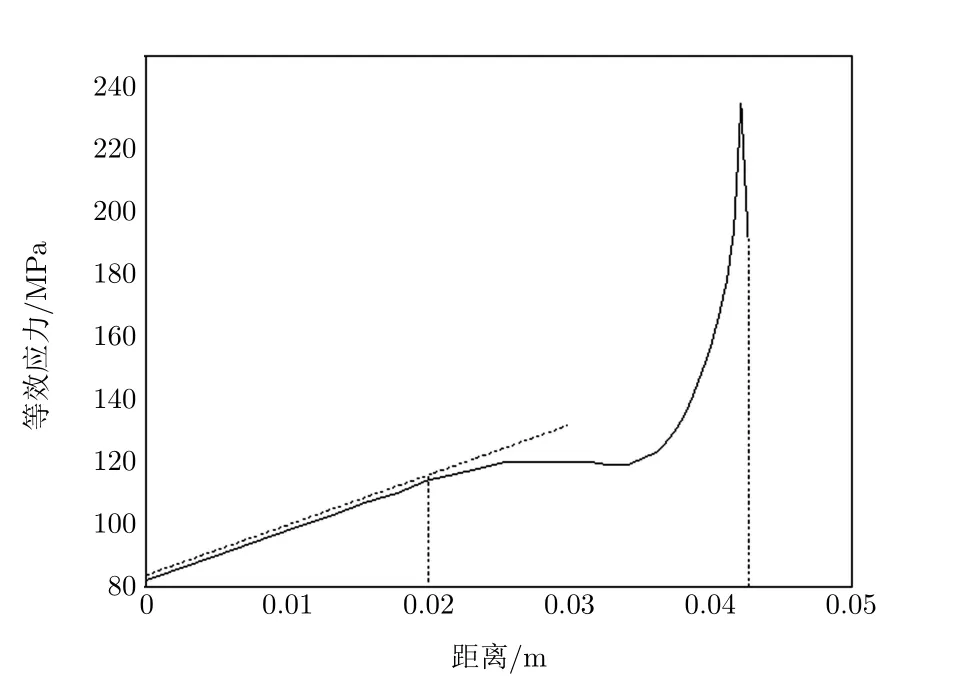
图3 圆管与下法兰过渡圆角最大应力处圆管轴线方向的应力分布曲线（易折杆材料选择7A09铝合金）

采用第1组特征参数，得到σ1= 50 MPa, σ2=0.9 MPa, σ3= 103 MPa, ε= 0.000 05。经过与两条断裂判据作比较，发现σ1≤σ0= 155 MPa, σ2≤σ-1=124 MPa, σ3≤σs= 320 MPa, ε ≤δ=4%，即判据1满足而判据2不满足，则易折杆在FOD碰撞时难以折断。因此，需将易折杆R值增大或H值减小。

第1组特征参数下易折杆缺口处4种状态下的应力、应变云图如图4所示。

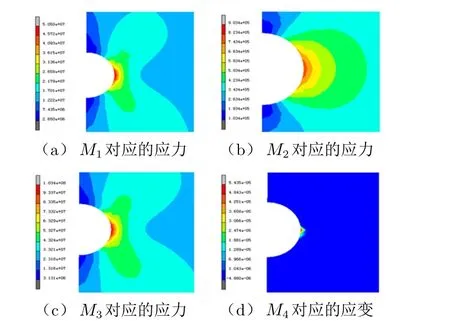
图4 第1组特征参数下易折杆缺口处的应力、应变模拟结果

采用第2组特征参数，得到σ1= 147 MPa, σ2=1.8 MPa, σ3= 294 MPa, ε= 0.042。σ1≤σ0=155 MPa, σ2≤ σ-1= 124 MPa, σ3≤ σs=320 MPa, ε ≥δ= 4%，满足两个断裂判据，因此，第2组参数的设计合理。

第2组特征参数下易折杆缺口处4种状态下的应力、应变云图如图5所示。

图5 第2组特征参数下易折杆缺口处的应力、应变模拟结果

采用第3组特征参数，得到σ1= 252 MPa, σ2=2.2 MPa, σ3= 508 MPa, ε= 0.11。σ1≤σ0=220 MPa, σ2≤ σ-1= 175 MPa, σ3≥ σs=420 MPa, ε ≥δ= 7%，即判据1不满足而判据2满足，这将导致易折杆在设计使用寿命达到前发生疲劳断裂或发生变形而影响探测精度。因此，需将易折杆R值减小或H值增大。

采用第4组特征参数，得到σ1= 204 MPa, σ2=1.9 MPa, σ3= 411 MPa, ε= 0.083，即σ1≤σ0=220 MPa, σ2≤ σ-1= 175 MPa, σ3≥ σs=420 MPa, ε ≥δ= 7%，满足两个断裂判据，因此，第4组参数的设计合理。

综上所述，将易折杆缺口设计为圆形能够同时实现易折特性和长期使用可靠性。第5组参数采用了V形缺口设计，得出σ1= 316 MPa，超出了材料的脉动疲劳极限σ0。M4对应的ε=0.18，即ε ≥δ，撞击时可以发生断裂，但易折杆的使用寿命不满足设计要求。

σ0和疲劳寿命N的关系为σ0=CNh，其中C和h为常数。对于铝合金，h约为0.2。

相同条件下，半圆形缺口的疲劳寿命NR和V形缺口的疲劳寿命NV之间的关系为=2%，由此可知，V形缺口易折杆的疲劳寿命比半圆形缺口缩短了98%。

3 结束语

本文完整地给出了机场FOD探测系统易折杆的结构设计方案，包括载荷计算方法、材料综合力学性能选择的判定依据、基于有限元的承载应力应变数值分析方法以及当断则断和疲劳可靠性的力学判据，完成了FOD探测系统研发工作的重要一环。

根据有限元分析得出，采用圆形缺口设计具有更大的灵活性，可通过缺口尺寸的调整来满足系统设计要求。当结构设计不满足σ1≤σ0,σ2≤σ-1,σ3≤σs的合格判据时，需要增大圆管壁厚值或者减小缺口半径值；当ε ≤δ，不满足合格判据时，需要增大缺口半径值或者减小圆管壁厚值。相比传统V形缺口设计，圆形缺口设计可以大大提高易折杆的疲劳寿命。