灰色-小波神经网络在高层建筑物沉降预测中的应用

付 伟，白洪伟，董 杰，赵 强

(宿州学院 环境与测绘工程学院，安徽 宿州 234000)

高层建筑物受地质、负载、施工等因素的影响必然会出现沉降现象，当沉降达到一定量后会严重影响建筑物建设及使用安全，严重威胁人们的生命财产安全[1]。为保障建筑物的安全建设与正常运营，人们对高层建筑物沉降监测和预报的研究越来越重视[2]。现阶段常用于沉降预测的模型主要包括回归分析、时间序列、Kalman滤波、灰色系统、神经网络等[3](P92)。在工程实践中，人们往往会选择两种或多种模型进行组合，实现较高的预测精度。陈盟，姜刚等利用卡尔曼滤波结合灰色理论模型对地铁沉降进行预测，得出组合模型在一定程度上可提高预测值精度[4]。夏磊凯等将灰色模型和BP神经网络组合对基坑沉降进行分析，得出了组合模型具有预测精度高、适用于短期建模的结论[5]。姜刚等利用灰色-小波网络模型对地铁基坑地表沉降进行拟合，得出组合模型预测结果稳定且比单模型准确度高的结论[6]。杨学超等将小波去噪与POS-BP神经网络组合，对跨海大桥变形数据进行预测，得出组合模型预测精度较高的结论[7]。本文利用滑动GM(1,1)模型优化GM(1,1)模型建模时随序列的增长预测精度较差、易发散的问题，重点研究分析了滑动GM(1,1)与小波神经网络组合模型的预测精度。

1 灰色模型

1.1 GM(1,1)灰色模型

灰色模型是对原始数据进行处理，弱化其随机性，具有所需建模数据少、能够保持系统的原有特征、能很好地反映系统的实际情况等优点[6]。GM(1,1)是最常用的一种灰色模型，其建模过程如下[8]：

(1)在原始数据基础上构建累加序列。设原始数据序列如下：x(0)={x(0)(1),x(0)(2),…x(0)(n)}，x(0)(k)≥0,k=1,2,…n。对x(0)进行累加生成新序列x(1)={x(1)(1),x(1)(2),…x(1)(n)}。其中，

(1)

(2)生成紧邻均值序列。

(2)

(3)构建模型。利用x(1)构成一阶微分方程：

(3)

式中，a为发展系数，u为灰色作用。

(4)解微分方程。

(4)

式中B与Y如下所示：

将x(0)(1)=x(1)(1)作为初始值，带入式(5)可求得微分方程的解：

(5)

(5)生成预测方程：

(6)

1.2 滑动GM(1,1)模型

1.3 模型精度评定

本文采用绝对误差、相对误差及平均相对误差对建模精度进行评定[4]。

(1)绝对误差序列：e(0)={e(0)(1),e(0)(2),…e(0)(n)}，其中

(7)

(2)相对误差序列：q={q1,q2,…，qn}，其中

(8)

2 小波神经网络

小波神经网络是在BP神经网络的基础上，利用小波基函数(Morlet)代替BP神经网络隐含层的激励函数，作为隐含层节点的传递函数[9]，其表达为：

(9)

小波神经网络根据误差反向传播的学习算法进行网络学习训练，使网络拥有更加高效的收敛能力和更优的拟合能力。网络由输入层、隐含层和输出层组成，其结构如图1，图中xI为输入向量，m为输入层节点数，Wij为输入层与隐含层之间的权值，s为隐含层节点数，hj为隐含层输出值，Wjk为隐含层与输出层之间的权值，n为输出层节点数，yk为网络的输出[10]。

图1 小波神经网络结构

网络中设netj为第j个隐含层的输入值，其表达式如下：

(10)

式中，Wij为第i个输入层和隐含层节点的权值，xi为输入向量。

结合Morlet小波基函数则隐含层输入表达式如下：

(11)

式中，h(j)为第j个隐含层神经元的输出值；hj为Morlet小波基函数，aj、bj为其伸缩与平移因子。

小波神经网络输出层的输出表达式为：

(12)

3 实验分析

3.1 数据预处理

为验证模型的预测效果，本文以某城市国色天香小区2号楼32层建筑物为研究对象。该建筑物采用二等水准进行沉降观测，选取了监测点C202和C206的18期观测数据进行建模预测与分析，其中前12期为样本，后6期做为预测数据。由于在观测数据中既包含所需的沉降信息也包含各类噪声，这些噪声迭加在一起，会使得形成的观测曲线呈现异常的波动[3](p82)。为了消除或削弱观测噪声对模型精度的影响，本文采用二次函数平滑法对观测数据进行预处理，二次函数平滑表达式如下：

L=a0+a1T+a2T2

(13)

式中，L为观测值序列，L=(L1,L2,…,Ln)；T为观测周期序列，T=(T1,T2,…,Tn)；a0、a1、a2为待求参数。

3.2 灰色-小波神经网络模型

由于GM(1,1)有对长序列预测时易发且散残差大等缺点，本文采用滑动GM(1,1)和小波神经网络组合起来建立预测模型以提高预测精度，其建立与实现方法如下：

(1)整理观测数据进行数据预处理得到去噪数据。

(2)利用去噪数据建立滑动GM(1,1)模型进行拟合。

(3)用去噪数据减去拟合数据得差值序列。

(4)利用MATLAB软件构建小波神经网络模型。以差值序列为网络输入据进行学习训，网络输出为待预测沉降的滑动GM(1,1)期望差值。经实验分析确定小波神经网络模型为3层网络：输入层2个节点、隐含层12个节点、输出层1个节点。训练前将差值序列进行归一化处理，利用所建网络进行训练。为得到有效预测结果，本文将训练样本分为6组，每组样本12个数据，即第1组是第1期到第12期的观测值与滑动GM(1,1)拟合值差值，第13期为输出值；第2组是第2期到第13期的观测值与滑动GM(1,1)拟合值差值，第14期为输出值；第3组为第3期到14期的观测值与滑动GM(1,1)拟合值差值，依次类推预测13期到18期数据。

(5)构建组合模型进行沉降预测与分析。

经各模型数据处理得到表1监测点C202和表2监测点C206预测结果数据。可得GM(1,1)模型在两监测点各期预测残差随着预测期数的增多残差明显增大，其范围为-6.1410～1.2162 mm；监测点C202、C206残差平均值分别为-3.1189 mm和-3.4496 mm，监测点各期综合残差平均值为-3.2843 mm；两监测点残差的标准差为分别为1.6560和1.8225。滑动GM(1,1)模型两监测点各期预测残差范围为-1.6940～-0.3811 mm，两监测点残差平均值分别为-0.8089 mm和-0.9361 mm，监测点各期综合残差平均值为-0.8725 mm；两监测点残差的标准差为分别为0.4180 mm和0.4890 mm。灰色-小波神经网络模型两监测点各期预测残差范围为-0.2197～0.0561 mm mm，两监测点残差平均值分别为-0.0320 mm和-0.0529 mm，监测点各期综合残差平均值为-0.0425 mm；两监测点残差的标准差为分别为0.0501 mm和0.1003 mm。综上GM(1,1)模型各期预测残差最大、稳定性较差；滑动GM(1,1)模型预测残差相对较小、稳定性相对较好；灰色-小波神经网络模型预测残差最小、稳定性最好。说明了滑动GM(1,1)模型可以很好地优化GM(1,1)模型，灰色-小波神经网络模型又能够更进一步优化滑动GM(1,1)模型且精度较高。

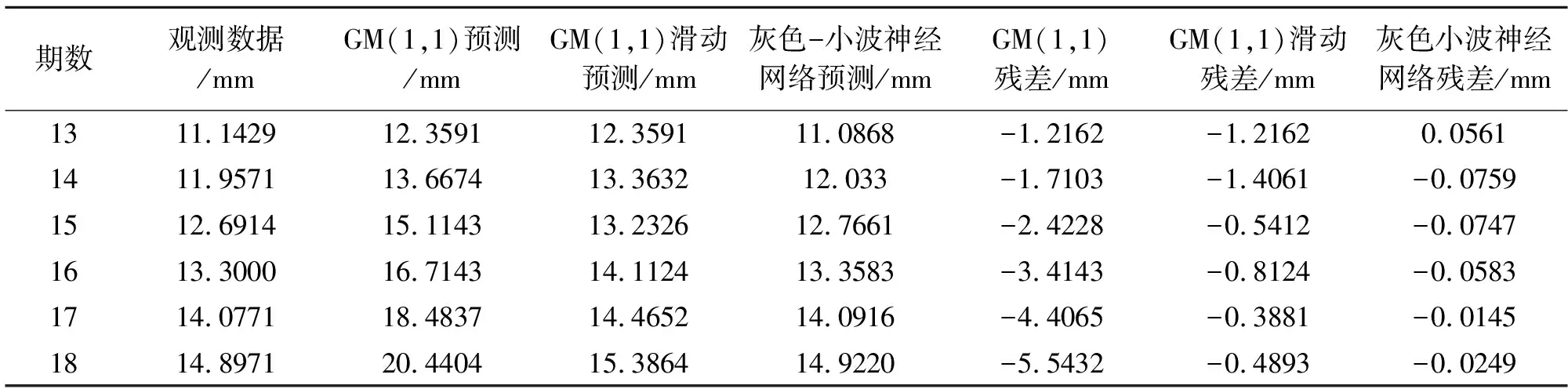
表1 监测点C202不同模型预测结果数据

表2 监测点C206不同模型处理结果数据

为进一步对比GM(1,1)、滑动GM(1,1)与组合模型预测效果，图2、3为监测点C202和C206观测值与各模型预测值对比图，可知灰色-小波神经网络模型各期预测结果与观测值更接近。

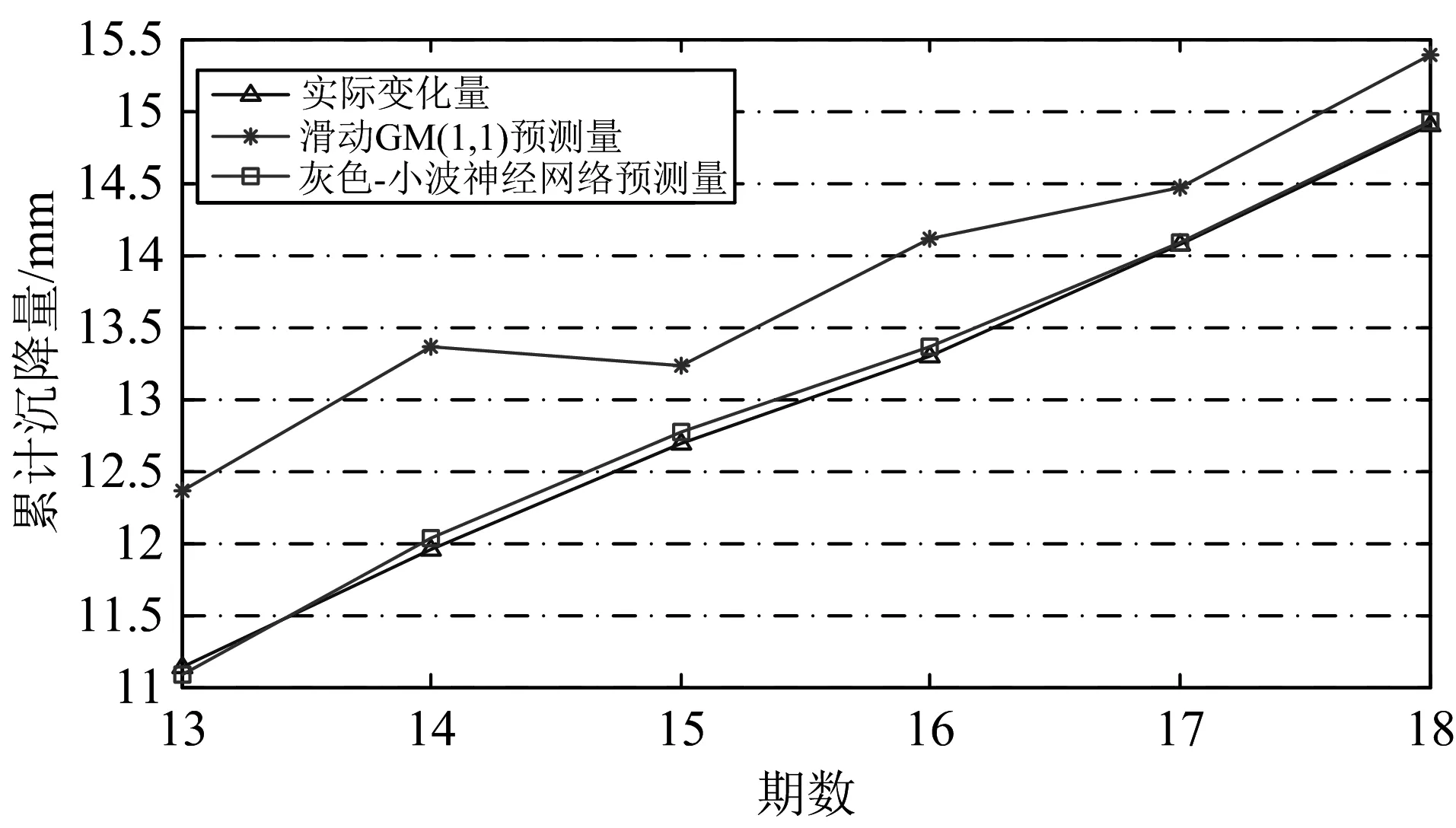
图2 监测点C202 不同模型处理数据对比

图3 监测点C206 不同模型处理数据对比

图4、5为监测点C202和C206观测值与各模型预测值残差对比。可知组合模型残差值均小于滑动GM(1,1)模型残差且比滑动GM(1,1)模型更稳定，即组合模型预测效果优于滑动GM(1,1)模型。

图4 点C202 不同模型预测值残差对比

图5 点C206 不同模型预测值残差对比

为分析滑动GM(1,1)与灰色-小波神经网络模型的预测精度，表3为两个监测点滑动GM(1,1)与灰色-小波神经网络模型预测值与观测值的相对误差。可知滑动GM(1,1)模型预测各监测点各期相对误差范围为-14.71%～2.76%，两监测点平均相对误差分别是-6.51%和-9.23%，监测点综合平均相对误差为-7.87%。灰色-小波神经网络预测各监测点各期相对误差范围为-1.68%～0.50%，两监测点平均相对误差分别为-0.24%和-0.44%，监测点综合平均相对误差为-0.34%。组合模型比滑动GM(1,1)模型相对误差在两监测点分别减小了5.91%、8.79%，综合平均相对误差减小了7.53%。故从相对误差分析可得灰色-小波神经网络相对于滑动GM(1,1)模型有很好的预测结果。

表3 点C206不同模型相对误差表

图6、7为监测点C202、C206观测值与两模型预测值相对误差对比图。可知组合模型相对误差均小于滑动GM(1,1)的残差且更稳定并趋于0，说明组合模型预测精度较高。

图6 点C202 不同模型相对误差对比

图7 点C206 不同模型相对误差对比

综上分析，GM(1,1)模型对高层建筑物沉降预测误差相对较大且随期数增加残差增大明显；滑动GM(1,1)模型能够很好地优化GM(1,1)模型；灰色-小波组合模型可以进一步优化滑动GM(1,1)模型且具有较高的预测精度。

4 结论

本文对比验证分析了GM(1,1)、滑动GM(1,1)和灰色-小波神经网络模型在高层建筑物沉降监测中预测的应用。以国色天香小区32层高层建筑物监测点C202和C206观测的18期数据为依据，构建了GM(1,1)、滑动GM(1,1)和灰色-小波神经网络模型，对比分析了各模型的预测残差和相对误差，重点分析了滑动GM(1,1)和灰色-小波神经网络模型预测精度。结果表明，滑动GM(1,1)模型在能够很好地优化GM(1,1)模型；灰色-小波神经网络组合模型能够进一步优化滑动GM(1,1)模型且具有较高的预测精度。