二进制动力系统中乘积型动力丢番图逼近问题研究
2022-10-26王修建
李 露,王修建,岳 芹
(皖西学院 金融与数学学院,安徽 六安 237012)
经典的丢番图逼近是数论的一个分支,它主要研究有理数逼近无理数的精度问题。换句话说,对任意小的正数ε>0以及任意的实数x∈R,总存在一个有理数p/q∈Q,使得|x-p/q|<ε。这也说明,任何实数都可以被有理数很好地逼近。动力丢番图逼近最近受到广泛关注,它主要在动力系统下定量地研究点的轨道的分布,让我们更好地理解点的轨道的丢番图性质。设(X,T,μ)是一个测度动力系统,T:X→X是一个变换,μ是一个T-不变的测度,由Poincaré 常返定理可知:对任意的x0∈X以及μ-几乎处处的x∈X,有
本质上这只是一个定性的结果,上式并没有清楚地表明点x的轨道将以何种速度返回到初始点x0。更精确的说,设T:X→X是一个变换,φ:N→R+是一个正函数,任意的
x0∈X
我们想知道以下集合
{x∈X:|Tnx-x0|<φ(n)对无穷对个n∈N成立}
的度量性质。
1967年,Philipp首次证明了上述集合的Lebesgue测度满足0-1律[1];1995年,Hill和Velani给出了该集合的Hausdorff维数结果[2]。随后,大量的学者开始积极地研究动力丢番图逼近相关问题,如动力Borel-Cantelli引理[3,4]、首次返回时间[5]、收缩靶问题等[6,7]。
一维的动力丢番图逼近问题的度量理论已经得到了完整的刻画,然而,对于高维情况,这方面的结果相对较少。本文主要研究二进制动力系统中二维的乘积型丢番图逼近问题,给出了相应集合Hausdorff测度的刻画。
1 研究内容
首先介绍二进制展式的概念,然后介绍本文所研究的问题,最后给出本文的结果。对任意的x∈[0,1),令
T2x=2x-⎣2x」
其中,⎣ξ」表示不超过ξ的最大整数。我们取
εn(x)=⎣2T2n-1x」∈N
则任意的x∈[0,1)可以唯一地展成如下形式:
(1)
称(1)式为二进制展式,这个系统([0,1),T2)被称为二进制动力系统。很明显,任意的k≥1,εk(x)∈{0,1}.
本文主要研究二进制展式中的乘积型动力丢番图逼近问题,具体地说:设φ:N→R+是一个正函数,任意的x0,y0∈[0,1),定义集合
本文证明了集合M2(T2,φ)的Hausdorff测度如下:
定理设φ:N→R+是一个正函数。则对任意的正实数s,且1 其中,Hs(·)表示为s-维的Hausdorff测度。 本节主要介绍所需的基础知识。首先引入Hausdorff测度的概念和性质,然后介绍二进制展式的一些基本性质,最后介绍后面证明所需的两个引理。 设X是一个度量空间,U是X的非空子集,定义U的直径为: |U|∶=sup{|x-y|:x,y∈U} 设E⊆X且δ>0,如果集合E可以被直径不超过δ的可数集族{Ui}i≥1覆盖,即任意的正整数i≥1,有 则称{Ui}i≥1是集合E的一个δ-覆盖。 设E⊆X,s>0,定义 其中,inf表示对E的所有δ-覆盖取下确界。显然,对任意0<δ1<δ2, 且Hs(E)被称之为集合E的s-维的Hausdorff测度。 对任意的正整数n≥1,令 Σn∶={(ε1,…,εn)∈Nn:εk∈{0,1},1≤k≤n}. 因此 #Σn=2n (2) 其中,#表示集合元素的个数。 对任意的(ε1,…,εn)∈Σn,我们定义它的n-阶柱集如下: In(ε1,…,εn)∶={x∈[0,1):εi(x)=εi,1≤i≤n}. 我们可以得到 是长度为1/2n的区间。 根据n-阶柱集的定义,{In(ε1,…,εn):(ε1,…,εn)∈Σn}是[0,1)的一个划分,即 (3) 任意的u=(ε1,…,εn)∈Σn,令 对任意的x∈In(ε1,…,εn),根据x的二进制展式: 我们可得 (4) 下面这个覆盖引理是由Bovey和Dodson[8]证明的,它在证明定理的收敛部分起到关键的作用。 引理1(覆盖引理)设r是任意小的正数,对任意的正实数s,且1 {(x,y)∈[0,1)2:xy 存在由正方体组成的覆盖{Ui}i≥1,且满足: 本文定理的证明将被分成两部分:收敛部分和发散部分。 该部分的证明是主要找到M2(T2,φ)的一个“经济”的覆盖。根据上限集的定义以及公式(2),有 (5) 由公式(4)知,任意的(x,y)∈M2(u,v),存在一个正方形U∈{Ui}i≥1,使得 如果令正方形 U∶=[a,a+|U|]×[b,b+|U|] (其中a,b为任意实数) 则 从而 Hs(M2(T2,φ))=0 发散部分的证明需要利用Coons, Hussain和Wang[9]一维情形的结果。对任意的x0∈[0,1),定义集合 2016年,Coons, Hussain 和Wang证明了该集合的Hausdorff测度,具体内容如下: 设φ:N→R+是一个正函数。则对任意的正实数t,且0 因为 M1(T2,φ)×[0,1)⊆M2(T2,φ) 当1 Hs(M2(T2,φ))≥Ht(M1(T2,φ))=∞ 从而 Hs(M2(T2,φ))=∞ 本文主要刻画了二进制动力系统中二维的乘积型丢番图逼近问题的度量性质。设([0,1],T2)是二进制动力系统,设φ:N→R+是一个正函数,任意的x0,y0∈[0,1),定义集合 对任意的正实数s,且12 预备知识
2.1 Hausdorff测度
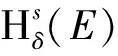
2.2 二进制展式的基本性质
2.3 覆盖引理
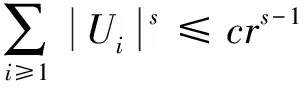
3 定理的证明
3.1 收敛部分的证明



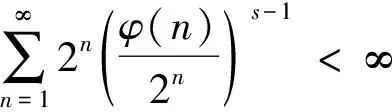
3.2 发散部分的证明

4 结论
