基于BP-ANN的贯流泵装置能量性能参数的预测及分析

2022-10-26沈强儒吕玉婷陆美凝蒋东进

水资源与水工程学报 2022年5期

沈强儒，吕玉婷，陆美凝，蒋东进，杨帆

(1.南通大学交通与土木工程学院，江苏南通 226019；2.扬州大学水利科学与工程学院，江苏扬州 225009；3.江苏省洪泽湖水利工程管理处，江苏淮安 223005 )

1 研究背景

叶片泵常用变速调节和变角调节两种方式，其中变速调节可实时调节水泵的运行工况，确保水泵高效、经济合理地运行，对同台泵装置的性能换算采用水泵比例律公式进行不同转速泵装置的能量性能计算，但水泵比例律公式的应用受到泵的大小和转速等条件限制。不同转速时泵装置的能量性能换算要求将泵内的液体运动作严格的数学求解，但求解非常困难，至今从理论分析角度尚未解决。

对于不同转速时水泵及泵装置的水力性能，国内外已开展了相关的研究工作，并取得了一些成果[1-14]，研究内容主要集中于不同转速对泵的叶片压力、进出口速度环量、轴向力等水力性能参数和叶顶间隙泄漏涡影响的数值分析[1-4]方面，以及不同转速时泵能量性能变化规律的试验分析[5-6]、不同转速对泵装置出水流道水力损失及内流场影响的数值分析[7-9]、不同智能算法对泵能量性能的预测[10-12]等方面，对泵及泵装置能量性能参数预测的研究主要集中于定转速不同叶片安放角的泵能量性能的预测，而对不同转速时泵装置能量性能的预测鲜见报道。为解决转速变化超过20%时贯流泵装置能量性能参数预测的准确性问题，本文基于贯流泵装置物理模型试验数据，构建了不同转速时贯流泵装置能量性能预测的BP神经网络模型，并通过物理模型试验数据进行了验证。

2 能量性能试验装置

2.1 贯流泵装置模型

贯流泵装置包括直管式进水流道、叶轮、导叶体、S形弯管及直管式出水流道等部分，各过流结构的参数在文献[8]、[9]中均有介绍，本文不再赘述，贯流泵装置物理模型如图1所示。

2.2 试验台及试验内容

物理试验在江苏省高等学校重点实验室的高精度水力机械试验台上进行，该试验台综合不确定度满足文献[15]的规定要求，该试验台的相关参数在文献[16]中有详细介绍，本文不再赘述。贯流泵装置能量性能试验按照文献[15]中6.1节能量试验要求进行测试，以转速1 450 r/min为基准，在1 450 r/min时采集贯流泵装置能量性能15组数据，随后进行5组不同转速(1 215、1 080、945、877和811 r/min)时泵装置能量性能测试，每组采集7个工况点数据。

3 试验结果与分析

不同转速时贯流泵装置的扬程-流量曲线和效率-流量曲线如图2所示。

图2 不同转速时泵装置的扬程-流量曲线和效率-流量曲线

由图2(a)可知，不同转速时，贯流泵装置的扬程-流量曲线的变化趋势大致相同；随着转速的增加，扬程-流量曲线的正切斜率越来越大；当转速变化较大时，不同转速的泵装置扬程-流量曲线已不满足水泵相似律换算关系，因水体黏性等因素的影响，泵内水流的运动和动力条件已不满足相似关系，严格理论意义上的运动相似是一种理论抽象的结果。图2(b)表明，随着叶轮转速的增加，贯流泵装置的最优工况点向大流量方向偏移，最高效率略有增加。

依据贯流泵的基本方程，相同流量时，随着转速的增加，叶轮出口的圆周速度增大，绝对速度的圆周分量增大，贯流泵的扬程增大，贯流泵装置的扬程也增大。在不计阻力损失的条件下，叶轮的轴功率全部传给水体，随着转速的增加叶轮的轴功率也增大，图2中的试验数据表明随着转速的增大，泵装置的最优工况效率也有所增加。在叶轮转速变化范围较大时，若采用水泵相似律对不同转速贯流泵装置进行能量性能参数换算必然会使试验结果与换算结果存在一定偏差。

根据文献[17]中水泵的相似律和比转速ns计算式可得：

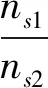
(1)

式中：n为叶轮的转速，r/min；ns为水泵的比转速；Q为水泵的流量，m3/s；H为水泵的扬程，m；下标1、2表示叶轮的两个转速。

由公式(1)推导可知，当叶轮转速变化时，水泵的比转速为定值，不同转速时最优工况模型泵装置的能量性能参数如表1所示。在转速变化未超过200 r/min时，水泵的比转速是相等的；转速在877～1 450 r/min范围内经最优工况贯流泵装置能量性能参数计算所得的叶轮比转速不是定值，随着叶轮转速的增加，叶轮的比转速呈先增大后减小的变化趋势，表明水泵的相似律计算式适用于叶轮转速变化不大的范围内。

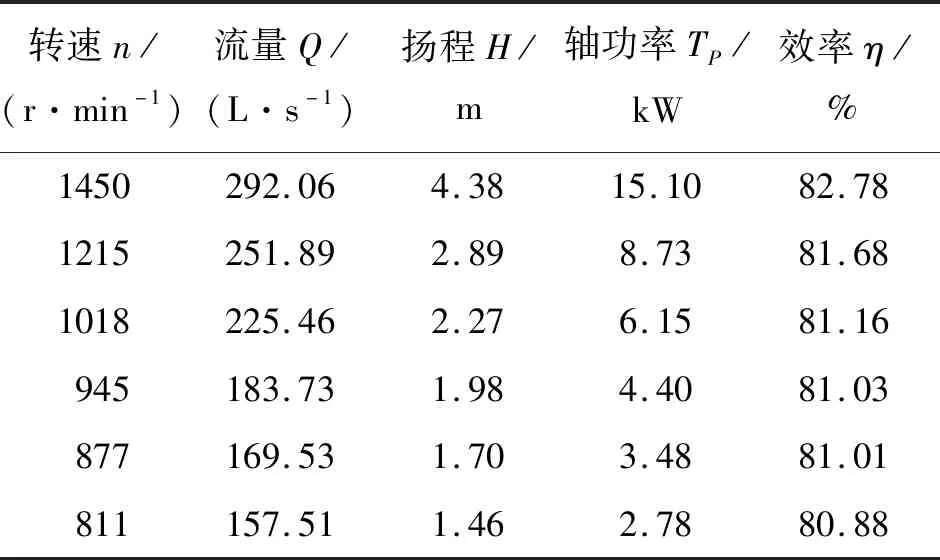
表1 不同转速泵装置最优工况性能参数

为进一步揭示不同转速时贯流泵装置的叶轮比转速不相等的内在原因，假定泵装置的扬程为Hs，泵叶轮的扬程为Hp，泵的水力损失为Δhp，进水流道的水力损失为Δhj，出水流道的水力损失为Δhc，则泵装置的扬程Hs的计算式可表示为：

Hs=Hp-Δhp-Δhj-Δhc

(2)

式中：Hs为泵装置的扬程，m；Hp为泵叶轮的扬程，m；Δhp为泵的水力损失，m；Δhj为进水流道的水力损失，m；Δhc为出水流道的水力损失，m。

不同转速时泵装置扬程之比可表示为：

(3)

式中：Hs1、Hs2为不同转速时泵装置的扬程，m；Hp1、Hp2为不同转速时泵叶轮的扬程，m；Δhp1、Δhp2为不同转速时泵的水力损失，m；Δhj1、Δhj2为不同转速时进水流道的水力损失，m；Δhc1、Δhc2为不同转速时出水流道的水力损失，m。

在不考虑小流量工况泵装置运行时，泵的扬程与流量满足二次方关系，泵装置进水流道的水力损失与流量满足二次方关系[18]，出水流道的水力损失与流量不满足二次方关系[19-20]，将公式(3)改写为：

(4)

式中：K1、K2为不同转速时泵的扬程与流量的换算系数；S1、S2为不同转速时进水流道和泵的水力损失换算系数之和；Q1、Q2为不同转速时水泵的流量，m3/s。

不同转速时泵的扬程-流量曲线近似平行，泵的扬程与流量换算系数K1与K2近似相等；在不考虑小流量工况时进水流道的水力损失系数与流道的几何边界条件相关，与叶轮转速无关，故不同转速时进水流道的水力损失系数相等；出水流道的水力损失与流量不满足二次方关系，则不同转速时泵装置扬程的比值关系如下：

(5)

式中：n1、n2为水泵的不同转速，r/min。

当叶轮转速变化较大时，出水流道内部流态受导叶体出口剩余环量的影响较大从而对贯流泵装置扬程的影响较为明显。对不同转速的贯流泵装置能量性能参数进行换算时，由于叶轮所受的阻力矩不满足相似关系，叶轮的轴功率也不满足相似关系，则采用泵装置效率换算时，必然导致泵装置效率值存在一定的偏差。

通过上述的试验结果及理论计算式推导分析可知，若转速变化较大时，采用相似律换算泵装置能量性能将导致换算结果存在较大误差，为解决该问题，本文提出了一种基于BP-ANN(back-propagation artificial neural network)模型的不同转速泵装置能量性能参数的预测方法。

4 BP-ANN预测模型的构建

4.1 网络结构

基于BP-ANN的不同转速贯流泵装置能量性能参数预测模型选用3层网络结构，网络结构由输入层神经元数、隐含层节点数和神经元数目组成，其中输入层神经元数目为样本指标数，隐含层节点数需在实际计算中反复训练[21]。BP-ANN神经网络结构如图3所示。

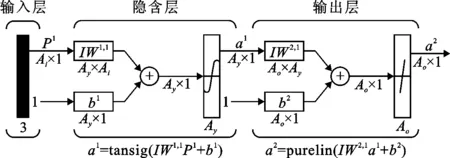
图3 BP-ANN网络结构示意图

针对实际泵站装置运行时，选取叶轮转速n，流量Q、扬程H、轴功率TP作为BP-ANN预测模型的输入变量，BP-ANN预测模型的输入层神经元数目为4，输出层神经元数目为1，即为贯流泵装置效率。隐含层神经元数量的确定采用下面计算式：

(6)

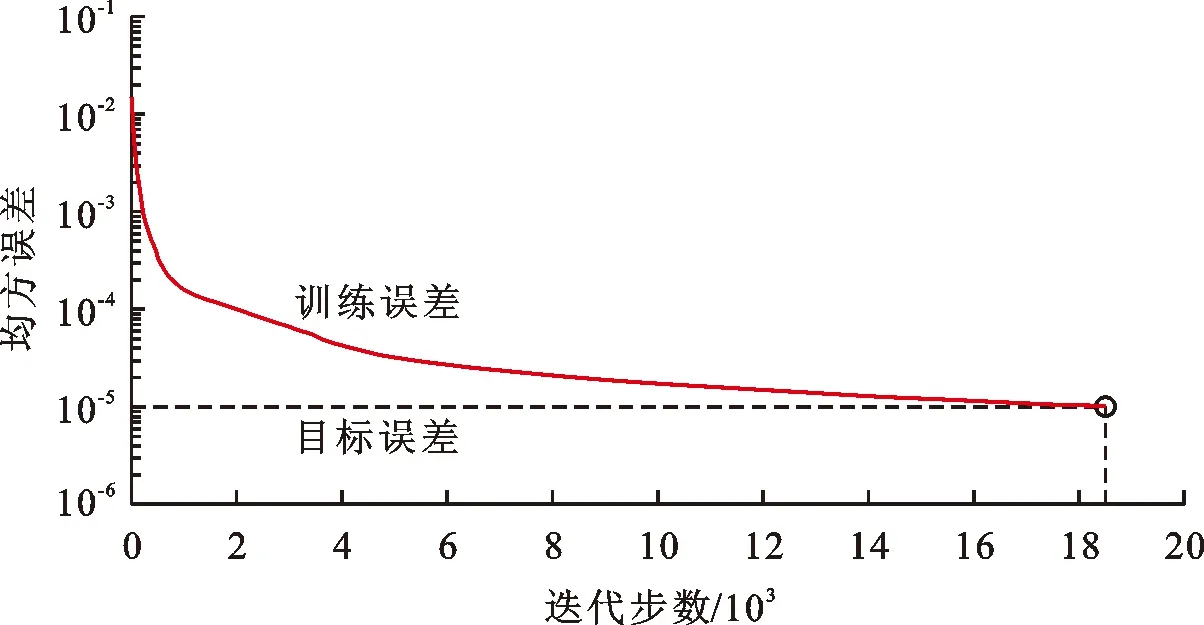
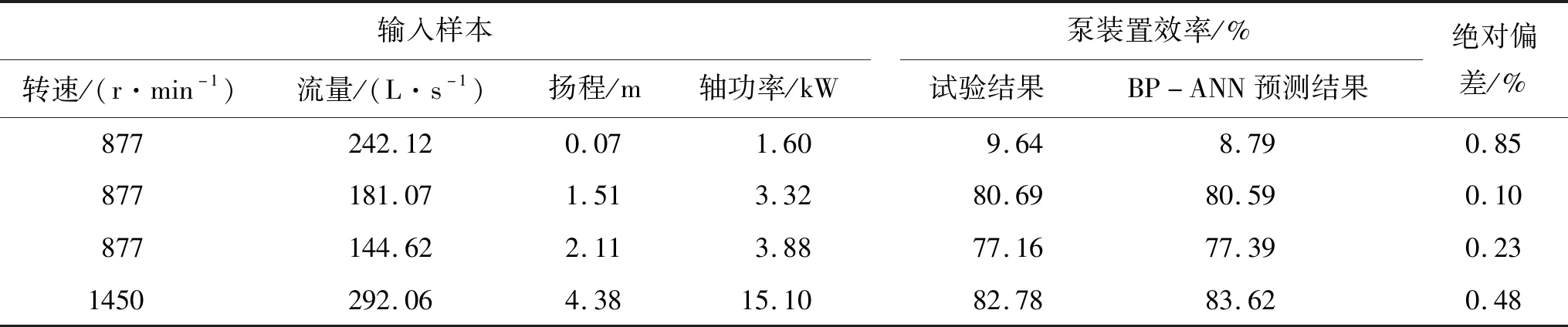
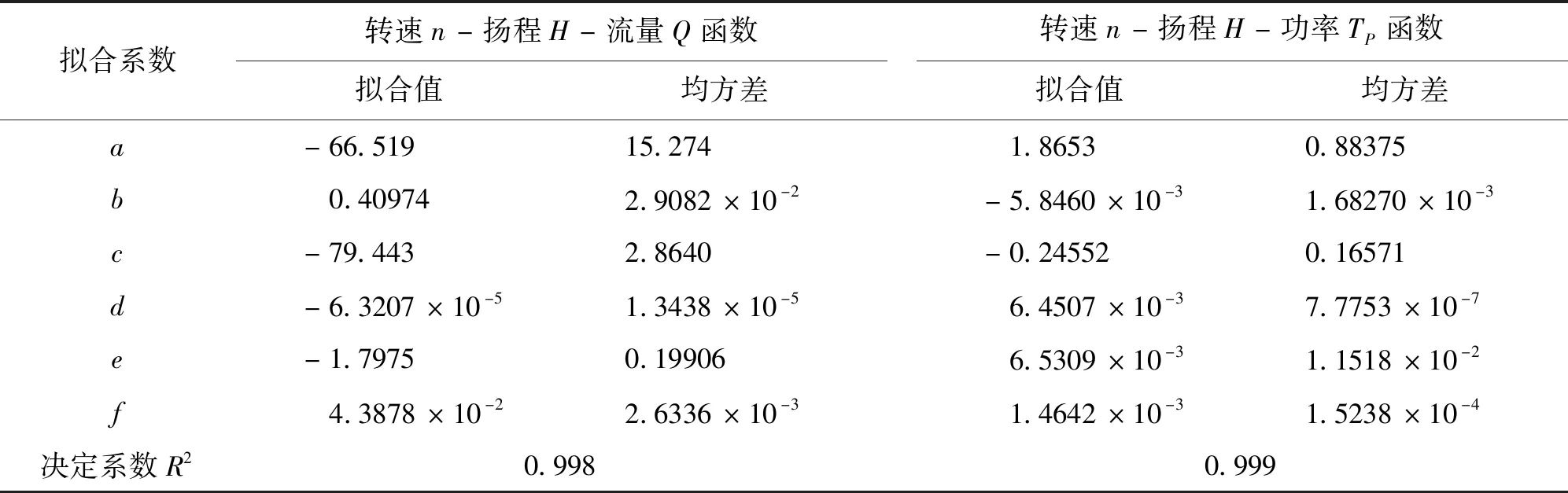
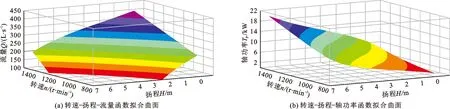
式中：Ay为隐含层节点数；Ai为输入层神经元数目，即样本指标数；Ao为神经元数目；a为常数且1

4.2 训练样本及模型构建

本次试验共有50组不同转速贯流泵装置的能量性能数据，为保证BP-ANN预测模型的学习精度，将43组数据用于训练样本，7组数据用于检验样本，训练样本的归一化处理、BP-ANN预测模型的构建及训练均参考文献[22]的方法。BP-ANN预测模型经18 491步的训练，BP-ANN网络预测精度达到10-5要求，均方误差曲线如图4所示。

5 BP-ANN预测模型的仿真和验证

以转速n=877 r/min时贯流泵装置的3组能量性能数据和转速n=1 450 r/min时贯流泵装置的1组能量性能数据共4组数据作为检验样本，BP-ANN预测模型的预测结果和物理模型试验结果如表2所示。

泵装置效率BP-ANN预测结果与试验结果的最大绝对偏差为0.85%，最小绝对偏差为0.10%，平均绝对偏差为0.415%，由检验样本的预测结果可知，BP-ANN预测模型的预测绝对偏差在1%以内，满足预测精度要求[22]。

在对不同转速的贯流泵装置能量性能参数预测时，需提供4个已知参数：转速、扬程、流量和轴功率，基于6种不同转速的贯流泵装置能量性能试验结果，通过曲面拟合法分别对转速n、扬程H和流量Q3个参量，以及转速n，扬程H和轴功率TP3个参量进行数值关系的曲面拟合，在确保曲面拟合精度的前提下，应采用简单的数学表达式，综合贯流泵装置的能量性能曲线特征，采用二次多项式曲面进行拟合，利用最小二乘法求解模型对曲面方程进行求解。

以(x，y，z)T(i=1，2，…，n)表示某空间曲面上的n个点坐标，二次多项式曲面方程可表示为：

z=a+bx+cy+dx2+ey2+fxy

(7)

式中：z为目标值；x和y分别为试验数据。

经求解计算可得两组参数二元函数曲面各项系数如表3所示。绘出扬程H、转速n与流量Q的数值函数关系和扬程H、转速n与轴功率TP的数值函数关系的二元函数曲面如图5所示。

图4 BP-ANN预测模型的均方误差曲线

表2 BP-ANN预测模型的预测结果和物理模型试验结果

表3 两组参数二元函数关系曲面的拟合系数

图5 贯流泵装置参数的二元非线性函数拟合曲面

根据贯流泵装置的叶轮转速和泵装置的扬程预测泵装置的流量及水泵的轴功率，然后基于BP-ANN预测模型对贯流泵装置的效率进行预测。

以水泵转速n=1 160 r/min，扬程H=2.87 m为例，采用上述方法预测该贯流泵装置的能量性能，并通过模型试验的数据给予验证。基于曲面拟合法获得泵装置流量Q=223.11 L/s，轴功率TP=7.99 kW，最后采用BP-ANN预测模型获得的泵装置效率为78.62%，经物理模型试验测试，该工况时泵装置的效率为79.07%，两者的绝对偏差值小于1%。

6 讨论

文献[23](2010年)通过CFD技术数值模拟了不同转速的混流泵装置的能量性能参数，并将数值模拟的泵装置能量性能参数与水泵相似律换算的结果进行对比，发现按水泵相似律对泵装置能量性能参数进行换算是存在误差的，但该文献未能给出变速运行泵装置能量性能换算方法。该文献通过数值模拟所得结论与本文通过理论分析和物理模型试验结果所得结论相一致，为解决不同转速泵装置性能换算的差异性，本文提出了基于BP-ANN的不同转速泵装置能量性能参数的预测方法，该方法首先构建了不同转速时n-H-Q的函数关系式和n-H-TP的曲面函数关系式，曲面函数关系式的构建方法与文献[24]基于曲面拟合法构建不同叶片安放角时水泵扬程和轴功率的预测方法相同，拟合曲面函数的决定系数均大于0.99，但文献[24]未对水泵效率的预测结果误差做出评价与分析，效率预测结果的准确性受扬程及轴功率预测值的综合影响，易导致效率预测误差的叠加。通过与文献[23]、[24]的研究方法和结论进行对比，本文解决了不同转速的泵装置能量性能参数换算的技术问题，尤其是泵装置效率的准确预测。