基于粗糙集-贝叶斯网络的流域水质评价方法

2022-10-26张万娟

水资源与水工程学报 2022年5期

白云，李勇，张万娟，贺嘉

(1.重庆工商大学管理科学与工程学院，重庆 400067；2.贵州医科大学环境污染与疾病监控教育部重点实验室，贵州贵阳 550025；3.西北农林科技大学经济管理学院，陕西杨凌 712100；4.重庆工商大学长江上游经济研究中心，重庆 400067)

1 研究背景

近年来，随着社会经济的飞速发展和城市规模的不断扩大，我国面临的水环境污染、水资源短缺和流域生态安全等问题日益突出，制约了区域经济社会的可持续发展，威胁着居民的饮用水安全[1-3]。在水环境的规划管理和污染治理中，对流域水环境质量进行科学的综合评价意义重大。目前，用于水质评价的方法主要有单因子指数法[4]、综合污染指数法[5]、多元统计分析法[6]、指数平滑法[7]、神经网络[8]以及灰色系统评价法[9]，以上方法在实际应用中各有利弊。单因子指数法将水质最差的类别作为评价结果，结果过于消极；综合污染指数法综合性强，但无法科学地确定各水质指标的权重；多元统计分析和指数平滑等统计方法结构简单，但不适用于非线性数据处理和多指标综合建模；神经网络和灰色系统等智能方法具有较强的自适应学习能力，但对数据要求严格[10]。流域水环境是一个动态系统，水质信息复杂多变且充满不确定性，作为当前概率推理和不确定性知识表达领域最有效的模型之一，贝叶斯网络能够更好地解决水环境不确定性问题，在水质预测评价等领域得到了更多的应用[11-13]。然而，由于水质监测数据本身所具备的不完整性、大量性、高维性和动态性等特点，单一的贝叶斯网络在水质评价方面还存在一定的不足。

粗糙集理论作为一种信息分析处理理论，其最大优点在于在没有先验知识的情况下也能够将不完整信息进行有效分析，从中发现隐含信息和潜在规律，从而获得最小知识表达[14]。近年来，粗糙集理论因其独特的数据分析能力而备受关注，在诊断、分类、预测、知识获取、数据挖掘等领域均有成功的应用[15-18]。目前，有学者已将粗糙集与贝叶斯网络结合起来开展研究，如Xiao等[19]将其应用于高速织机故障诊断，Xu等[20]将其应用于地震危险性定量评估，而将二者共同应用于流域水质分析的实例还未见报道。本文将粗糙集理论和贝叶斯网络联合应用于流域水质评价，在粗糙集属性约简的基础上，充分利用贝叶斯网络在不确定系统中的概率推理能力，合理评价嘉陵江流域重庆段的水环境质量，以期为流域水环境的科学管理及防控提供参考。

2 数据来源与研究方法

2.1 研究区概况

嘉陵江位于东经103°45′～109°00′、北纬29°20′～34°25′之间，全长1 345 km，流域总面积为16×104km2，是长江支流中流域面积最大，长度仅次于汉江的河流；其中，重庆境内长约153 km，是汇入长江的最后一个省级行政区，沿岸不仅有一些工业园和企业，还有许多城镇和居民点，工业废水、生活污水、农业面源污染物等多种水源均可进入嘉陵江，在一定程度上影响了流域水质。嘉陵江流域在重庆境内有3个水质监测断面，分别为北温泉、梁沱和大溪沟断面，均为重庆主城区重要饮用水水源地，且位于三峡库区上游，水质标准要求高，对其进行水质评价、了解其水质状况及水质变化情况尤为重要。嘉陵江流域重庆段水系分布及水质监测断面位置见图1。

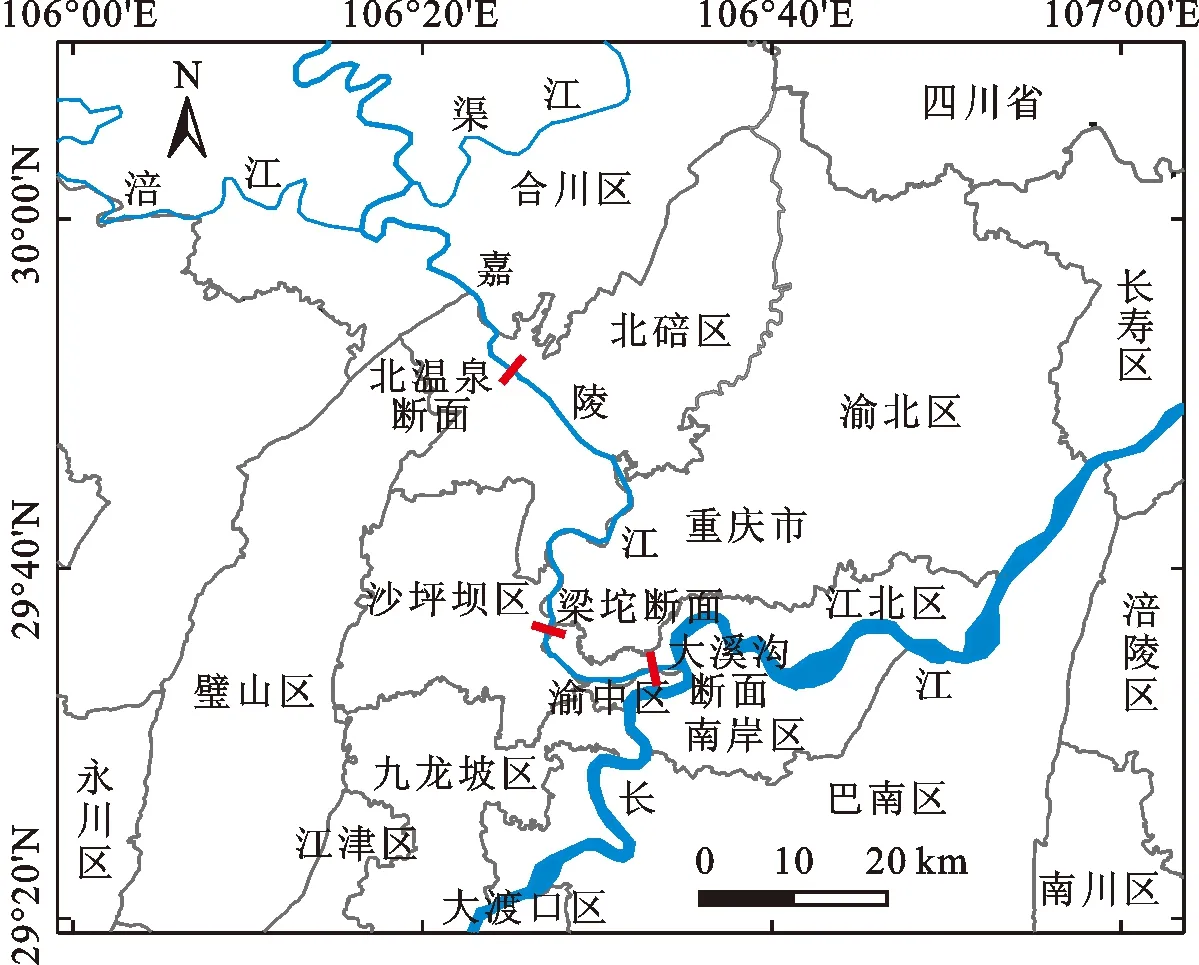
图1 嘉陵江流域重庆段水系分布及水质监测断面位置

2.2 数据来源

本文的研究范围为嘉陵江流域重庆段的3个监测断面，研究时段为2010-2016年。监测断面水质数据(内环境因素)来源于重庆市生态环境监测中心，其水质监测频率为每周1次，包括pH值、溶解氧(DO)、高锰酸盐指数(CODMn)、氨氮(NH3—N)和总磷(TP)等5个水质指标。根据《地表水环境质量标准》(GB 3838—2002)[21]将水质划分为五类。当5个水质指标数据均缺失时，则舍弃该周的数据，若部分缺失则使用均值/最大概率值法[22]对其进行填补，北温泉、梁沱和大溪沟最终分别有258周、349周和327周数据，数据缺失较为严重。选择季节(春、夏、秋、冬)、温度(平均温度、最高温度、最低温度)、降水量、天气(雨、阴、晴)作为可能影响水质状况的外环境因素，数据收集于全球天气网(http://lishi.tianqi.com/chongqing/)。

2.3 研究方法

2.3.1 粗糙集理论粗糙集理论(rough set,RS)是由Pawlak提出的可处理不精确和不完整信息的一种数据分析处理方法，其主要功能之一是对指标属性进行约简[23]。设有一个知识表达系统S=(U,A,V,f)。其中：U为论域，是由n个对象组成的非空有限集合；A为属性集，是条件属性集C和决策属性集D的并集；V为属性值的集合；f为信息函数，f：U×A→V，用以确定U中每个对象x的属性值。具有条件属性和决策属性的知识表达系统也叫决策表。

粗糙集通过定义1个参数即依赖度r来衡量D对C的依赖程度，公式如下[17]：

(1)

式中：card(·)为集合中的元素个数；POSC(D)为D关于C的下近似集，即能够全部被D包含的U中所有按等价关系C划分的集合；card(U)为论域U的元素个数。

在不同的内部和外部环境条件下，影响综合水质类别的因素也将有所不同，所以水质评价决策表，就是在保证流域水质各项指标正确归类的前提下，把水质评价决策表中不重要或不相关的影响因素剔除掉，进而形成1个最优属性集的简约结果。

2.3.2 贝叶斯网络贝叶斯网络(Bayesian network,BN)是由Pearl提出的一种基于图论和概率论的不确定知识表达模型，是智能化系统中处理不确定信息的主要方法之一[24]。对一个给定的水质指标时间序列，在贝叶斯网络建模前，首先计算水质节点的类别，公式如下：

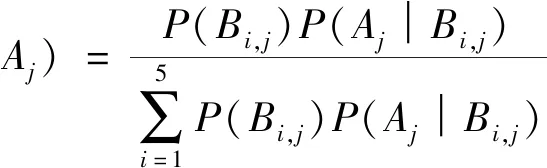
(2)

式中：i为水质类别，i=1,2,…,5；j为水质指标个数，j=1,2,…,5；Bi,j为某水质指标j为i类水质的标准值；Aj为某水质指标j的监测值；P(Bi,j)为先验概率，即根据先验知识判断水样为i类水的概率；P(Aj│Bi,j)为条件概率，即水质属于i类水时，监测值为Aj的概率；P(Bi,j│Aj)为后验概率，即监测值为Aj的条件下，水质类别为i的概率。

对于先验概率P(Bi,j)，在没有任何先验信息条件下，水样属于某一类别的概率相等，即P(B1，j)=P(B2,j)=P(B3,j)=P(B4,j)=P(B5,j)=1/5。

对于条件概率P(Aj│Bi,j)，计算方式采用距离法[10]，公式如下：

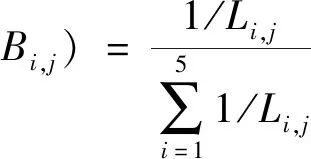
(3)

式中：Li,j=│Aj-Bi,j│，表示监测值Aj离标准值Bi,j的距离，Li,j越大，则水质属于i类水的可能性就越小。

通过公式(3)得出各水质指标对水质类别的后验概率后，即可计算多个指标下水质的综合后验概率Pi：

(4)

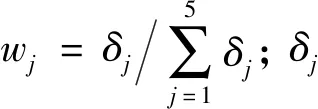
确定最终的综合水质类别，即将概率最大的水质类别作为最终所属类别c：

Pc=maxPi(i=1,2,…,5)

(5)

2.3.3 粗糙集-贝叶斯网络评价方法构建嘉陵江重庆断面水质评价的粗糙集-贝叶斯网络方法结构见图2，具体步骤如下：

步骤1：数据获取和预处理。收集内环境和外环境数据，对内环境数据缺失值采用直接删除或均值/最大概率值法[22]补齐的方式进行预处理。

步骤2：数据离散化。根据水质分类标准限值和Entropy/MDL算法[26]分别对连续型的内、外环境数据进行离散化处理。

步骤3：粗糙集属性约简。采用遗传算法[3]对流域水质的影响因子进行属性约简，得到每个属性的重要性。

步骤4：贝叶斯网络结构学习。采用K2算法[27]和文献分析结果构造流域水质评价模型的贝叶斯网络结构。

步骤5：贝叶斯网络参数学习。采用最大似然估计法[28]进行贝叶斯网络参数学习，得到网络中各指标节点的条件概率表。

步骤6：证据推理。采用联结树推理引擎[29]对节点的连接证据进行推理，获得综合水质类别。

步骤7：流域水质评价结果。

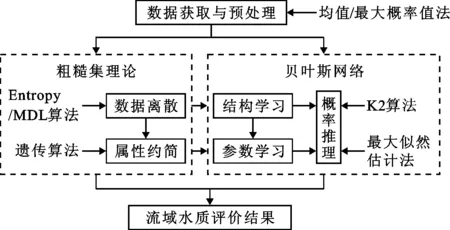
图2 粗糙集-贝叶斯网络水质评价方法结构

2.3.4 评估指标为了评估模型的水质预测效果，采用准确率(Ac)、精确率(Pr)、召回率(Re)和F1值作为模型评估指标[15]。公式如下：

(6)

(7)

(8)

(9)

式中：ZP为被正确分类为正例的数量；ZN为被正确分类为负例的数量；FP为被错误分类为正例的数量；FN为被错误分类为负例的数量。

3 结果与分析

3.1 流域水质指标分析

图3为嘉陵江流域重庆段3个监测断面水质指标的时间序列图。

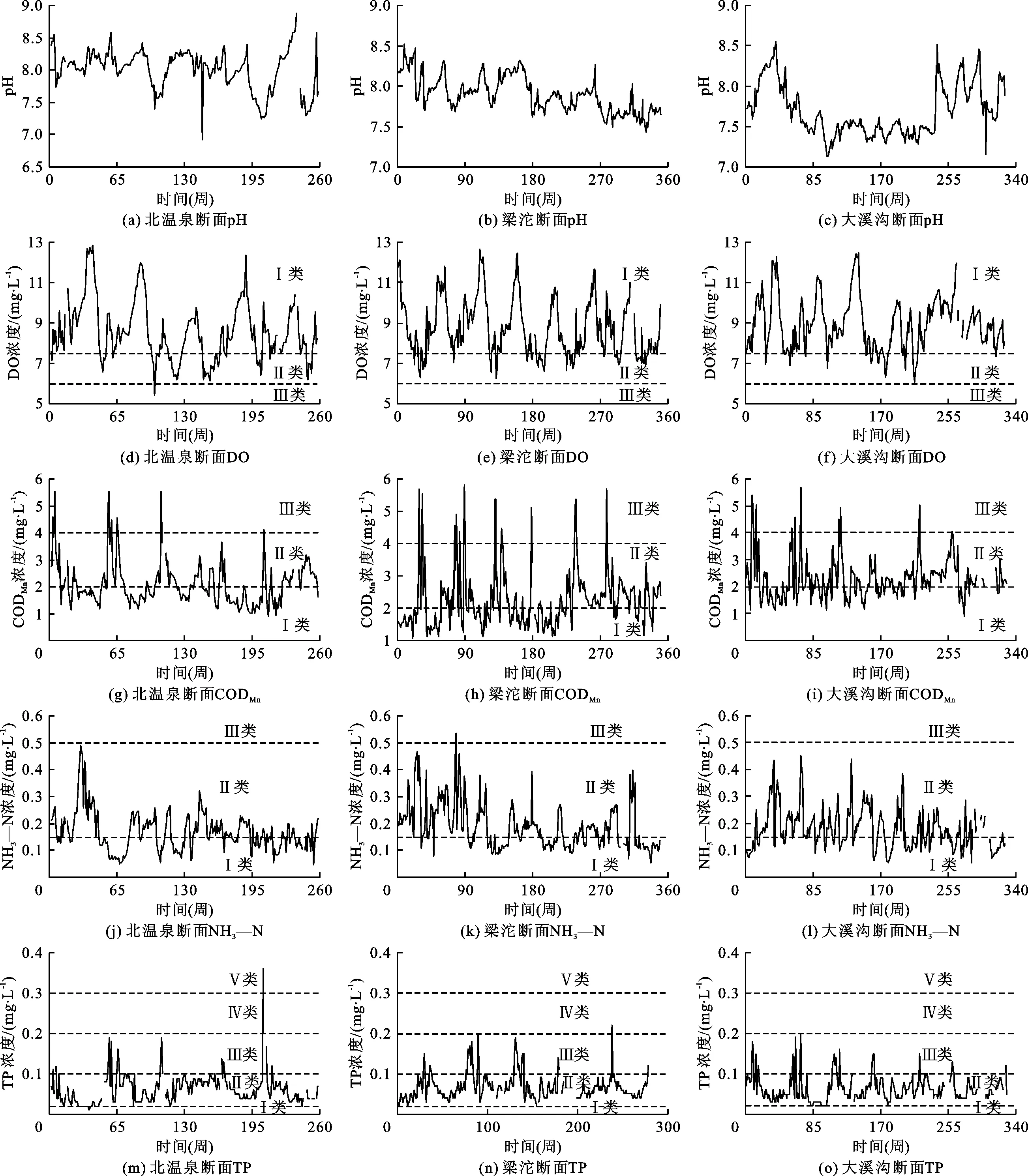
图3 嘉陵江流域重庆段3个监测断面水质指标的时间序列

由图3可以看出，除个别周的水环境质量为Ⅲ类以外，3个断面其他周的DO和NH3—N常年保持在Ⅰ类(DO浓度≥7.5 mg/L、NH3—N浓度≤0.15 mg/L)或Ⅱ类标准(7.5 mg/L >DO浓度≥6.0 mg/L、0.5 mg/L≥NH3—N浓度>0.15 mg/L)；相对而言，CODMn和TP污染较为严重，部分数据处于Ⅲ类水质标准(6 mg/L≥CODMn浓度>4 mg/L、0.2 mg/L≥TP浓度>0.1 mg/L)，北温泉断面有一突变点的TP甚至达到V类水质标准(0.4 mg/L≥TP浓度>0.3 mg/L)。此外，就时间序列的基本特征而言，数据缺失较为严重，波动性较大且无明显周期性，DO、COD、NH3—N和TP平均浓度分别为8.76、2.21、0.18、0.06 mg/L，标准偏差分别为1.38、0.81、0.08、0.03 mg/L，较高的标准偏差证实了此数据的不确定性，增加了水质模型评价的难度。

3.2 基于粗糙集的水质因子属性约简

3.2.1 数据离散粗糙集理论不能对连续型数据进行直接处理，在属性约简前，需对其进行离散化。对于DO、CODMn、NH3—N和TP等内环境因素，根据《地表水环境质量标准》中的水质分类标准进行离散化，Ⅰ～Ⅳ类水依次定义为状态1～5；对于pH值和连续型的外环境因素(平均温度、最高温度、最低温度、降水量)，采用Entropy/MDL算法进行离散化；对于字符型离散数据则直接定义离散值，天气因素将雨天、阴天、晴天分别定义为状态1、2、3，季节因素将春、夏、秋、冬分别定义为状态1、2、3、4。内、外环境因素的离散化结果分别见表1和2。

由表1可知，水质指标DO和pH值被分为两类，且状态1的数据较多，其余水质因子均是状态2较多；CODMn和NH3—N有3种状态，但状态3的数据较少；TP有5种状态，状态1、4和5的数据均较少。由表2可知，平均温度、最高温度、最低温度均有3种状态，数据分布较为均匀；降水量被分为6类，且状态1(无降水)的数据最多；天气则是状态1(雨天)>状态2(阴天)>状态3(晴天)。

3.2.2 粗糙集属性约简数据离散化后，采用遗传算法对水质的影响因素进行粗糙集属性约简。算法参数设计如下：总群大小和最大迭代次数分别为70和30，交叉概率和变异概率分别为0.7和0.05。由于需要综合考虑内、外环境因素对水质的影响，因此选择重要性大于0.4的属性作为约简集(若重要性大于0.6则有断面未涉及外环境因素)。3个断面的粗糙集约简结果见表3。基于表3的约简结果，则可进行贝叶斯网络的建模和分析。

3.3 基于粗糙集-贝叶斯网络的水质评价

3.3.1 贝叶斯网络结构学习选择数据集中的80%当作训练集进行网络建模，剩余的20%当作测试集进行网络验证。

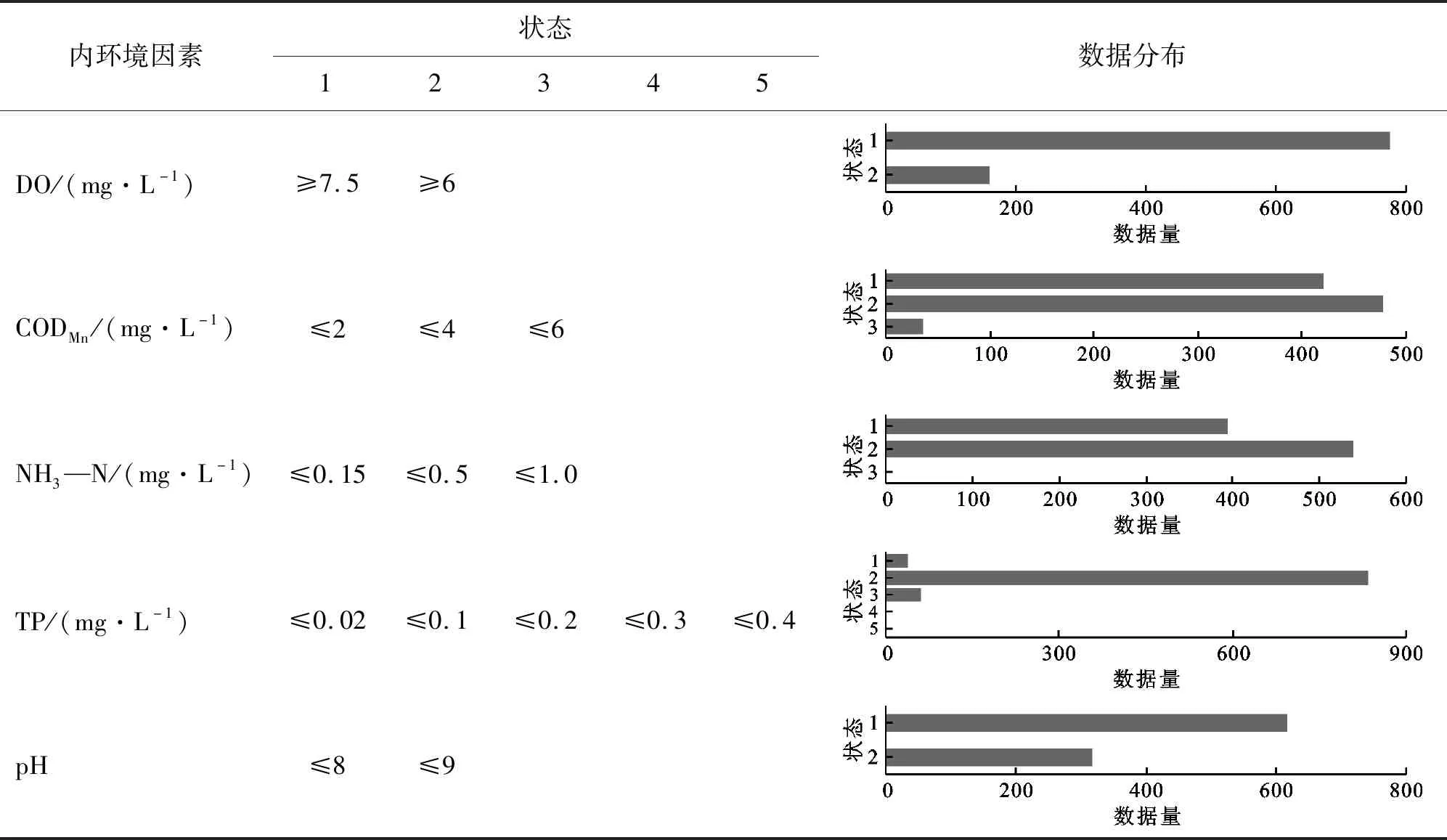
表1 内环境因素的离散化结果

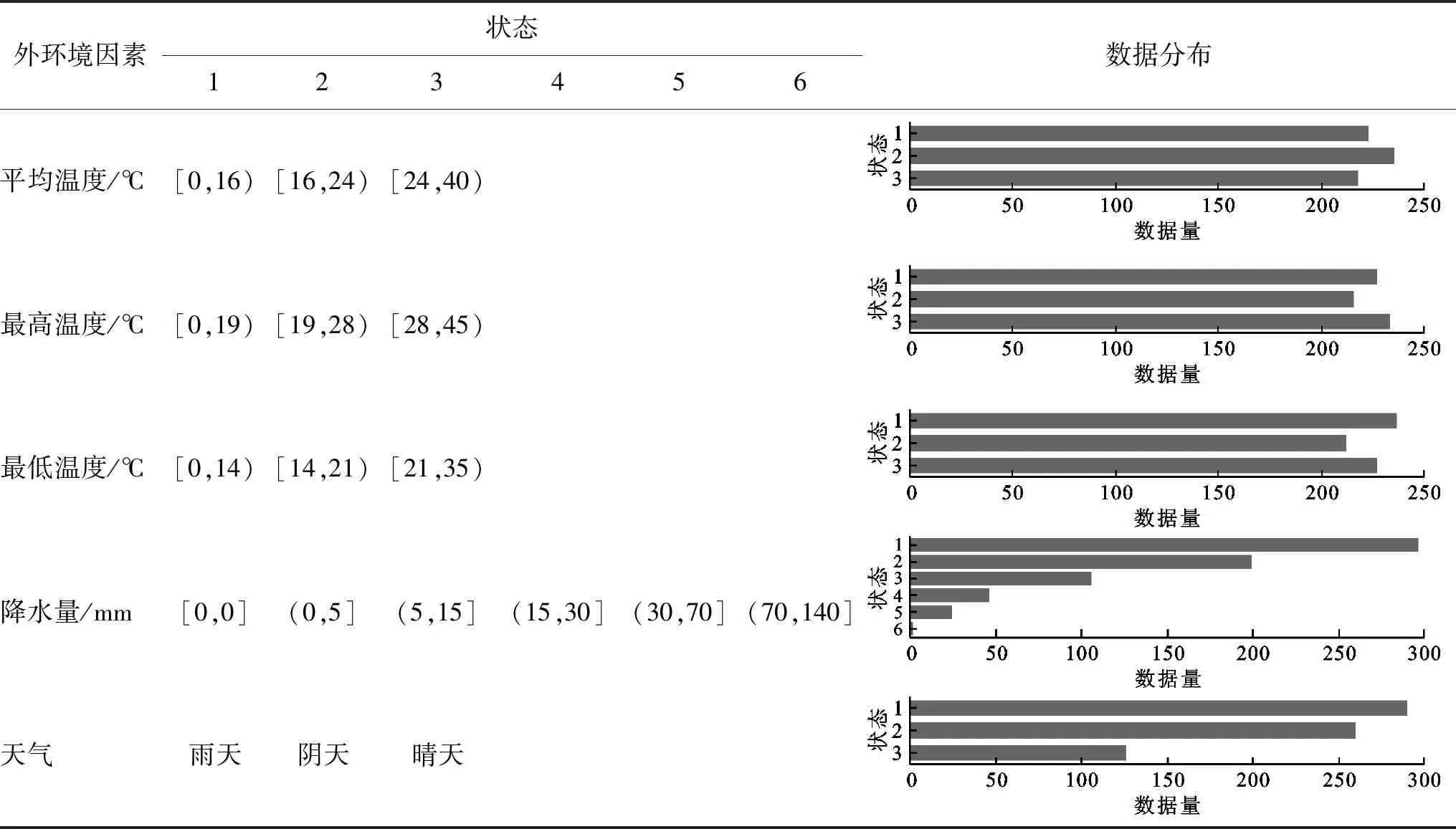
表2 外环境因素的离散化结果

表3 粗糙集属性约简结果

水质评价模型的贝叶斯网络结构通过K2算法和文献分析结果确定。首先，设置初始值，最大父节点数；节点状态数为离散节点的状态数；节点排序为节点的顺序，该模型设置的初始顺序为：外环境因素、内环境因素、水质类别。然后寻找每个节点在节点排序中的父节点，使用评分函数评价网络优劣，当新找到的父节点评分高于原结构时，将此节点作为当前节点的父节点，直到搜索完所有父节点，确定最终的网络结构。3个水质监测断面的贝叶斯网络结构见图4。

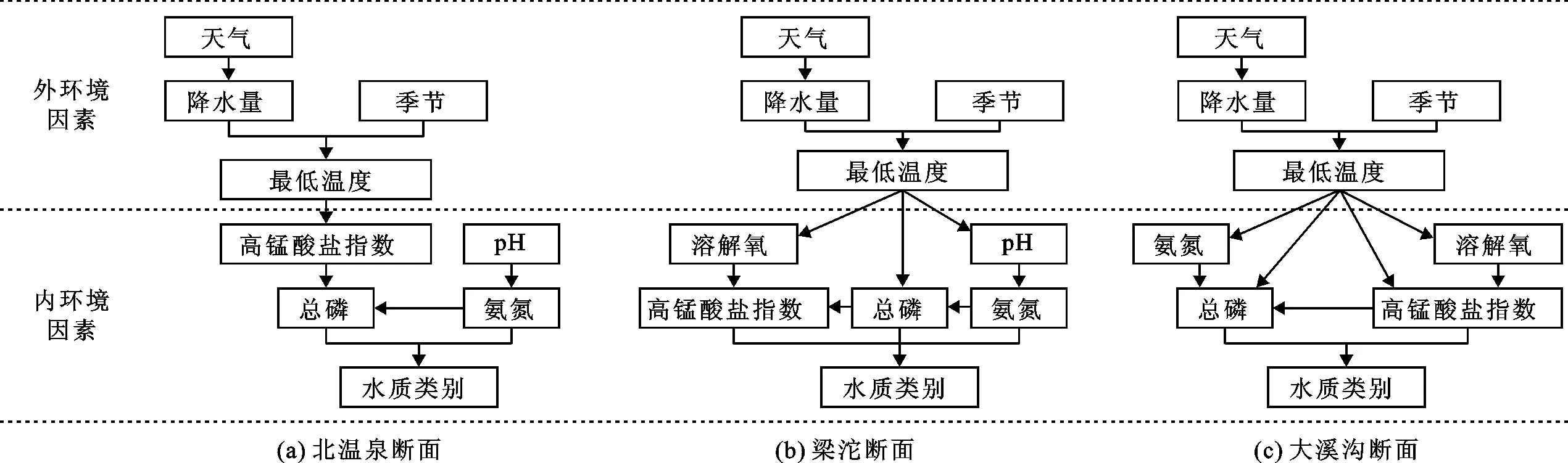
图4 3个水质监测断面的贝叶斯网络结构图

由图4可以看出，3个断面的网络结构均被分为两大部分，即外环境因素影响内环境因素，内环境因素影响最终水质类别。具体而言，3个断面的外环境影响因素相同，均涉及天气、降水量、季节和最低温度，且因果关系一致；3个断面的内环境因素存在差异，北温泉断面的DO、大溪沟断面的pH值与水质类别没有直接或间接联系，而梁沱断面的水质类别与5个内环境因素均存在关联性；对于北温泉断面，最低温度影响CODMn浓度，TP和NH3—N浓度直接影响水质类别的划分(图4(a))；梁沱断面的网络结构比北温泉断面复杂，最低温度可直接影响DO、TP和pH值，而直接影响水质类别的因素有CODMn、TP和NH3—N(图4(b))；对于大溪沟断面，NH3—N、TP、CODMn和DO均受最低温度的直接影响，水质类别则直接受TP和CODMn的影响(图4(c))。值得注意，TP与3个监测断面的综合水质类别均有直接关系，表明嘉陵江重庆段水质的主要污染指标是TP，造成TP污染严重的原因包括山地地形、生活污染、工业污染和农业污染等[1,30]。

3.3.2 贝叶斯网络参数学习贝叶斯网络结构建立后，使用最大似然估计法进行参数学习，得到网络节点的条件概率表，进而推算各个节点对目标节点的影响。首先分析外环境因素对水质状态的影响。分析发现，季节和最低温度对3个断面的水质影响较大，具体表现在夏季的水质最差，出现Ⅲ类及以上水质的概率明显大于其他季节(表4)；与夏季相对应，高温时水质状态最差，例如，随着最低温度的升高，Ⅲ类水质的概率逐渐增大，北温泉断面从2%增加到10%，梁沱断面从16%增加到37%，大溪沟断面从0增加到10%(表5)。相较而言，天气和降水量对水质状态的影响较小，本文通过梁沱断面的降水情况来举例分析，结果见表6。

表4 不同季节对3个断面水质状态的影响占比 %

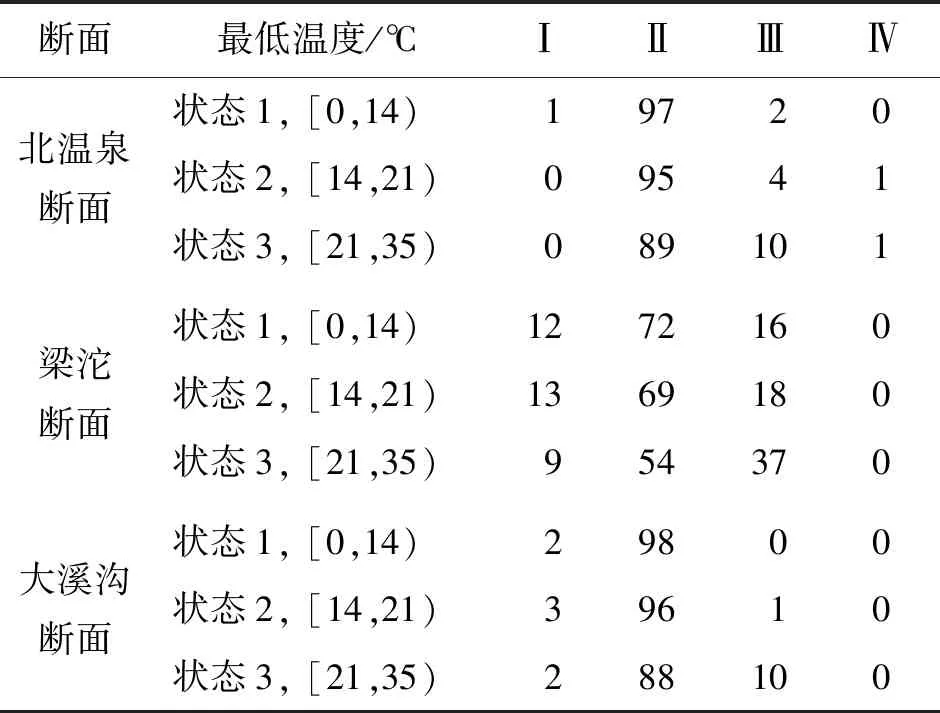
表5 不同温度对3个断面水质状态的影响占比 %

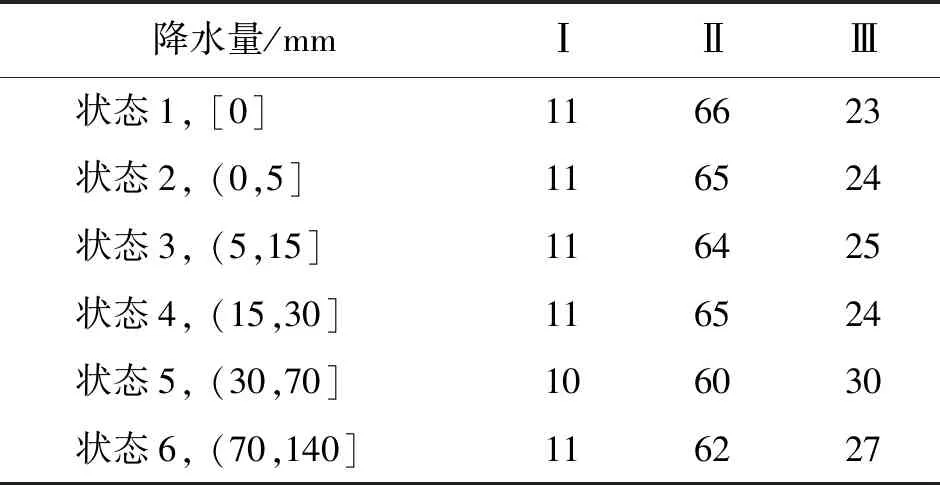
表6 梁沱断面不同降水量对水质状态的影响占比 %

由表6可知，当降水量≤30 mm(状态1～状态4)时，水质状态的概率变化很小，即降水量几乎不影响水质状态；当降水量>30 mm(状态4～状态6)，降水量对水质状态影响波动较大，出现Ⅲ类水质的概率先增大后减小。分析其原因，可能与雨水的冲刷作用和稀释作用有关，一方面，降水可将环境中的灰尘、污水、垃圾带入流域，导致水质状态变差；另一方面，强降水又能稀释流域中的污染物浓度，但Ⅲ类水质的概率还是偏高[31-32]。

其次，分析水质节点对最终水质状态的影响，3个断面水质节点的条件概率表见表7～9。表7～9中的结果是当水质节点是某种组合时对水质类别进行分类的概率。与贝叶斯网络结构图不同，条件概率表除了可以看到影响水质类别的指标，还能清楚看见节点间的概率传递，节点的组合决定了流域水质的状态，每一组概率组合都有不同的水质类别概率。以北温泉断面为例，概率表中有7种可能的组合(表7)，当TP和NH3—N的状态均为1时，水质各有50%的概率符合Ⅰ类和Ⅱ类标准；当TP和NH3—N有一个指标的状态变为2时，水质类别100%为Ⅱ类；当TP和NH3—N的状态均为2时，Ⅱ类水和Ⅲ类水的概率分别为98%和2%。

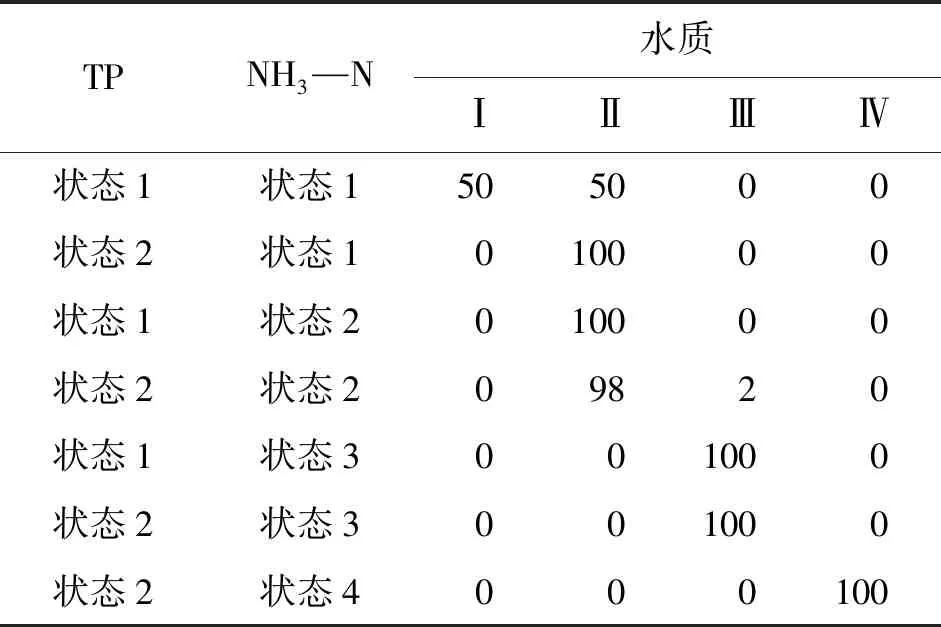
表7 北温泉断面水质节点的条件概率表 %

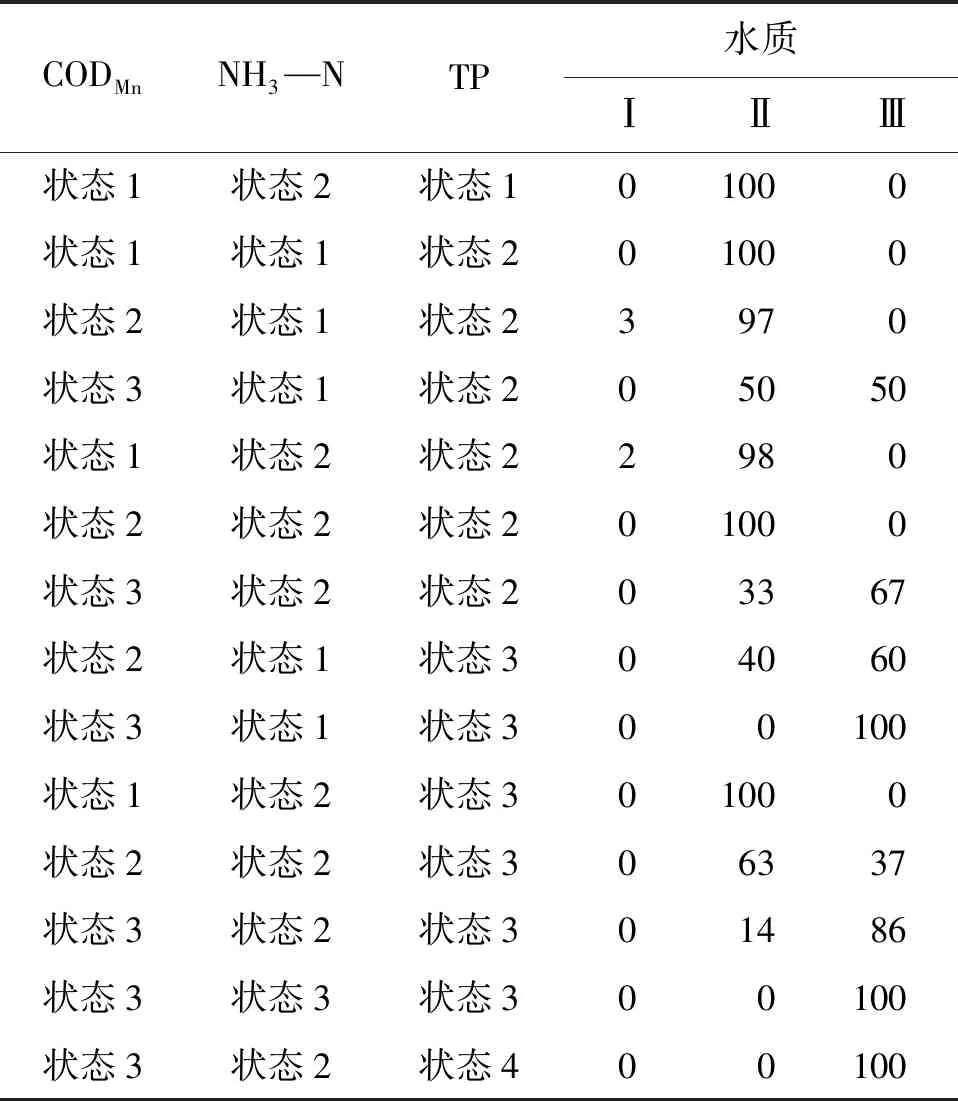
表8 梁沱断面水质节点的条件概率表 %

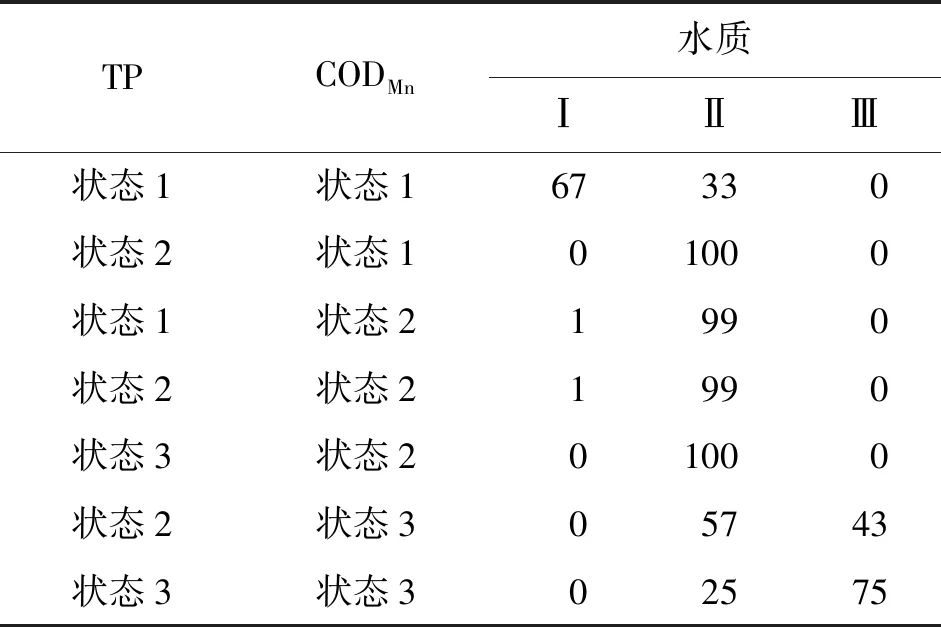
表9 大溪沟断面水质节点的条件概率表 %

3.3.3 水质评价结果获得贝叶斯网络中各节点的条件概率表后，利用联结树推理引擎进行证据推理，实现最终水质评价过程。嘉陵江流域重庆段各监测断面水质综合评价结果如表10所示。由表10可知，3个断面的水质评价类别均为Ⅱ类，但从隶属概率上可以发现，相对于北温泉和大溪沟断面，梁沱断面的水质状态较差，有24%的概率为Ⅲ类水质。

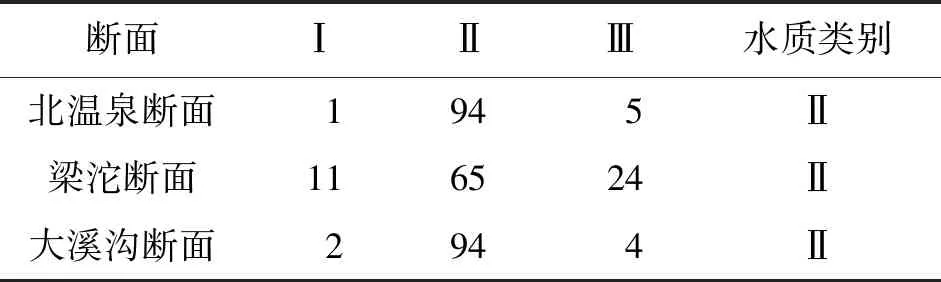
表10 嘉陵江流域重庆段各监测断面不同水质类别占比及评价结果 %

4 讨论

基于流域水质指标分析(图3)发现，与大多数流域水质序列相似，嘉陵江流域重庆段水质序列存在着数据缺失、冗余、动态、不完整和不确定的特点，且受多种外环境因素的共同影响，综合评价难度较大。粗糙集(RS)理论作为一种新的处理不完整知识的数学方法，能在保留关键信息的前提下对数据进行约简；然而，如果约简后的信息存在重要属性缺失时，RS理论将不能很好地开展属性约简和分类分析，决策效率相对较低。贝叶斯网络(BN)具有严格的概率论基础，其优秀的不确定性处理能力可以很好地解决上述问题，但是当属性较多时存在计算规模较大的问题。因此，基于智能互补的思想，应用RS理论降低BN模型的复杂度的同时，应用BN模型解决人工智能领域解释性差的问题，提出了粗糙集-贝叶斯网络(RS-BN)的流域水质评价方法，即使用RS理论发现水质时间序列规则并找到最小属性集，采用最小属性集进行BN建模得到网络结构和条件概率表，最终实现水质的证据推理并获得综合水质类别。

为了更好地验证本研究方法的可靠性，选用贝叶斯网络(BN)、灰色-贝叶斯网络(grey relation analysis-Bayesian network,GRA-BN)、粗糙集-朴素贝叶斯(rough set-naive Bayes,RS-NB)对相同数据集进行建模和比较分析。BN和GRA-BN模型采用与RS-BN相同的贝叶斯网络学习和贝叶斯网络推理方法，主要差别体现在模型输入，BN模型没有对输入属性进行约简，3个断面均采用所有内、外环境因素建模；GRA-BN模型采用灰色关联性进行属性约简，并选择关联程度大于0.95的属性进行建模。RS-NB模型采用粗糙集属性约简集进行建模，北温泉、梁沱、大溪沟3个断面的RS-NB模型参数分别为9、10、9。

4种水质评价方法的性能指标对比见表11。表11显示：(1)与BN模型相比，RS-BN方法的四个指标均有提升，说明粗糙集理论可以有效降低建模的冗余信息和不完整信息，提高模型效率和精度；(2)与GRA-BN方法相比，RS-BN方法拥有更好的预测效果，说明粗糙集理论拥有比灰色理论更好的信息属性约简能力；(3)与RS-NB方法相比，RS-BN方法具有更好的水质评价性能，凸显了BN模型在不确定问题处理和概率推理方面的能力。所以，本文提出的RS-BN方法获得了最高的准确率、精确率、召回率和F1值，水质评价效果最好。本研究很好地印证了前人提出的先约简、后预测的建模思路。如吴雨辰等[17]对9·6北海道地震滑坡易发性评价时发现，RS约简后神经网络模型的准确性将提高47.96%。此外，RS-BN方法应用于三个断面的模拟结果一致，均具有最高的模拟精度，相对而言，其他3种方法在不同断面表现出不同的模拟效果，说明RS-BN方法具有更好的普适性，能够在其他断面或流域的水质评价中推广使用。