Unusual thermodynamics of low-energy phonons in the Dirac semimetal Cd3As2

Zhen Wang(王振) Hengcan Zhao(赵恒灿) Meng Lyu(吕孟) Junsen Xiang(项俊森)Qingxin Dong(董庆新) Genfu Chen(陈根富) Shuai Zhang(张帅) and Peijie Sun(孙培杰)

1Beijing National Laboratory for Condensed Matter Physics,Institute of Physics,Chinese Academy of Sciences,Beijing 100190,China

2School of Physical Science,University of Chinese Academy of Sciences,Beijing 100049,China

3Songshan Lake Materials Laboratory,Dongguan 523808,China

Keywords: Dirac semimetal,low-energy phonon,thermal conductivity,lattice instability

1. Introduction

In addition to their electrical and optical properties that have been subjected to intensive investigation, topological semimetals also show intriguing lattice dynamics and thermal properties that remain largely unexplored. Most of these properties concern the interplay between topological electronic bands and low-energy phonons, as highlighted in the following cases: chiral magnetic effect can alter optical phonons via intrinsic plasmon modes in an external magnetic field;[1]topological singularity in electronic bands is able to induce chiral Kohn anomaly in the phonon dispersions;[2]topological phononic and electronic bands in a class of triplepoint metals are expected to offer a strategy for enhanced thermoelectricity,[3]etc.

The titled compound Cd3As2is a prototypical Dirac semimetal.[4]It has, on one hand, very high electron mobility derived from symmetry protected Dirac nodes and,on the other hand, surprisingly low lattice thermal conductivity that is indicative of strong phonon scatterings (Refs. [5–8]). The latter phenomenon becomes interesting because of the topological Dirac bands that appear to be highly relevant to lattice dynamics. Thus far, low thermal conductivity has been intensively investigated in thermoelectric materials, most of which host weak chemical bonds that are crucial for reducing phonon velocity and increasing scattering.[9]For Cd3As2,a group of soft optical phonons showing Kohn anomaly associated with the Dirac nodes have been identified byab initiocalculations.[10]These soft optical modes were ascribed to be the leading reason of the low thermal conductivity by increasing the scattering rate of heat-carrying acoustic phonons.In fact, significant softening of low-energy phonons is generically expected in semimetals near topological phase transition, where Kohn anomalies due to intranode or internode electron–phonon scattering may occur near the Brillouinzone center.[11]Accordingly,Raman scattering of Cd3As2has shown significant deviations of selected optical-phonon frequencies from the expectation based on lattice anharmonicity belowT ≈100 K (Ref. [12]). This has been ascribed to the strong fluctuations of lattice degrees of freedom interacting with Dirac electrons.

From a crystallographic point of view,Cd3As2at ambient conditions crystalizing in the tetragonally distorted antifluorite structure (space groupI41/acd) that hosts topological Dirac bands is located close to a lattice instability. Upon heating to only about 220°C, it transforms to a Zn3As2-type structure with space group(P42/nbc),with at least two more structural phase transitions taking place at higher temperatures,[13,14]Alternatively, application of pressure causes a couple of structural phase transitions as well,starting from the one at a relatively low pressure of～2.3 GPa.[14–16]Given the complex lattice instability as introduced above, an in-depth investigation on this compound by a comprehensive set of thermodynamic probes appears to be essential in characterizing the lattice dynamics and, more importantly, its potential interaction with Dirac electrons.

2. Experimental methods

Single crystals of Cd3As2were prepared by self-transport technique;see Ref.[5]for the details of structural characterization and crystal orientation. The specific heat was measured by thermal relaxation method in a commercial physical properties measurement system (PPMS, Quantum Design), and the thermal conductivity by conventional steady-state method with two thermometers and one heater.[5]The measurements of thermal expansion were performed by using a miniaturized capacitance dilatometer and an Andeen-Hagerling 2500A capacitance bridge.[17]We have also measured the transverse and longitudinal ultrasound velocitiesυTandυLof a large polycrystalline sample(2.67×1.97×0.96 mm3). Here,the sound velocities were measured by a phase comparison technique,[18]where the frequency of the input acoustic wave was continuously adjusted during the temperature scan in order to maintain a constant phase of a given output echo. The elastic moduli were calculated from the ultrasound velocities asCi=dυ2i(i=L or T),withdbeing the sample density.

3. Results and discussion

The thermal conductivityκ(T) measured within the asgrown(112)plane of a single crystal is shown in Fig.1. Thermal measurements in the(100)plane have revealed very similar data,[8]indicating weak anisotropy of the thermal conductivity in Cd3As2. The electronic contributionκe(T)calculated based on the Wiedemann–Franz law and the measured electrical resistivity (Fig. 1 inset) are also shown. In estimating the electronic part, we assume that the Sommerfeld value of the Lorenz number applies to this material in the temperature window of interest. We note, however, that to what extent the Wiedemann–Franz law holds in Dirac materials remains an issue of debate. For example,the Sommerfeld value of the Lorenz number may change significantly when a magnetic field is applied[19]or the Fermi level crosses the Dirac point;[20]the two situations that do not apply to the current work and Cd3As2. In spite of a moderate sample dependence of theκ(T)profiles reported in the literature,[7,8,21]they are qualitatively similar with two marked features: a nearly temperature-independent, small value ofκ(T) atT ＞100 K and a markedκ(T)maximum atT≈10 K.The lattice thermal conductivity (κL≈κ-κe) atT ＞100 K falls into the range of the uncertainties(±0.6 W/mK at room temperature)in our measurements,whereas the averageκLreported in Ref.[8]is only 0.7 W/mK in the wide temperature range of 100-300 K.The small value ofκL(T) and its weak temperature dependence atT ＞100 K indicate that the phonon mean free path is probably reduced to about its lower limit in this temperature

Fig. 1. The thermal conductivity κ(T) measured within the as-grown(112)plane of Cd3As2. Error bars denote standard deviations estimated from the average of measurements under multiple temperature gradients. The electronic contribution κe(T) (red solid line) is estimated fromtheWiedemann–Franzlaw,κeρ/T=L0,withthe Sommerfeld valueoftheLorenznumberL0≡=2.44×10-8 W·Ω·K-2.

Considering a reasonable value ofκL≈0.7 W/mK forT ＞100 K(Ref.[8]),the phonon mean free pathlis estimated to be 6.96 ˚A,which is even shorter than the lattice parameters of Cd3As2,i.e.,a=b=12.67 ˚A andc=25.35 ˚A.Note that,this is only a naive and rough estimate because on one hand the kinetic description of thermal conductivity is likely on the brink of failure for Cd3As2with a large primitive cell,[22]and on the other hand the real phonon mean free path is actually mode dependent. Nevertheless, such estimate is meaningful because it confirms that the lattice thermal conductivity is already at or not far from its lower limit. The pronounced increase ofκ(T)below 50 K is a typical feature originated from phonon–phonon Umklapp processes,and the drastic decrease below about 10 K can be attributed to boundary scatterings of heat-carrying phonons in semimetals and semiconductors.[23]Here, the temperature-dependent specific heat determines the temperature profile ofκ(T) because the phonon mean free path is a constant. Though how the Dirac electrons impact onκLcannot be straightforwardly observed, it can be reliably inferred fromκLas a function of the field: whileκLis vanishingly small in zero and small fields (B ＜2 T) where Dirac electrons are highly mobile, it increases gradually and becomes dominant in higher fields where Dirac electrons are spatially constrained by the magnetic fields; seeκ(B) shown in Fig.2(e)of Ref.[5].

Before proceeding with other experimental results, we stress that a simple inspection into the crystal structure of Cd3As2can already yield important insight into the unusually lowκLvalues. Cd3As2crystallizes in a large primitive cell with the number of formula unitZ= 16, i.e., totallyN=80 atoms in one primitive cell. A large primitive cell means that the reciprocal space is predominantly occupied by a large number(3N-3)of optical modes. As a result,the thermodynamically-weighted heat capacity and the Debye temperature for heat-carrying acoustic phonons are greatly suppressed. This causes a reducedκLfrom purely crystallographic reasons, as can be inferred from the aforementioned kinetic description for thermal conductivity. Such a strong reduction trend ofκLwith increasing primitive cell volume has been already reported previously.[24]

Fig. 2. (a) The low-temperature specific heat of Cd3As2 depicted as C/T3 vs T. The data is fitted by considering a Debye term and two Einstein modes (blue solid line). Dotted and dashed lines are individual contributions from the Debye term and the leading Einstein mode,respectively(see text). (b)The low-temperature C(T)deviates strongly from Debye’s T-cube law that is commonly described by a linear dependence of C/T versus T2. By contrast, the description based on the combined Debye and Einstein terms(blue solid line)can reasonably reproduce the curved C/T(T2)line. Inset: T-dependent specific heat of Cd3As2.

With the unusual thermal conductivity in mind,below we examine the specific heat carefully. Figure 2(a) displays the low-temperature specific heat asC/T3versusT. While the specific heat within Debye’s description will obey aT-cube law and appear constant in this representation, an enhanced and broad peak is observed for Cd3As2atT ≈10 K. This is a thermodynamic signature of dominant low-energy optical modes, and has been intensively studied for cage compounds with“rattling”guest ion.[25]According to a rule of thumb obtained previously, the Einstein temperatureθEcharacterizing these modes is five times the temperature position of theC/T3vs.Tmaximum,which meansθE≈50 K in this case.

The specific heat shown asC/TversusT2forT ＜8 K in Fig. 2(b) further demonstrates the importance of low-energy Einstein modes. Different to the expectation from Debye’s description,theC/T(T2)variation deviates significantly from a straight line. A linear dependence ofC/T(T2),if any,appears only atT2＜5,namely,below about 2 K,where the contribution of low-energy optical models freezes out.Considering the significant contribution from soft optical phonons in the temperature window of interest,we combine Debye’s description and a couple of local Einstein modes to fitC(T),

HereRis the gas constant,andAnis the number of Einstein oscillations andN0is the number of atoms per formula unit. The result of fitting is shown by the blue solid line in Figs.2(a)and 2(b), from which we obtainθD=111 K andθE1=42 K. A second Einstein mode withθE2=101 K,which is less important compared to the first one, was also included for a better fitting. Markedly, the fit can capture the prominent features in specific heat including the broad peak inC/T3versusT(Fig.2(a))and the curvedC/TversusT2at low temperatures(Fig.2(b)).

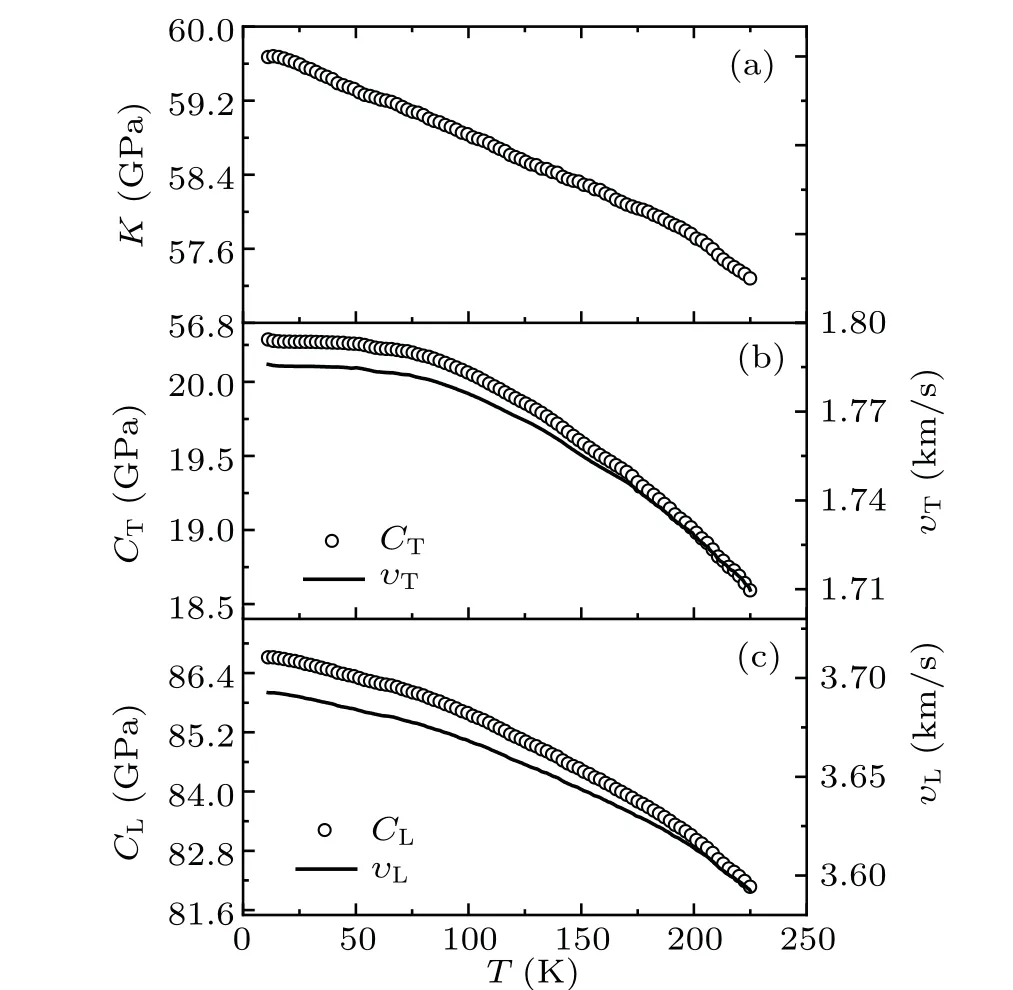
Fig. 3. Longitudinal (CL) and transverse (CT) elastic moduli and the calculated bulk modulus K =CL-CT as a function of temperature for Cd3As2. The corresponding longitudinal (υL) and transverse (υT)sound velocities are also shown(right axis).

From the longitudinal and transverse sound velocities of Cd3As2,the average sound velocity ¯υcan be calculated as follows:

From Eq.(2),one readily obtains ¯υ=1943 m/s for 200 K and 2005 m/s for 10 K. The moderately small sound velocities,which measure the phonon dispersions at the Brillouin zone center,are not the leading reason of the extremely low thermal conductivity. For comparison, FeSb2, which has an average sound velocity of 3110 m/s (less than double ¯υof Cd3As2)reveals a lattice thermal conductivity of several tens of W/mK at 100 K(Ref.[26]). Furthermore,the Debye temperatureθDcan also be estimated from the average phonon velocity

HereVis the primitive cell volume andhthe Planck’s constant. The estimated Debye temperature,θD=187 K,is considerably larger than that evaluated from the specific heat,θD=111 K.Unlike the specific heat which measures the thermodynamics of all low-energy phonons via the phonon density of states,sound velocities probe the group velocities of acoustic phonons at the low frequency limit and are less influenced by low-energy optical modes. The strong disagreement between the two values ofθDhints at a strong deviation of the low-energy phonons from Debye’s description,again pointing to the importance of low-energy optical modes in the description of the thermodynamic properties.

Figure 4 shows the linear thermal expansion coefficient estimated from the measured length change dL,α=1/L(dL/dT), as a function of temperature. Here,αis measured alongcaxis of single-crystalline Cd3As2, which is the direction where Dirac cones are located.[10]In general,α(T)behaves similar toC(T)(Fig.2 inset);it reveals,however,negative values below about 10 K.Given the experimental resultsK(T),C(T)andα(T),one can easily estimate the Gr¨uneisen ratioγ=3VmKα/Cas an experimental indicator of lattice anharmonicity,whereVmis the molar volume.

Fig. 4. Thermal expansion coefficient α measured along c axis (left)and the estimated thermodynamic Gr¨uneisen ratio γ (right). Drastic drop of γ is observed at T ＜100 K,ending up with negative values at T ＜10 K.

As shown in Fig.4(right axis),γ(T)remains 1.1(±0.1)in a wide temperature range above 100 K.This is a Gr¨uneisen ratio within the range of common expectation for simple solids.AtT ＜100 K,γ(T)reveals a drastic drop and becomes negative atT ＜10 K, corresponding to the low-temperature negative thermal expansion. The temperature window whereγ(T) drops significantly matches well to that where Einstein modes are observed in specific heat(Fig.2). Phenomenologically, the unusual behavior ofγ(T) originates from the temperature dependence ofα(T)that shows stronger decrease below 100 K relative to that ofC(T)towards negative values at low temperatures. Likewise, atT～100 K, strong frequency reduction of several optical phonons has been observed by Raman scattering,[12]and this temperature has been regarded as a characteristic energy scale of interband scattering in the Dirac states coupling to low-energy optical phonons. In line with the negative values ofγ(T) that indicate lattice instability at low temperatures, the tetragonal metallic phase of Cd3As2is indeed rather unstable and changes to a semiconducting monoclinic phase at a critical pressurepc≈2.3 GPa,[14,16]as has been mentioned above. Different from the general expectation that pressure drives an insulator or a semiconductor to a metallic phase due to band broadening,the opposite trend observed in Cd3As2indicates that the Dirac bands might play an important role in the structural instability,as inferred from our thermal expansion measurements. Because apparent anomaly is not observed in the elastic moduli,we speculate the unusualγ(T)behavior at low temperatures to be related to thermodynamics of low-energy optical modes.

4. Summary

To summarize, we have studied the low-energy phonons of Cd3As2by a comprehensive set of thermodynamic probes.As far as the extremely low lattice thermal conductivity is concerned, Cd3As2appears to be unusual in the following aspects: 1) A large unit cell sets a strong constraint on the thermodynamics of low-energy phonons, leading to reduced specific heat and enhanced phonon scattering rate of acoustic phonons; 2) Soft optical phonons, which are partially related to the Kohn anomaly caused by Dirac bands, can be clearly captured by low-temperature specific heat revealing significant Einstein terms; 3) A drastic decrease of the thermodynamic Gr¨uneisen ratio is observed below 100 K, where enhanced coupling between lattice and electronic degrees of freedom has been previously confirmed. The decrease ends up with a negative thermal expansion at low temperatures that is indicative of lattice instability. At last, we note that while it is safe to conclude that the Dirac electrons are relevant to the phonon softening and the lattice instability in Cd3As2,to what extent the interplay between lattice dynamics and Dirac electrons plays its role therein remains an interesting issue. Because very low thermal conductivities have been observed in a number of topological semimetals such as ZrTe5(Ref.[27]),further investigation and comparison between different compounds along this line appear to be an interesting project.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11974389, 12141002 and 52088101), the National Key R&D Program of China (Grant No. 2017YFA0303100), the Chinese Academy of Sciences through the Scientific Instrument Developing Project (Grant No.ZDKYYQ20210003),and the Strategic Priority Research Program(Grant No.XDB33000000).