一种改进的道路行车密度峰值模糊聚类算法

张正文， 邓 薇， 廖桂生， 巩朋成， 王兆彬

(1．湖北工业大学电气与电子工程学院， 湖北武汉 430068；2．西安电子科技大学雷达信号处理国家重点实验室， 陕西西安 710071；3．武汉工程大学计算机科学与工程学院， 湖北武汉 430205)

0 引言

在智能交通系统(ITS)中，多目标交通雷达作为道路交通辅助工具，可以监测雷达探测区域内全部车辆的运动状态信息，及时掌握道路车辆信息，有利于交管部门管控道路，减少交通事故的发生，提高道路的安全指数。基于毫米波雷达的交通流量计是典型的用来监测道路状况的装置，可以安装在路侧、路口红绿灯处、天桥等视野较好的高处。雷达通过接收发射出去电磁波的回波信号，获取道路车辆的运动信息，主要包括探测车辆的位置和速度等信息，实现对道路车辆运动轨迹的监测。多目标聚类是雷达回波数据处理中关键的一步，快速得到准确的聚类结果可以减小聚类误差在后续处理中产生的影响，减少后续跟踪等高级算法的计算量，提高相关算法的精度。近年来，多种经典聚类算法被应用在交通领域中，包括基于密度的DBSCAN聚类算法，基于分区的-means算法和模糊C均值(FCM)算法。基于密度峰值的聚类算法。文献[4]中的DBSCAN是基于空间数据点分布密度的算法，但当不同类数据相距较近时聚类效果会略差；基于分区的-means算法通过确定分类数目后，将距离作为分类指标，按照簇内的点分布紧密且簇间的距离相对大的规则进行聚类，直至聚类结果不再更新，此方法对值较敏感，以及随机确定的初始中心，会影响算法的收敛速度和聚类结果；FCM算法是模糊聚类算法，用隶属度表示每个数据点属于某簇的程度，通过求解目标函数最优值确定聚类中心和隶属度值。该算法具有较高的精度，但需要设置初始参数，如果参数初始化不合适，可能会影响最终聚类结果的正确性。其次，当数据样本集较大时，算法实时性不佳。结合城市道路场景，当道路上车流量较大、车辆相距很近时，雷达采样点分布会更加密集，此时运用传统FCM算法不能准确地识别相邻车辆。意大利Rodriguez等提出了一种基于密度峰值的快速聚类算法(DPC算法)，该算法主要思想是：1) 聚类中心的密度大于邻域密度；2) 聚类中心与其他高密度点的距离相对较大。DPC算法利用局部密度和相对距离划分样本点，处理过程简单又高效。但DPC算法根据决策图选取初始簇中心，若选取不当，将导致后续样本点聚类错误。

针对以上传统算法中的问题，结合毫米波雷达交通流量计中数据的特点，本文提出一种改进的基于密度峰值的FCM聚类算法：1) 对文献[10]中DPC算法的决策图做出改进，用改进后的决策图确定初始聚类中心。在决策图中使用自适应椭圆距离代替欧式距离，并在图中加入一条自适应函数曲线用以自动确定初始聚类中心；2) 根据步骤1)确定的初始聚类中心计算隶属度矩阵，将聚类中心坐标和隶属度矩阵作为FCM算法的初始条件，使用FCM算法更新聚类中心和隶属度，完成一次模糊聚类；3) 根据一次聚类结果计算各簇样本点的速度中位数，将速度中位数与一次模糊聚类更新的隶属度作为FCM算法初始条件，进行二次模糊聚类，得到最终模糊聚类结果。实验证明，提出的算法最终得到更为精确的聚类结果。

1 基于密度峰值的聚类算法

基于密度峰值的聚类算法核心是认定簇中心满足以下特征：1)簇中心的密度比其周围点的密度大，即簇中心为密度峰值点；2)簇中心之间的距离比簇中心到其他点的距离更大。根据这两个条件即可确定簇中心和簇数目。

(1)

式中为预设的截断距离，表示任意两点间的距离，当满足<0时，()=1，否则()=0。式(1)的物理意义为统计以点为中心，为半径的圆内样本点的个数，个数即代表密度大小。除了利用公式(1)中截断核计算局部密度外，还可以用高斯核计算局部点密度，其定义如下：

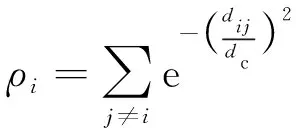
(2)

由公式(2)可知，高斯核表示的点密度为连续值，不会出现截断核密度中不同数据点具有相同密度值的现象，更有利于后续的数据处理。DPC算法中，在得到任意点的局部密度后，求各点的最小距离。最小距离由任意点与其他高密度点间的最小距离确定：

(3)

计算得到任意样本点的局部密度和最小距离后，以每个点的为横坐标，为纵坐标画如图1(a)所示的二维决策图，用户在决策图中，根据分布情况手动选择聚类中心点，通常将同时具有较大和较大的点定义为聚类中心，其余点分配到比自身密度高且距离最近的聚类中心所属的簇中。

图1(a)中横坐标为样本点密度，纵坐标为最小距离，红色标记点为选定的初始聚类中心，蓝色点为其他样本点。图1(b)是所有样本点分类后的二维坐标图，不同颜色的点为不同簇，黑色圆点是由二维策略图确定的聚类中心。

DPC算法需要在策略图中手动确定聚类中心，导致算法的运行效率低，在确定聚类中心后，仅根据各样本点到聚类中心的距离进行最终聚类，导致聚类结果准确率低。因此，本文提出的算法对DPC算法中的决策图进行改造，使用自适应椭圆距离代替欧式距离计算，进一步计算得到更可靠的和，并在决策图中引入自适应函数曲线自动判定聚类中心，提高聚类中心确定的效率。

图1 密度峰值聚类算法过程图

2 提出的算法

针对传统DPC算法中聚类中心的确定需要人工操作、聚类仅靠距离这一判定条件，本文对DPC算法进行改造，并使用FCM算法进行模糊聚类。首先，改进DPC算法决策图，使用自适应椭圆距离代替欧氏距离，计算样本点的局部密度和最小距离并将二者作为横、纵坐标，画决策图，在决策图中添加一条自适应函数曲线，以自动确定初始聚类中心；接着，将初始聚类中心信息代入FCM算法，根据距离信息构造目标函数，做一次模糊聚类；最后，在一次模糊聚类结果基础上，根据每簇的速度信息构造目标函数，做二次模糊聚类，以修正一次聚类结果。

2.1 初始聚类中心的确定

(4)

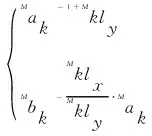
此计算方法设置，两个变量参数来调整数据之间的距离相关性，用来作为自适应椭圆距离的长轴、短轴参数，其分别为

(5)

(6)

其中，和分别由两点的横、纵坐标差决定：

(7)

此式通过自然数e将横、纵坐标差值转化为值域为[0,1]的变量，当横、纵坐标差变化时，和成反比例变化，接着公式(6)可自适应地调整和大小，从而确定长轴、短轴参数。假设纵坐标差值大于横坐标差值，由公式(6)可知此时为长轴参数，为短轴参数。当横、纵坐标差较大时，由公式(7)可知自适应椭圆距离在计算过程中发生数量级变化，从而增大距离差异性，进一步使得最小距离的差异显著，有利于策略图中聚类中心的准确判断。

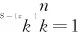
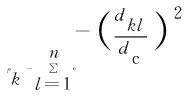
(8)

其中，表示式(4)所求的任意两点间的椭圆距离，表示截断距离。截断距离需要通过设置一个百分比来确定，取值一般为1%～2%，本文中取2%。确定截断距离前，需要先根据式(4)计算得到所有点的椭圆距离，做升序排列，过滤掉前2%的值，此时的最小值定义为截断距离。

计算各点密度后，需要根据密度来确定任意样本点的最小距离。这里的最小距离指的是，距离样本点最近且密度大于的样本点，此时两点的椭圆距离为的最小距离；若不存在密度大于的点，则找出距离最远的样本点，将此时的标记为最小距离，其数学表示为

(9)

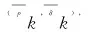
(10)

(11)

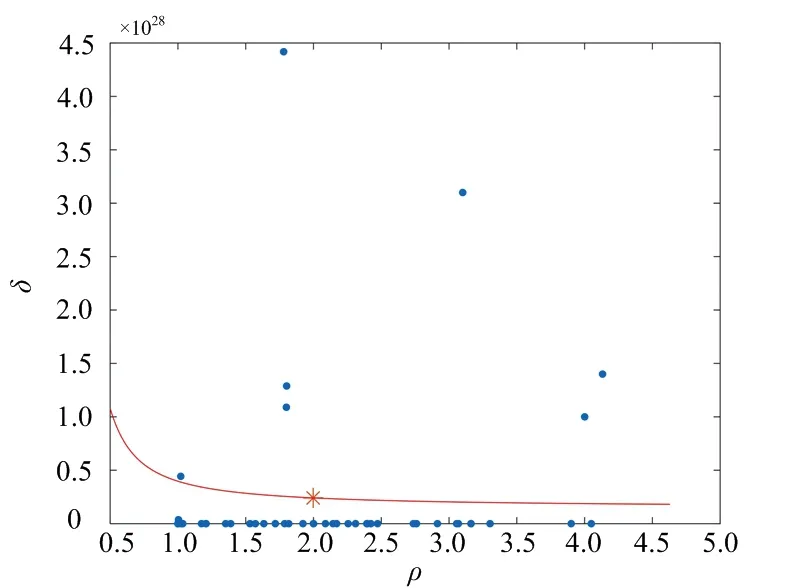
图2 加入幂函数曲线的决策图

由图2可容易确定位于曲线()上方的点满足密度大且最小距离大，即为所求的初始簇中心；位于曲线()下方的点为其他点，需要进一步做聚类处理。

2.2 结合速度的FCM算法

FCM算法是一种基于对目标函数优化的数据聚类算法，其聚类结果是每个样本点关于簇中心的隶属度和更新的簇中心。其中隶属度是一个模糊概念，表示的是某一样本点属于某簇的程度，取值范围为[0,1]，任一样本点关于所有簇中心的隶属度之和为1。在计算过程中隶属度和簇中心会不断更新，直至簇内加权误差平方和最小，得到最终的聚类划分。

(12)

由隶属度定义可知，任意样本点关于聚类中心的隶属度之和为1，即

(13)

(14)

式中‖-‖表示样本点集中第点到第个聚类中心的距离；表示模糊指数，其大小代表模糊程度，值越大表示分类的模糊性越大，反之越小，范围为[15,25] ，通常取2，在本文中亦取2。将式(14)结合约束式(13)，构造拉格朗日函数为

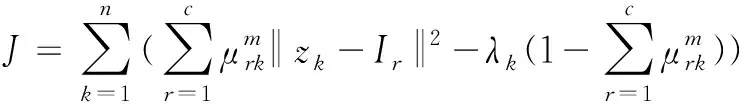
(15)

为求取目标函数的极值，需要将函数分别对和求偏导，并令偏导为0，即

(16)

求解式(16)得到式(17)，由式(17)关系式可知模糊隶属度与聚类中心之间存在一定的相关性，因此FCM算法的和初始值是十分重要的。

(17)

在计算迭代过程中，算法的目标函数值会不断变化，并最终趋于稳定。当更新的目标函数值与上一次的迭代值满足迭代停止条件时，结束计算，输出此时的、。迭代停止条件：

=-<

一是开展新进公务员培训。坚持每年对新录用公务员、转业干部等开展国土资源专业法律法规知识培训。以学法用法为载体，夯实国土干部法治理念。据统计，省厅每年举办各类培训班二十多期，这些师资主要来自各相关业务工作领域，由处室负责人或者业务骨干讲解，通过这种“传、帮、带”的教育培训，新进干部受益非浅，为他们及时转换角色适应工作打下了基础，反响较好。

(18)

式中，为设定的最小更新量，本文取0.000 1。最大迭代次数=1 000，此数值可根据实际情况调整，经实验验证，迭代次数一般在100以内，迭代结束便得到一次聚类结果。

在不断的实验中发现来自同一辆车的不同采样点速度差值极小，而来自不同车的速度差异明显。根据这一特性，结合一次聚类结果，使用模糊聚类的思想进行二次聚类以提高聚类精度。首先，提取每簇样本点的速度信息，确定每簇的速度中位数(=1,2,…，)。这里采用每簇的速度中位数而不使用均值是因为，经实验发现一次聚类结果中存在误判的点但数目不多，而同一辆车的采样点速度差值极小，因此选用中位数更具有代表性、更合理。利用一次聚类结果更新的，构造目标函数如下：

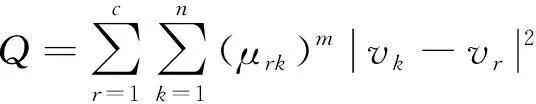
(19)

其中，模糊指标取2，将约束条件式(13)代入目标函数中，与一次聚类相同使用拉格朗日乘子法，解得最优解为

(20)

根据采样点的速度特征，设定此部分的迭代终止条件是，同一簇内任意两点间的速度差值小于，即

|-|<, ∀,且≠

(21)

满足式(21)终止迭代后，得到更新的，确定最终的聚类结果。本文实验中取05 m/s。最终，由两次模糊聚类得到的是在位置、速度上具有强相关的聚类结果。

综上，本文提出的一种改进的道路行车密度峰值模糊聚类算法具体步骤如下：

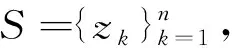
输出：更新的

a) 由公式(4)得到，并代入式(7)计算各点的密度，根据式(9)得最短距离；

c) 以为横轴，为纵轴画二维决策图，确定曲线()上方的点为初始簇中心；

d) 计算和各样本点到初始簇中心的距离，将二者作为初始值代入FCM算法进行迭代计算；

e) 迭代更新隶属度和聚类中心；

f) 重复e)，直至满足迭代终止条件式(18)，输出一次聚类结果和；

g) 提取各簇样本点的，确定簇内样本点的速度中位数；

h) 根据式(20)迭代更新和；

i) 重复h)，直至同簇内任意两点的速度满足式(21)时，迭代终止；

j) 输出更新的和，得到二次模糊聚类结果。

3 仿真实验

3.1 整体流程

本文采用77 GHz毫米波雷达，工作波形为线性调频连续波，其发射天线和接收天线都为4个，最大可同时探测128个移动车辆目标。采集过程中雷达工作参数如表1所示，每个场景采集10帧ADC原始数据，数据传输速率为20.1 Mbit/s。

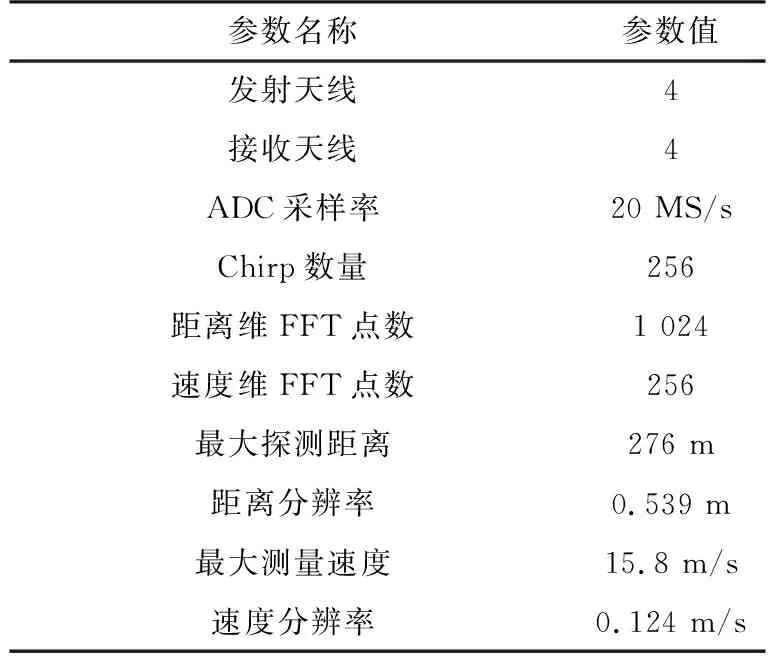
表1 雷达工作参数及理论性能

由表1参数可计算出一帧的数据量大小为发射天线×接收天线×距离维FFT点数×速度维FFT点数×2=8 192 Kbit。采集的数据为二进制格式，保存在“.dat”文件中，数据文件大小可以检验采集过程是否存在数据丢失。采集数据过程中有录像可以和算法处理结果进行对比。处理数据的环境为MATLAB R2018b，计算机运算条件为Windows 10， 64-bit，8G内存。

数据处理流程如下：

1) 将数据文件读入MATLAB经过傅里叶变换得到样本点的位置、速度信息；

2) 对得到的数据信息做滤波、恒虚警等处理滤除杂波；

3) 将去除杂波后的样本点位置、速度信息代入第三部分提出的算法中，经两次模糊聚类，得到最终高精度的聚类结果。

3.2 实验结果对比

为验证本文提出的算法，用雷达板在城市天桥上采集道路上行驶车辆的数据，对采集的原始数据经预处理后做聚类处理。本部分验证FCM算法、DBSCAN聚类算法和本文提出的聚类算法在3个不同场景下的聚类处理结果。

场景1： 多个小轿车相距较近。

以图3所示的道路场景1为对照，处理相应的雷达数据，图4给出了不同聚类算法对场景1的处理结果。其中，图4(a)给出了经滤波处理后的采样点，共53个。图4(b)为DBSCAN聚类算法处理结果，其中最小半径设定为2.2，簇内最小数目为3，共识别出6簇数据。图4(c)为FCM算法处理结果，最终得到7簇数据和各簇中心。图4(d)为DPC算法处理结果，由策略图确定初始聚类中心后，根据各点到聚类中心的距离进行分类，共得到3簇结果。图4(e)为本文提出的算法处理结果，得到7簇数据和各簇中心。

图3 道路场景1

图4 不同聚类算法对场景1的处理结果

对比图4(b)和图4(c)可知，DBSCAN算法和FCM算法能区分大部分车辆目标，但均不能区分位于道路前方相距很近的两辆车。图4(d)由于聚类中心数目误差较大，不能正确聚类道路车辆。由图4(e)可知，本文提出的算法能很好地区分车辆目标，聚类正确。

场景2： 公交车与小轿车相距较近。

以图5所示的道路场景2为对照，处理相应的雷达数据。图6给出不同聚类算法对场景2的处理结果。其中，图6(a)是经滤波处理后的采样点，共39个。图6(b)为DBSCAN聚类算法处理结果，最小半径设定为2.5，簇内最小数目为3，共识别出5簇数据。图6(c)为FCM算法处理结果，最终得到6簇数据和各簇中心。图6(d)为DPC算法处理结果，共识别出3簇数据。图6(e)为本文提出的算法处理结果，得到5簇数据和各簇中心。

图5 道路场景2

图6 不同聚类算法对场景2的处理结果

图6(b)中DBSCAN聚类算法的参数比场景1中参数大，是为了兼顾大目标，但从聚类结果可知，由于公交车目标过大，分布稍远的点会被归为噪声点，影响聚类正确率。图6(c)中FCM算法将公交车大目标分为了两个小目标，图6(d)为DPC算法不能正确聚类道路车辆，簇数目相比其他算法误差最大，而本文提出的算法如图6(d)所示，可以做到正确聚类。

场景3： 多个小轿车相距较近，公交车与小轿车相距较近。

以图7所示的道路场景3为对照，处理相应的雷达数据。图8给出了不同聚类算法对场景3的处理结果。其中，图8(a)给出了经滤波处理后的采样点，共58个。图8(b)为DBSCAN聚类算法处理结果，其中最小半径设定为2.5，簇内最小数目为3，共识别出6簇数据。图8(d)为DPC算法聚类结果，共识别出4簇数据。图8(c)和图8(e)分别为FCM算法、本文提出的算法处理结果，均得到8簇数据和各簇中心。

图7 道路场景3

图8 不同聚类算法对场景3的处理结果

对比图8(b)和图8(c)可知，DBSCAN算法和FCM算法能区分大部分车辆目标，但均不能区分位于道路前方相距很近的两辆车。图8(d)的DPC算法由于聚类中心的判断错误，导致最终聚类结果效果差。由图8(e)可知，本文提出的算法能很好地区分车辆目标，聚类正确。

图8(b)中DBSCAN聚类算法对于相距较近的小轿车容易聚类成一个目标，并且由于半径的限制，不能完整识别出场景中的公交车大目标。由图8(c)可知，FCM算法能够识别出各个车辆，但仍存在个别误判的样本点，精确度不够。DPC算法对于相距较近的车辆样本点聚类效果差。本文提出的算法在FCM算法的效果上做出优化，能够识别公交车的全部样本点，减少了误判的样本点。

根据以上3个特殊场景的聚类结果对比可知，DBSCAN聚类算法根据密度分类时，对相距较近和目标较大的车辆聚类效果较差。同时，受半径参数的约束，不能在兼顾小目标的前提下完整识别大目标。传统FCM算法聚类精度较高，能基本识别出道路上的大小车辆目标，但会有个别样本点的误判。DPC算法的初始聚类中心的确定存在误差，导致最终结果误差较大。本文提出的算法在FCM算法的基础上使用速度对数据点再次聚类，明显聚类效果更好。

最后，用指标来衡量各个算法的聚类准确度，定义为

(21)

式中，表示第簇中正确聚类的采样点个数，表示簇的总个数，表示处理的原始采样点个数。取值越高说明聚类准确度高，值为1时说明聚类结果完全准确。图9给出了选取的100帧采集数据，使用5种聚类算法的聚类精度比较，其中改进的FCM算法指本文提出的一次模糊聚类算法，即不作二次模糊聚类处理。由图9可以看出，改进的FCM算法比FCM算法聚类精度高，但存在不稳定的问题，本文提出的算法在真实公路场景中聚类精度更高且效果最稳定。

图9 各聚类算法的聚类精度比较

同时对上述实验的3个场景的算法运行时间进行比较，每个场景分别用DBSCAN算法、FCM算法、DPC算法、改进的FCM算法和本文所提算法运行100次，求取运行时间平均值，时间比较如表2所示。

表2 算法运行时间比较

由表2可知，本文提出的算法使用DPC算法初始化后再做模糊聚类使得时间复杂度增加，耗时相对较长，但在场景3数据较大的情况下，本文所提算法与各算法处理时间接近。同时，本文采用结合速度信息的二次模糊聚类处理，用较小的时间消耗获取更高、更稳定的聚类正确率。因此本文所提算法可以解决相邻车辆聚类结果不准确的问题，具有更高的准确度，在之后的工作中需要优化算法减少运行时间，使其在时间上具有明显优势。

4 结束语

本文提出的算法根据道路场景的车辆毫米波雷达数据特征，首先，使用改进的DPC算法，采用自适应椭圆距离绘制决策图，找出密度峰值点确定为初始聚类中心。接着，根据初始聚类中心计算初始隶属度矩阵，将二者代入FCM算法中，迭代计算得到一次聚类结果。最后，根据道路中每辆车的速度信息特点，构造关于速度的模糊目标函数，对一次聚类结果进行修正，迭代计算得到最终的聚类结果。实验结果表明，本文算法能有效解决城市道路车辆相距很近导致的目标聚类存在较大误差的问题，具有精度高、鲁棒性强的优点。