空间目标雷达轨道改进原理及工程实现
2022-10-26黄晓斌
黄晓斌, 张 燕, 鲁 力, 肖 锐
(空军预警学院, 湖北武汉 430019)
0 引言
雷达的优点是白天黑夜均能探测远距离的目标,且不受雾、云和雨的阻挡,具有全天候、全天时的特点,并有一定的穿透能力。雷达已广泛应用于社会经济发展(如气象预报、资源探测、环境监测等)和科学研究(天体研究、大气物理、电离层结构研究等)中,但其应用最广的还是军事领域,如防空警戒、反导预警、空间监视、指挥引导等。
空间目标监视雷达是空间监视领域的骨干装备,与常规防空雷达相比,主要增加了空间目标轨道确定功能,轨道改进实现该功能的核心模块,轨道改进模块的研制涉及非常复杂的航天动力学知识,这对从事雷达系统设计的非轨道力学专业的研究人员来说带来极大困难。虽有一些开源定轨软件可供借鉴,但这些软件主要用于处理光学观测数据,并不适合处理雷达观测数据。为此,作者着手开发RadarOrbDet函数库来辅助非轨道力学专业的人员进行空间目标监视雷达的系统设计,目前已完成坐标转换模块、初轨确定模块和摄动分析模块的开发,本文研究轨道改进模块的开发。
轨道改进是空间目标轨道确定的重点和难点,它涉及的内容较多,包括摄动分析、偏微分方程的变分法分析、最小二乘优化等理论,本文聚焦空间目标雷达定轨中的批处理轨道改进问题,着重介绍了最小二乘轨道改进原理,讲解了模型中的偏导数求解方法,描述了程序实现流程,最后用ODTK软件验证了本文软件设计的有效性。
1 最小二乘轨道改进原理
最小二乘轨道确定的基本原理是找到一条轨道,使得理论观测值和实际观测值之间的残差平方和(即损耗函数)最小,即求解,使得式(1)的值最小。
()=[-()][-()]
(1)
式中:=[();()]是卫星在时刻的位置和速度构成的状态参量,由通过轨道预报可以得到一条参考轨道;=[;;…;]是次雷达实际观测矢量,每次观测矢量包含距离、方位和俯仰三个分量(,,);()是由参考轨道计算得到的理论观测值。
由于是一个非线性函数,式(1)描述的是一个非线性最小二乘问题,求解异常困难,通常采用泰勒展开将其转化为一个线性最小二乘问题,然后通过迭代方式求解它的线性最小二乘近似解,表达式为
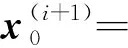

(2)

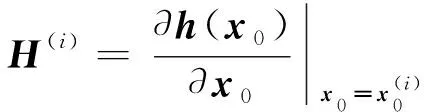
(3)
2 模型中的偏导数求解
式(2)的求解关键在于偏导数雅克比矩阵的计算,不失一般性,以某一时刻的雷达观测量为例。为书写方便,除时刻外,省略其他时刻索引。
利用求导链式法则,转换为
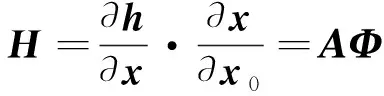
(4)
式中,矩阵是当前时刻观测量对当前状态参量的偏导数矩阵,是当前时刻状态参量对初始时刻状态参量的偏导数矩阵,也称为状态误差传递矩阵。
2.1 观测偏导数矩阵求解
在忽略光行差等因素后,雷达观测量只与卫星当前的位置有关,而与其速度无关。因此,矩阵可拆分成
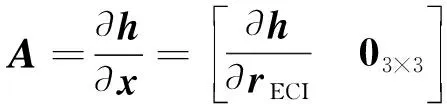
(5)
式中,是卫星在惯性坐标系(ECI坐标系)下的位置矢量。
雷达观测是基于站心地平坐标进行的(如南-东-天坐标系,SEZ),直接计算观测量对ECI坐标系下的位置矢量的偏导数比较困难,因此,矩阵的计算需进一步运用链式求导法则进行分解:
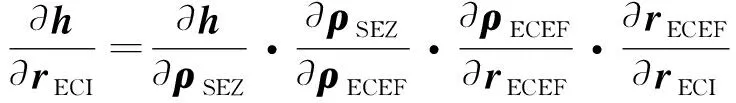
(6)
式中,是卫星在SEZ坐标系下的直角坐标,用(,,)表示;是雷达对卫星的观测矢量在地固坐标系(ECEF坐标系)下的表示;是卫星在ECEF坐标系的位置矢量。
注意到
=-
(7)
式中是雷达在ECEF坐标系下的位置矢量,是个常矢量。
因此
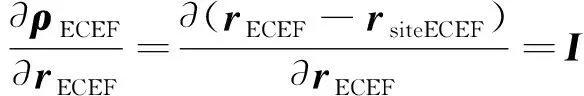
(8)
根据坐标变换有

(9)

根据式(9)有
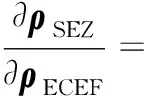
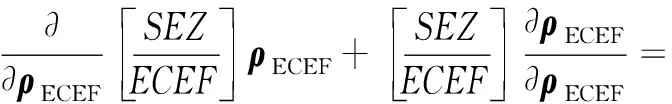

(10)
同理有
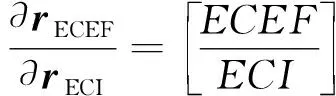
(11)
将式(8)、(10)和(11)代入式(6)有
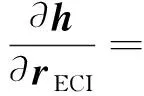
(12)
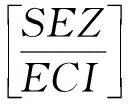
在坐标系下,由直角坐标和极坐标的关系,易得

(13)
将式(13)代入式(12),有
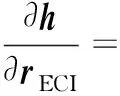

(14)
计算式(14)中的两个矩阵时,都需要在当前观测时刻进行。最后,将式(14)代入式(5)后,可得矩阵。
2.2 状态误差传递矩阵求解
设卫星的运动方程为

(15)
则

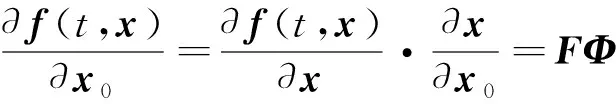
(16)
其中,矩阵为

(17)
由于采用迭代方式进行最小二乘问题求解,因此对矩阵的求解精度要求不高,从而对矩阵的求解精度也要求不高。因此,矩阵中的加速度可以只考虑地球中心引力和低阶的非球形引力摄动,以加快计算机求解速度。
在只考虑地球引力(包含非球形摄动)情况下,加速度只与位置有关,而与速度无关,并且它的计算通常是在ECEF坐标系下进行,具体表达式可以参考文献[18],篇幅所限,这里不再赘述。
最后还需将ECEF坐标系下的偏导数矩阵转换到ECI坐标系下。在忽略科里奥利力和离心力情况下,有如下关系式:

(18)
计算得到当前时刻的矩阵后,采用数值微分方程方法求解。
3 程序设计
图1是最小二乘轨道改进算法的程序设计流程图。
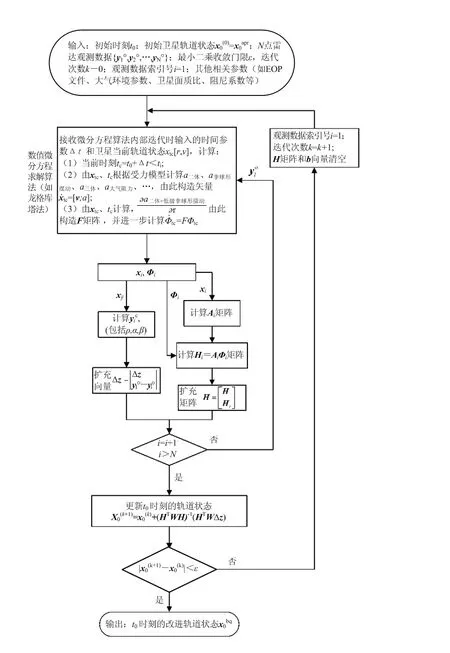
图1 最小二乘轨道改进算法的程序设计流程图

程序分为三层循环,第一层循环是数值微分方程求解的内部循环,输出结果是第时刻的参考轨道和状态误差传递矩阵;第二层循环是遍历每个观测值,根据最小二乘原理求解单次轨道改进量;第三层循环是执行多次最小二乘轨道改进,使最终结果趋近于实际轨道状态。
4 仿真实验
4.1 接口调用示例
采用C语言按照第3部分的程序设计原理实现了最小二乘轨道改进的接口函数rodLeastSquare,并集成到RadarOrbDet库中。rodAccelHarmonic接口函数的软件调用方法如图2所示。

图2 最小二乘轨道改进接口函数说明
4.2 实验比较
在STK11.2中仿真一颗卫星,其历元轨道参数设置如表1所示,运动模式设置为HPOP(高精度轨道预报),考虑21阶非球形摄动。雷达站址的经纬高为(120°,30°,0)。选择2021-09-07 19:15:01至2021-09-07 19:15:10间隔1秒的10点数据,对距离、方位和俯仰分别加上100 m、01°和01°的观测误差。

表1 卫星轨道根数
采用本文软件和AGI公司开发的一款先进的轨道确定与分析软件——Orbit Determination Tool Kit(ODTK)进行定轨比较,ODTK与本文软件计算结果如表2所示,采用式(19)所描述的位置和速度相对误差进行定量比较。
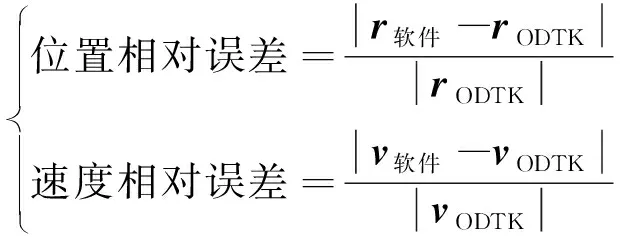
(19)
从表2可以看出,定轨的位置误差为0.059 6%,速度误差为0.35%,表明本文软件算法是有效的,其误差主要来源为计算程序的坐标与时间转换、计算截断误差等。

表2 定轨结果对比表(ODTK与本文软件)
5 结束语
本文针对空间目标雷达定轨中的批处理轨道改进问题,介绍了最小二乘轨道改进的原理,描述了模型中的偏导数求解,给出了程序设计思路,仿真表明了软件设计的有效性。此外,本文开发的RadarOrbDet函数库可以很好地辅助空间目标监视雷达系统设计人员进行定轨指标的快速设计和验证。
