基于微分方程模型的中国天然气消费量预测

2022-10-25辛俊萱杜荣杰

煤气与热力 2022年10期

沈威，辛俊萱，杜荣杰，乔亮

(深圳市燃气集团股份有限公司，广东深圳518049)

1 概述

近年来，天然气表观消费量从2006年的不到600×108m3激增到2021年的3 726×108m3[1]。表1是中国2000—2021年天然气表观消费量(简称消费量)和增长率，除个别年份由于客观因素影响导致增长率较低(如2015年)外，其他年份均保持了较高的增长率，2000—2019年的年复合增长率为14.23%，2020年受新冠疫情的影响，天然气消费量增长略有下降，但到2021年又出现了强劲反弹。

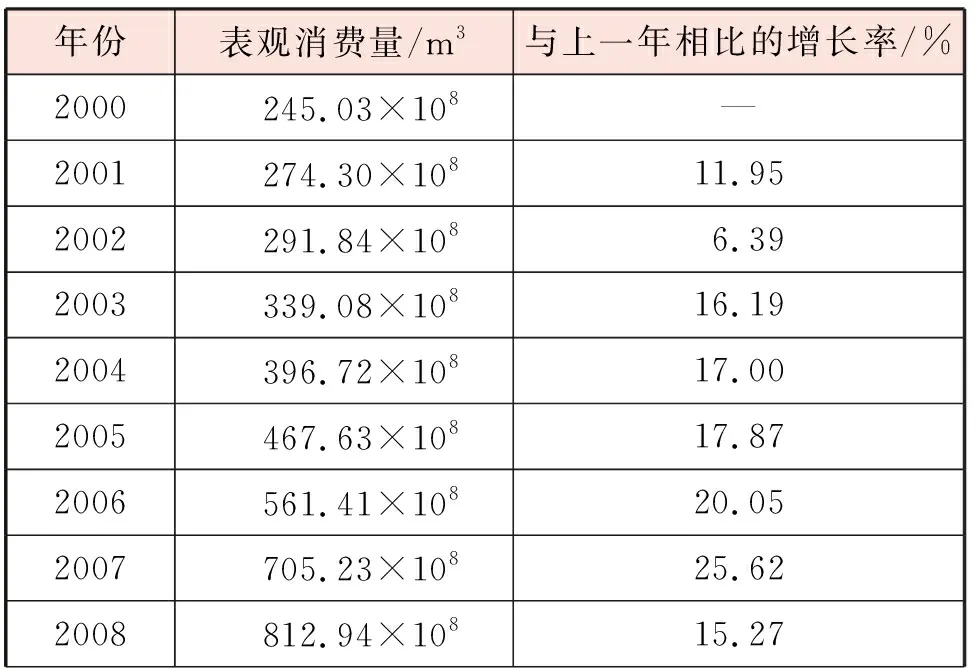
表1 中国2000—2021年天然气表观消费量和增长率

续表1

2003—2013年，是天然气行业发展的黄金10年，天然气消费量年复合增长率达到17%，即使在2009年金融危机当年，天然气消费量仍实现了10.12%的增长，高增速主要来自国内城镇化建设的推进以及持续高位的房地产投资拉动，城镇居民用气量10年来增长4倍，用于城市供电调峰的天然气发电项目用气量累计增21倍。与此同时，基于低价化工用气的企业也拉动制造业天然气消费量累计增3倍。

2014年以后，因为天然气气价改革，天然气价格出现连续上调，由于经济增长放缓，下游工商业用气消费量增速明显回落，主要燃气运营商销气量增速降至2015年的12%以下。虽在2015年末天然气价格一次性下调0.7元/m3，但消费量增速恢复并不明显。2016年后在能源改革深化以及环保趋严的驱动下，燃气行业实现了二次成长。2016年9月，发改委加快油气体制改革进度，出台一系列规范、监管中游管网价格文件，“放开两头管中间”，中游管道资产收益率控制在8%，降低过高的中间收费环节，进一步降低终端用气价格。同时，京津冀、长三角、珠三角环保要求趋严，禁煤区及限煤区大规模补贴煤改气项目，天然气消费量增速自2017年2月开始明显回升。2016—2019年，城镇化、煤改气带来居民用气、天然气发电消费量快速增长，制造业消费量回暖，天然气出现温和复苏迹象，2016—2019年天然气消费量复合增速在14%左右。

本文模型均根据2000—2019年天然气消费量数据建立，对2000—2019年天然气消费量进行拟合，对2020—2021年的天然气消费量进行预测，预测结果与实际数据比较，计算得出相对误差。本文天然气消费量均指年消费量，均取2000年为t=0。

2 天然气消费量指数函数模型

2.1 简单指数函数模型

已知今年的天然气消费量为V0，过去20年的年复合增长率为ra，那么今后第k年天然气消费量的简单指数函数模型为：

Vk=V0(1+ra)k

(1)

式中Vk——今后第k年天然气消费量，m3

V0——今年天然气消费量，m3

ra——过去20年的年复合增长率

此模型的局限性很大，要求年复合增长率在今后k年内保持不变。

2000—2021年天然气消费量真实曲线、简单指数函数模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线见图1。2000—2019年天然气消费量拟合值与真实值的平均相对误差为7.23%，2020—2021年天然气消费量预测值与真实值的平均相对误差为7.63%。

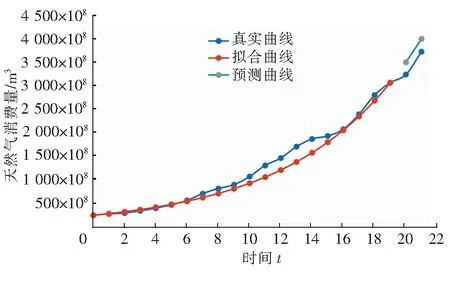
图1 2000—2021年天然气消费量真实曲线、简单指数函数模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线

2.2 指数函数模型

取中间变量x，有天然气消费量计算公式：

V=108x

(2)

式中V——天然气消费量，m3

x——中间变量

当考察一个国家或者地区天然气消费量随时间连续变化的规律时，可以将天然气消费量看作连续时间(年份)t的连续可微函数。记初始年份(t=0)的x为x0，假设年增长率为r，rx就是单位时间内的增长量，于是得到微分方程和初始条件。

微分方程：

(3)

式中t——时间(年份)

r——年增长率

初始条件：t=0时,x=x0

对式(3)积分得：

x=x0exp(rt)

(4)

r>0时，天然气消费量将按照指数规律无限增长。

基于式(4)，根据表1中2000—2019年天然气消费量数据，用MATLAB编程计算，利用最小二乘法得x0=252.08，r=0.134 9，拟合优度为0.987 7。则天然气消费量指数函数模型为：

x=252.08exp(0.134 9t)

(5)

2000—2021年天然气消费量真实曲线、指数函数模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线见图2。2000—2019年天然气消费量拟合值与真实值的平均相对误差为2.03%，2020—2021年天然气消费量预测值与真实值的平均相对误差为15.24%。

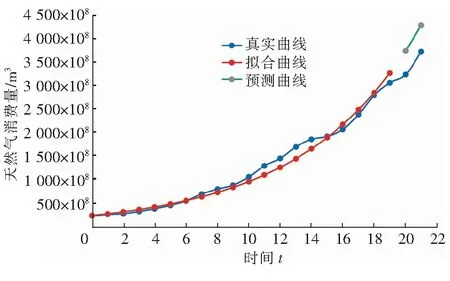
图2 2000—2021年天然气消费量真实曲线、指数函数模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线

2.3 改进的指数函数模型

为显示增长率随时间变化的规律，将年增长率r视为时间t的函数。表1中2001年(t=1)至2019年(t=19)的年增长率曲线以及年增长率与时间的拟合曲线见图3。

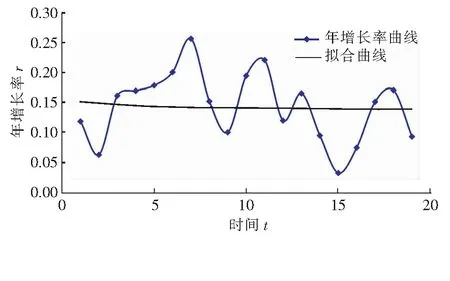
图3 2001—2019年年增长率曲线以及年增长率与时间的拟合曲线

由图3可以看出，年增长率变化非常大，但总体处于微下降趋势，年增长率与时间的拟合曲线方程为：

r=-0.009lnt+0.158 6

(6)

由式(3)得：

t=1时，x=x1

(7)

解该微分方程得：

x=x1exp(-0.009tlnt+0.167 6t-0.167 6)

t≥1

(8)

由表1可知x1=274.3，得到改进的指数函数模型为：

x=274.3exp(-0.009tlnt+0.167 6t-

0.167 6)t≥1

(9)

2000—2021年天然气消费量真实曲线、改进的指数函数模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线见图4。2000—2019年天然气消费量拟合值与真实值的平均相对误差为1.89%，2020—2021年天然气消费量预测值与真实值的平均相对误差为13.06%。

图4 2000—2021年天然气消费量真实曲线、改进的指数函数模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线

3 天然气消费量logistic模型

3.1 微分方程的建立

在分析天然气消费增长率时，需要考虑天然气消费的增长刺激因素和天然气消费的抑制影响因素。天然气消费增长刺激因素有经济增长、煤改气政策等，天然气消费抑制影响因素包括经济增长放缓、人口规模增长放缓以及可再生能源的替代[2]。如果同时考虑诸多因素影响，问题必然十分复杂，为简化问题，我们认为，在天然气消费量较小时，消费量的驱动发展较快，r随x增加而增大；在天然气消费量达到一定水平时，r随x增加而减小。因此认为天然气年增长率为一个以天然气消费量为自变量的线性函数，记为：

r=a+bx

(10)

为赋予系数a、b以实际含义，在此引入两个参数：

① 天然气内禀增长率r0。r0是天然气消费量为0时的理论增长率，则有a=r0。

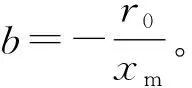
由此得到年增长率的函数为：

(11)

由式(3)得微分方程：

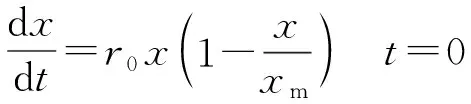
(12)

微分方程(12)可用分离变量的方法解得logistic模型：

(13)

3.2 logistic模型参数的估计

对式(13)取倒数，用2000—2019年天然气消费量进行拟合，用MATLAB软件非线性最小二乘法编程得到参数x0=255.92，xm=6 839.04，r0=0.157 3，拟合优度为0.987 6。则微分方程(13)的最终形式，即logistic模型为：

(14)

2000—2021年天然气消费量真实曲线、logistic模型2000—2019年天然气消费量拟合曲线及2020—2021年天然气消费量预测曲线见图5。2000—2019年天然气消费量拟合值与真实值的平均相对误差为0.73%，2020—2021年天然气消费量预测值与真实值的平均相对误差为-2.96%。可以看出，相比其他模型，logistic模型预测最为准确。