基于POD-RBFN降阶模型的串列叶栅流场预测
2022-10-25尚珣刘汉儒杜亦璨胡之颉
尚珣,刘汉儒,杜亦璨,胡之颉
(1.西北工业大学 太仓长三角研究院,太仓 215400)(2.西北工业大学 动力与能源学院,西安 710129)
0 引言
随着现代航空发动机对压缩系统载荷、性能、稳定裕度提出的要求越来越高,传统的单叶片设计已经逐渐无法满足现代压气机的需求。串列叶片作为一种被动的流动控制技术,因其结构简单、便于工程应用等特点而得到广泛关注。在研究串列叶型优化设计时,通常采用数值模拟的方法,但对于串列叶栅这种流场结构较复杂或存在多个设计变量的优化问题,传统CFD所需要的计算成本往往是不可接受的。为了快速确定气动参数的函数响应,提高优化设计效率,降阶预测模型应运而生。
本征正交分解(Proper Orthogonal Decomposition,简称POD)方法是一种高效的数据降维分解方法,可以提取出数据的主导模态,因此可以用于流场分析及降阶预测模型的构建。例如,Duan Y等对Gappy POD降阶方法进行了研究,将其用 于 叶 型 的 优 化 设 计;Gong Helin等对Gappy POD降阶模型进行了进一步发展,提高了方法的稳定性,并将其应用于功率分布的预测。然而,Gappy POD是通过线性响应POD基函数来实现数据填充预测的,这虽然使其具有简单高效、可以同时响应多个输出参数等优点,但其对于强非线性响应问题是无效的。
近年来,神经网络方法逐渐得到了流体力学领域研究者们的关注。例如,Zhu Linyang等将径向基函数神经网络(Radial Basis Function Network,简称RBFN)用于湍流模型的构建,实现了涡黏的预测;Sun Gang等使用翼型数据库训练人工神经网络,实现了翼型/机翼的快速反设计。在流体力学研究中,流场信息在流动机理分析时是不可或缺的。考虑到流场信息的维度较高,将神经网络方法直接用于复杂流场信息的获取会产生维度灾难问题,因此需要先降低流场的维度,POD方法就是一种不错的选择,且已经在叶轮机械内流领域得到了应用。例如,H.Kato等基于POD方法构建代理模型,并将其应用于涡轮几何外形优化;李春娜等采用基于POD-BPNN的代理模型实现了翼型的快速反设计。综上所述,现有研究大多是通过几何与气动参数的一一对应关系,实现变几何的性能预测或变性能参数的几何反设计,鲜有研究关注非定常流场的演化过程。
POD流场降阶需要基于一定的样本流场来进行,且原始样本的选择直接影响着流场的降阶质量,进而影响后续降阶模型的预测精度。目前各学科常用的静态抽样方法包括随机抽样、均匀抽样、拉丁超立方抽样等,但静态抽样方法只考虑了样本在采样区间中的空间分布,因此当采样区间中的样本质量及敏感性程度分布不均匀时,静态抽样方法就无法取得令人满意的结果。近年来,基于函数响应偏差的自适应抽样方法已得到迅速发展,该方法在进行采样时考虑了样本对于需求的敏感性,通过函数响应偏差确定敏感空间,因此能够有效提高抽样效率与样本质量。
本文以串列叶栅为研究对象,结合POD方法的流场降阶能力和径向基函数神经网络可以响应强非线性问题的特性,构造POD-RBFN混合降阶模型,以实现串列叶栅非定常流场的快速预测;而后将基于函数响应偏差的自适应抽样方法应用于降阶模型初始样本的获取,以提高降阶模型的采样效率。
1 数值方法
1.1 网格及计算设置
本文选取J.Eckel等设计的高载荷压气机串列叶栅为研究对象,叶栅几何及主要参数分别如表1和图1所示。该串列叶栅前后两个叶片弦长均为31.5 mm,整体弦长62.4 mm,设计工况气流转折角为50°,前后两个叶片的设计载荷相等。
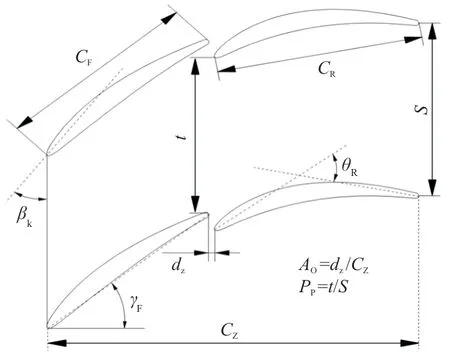
图1 叶栅几何示意图Fig.1 Geometric description of tandem cascade

表1 串列叶栅几何参数Table 1 Geometric parameters of tandem cascade
采用AutoGrid 5软件生成计算网格,前、后叶片网格均采用H-O-H结构拓扑。叶栅进口段计算域延伸2倍弦长,出口段延伸2.5倍弦长。壁面附近网格进行加密处理,以保证近壁面第一层网格y值小于1。最终计算网格总数为39 896,此时网格正交性、延展比、长宽比均已满足计算要求。叶栅通道及局部网格示意图如图2所示。

图2 网格示意图Fig.2 Schematic diagram of single-channel grid
为了对网格独立性进行验证,本文对三套网格(Mesh1,Mesh2,Mesh3)进行对比,网格数分别为22 480,39 896,79 906。0°攻角、来流马赫数0.6工况下的叶表静压升系数(C)分布如图3所示,横轴z为垂直于栅距方向的距离。C的定义为C=(P-P)/(P-P),其 中P为 静 压,P为 进 口 静压,P

图3 叶表静压升系数分布图Fig.3 Tandem cascade CP distribution
*为进口总压。
从图3可以看出:随着网格数量的增大,Mesh1的静压升系数整体略微偏大,而Mesh2与Mesh3的静压升系数分布基本一致。综合考虑计算精度与计算效率,本文采用Mesh2进行后续研究。
采用CFX-Solver进行流场数值求解。进口边界条件给定总温为288.15 K,总压为101 325 Pa。叶片表面采用无滑移边界条件和绝热壁面条件,上、下两个边界为周期性平移边界。通过调节进口轴向和节距方向气流速度分量来实现不同的气流攻角,调节出口平均静压保证进口马赫数为0.6。采用SST两方程湍流模型,以实现对流场细节较为准确地捕捉。非定常计算采用URANS方法,物理时间步长为2×10s,每个时间步进行10次内迭代。将定常计算结果作为非定常计算的初场以节省计算时间。
1.2 POD及RBFN理论
早期POD的奇异值分解需要定义域中的所有解集,这使得其在特征值的求解及系统稳定性方面均表现欠佳,从而难以在工程中应用。直到快照POD方法的提出,改善了计算量及稳定性方面的问题,POD方法才逐渐被应用于各个领域。快照POD的基本原理如下:
首先根据一组解集得到快照矩阵U=[u,u,…,u],矩阵中每一个元素均为一个流场解。然后对矩阵进行去中心化处理:

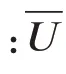
POD方法的核心工作就是寻找一组最优正交基Φ=[φ,φ,…,φ],以及与之对应的基系数矩阵A=[a,a,…,a],使得其中的元素满足:

快照脉动矩阵的最优正交基可通过求解如下最优值问题得到:
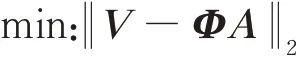
使用奇异值分解(SVD)求解该最优值问题。获取最优正交基Φ后,将各个流场快照分别映射到Φ上,得到与各个初始流场解对应的基系数a。
按照基模态“能量”的定义,对基模态进行排序。前几阶模态包含了流场中的大部分“能量”,因此使用较少的模态阶数即可实现原始流场的降阶重构。某一阶基模态的“能量”定义为

式中:λ为自相关矩阵R(R=VV)的第i个特征值。
求解得到最优正交基Φ之后,原始流场可以根据系数矩阵A及式(2)精确重构。因此,如果可以得到某非样本流场解对应的系数向量,就能根据已知的正交基Φ对该流场进行预测。
非样本流场POD系数的响应通常采用线性方法,但考虑到流场时空演化中可能存在的非线性规律,本文采用径向基函数神经网络来响应POD系数。径向基函数神经网络(RBFN)是由D.S.Broomhead等提出的一种收敛快、结构简单,且对非线性系统具有一致逼近性的神经网络。RBFN是经典的三层前向网络,第一层为输入层,第二层为隐藏层,第三层为输出层。隐藏层使用径向基函数作为激活函数的神经元。
至此,POD-RBFN混合模型构建完成,该降阶模型可以根据一组同类型的流场解集(可以是同一几何在不同工况下的流场解,也可以是同一工况下不同叶型几何参数的流场解)获取流场基模态,并对目标流场(非样本流场)的POD系数进行非线性响应,从而实现目标流场的预测。本文的混合预测模型是通过编写计算机程序实现的。
1.3 自适应抽样方法
在降阶模型重构过程中,原始样本流场的质量直接影响POD基的生成,进而影响重构精度。为了提高获取的POD基的稳定性,考虑采用自适应抽样方法获取原始样本流场。近年来,基于函数响应偏差的自适应抽样方法已得到迅速发展,故本文采用四叉树法进行原始样本抽取。四叉树法自适应抽样的基本原理为:首先将样本空间中的边界角点、空间中心点、子空间中心点作为初始样本集;其次通过计算子空间中心点的函数响应偏差来确定目标子空间;然后在目标子空间中抽取其下一代子空间的中心点,并将其增加到初始样本集中;最后在新样本集中重新确定目标子空间。重复该步骤,直到最终所有采样点的响应偏差均满足要求或总样本数目满足要求。
这一过程中的函数响应偏差由式(4)计算得到:

式中:E(u)为第i个流场快照u的响应偏差;D(u)为第i个流场样本u与其他样本之间的相关性强弱。
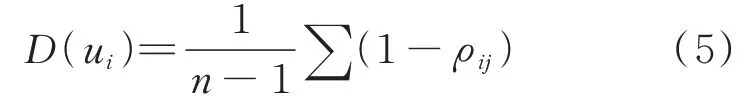
式中:n为样本总数,代表样本集合中第i个样本流场与第j个样本流场之间的线性相关性系数。
式(5)的含义为,样本流场u与其他样本流场的不相关性(1-ρ)的均值,相关性越强则D(u)越小。
流场快照u的响应偏差E(u)是由“弃一法”(Leave-one-out,简称LOO)交叉验证得到的。该方法的基本原理为:首先从初始快照集中去除掉样本快照u,然后基于剩余样本对缺失样本u进行预测,预测得到流场的整体误差即为该样本流场快照的响应偏差。
综上可知,如果某一个样本与其余样本的相关性越强,或者该样本的响应偏差越小,则说明该样本对于生成POD基及流场重构的贡献不大,而计算得到的该样本的函数响应偏差也就越小。因此可以根据函数响应偏差的大小来确定目标子空间。编写计算机程序并与上文得到的降阶模型进行适配,最终完成采用自适应抽样的POD-RBFN降阶预测模型的构建。
2 结果与讨论
2.1 CFD计算结果
首先通过定常数值模拟对该串列叶栅的气动特性进行研究。分别在进口一倍弦长和出口0.5倍弦长处设立计算面,计算得到的叶栅压比、损失攻角特性曲线如图4所示,左边纵轴P为叶栅的静压比,右边纵轴ω为叶栅损失系数,图中灰色圆点为实验所测得的叶栅损失。从图4可以看出:随着进口气流攻角的增大,叶栅静压比呈现出先增大,后急剧减小的趋势;而叶栅损失系数ω的变化趋势则大致与P变化趋势相反。这是因为随着气流攻角的增大,叶盆分离流动逐渐减弱,故此时静压比逐渐增大,损失逐渐减小;而当气流攻角进一步增大,此时会在叶片背面发生气流分离,使得流场恶化,静压比急剧减小,且损失急剧增大。
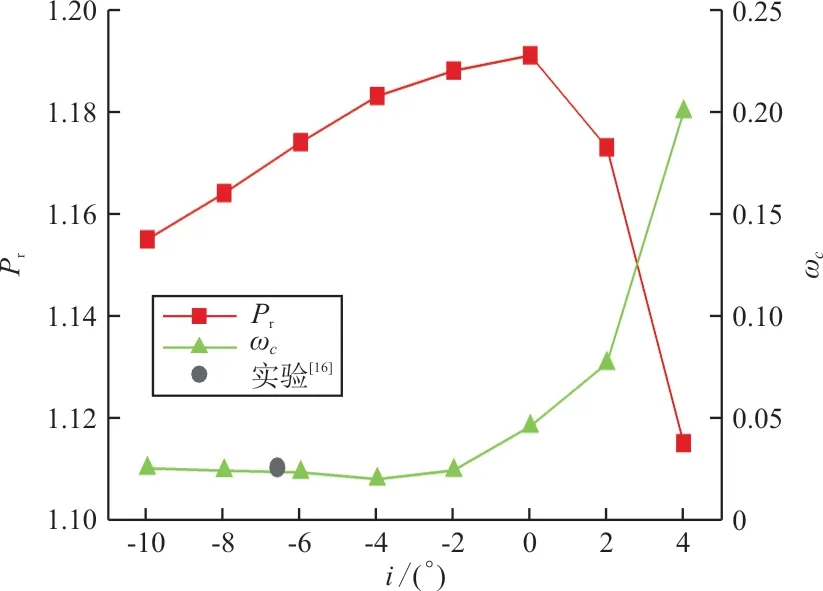
图4 叶栅攻角特性Fig.4 Incidence characteristic of tandem cascade
综合考虑不同攻角下的两种参数值,可知该串列叶栅在攻角[-10°,4°]范围内,当攻角为-2°时的气动性能最佳,而在攻角为4°时性能最差。为了突出流场中叶背分离流动的不稳定流动特征,对大攻角分离工况下的流动机理进行研究,选择2°攻角工况开展后续研究。
非定常计算得到的叶片附近流场马赫数云图及流线分布如图5所示,可以看出:在较大的气流攻角下,叶背的大范围分离流动主要发生在前叶片。这是由于一方面,与常规单列叶栅相比,串列叶栅单个前叶片的弦长较短且气流转折角较大,使得前叶片更易发生分离;另一方面,由于前、后叶片间隙射流的存在,前叶片尾缘分离产生的低能流体不易与后叶片气流发生掺混作用,从而使得前叶片的分离更为严重。与前叶片相反,由于串列叶栅缝隙射流的吹除作用,后叶片一直处于一个较为稳定的来流条件,故未发生明显的分离流动。

图5 流场马赫数及流线分布Fig.5 Mach number and streamline
2.2 POD流场分解
非定常数值计算得到的通常是一组离散时刻的流场解,而两个时刻之间的流场时空演化规律可能是非线性的,因此若想获得某非结果时刻的流场解时,采用简单的线性插值可能是不准确的。通过对串列叶栅非定常流场解的预测,来验证构造出的POD-RBFN混合模型的准确性。
当非定常计算整体残差稳定在0.000 01以下,且进、出口流量随时间小幅周期性波动时,认为此时计算已经收敛,保存100个连续时间步的非定常流场解作为原始样本集合,相邻时间步的时间间隔为0.000 02 s。本文使用流场涡量分布构造流场快照矩阵,对流场快照矩阵进行POD分解,得到相应的POD基函数和与之对应的POD系数。
通过求解自相关矩阵R的特征值λ,将特征值按照大小排列。这样就可以根据式(3)得到各阶POD基模态的“能量”占比,进而可以确定前多少阶模态可以包含原始流场中的绝大部分信息。计算得到的前10阶POD基模态所占流场的能量份额,以及前n阶模态总能量份额的大小如表2所示。前30阶各阶POD基模态所占能量份额的变化趋势如图6所示,横坐标为基模态的阶数,纵坐标为对数形式的各阶模态所占能量的比例E。

图6 各阶模态能量分布Fig.6 Energy distribution of each POD mode
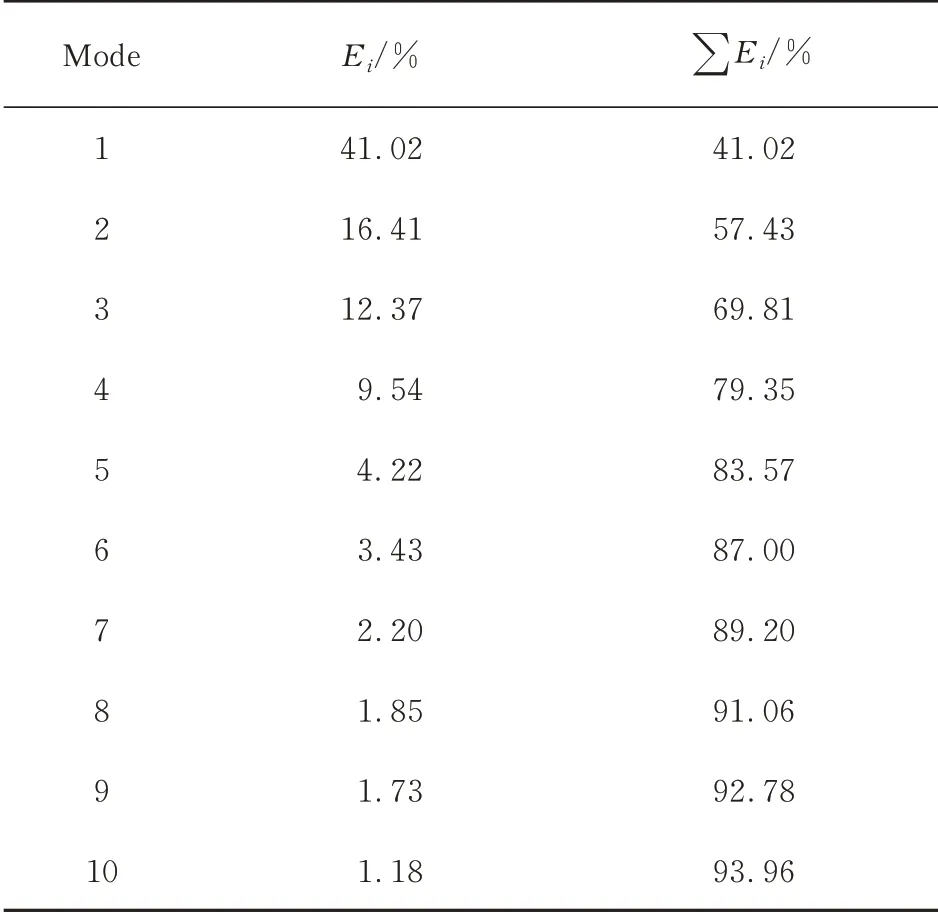
表2 各阶模态所占能量比例Table 2 The energy proportion of each mode
从表2及图6可以看出:从8阶开始,后续各阶模态能量占比均小于2%;前10阶模态占总模态能量的比例已经高达93.96%,因此由前10阶基模态重构得到的流场已经可以包含流场中的绝大多数信息。
限于篇幅,本文只给出第1、3、5、7阶POD基模态分布云图,如图7所示,可以看出:POD基模态涡核结构沿流向正负交替出现,前叶片叶背分离涡和尾缘脱落涡结构的波动均明显强于后叶片,占据流场中的绝大部分涡系能量,说明前叶片的流动不稳定性高于后叶片;此外,串列叶栅间隙射流在一定程度上阻碍了前叶片尾缘脱落涡与后叶片叶背分离涡之间的干涉作用,从而避免了后叶片叶背分离涡的增强,使得后叶片即使在较大的来流攻角下也能保持较好的流动状态;随着阶数增大,高阶模态云图中相邻涡核结构的距离缩小,表明高阶模态可能捕捉到了串列叶栅流场中更小尺度的涡系结构,涡核之间的相互作用与影响也更为复杂。
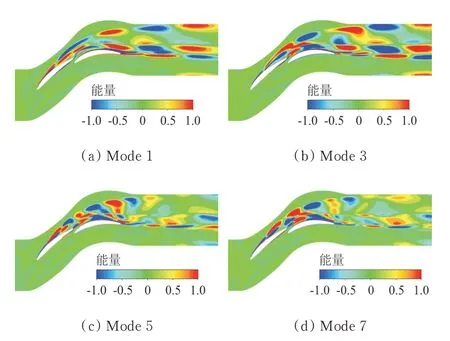
图7 各模态无量纲化能量分布Fig.7 Dimensionless energy distribution of each mode
t=1时间步原始流场涡量云图及使用低阶模态重构得到的涡量云图如图8所示,可以看出:使用前4阶POD基模态重构的流场已经可以反映原始流场的绝大多数流动结构,前8阶基模态重构流场与原始流场仅存在细微差别,随着模态阶数进一步增大,重构流场对原始流场细微结构的表达也更加清楚。这一结果与根据模态能量占比得出的结论一致。
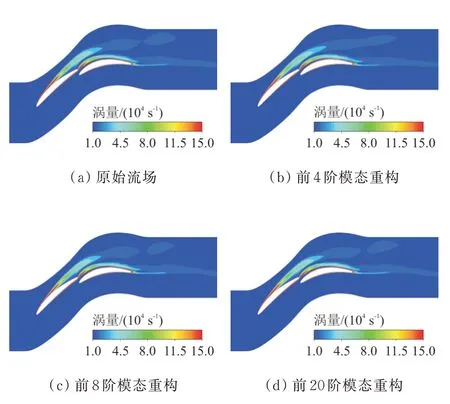
图8 原始流场及重构流场涡量分布图Fig.8 Original& reconstructed vorticity distribution
2.3 流场预测结果分析
从上述原始样本集(100个连续时间步流场)中随机抽取60个样本流场快照,用于获取POD基函数及相应的系数。而后将60个样本流场的时间步作为输入,将POD模态系数作为输出,构造RBF神经网络降阶模型,从而实现对非样本流场POD模态系数的预测。
使用POD-RBFN混合模型对非样本流场进行预测,定义流场整体重构误差为

式中:下标m为重构的目标流场时间步数;N为流场马赫数分布云图中的节点数;Ma为该时刻重构流场中第i个流场节点的当地马赫数值;Ma为该时刻原始流场第i个节点的当地马赫数值。
分别采用不同的模态阶数对某时刻流场(非样本流场)进行预测,得到整体重构误差随模态阶数的变化关系,如图9所示,可以看出:当模态阶数较少时,重构误差随模态阶数的增加急剧减小,但当模态阶数大于22后,重构误差随模态阶数增加而变化的幅值很小。这是由于前20阶基模态已经包含了流场98%以上的能量,更高阶的基模态所占据的流场能量份额极少,对流场重构的影响也很小。

图9 不同阶模态重构流场整体误差Fig.9 Overall reconstruction error with different modes
使用前10阶模态对某时刻流场(非样本流场)进行预测的结果如图10所示,重构流场的误差分布云图如图11所示,可以看出:使用前10阶模态预测的马赫数流场与原始流场仅存在细微差异;重构流场的误差主要分布在前、后叶片叶背分离涡及尾缘脱落涡涡核位置处,这是由于涡系结构的相互干涉、演变,使得该区域流动较为复杂多变,进而影响了流场的预测精度。

图10 原始流场及重构流场马赫数云图Fig.10 Mach number distribution of original and reconstructed flow field

图11 重构流场误差分布云图Fig.11 Reconstruction error distribution
2.4 自适应抽样结果分析
本文构造的POD-RBFN混合模型需要基于一定的样本数才能进行流场预测,而函数响应偏差的计算需要进行流场预测,故需要先从原始样本空间的100个流场快照中等距抽取11个样本作为自适应抽样的初始样本,然后采用基于函数响应偏差的自适应抽样方法进行抽样。抽样对象为一维时间步序列,故每次抽样后会得到两个新的样本点,总共进行20次自适应抽样。
分别使用自适应抽样和随机抽样得到的样本点对随机25个时间步的流场进行预测,并求取重构误差的均值,平均重构误差随样本数增加而变化的曲线如图12所示,可以看出:经过自适应抽样之后,相同样本数下的重构精度得以提高,达到同一精度所需样本数量明显降低,比如图中采用自适应抽样之后,只需要45个样本就能达到随机抽样60个样本的重构精度,样本数量减少了25%。
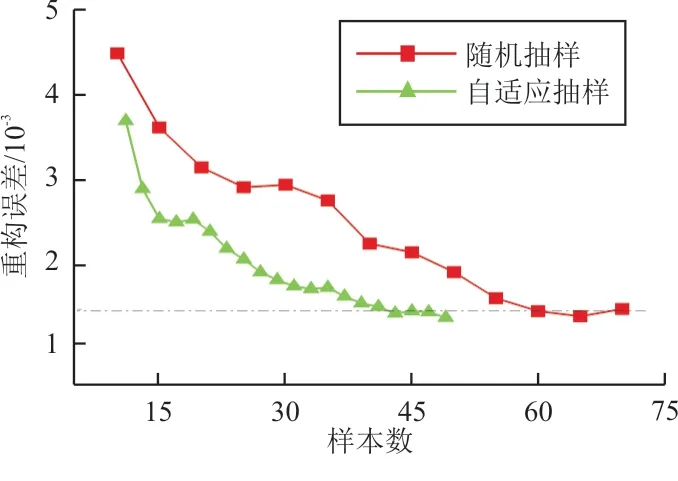
图12 重构误差与样本数的关系曲线Fig.12 Relation curve between reconstruction error and sample number
分别使用自适应抽样和随机抽样得到45个样本,对某时间步(非样本时间步)的流场马赫数分布进行预测,两种抽样方法进行重构的误差分布云图如图13所示,可以看出:自适应抽样方法明显降低了涡系结构发生、发展区域的流场重构误差,尤其是叶片下游尾迹处的流场重构误差,从而提高了流场的整体重构精度。

图13 两种抽样方法的重构误差分布云图Fig.13 Comparison of reconstruction error distribution
3 结论
(1)低阶POD模态包含了流场中的绝大部分能量;串列叶栅间隙射流的存在一定程度上阻碍了前叶片尾缘脱落涡与后叶片叶背分离涡之间的干涉作用,改善了后叶片的流动状态;高阶POD模态捕捉到了串列叶栅流场中更小尺度的复杂涡系结构。
(2)POD-RBFN混合模型能够有效捕捉流场的主要模态特征,并通过低阶重构的方式对非样本流场进行快速预测,预测误差主要分布在前、后叶片叶背分离涡及尾缘脱落涡涡核位置处。
(3)采用基于函数响应偏差的自适应抽样方法能够有效提高降阶模型的采样效率,与静态随机采样相比,达到同样重构精度所需的样本数降低了25%左右。
