基于多尺度1DCNN的滚动轴承故障诊断
2022-10-25杜文辽侯绪坤王宏超巩晓赟
杜文辽,侯绪坤,王宏超,巩晓赟
(郑州轻工业大学机电工程学院,河南郑州 450000)
0 前言
滚动轴承是旋转机械中重要的零部件之一,同时也是最易受损的零部件。据不完全统计,在旋转机械中,约有1/3的机械故障源于滚动轴承。为了避免轴承故障带来的经济损失和安全隐患,对滚动轴承进行监测、分析,并及时进行诊断故障就显得尤为重要。
目前轴承故障诊断过程主要包括3个方面:数据预处理、特征提取及模式识别。传统的故障诊断主要通过时域、频域以及时频域分析将信号映射到统计参数来获得特征,基于快速傅里叶变换的频域特征会丢失时域的变化信息,而基于时域方法的特征会丢失频域的变化特征。此外,信号被简单地用作故障诊断的单一维度向量,难以保证诊断精度。为了解决这一问题,主要通过局部特征尺度分解、经验模态分解(EMD)、小波变换(WT)等时频域分析方法提取故障多维特征并将其作为模式识别的依据。其中小波变换可以对非平稳、非线性的振动信号进行多尺度分解,从而准确提取时频域中所蕴含的不同尺度的故障特征信息,已被大量学者使用。WANG等使用离散小波变换和稀疏表示获得了新的稀疏小波能量特征来识别滚动轴承故障;SHEN等描述了一种基于小波变换、距离评估技术和支持向量回归的智能故障诊断方案,并将其用于轴承的故障模式分类。以上方法均取得一定的诊断效果,但这些基于信号处理的故障诊断方法仅针对特定问题,而且需要人工提取特征,存在依赖于经验、自适应能力和泛化能力差的问题。对于模式不明且多变、多故障信息耦合的“大数据”,用这些方法难以提取出能有效表征故障的特征信息。
近年来,机械的复杂度和集成化不断提高,依靠人工知识和经验的传统故障诊断方法已经不适用现代智能化诊断。同时,深度学习(Deep Learning,DL)在图像处理、计算机视觉、语言识别等领域应用十分广泛。深度学习模型可以直接从原始信号中提取抽象特征,而无需人工提取特征,深度学习凭借其强大的非线性建模以及特征表征能力,在诸多方面表现出极大的潜力,已有许多学者将深度学习应用到机械设备的故障诊断中。雷亚国等利用去噪自编码器准确诊断了多级齿轮传动系统故障。DUONG、KIM构建了一种基于堆叠降噪自动编码器(Stacked Denoising Auto Encoder,SDAE)非互斥分类器(Non Mutually Exclusive Classifier,NMEC)方法的DNN(Dynamic Neural Network)结构,用于组合模式以实现轴承故障诊断;LI等利用深度信念网络直接从轴承原始信号中取得故障特征并对其进行了准确诊断。虽然这些方法均能从机械“大数据”中自动提取出机械设备不同故障特征,但都是针对单一的时域或频域信号进行特征学习,难以提取到更具表征性的时频域特征信息。为了避免仅学习单一维度的特征而影响诊断精度,故有必要利用小波变换对原始信号进行多尺度分解,对得到的信号的各尺度成分进行重构,构建利于特征学习的频谱表示,以从中学习到更为有用的故障特征信息。
深度卷积神经网络(Convolutional Neural Networks,CNN)是一种典型的深度学习模型,最早由LECUN提出,目的是处理己知网格状形状的数据,如二维图像数据或一维时间序列数据。CNN通过卷积、池化和非线性激活函数映射逐层提取信号的特征。与其他深度学习模型相比,CNN具有更强的鲁棒性和更好的泛化能力。同时,CNN通过权重共享和池化操作提高了网络性能并降低了训练成本,并且与其他深度学习模型相比不容易出现过拟合问题。目前,CNN已经应用在故障诊断中,主要包括一维卷积神经网络和二维卷积神经网络。在轴承的故障诊断中,由于输入信号是一维的,经典的二维CNN模型需要先将一维信号转换为二维图像,在一维信号下可能会失去优势,因此针对轴承的一维振动信号采用一维卷积神经网络模型进行诊断。
针对滚动轴承振动信号的非平稳、非线性的特征,利用小波变换对其进行多尺度分析,从而准确提取时频域中所蕴含的不同故障状态特征信息,然后将其代入构建的一维卷积神经网络模型进行特征学习和分类,实现故障的智能诊断。
1 理论基础
1.1 小波变换
小波变换是一种数据分析方法,可以对原始信号局部分析,其窗口大小可以随频率变化而变化,达到在时频域自适应分析信号的目的。
在平方可积实数空间()中,如果函数()满足容许条件:
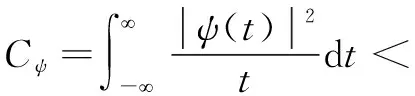
(1)
则()可选作基本小波。()通过伸缩和平移产生一个函数族{,()},称为小波函数。
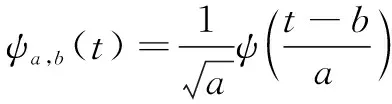
(2)
其中:是尺度因子;是位移因子。信号()的小波变换定义为

(3)
其中:()是小波函数()的共轭。
当机器发生故障时,采集到的振动信号波形复杂且不稳定,小波变换能够把任何信号映射到由一个母小波伸缩(变换频率)、平移(刻划时间)组成的一组基函数上去,实现信号在不同频带的自适应分解。
1.2 一维卷积神经网络
图1所示为一维卷积神经网络结构,它由输入层、卷积层、批量归一化(Batch Normalization,BN)层、池化层、全连接层、Dropout层以及输出层组成。
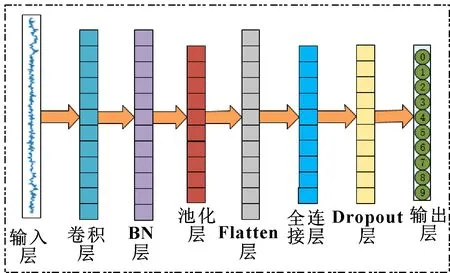
图1 一维卷积神经网络结构
1.2.1 输入层
输入层作为一维卷积神经网络的第一层,用来接收训练和预测的样本。
1.2.2 卷积层
卷积层可以有效地进行图像特征提取,卷积运算本身就是滑动卷积核与Feature Map 进行卷积运算。一维卷积运算是指使用一维卷积核对输入的一维信号进行局部卷积计算,生成一维卷积特征图。
1.2.3 批量归一化层
批量归一化(BN)是指对每一批数据做均值和方差归一化。它可以解决在训练过程中,中间层数据分布发生改变的问题,防止梯度消失或爆炸、加快训练速度。
1.2.4 池化层
经过卷积层之后,参数往往会较多,因此需要降采样操作,即池化操作,以减少神经网络的参数;同时池化层还具有特征不变性的特性,即减少数据的同时还能够保留原始数据的特征。常用的池化过程有均值池化(Average Pooling)和最大值池化(Max Pooling)。如图2所示,A为均值池化过程,B为最大池化过程。
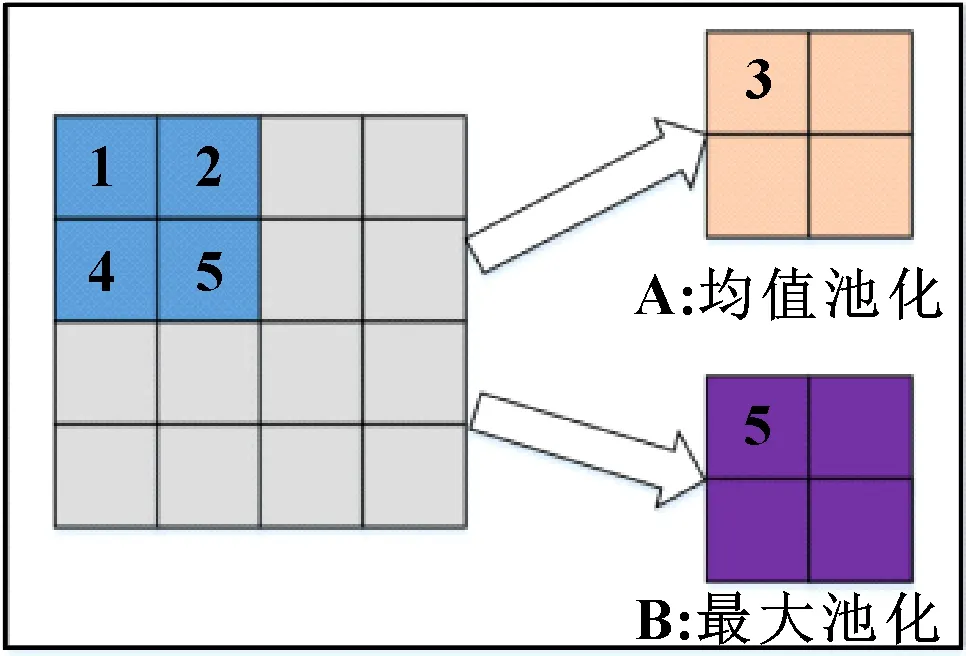
图2 池化过程
1.2.5 全连接层
经过池化层之后,需要将数据展平为特征向量,将这些向量输入到全连接(Fully Connected,FC)层中。全连接层是指该层的每一节点都与其上层的所有神经元结点进行连接,其下层可以为Dropout层或者输出层,如图3所示。全连接层通常位于网络的最后几层,其作用是整合上层网络中区分度较高的类别信息。该层中常用的激活函数为ReLU函数。
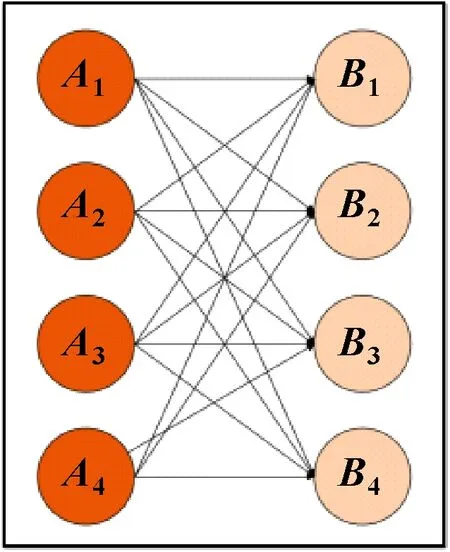
图3 全连接过程
1.2.6 Dropout层
Dropout层通常需要加在全连接层之后,其作用是防止过拟合现象的发生,减少网络中的参数,提高网络的泛化能力和鲁棒性。Dropout层分为前向传播和反向传播。前向传播是指给定每个神经元一个随机值(0~1之间),设定采样阈值,若该神经元对应的随机值小于采样阈值,则将该神经元设置为0,反之将该神经元设置为,并保留每个神经元对应的所有随机值和设置值。反向传播是指读取前向传播中的随机值,对数据进行和前向传播相同的操作,通常将采样阈值设置为0.5。
1.2.7 输出层
输出层主要实现了分类。隐含层经过训练后,最终通过输出层中Softmax分类器进行分类。
1.3 1DCNN的训练过程
一维卷积神经网络训练过程中更新权值可以分为两个部分:前向传播为神经网络根据样本计算预测值;反向传播则通过预测值与真实值之间的差异,采用梯度下降法进行权值更新。
(1)前向传播计算过程
一维卷积过程可用式(4)表示:

(4)
其中:表示卷积核;表示卷积核的个数;为卷积计算区域;表示第个数据;-1为第层卷积输入;为卷积输出;Conv1D()为一维卷积计算;为偏置;()为激活函数。激活函数为ReLU函数,表示为
()=max{0,}
(5)
其中:为卷积层激活值。
(2)误差反向传播过程
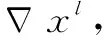
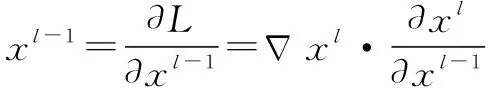
(6)
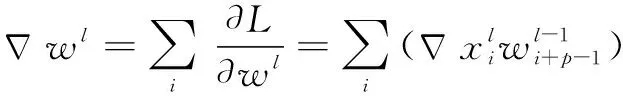
(7)
其中:为目标函数;-1为上一层原始值;为需要更新的参数。
2 WT-1DCNN诊断模型及流程
基于小波变换和一维卷积神经网络的诊断模型进行滚动轴承故障智能诊断可以分为以下8个步骤,如图4所示。
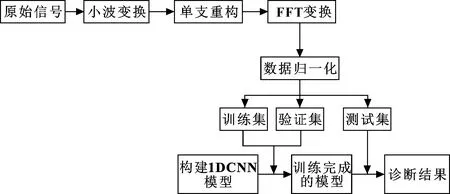
图4 故障诊断流程
(1)通过传感器采集滚动轴承工作状态的振动信号;
(2)对信号进行小波变换,得到信号的多尺度表示;
(3)对每层小波信号进行单支重构;
(4)对重构的信号进行快速傅里叶变换,得到信号的幅值谱;
(5)将得到的幅值数据进行归一化处理,并将各尺度数据构造成一维特征向量作为特征样本;
(6)将得到的特征样本按照一定的比例分配为测试样本、验证样本及训练样本;
(7)构建一维卷积神经网络。利用训练样本对1DCNN进行训练,并用验证样本验证,最后得到诊断模型;
(8)将测试样本输入网络进行验证,得到最终的诊断精度。
3 实验验证及分析
3.1 数据描述
实验数据来自于凯斯西储大学滚动轴承数据集。加速度传感器安装在电机驱动端的轴承座来获得轴承的振动信号,采样频率为12 kHz。电机驱动端轴承型号是6205-2RS JEM SKF深沟球轴承,其故障通过电火花加工。故障直径共有3种,分别为:0.18、0.36、0.53 mm,故障深度均为0.28 mm。轴承在转频为大约为30 Hz、4种载荷(0,735 W,1 470 W,2 205 W)下实验,分为4种状态:正常状态(N),外圈故障(OF),内圈故障(IF),球故障(BF);每种故障状态有3个故障程度:轻微故障(0.18 mm),中度故障(0.36 mm),严重故障(0.53 mm)。将数据集共分为10种健康状态,每种健康状态共有400个数据样本,共计4 000个数据样本,随机抽取70%数据样本作为训练样本,剩余30%作为测试样本,将训练样本的30%作为验证集,如表1所示。
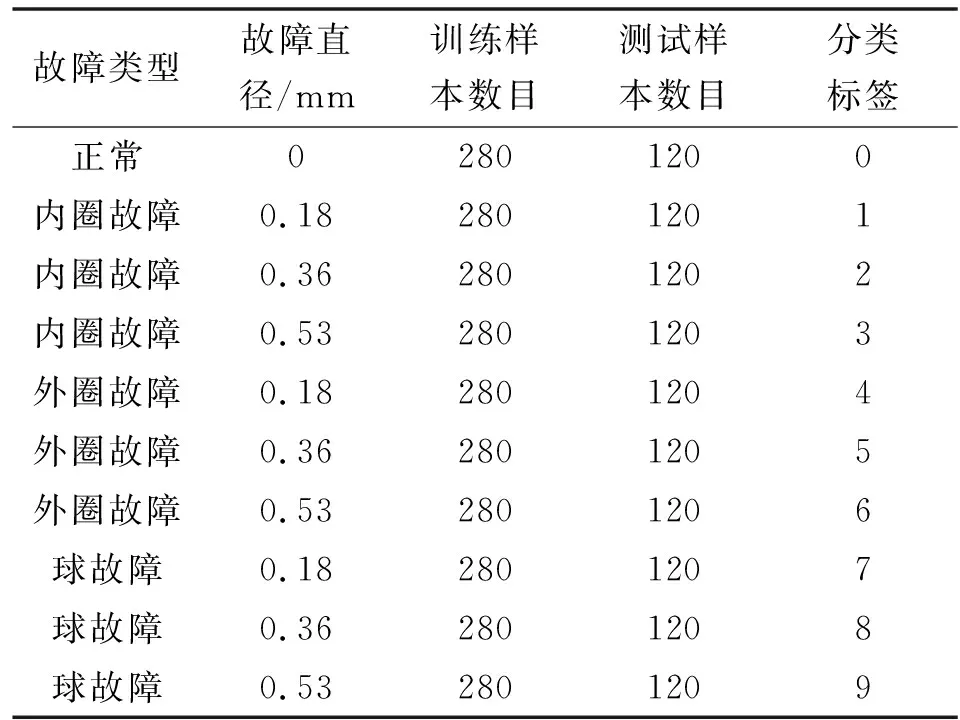
表1 实验数据样本
3.2 模型构建
对上述滚动轴承数据样本采用db5小波进行3层分解,然后将每层的小波系数进行单支重构;对重构后的信号进行快速傅里叶变换,得到FFT频谱表示;将得到的频谱数据做归一化处理,作为1DCNN模型的输入,其中激活函数选用ReLu函数。
此次实验使用的编程语言为Python3.6,解释器为PyCharm,神经网络框架为Keras。在构造1DCNN模型时,共设置有11层网络,包括输入层、3个卷积层、3个BN层、池化层、Dropout层、全连接层、输出层,如表2所示。
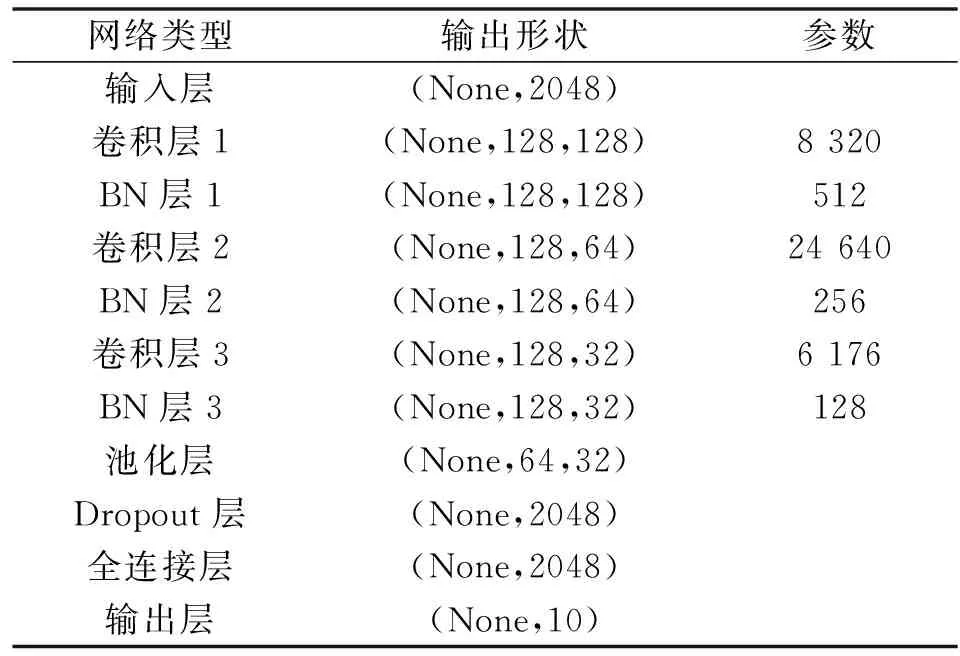
表2 一维卷积神经网络结构
3.3 结果分析
图5所示为训练集和验证集的正确率和损失随着训练次数递增的变化情况,可以看出:当训练次数达到5次时,网络已经趋于稳定,训练集和验证集的正确率已经达到100%,可以看出此次1DCNN模型具有良好的效率。

图5 损失率(a)和正确率(b)随着训练次数的变化
取10次实验过程中准确率最高的一次,将其分类结果用混淆矩阵表示出来,如图6所示。可以看出:此次实验共有10种故障类型,每种故障类型都有120个样本,每种故障类型都能准确地分类出来,准确率高达100%。
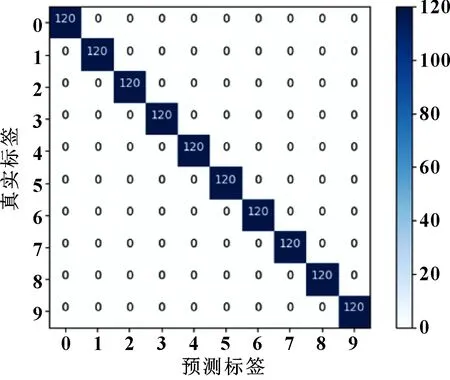
图6 训练样本混淆矩阵
将最后一层分类结果用分布随机邻居嵌入(-SNE)可视化表示,经过WT-1DCNN模型进行处理之后,可以将每种的故障类型正确分类,10种颜色分别代表10种故障类型,每种故障类型都能够聚集在一个区域内。
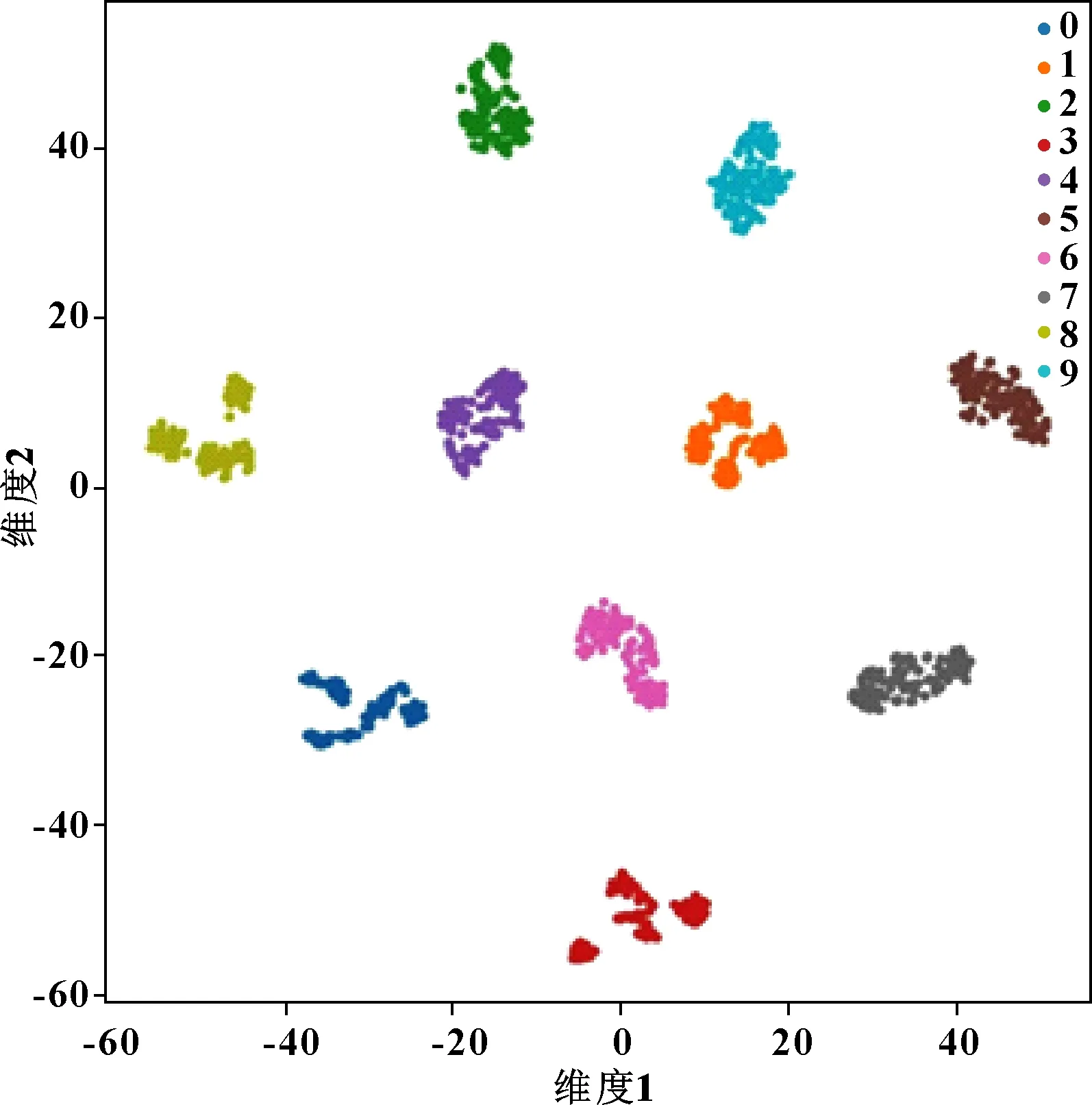
图7 分类结果的t-SNE可视化
针对测试样本,为了避免一次实验数据带来的误差,共进行10次实验,每次实验正确率如图8所示。经计算得到10次实验的平均正确率为99.94%。从图8中可以看出测试集准确率在99.74%~100%内,说明此次实验选取的模型具有良好的稳定性。
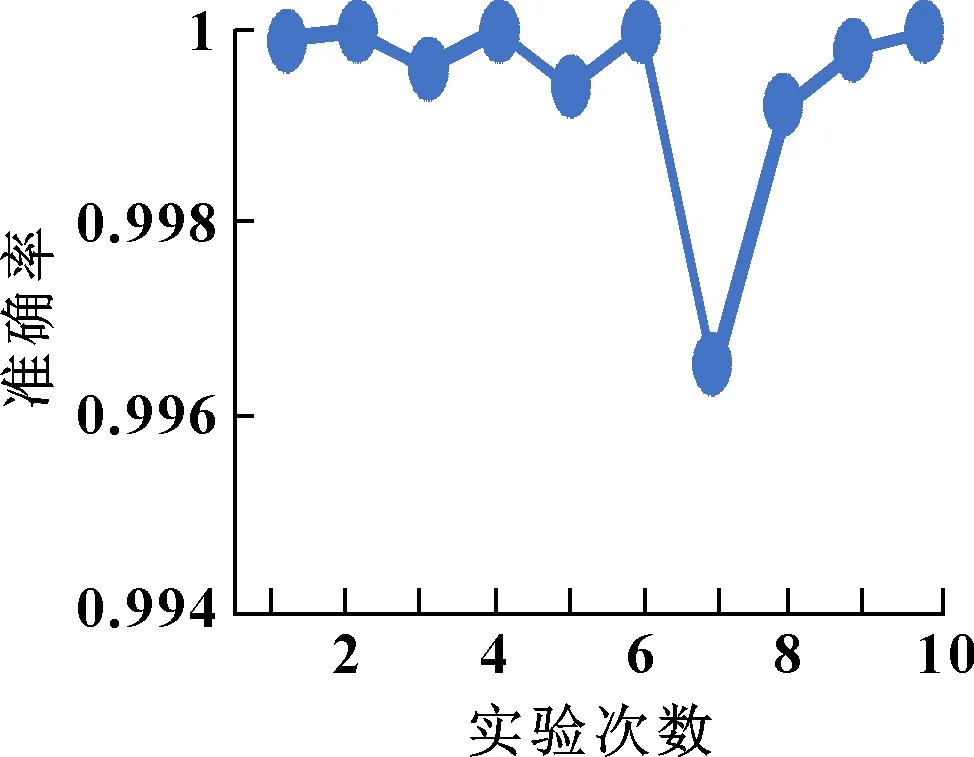
图8 WT-1DCNN模型10次实验准确率
3.4 讨论比较
为了说明小波变换能够针对非平稳振动信号准确提取故障特征,将原始信号直接输入1DCNN进行特征分类与经过小波变换后的特征样本输入相同的1DCNN模型进行特征分类并将两种方法的故障诊断准确率进行对比。同样进行10次实验,计算出直接输入1DCNN模型轴承故障诊断准确率的平均值为98.02%,而经过小波变换后输入WT-1DCNN模型的平均诊断精准确率为99.94%,结果如图9所示。可以看出:10次实验过程中每次实验1DCNN模型的诊断精度都明显低于WT-1DCNN模型的精度,证明小波变换可以准确提取信号多尺度特征,提高轴承故障诊断的精度。
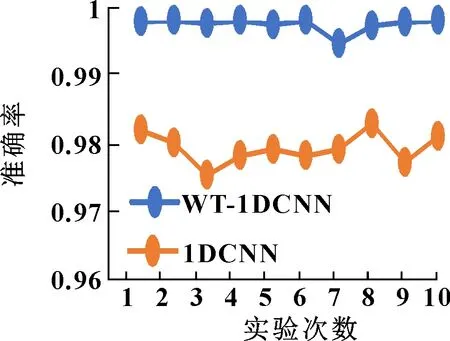
图9 1DCNN与WT-1DCNN准确率对比
为了验证文中所提方法的优越性,针对相同的数据集,分别与不同的方法进行对比。DU等提出了一种基于小波领导多重分形特征的滚动轴承故障诊断方法(Wavelet Leaders),得到88.9%的正确率;李恒等人提出了基于短时傅里叶变换和卷积神经网络的故障诊断方法(STFE-CNN),实现了端到端的故障模式识别,诊断正确率为97.93%。XIA等提出了基于CNN的多传感器融合方法(MCNN),将多个传感器的信号进行融合再输入到CNN中,对轴承10种故障状态进行诊断,得到99.41%的正确率;DING、HE提出一种基于小波包能量(WPE)图像和二维深度卷积网络的新型能量波动多尺度特征挖掘方法(WPE-2DCNN),用于轴承故障诊断,正确率达到了98.8%。 将5种方法进行比较,结果如图10所示,可以看出文中所用WT-1DCNN方法的故障诊断准确率最高。
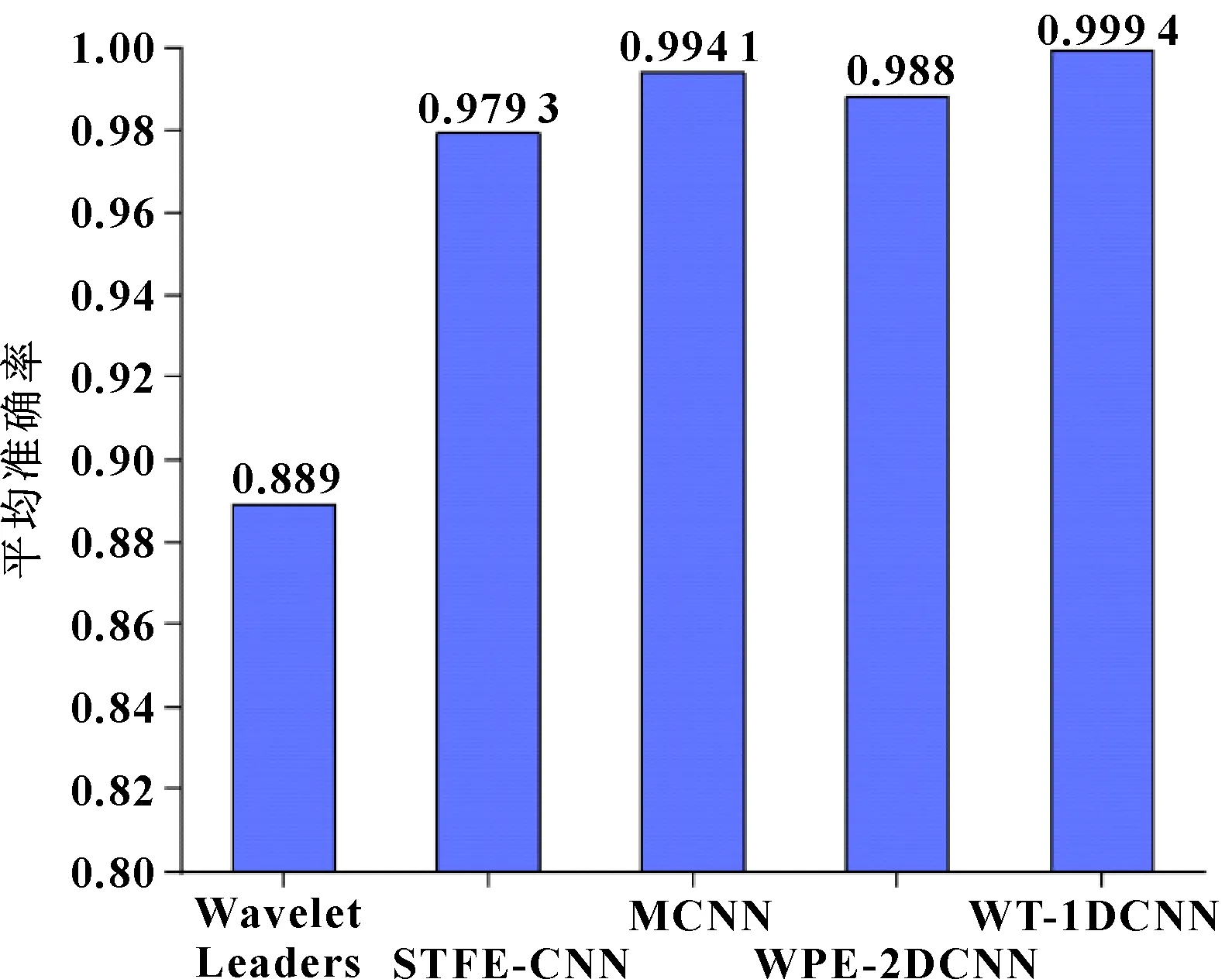
图10 不同方法诊断准确率
4 结论
为了解决轴承故障诊断中人工特征提取依赖经验和准确提取一维信号中蕴含故障特征难度大的问题,提出一种多尺度一维卷积神经网络模型对轴承进行故障诊断。与其他诊断方法相比,该方法有如下优点:
与传统的智能诊断方法相比,利用小波变换对信号进行多尺度分析,可以更有效地挖掘故障数据中隐藏的特征分布,准确地提取信号中蕴含的轴承故障特征,提高故障诊断的精度。
采用一维卷积神经网络对输入的一维信号进行训练,无需将一维信号转换为二维图像,有效地融合了特征自动学习和故障分类,避免了人工提取特征,简化了轴承诊断过程,获得了优于其他方法的诊断效果。
