二轮平衡车的神经元控制算法及仿真

沈浩宇，江先志，冯涛

(1.浙江理工大学机械与自动控制学院，浙江杭州 310000；2.深圳海关工业品检测技术中心，广东深圳 518000)

0 前言

二轮平衡车是一种特殊的轮式机器人，它是一个融合了动力学、自动控制理论、电子技术、电机技术的综合性研究课题。它利用车体内部的陀螺仪和加速度传感器检测车体姿态的变化，并利用伺服控制系统精确地驱动电机进行相应的调整，以保持系统平衡。二轮平衡车本质上是一个可移动的倒立摆系统，具有多变量、强耦合性、非线性、动态不稳定的特点。

目前二轮平衡车采用的控制算法有PID控制、模糊控制、滑模控制、预测控制、H控制、LQR控制等。文中采用神经元PID控制算法控制二轮平衡车，以测试神经元PID控制的效果。PID控制是迄今为止在过程控制中应用最广泛的控制方法。但是在实际应用中，经典PID控制器的控制参数为人工整定后固定不变，要想将其调节到较为理想的状态，整定过程费时费力。实际被控对象往往具有非线性、时变不确定性，难以建立精确的数学模型，常规的PID控制器不能达到理想的控制效果。

近年来，神经网络算法迅速发展，引起了人们越来越多的兴趣和普遍重视。由于BP神经网络能够通过神经元反馈进行学习，不断调整各层神经元之间的连接权重，适应被控系统的不确定性和非线性 ，由神经元构成的控制器具有更好的灵活性和适应性。

1 二轮自平衡车分析

二轮平衡车三维模型如图1(a)所示，二轮平衡车简图如图1(b)所示。在图1(b)中，跟随车身的动坐标系原点建立在车轴的中心处，轴正方向为二轮平衡车的前进方向，轴与重力方向的反方向重合，轮子绕轴转动。为二轮平衡车绕轴旋转的角度，为二轮平衡车的倾角，和分别为二轮平衡车左轮和右轮的输入转矩。

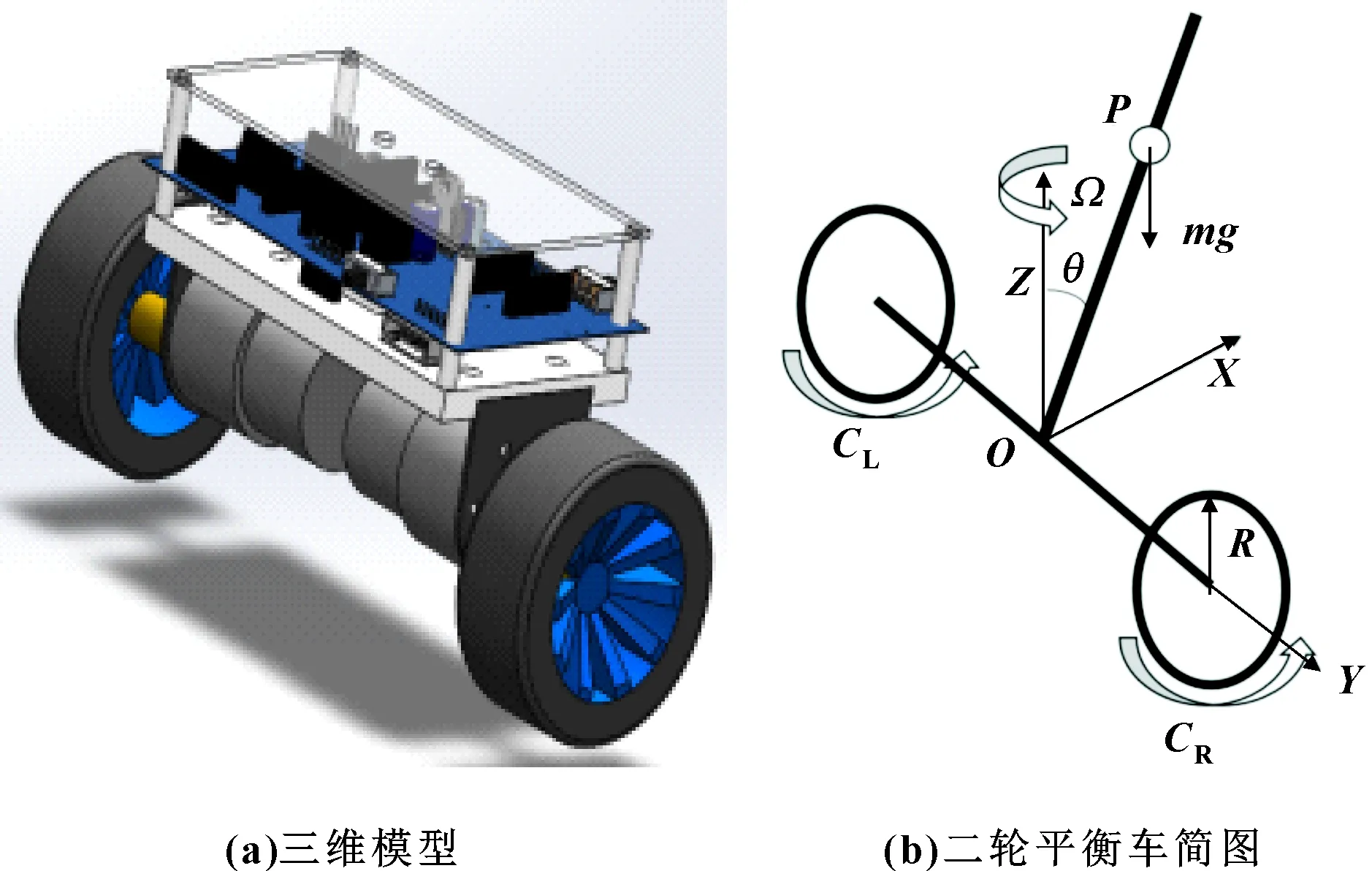
图1 二轮平衡车三维模型及简图

二轮平衡车的重心位于车轮轮轴上方的点，由于点位于车体上部，在无外力的作用下，车体将会发生倾倒，故二轮平衡车属于动态不稳定系统。二轮平衡车的车轮采用共轴对置放置的方式，并且两轮由2个电机相互独立驱动。二轮平衡车通过调整前后运动的加速度来保持自身平衡，还具备通过控制左右车轮转速差实现转向的功能。

2 二轮平衡车控制系统设计

二轮平衡车需要被控制的变量有车体运行速度、倾斜角度和偏航角度，而控制输入量只有作用于左右两轮的电机输出扭矩，所以二轮平衡车是一个典型的欠驱动系统。各个被控变量和控制输入量之间的关系是非线性的，各个被控变量之间具有强耦合性。针对二轮平衡车欠驱动、多变量、强耦合、非线性等特性，采用神经元PID控制器进行控制。神经元PID控制器是一种自适应智能控制器，能够针对不同的工况自动整定PID参数，具有自学习自适应能力，使被控对象达到良好的控制效果。

2.1 神经元PID控制器

在神经网络理论中，神经元模型可模拟生物神经元的3种基本功能。首先，根据不同的权重对所有输入信号进行不同程度的加权，然后将这些信号相加以获得组合效果。最后，利用神经元输出函数进行信息输出。神经元PID控制器是采用人工神经元建立的PID控制器模型，通过BP神经网络算法调整PID参数。神经元网络计算量小、运行速度快，且可自适应调整权值。将它用在PID闭环控制中，形成单神经元PID控制器。这样PID参数整定过程就相当于单神经元网络的权值调整过程。人工神经元PID控制器的结构如图2所示，单神经元控制原理如下：

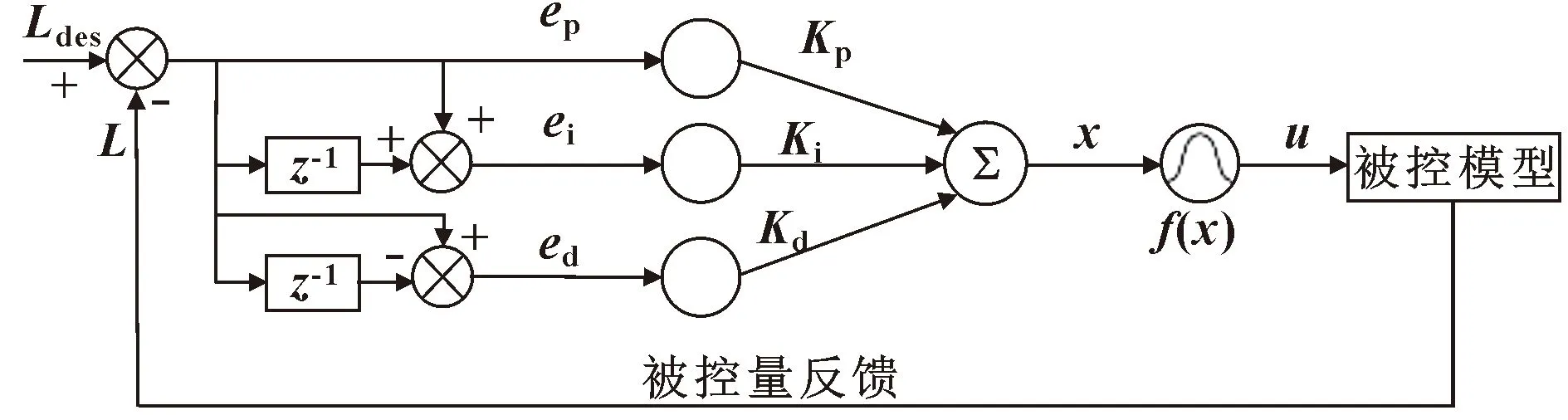
图2 神经元PID控制算法原理

由图2得到神经元PID控制器的前向传播过程：

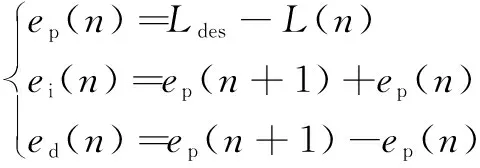
(1)

=++

(2)

采用Sigmoid型函数，对进行限幅输出，使得输出值限制在合理的范围：

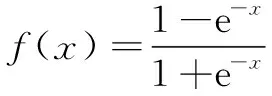
(3)

=()

(4)

误差指标为

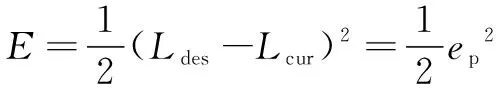
(5)

BP算法采用的误差反向传播是按照误差指标函数()的负梯度方向不断修正权值以达到神经元的输出逼近期望的目的。根据前向传播过程，得：

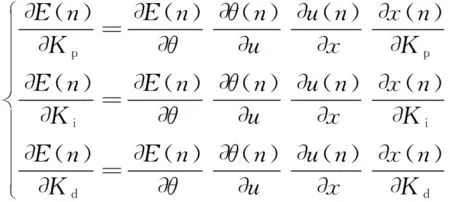
(6)

控制器的目标是让实际当前值与目标值的误差指标最小。根据BP算法进行PID参数的更新，PID参数的迭代使得系统的误差指标尽可能小。迭代公式为(7)，其中、、分别为比例增益、积分增益和微分增益的学习步长。

(7)

由式(5)得神经元控制指标对被控制量的偏导为

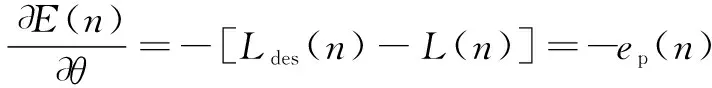
(8)

由式(3)得到限幅函数()对神经元输出量的偏导为

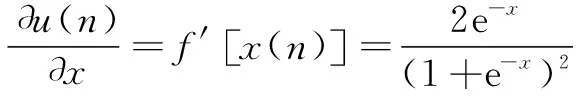
(9)

被控系统对控制信号的偏导可以设为

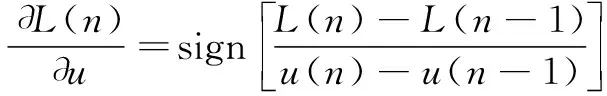
(10)

由式(2)得神经元输出量对比例增益、积分增益、微分增益的偏导为

(11)

将式(8)—(11)代入式(6)，再根据式(7)得神经元PID控制器的比例增益、积分增益和微分增益的迭代更新算法：

(12)

2.2 神经元PD平衡控制器

二轮平衡车的平衡是通过前后移动保持的。将平衡车偏离平衡位置的角度作为偏差，通过负反馈控制消除偏差。

在仅有比例控制的情况下，二轮平衡车处于平衡位置时，因为偏差为0，所以控制器输出也为0。但是，车体绕车轴转动时具有惯性，平衡车会往另一个方向倒去，如此反复，平衡车会在平衡位置出现振荡且无法停止。由于平衡车绕轮轴的转动惯量客观存在，控制平衡车平衡不仅需要施加和倾角成正比的回复力，还需要和角速度方向相反的阻尼力进行叠加，才能达到控制平衡的效果。

平衡车的平衡控制需要快速性，故比例系数较大。当比例系数较大时，系统几乎不存在静差。因为PID控制器中积分的作用是消除静差，所以静差对于直立控制的影响很小，自然就不需要积分。实际上，平衡车并不一定要完全处于机械中值，略微的偏移不会有太大影响。因此，对于准确性要求不高的系统可以不引入积分控制，平衡车只需PD控制即可实现直立。因此，将平衡控制器设计为PD平衡控制器。

构建PD平衡控制器，如图3所示。

图3 PD平衡控制器

为实现PD参数可调，引入神经元PD平衡控制器，如图4所示。

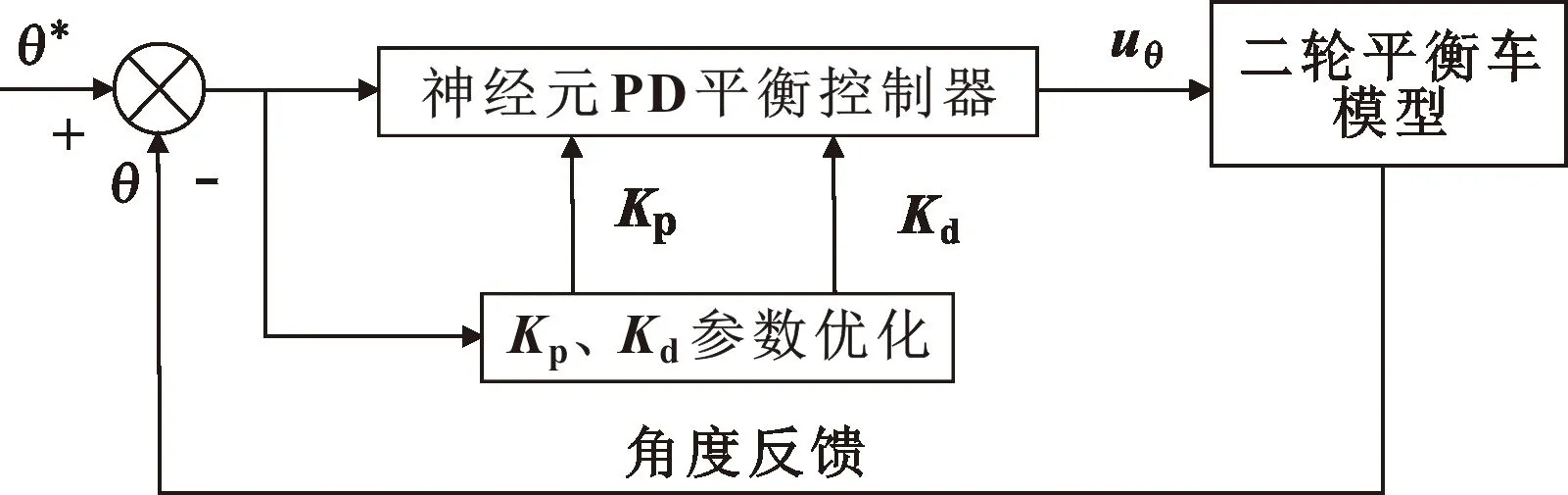
图4 神经元PD平衡控制器

根据式(4)，神经元PD平衡控制器的前向传播过程如下：

=(pp+dd)

(13)

由式(5)，设置平衡控制器的误差函数为

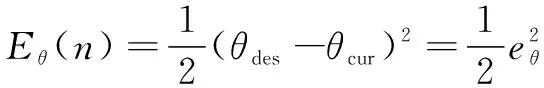
(14)

其中：代表目标值；()代表传感器的检测值。

由式(6)—(11)可知神经元PD平衡控制器的PD参数的更新过程如下：

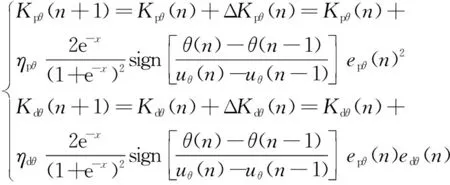
(15)

2.3 神经元PI速度控制器

因为平衡车的速度控制是在平衡车进行直立控制的前提下进行的，所以速度控制相比直立控制更加复杂。为保证直立控制的优先级，把速度控制器放在直立控制器的前面，即速度控制调节的结果仅仅是改变平衡控制的目标值。平衡车运行的加速度与平衡车倾角相关。若要提高平衡车向前行驶的速度，就需要平衡车向前倾斜，车轮在直立控制的作用下向前运动保持平衡车平衡。反之亦然，因此速度控制可以通过调节平衡控制的目标值来实现。根据上述过程，将速度控制器与直立控制器进行串联。将速度控制器的输出作为直立控制的输入，将直立控制的输出作为系统输出。设计出串联的平衡车控制器，如图5所示，这其实就是一个串级速度控制系统。

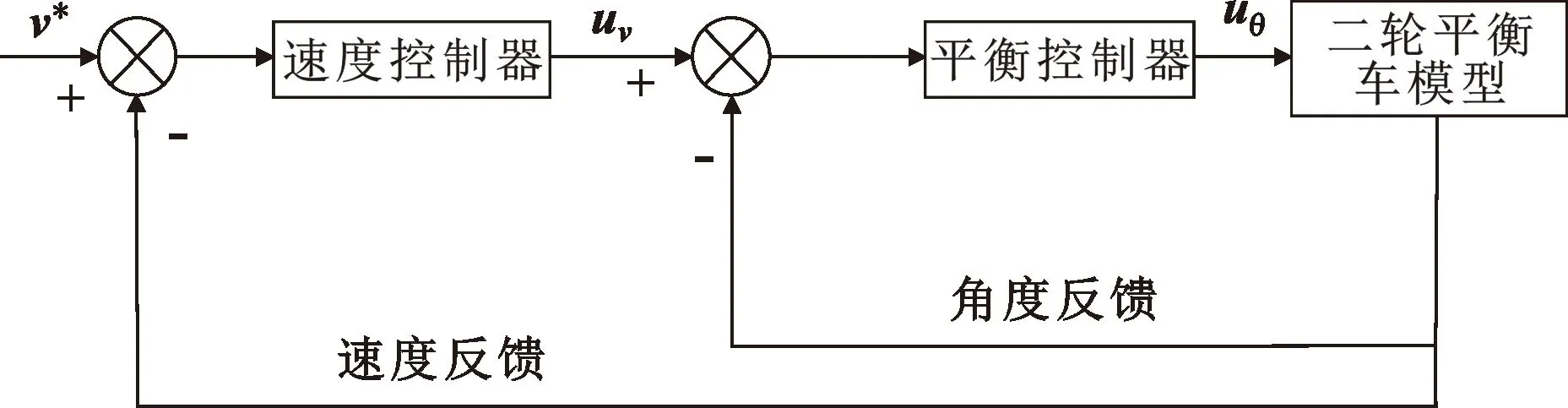
图5 串级PI速度控制

测量的机械中值与实际值存在误差，若只有平衡控制器，平衡车会一直前进或后退来维持有误差的测量中值，此时，速度控制器的输出将修正平衡控制器的目标值。当平衡车一直前进或后退，速度与目标速度之间存在静差。PI控制器具有消除静差的特点，使得平衡车可以稳定在原点，故速度控制器选用PI控制器。

为了实现速度控制器的PI参数可调节，速度控制器采用神经元PI控制器，如图6所示。

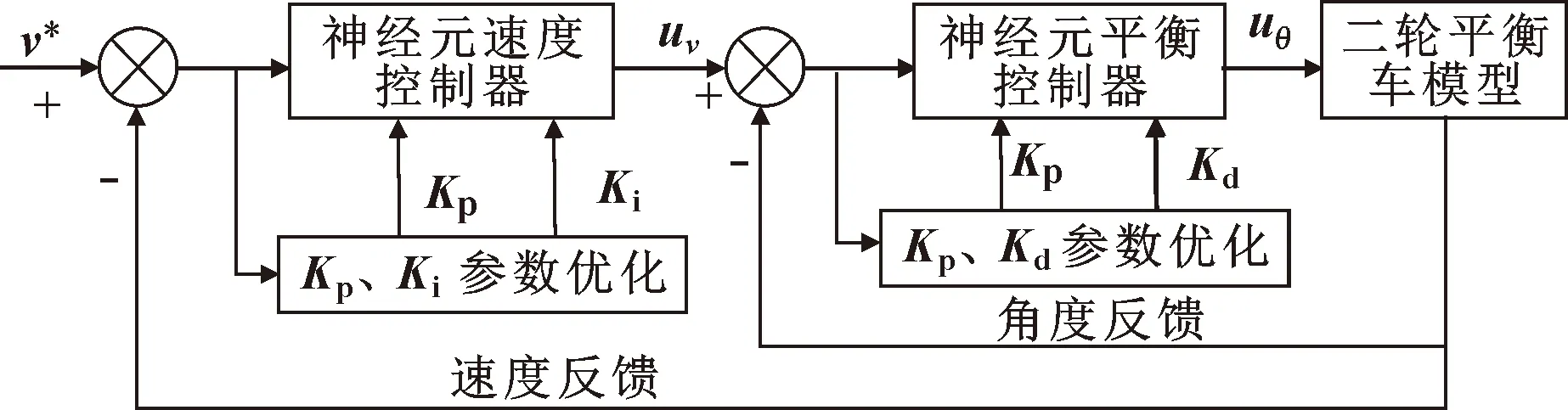
图6 串级神经元PI速度控制

神经元平衡控制器的前向传播算法公式：

=p(p-)+dd

(16)

=(pp+ii)

(17)

将式(17)代入式(16)得到：

=p[p-(pp+ii)]+dd

(18)

由式(5)，设置神经元速度控制器的误差函数为

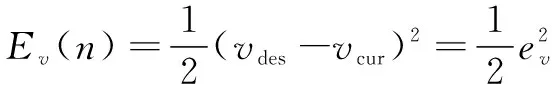
(19)

由式(6)—(11)可知PI参数的更新过程如下

(20)

2.4 PD转向控制器

由于平衡车对转向控制的响应要求不高，故转向控制器为简单的PD控制器。若设轴目标角度为0，则平衡车沿一条直线行走。

根据式(1)得到转向控制器的算法：

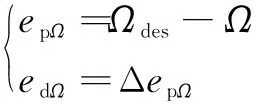
(21)

=pp+dd

(22)

二轮平衡车由左右轮的差速来控制方向，故将转向控制器的输出值作为速度控制器输出值的调整值，分别输出给左右轮的电机驱动

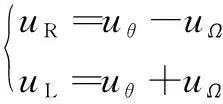
(23)

将转向控制器与串级速度控制器串联，构建了二轮平衡车的神经元PID控制系统，如图7所示。

图7 二轮平衡车神经元PID控制系统

3 搭建二轮平衡车仿真环境

在Simulink环境中通过组装Simscape提供的基本部件或运用基于Simscape基本组件创建新组件，可以快速创建电机、桥梁、整流器、液压执行器和制冷器等物理系统。Simscape的基本组件可以使用MATLAB变量和表达式参数化模型。Simscape可帮助开发控制系统并测试控制系统的性能。

如图8所示，Simscape中的Multibody主要包含带和缆绳、形状元素、约束限制、曲线和曲面、力和扭矩、坐标转换、齿轮和配合、运动关节、机械配置九大基本组件集合。Multibody为机器人、车辆悬架、建筑设备和飞机起落架等3D机械系统提供仿真基本组件，可以表示身体、关节、约束、力和传感器的基本组件，以对系统进行建模。Simscape可以将完整的CAD组件(包括质量、惯性、接头、约束和3D几何形状)导入模型，为整个机械系统制定和解决运动方程，仿真运行时自动生成3D动画来实现系统动态可视化。

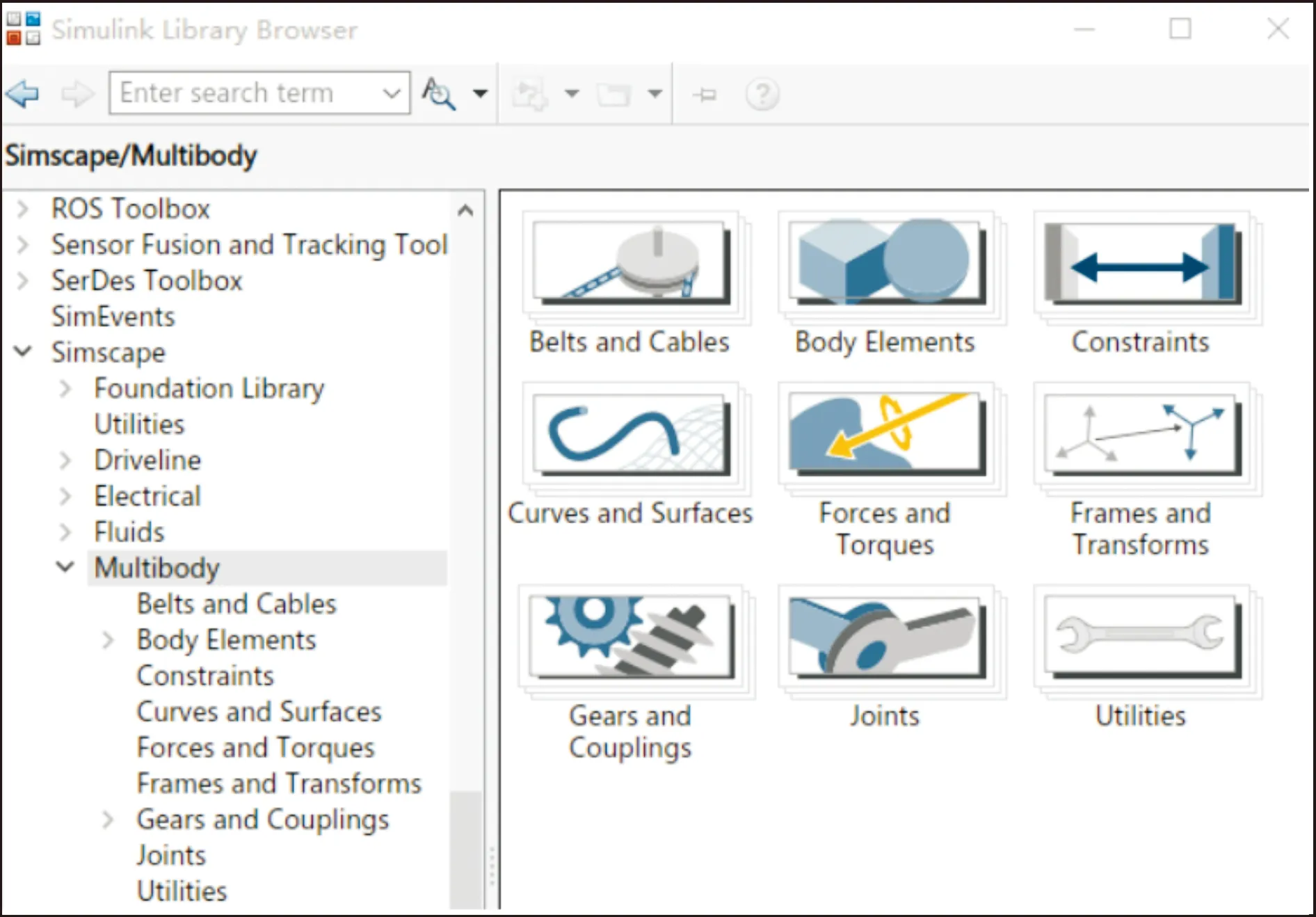
图8 Multibody集合

3.1 搭建二轮平衡车仿真模型

根据实物在SolidWorks中构建出车体零件，并进行装配。将构建的各个零件转换为STEP格式，导入形状元素组件集的文件实体组件中。二轮平衡车主要包含的零部件如表2所示。编写M文件，将零部件的颜色、质量等参数合存储为工作区变量，可以在仿真的实体组件中引用变量作为零件的属性参数。

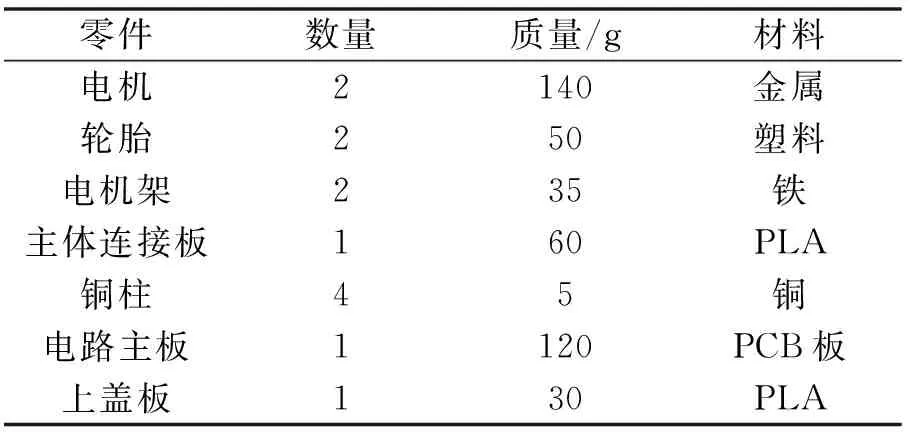
表2 DWC机器人零件

如图9所示，设置重力环境、世界坐标系、仿真求解器组件，三者缺一不可。世界坐标系原点为车轴的中心，通过设置坐标变换组件将地面放置在合适的位置，地面与车轮之间连接有接触应力组件；通过滑动关节组件与平面关节组件连接，首先保证左右车轮具有固定的相对位置，其次平面关节保证车轮具有前后、左右2个自由度，滑动关节保证二轮平衡车沿受重力落在地面上，在车轮与地面之间接触形成压力。如图10所示，以右轮为例，将转动关节组件安置在合适的位置，将车轮进行坐标转换与转动关节组件连接。转动关节组件接收转矩的输入与转动关节的角速度输出，并保证轮子的旋转自由度；如图11所示，车轮轴线与车体之间由转动关节组件连接，该转动关节接收扭矩的输入和角度输出。车体分为左右电机、电机架、电路主板、主体连接板、上盖板、铜柱等。

图9 二轮平衡车系统

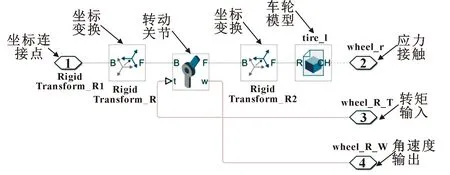
图10 右轮模型

图11 倾角关节

3.2 搭建控制系统

运用Simulink搭建仿真控制系统，如图12所示，图右边部分为二轮平衡车的控制系统。根据图5所示的控制系统结构，搭建仿真模型，通过左边的仿真模型采集模型的倾角信息、转向角信息、轮速信息并进行单位转换。

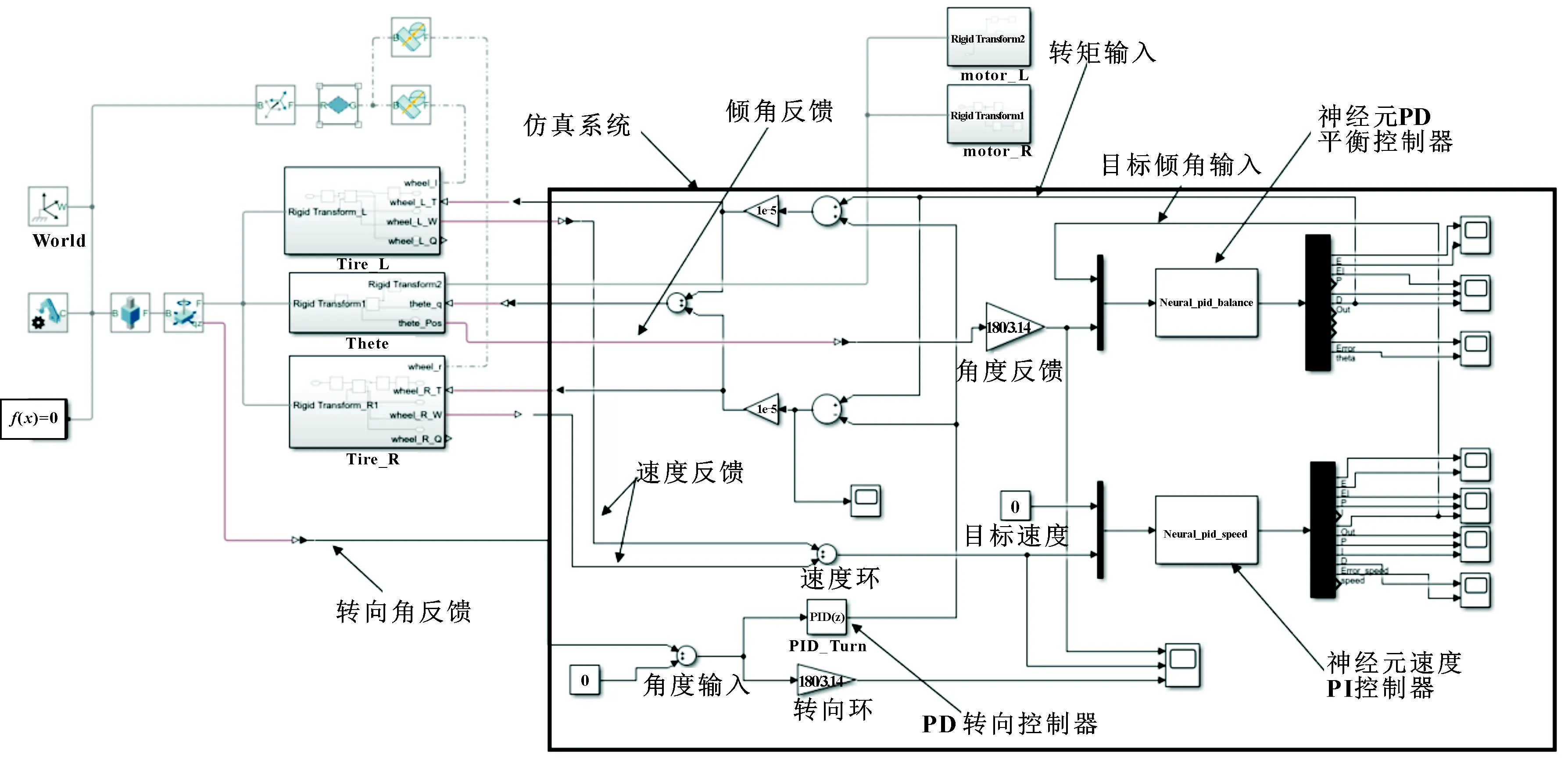
图12 Simulink仿真系统

S-Function全称System-Function，S-Function能够与Sinulink引擎交互，它极大地拓展了Simulink的功能。S-Function可以容纳连续、离散和混合系统，在S-Function中编写算法，并添加到Simulink模型中。S-Function通过遵循一组简单的规则，定义了在初始化、更新、求导、输出和终止环节如何工作。在每一个环节中，Simulink的引擎都会调用一个方法完成特定的任务。

神经元平衡控制器和神经元速度控制器由MATLAB中的S-Function组件编写。控制系统为离散系统，每0.01 s进行一次信号采样和输出。仿真启动之后，首先进行状态变量的初始化，控制系统在每0.01 s的时间中接收仿真系统的传感器信息，采用BP神经网络算法完成控制系统状态变量的更新和控制量的输出。为方便调节参数，使用示波器模块完成数据的采集和监视。

BP神经网络算法的学习率对算法的效果起着至关重要的作用。BP神经网络算法采用梯度下降的搜索算法，这些算法会先初始化一个解，在这个解的基础上，确定一个搜索方向和一个移动步长，使初解根据这个方向和步长移动后，能使被控系统的误差下降。然后更新出新的解，再继续搜寻下一步的移动方向的步长，这样不断迭代下去，被控系统的误差不断下降，最终能找到一个解，使得误差尽可能地小。在寻求最优解的过程中，步长太大，就会搜索得不仔细，可能跨过更加合适的解；步长太小，又会使得寻解的过程进行得太慢。因此，步长设置适当非常重要。

4 实验

对比PID控制器、神经元PID控制器在二轮平衡车上的控制效果，控制内容包括平衡控制和速度控制。分别在空载和负载下进行实验，其中负载时，物块的质量为100 g。图13所示为仿真系统呈现的二轮平衡车的三维可视化仿真结果。

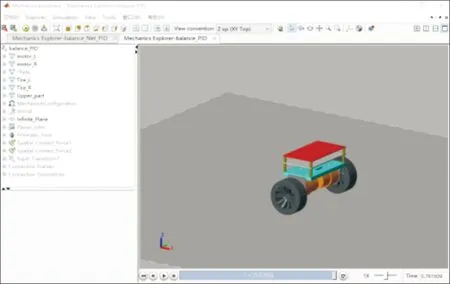
图13 Simcape的三维可视化仿真结果

4.1 空载下控制性能实验

平衡车的平衡性能主要指它站立时，波动范围越小，表明平衡车平衡控制性能越好。同时二轮平衡车轮子的速度变化范围越小，说明二轮平衡车偏离原点的范围越小，即平衡车的速度控制性能越好。

图14所示为空载下神经元PD平衡控制器与传统PD平衡控制器控制平衡车倾角变化过程。可知：神经元PD平衡控制器的倾角在2 s之前波动幅度大于PD控制器，但是随着神经元更新PD参数至收敛值，二轮平衡车的倾角几乎稳定在目标值0；PD平衡控制器的倾角变化幅度始终在-0.5°～0.5°之间，几乎无变化。此时神经元PD平衡控制器的值和值学习过程如图15所示，学习率分别为0.001和0.2。值收敛在0.365，值收敛在0.781。

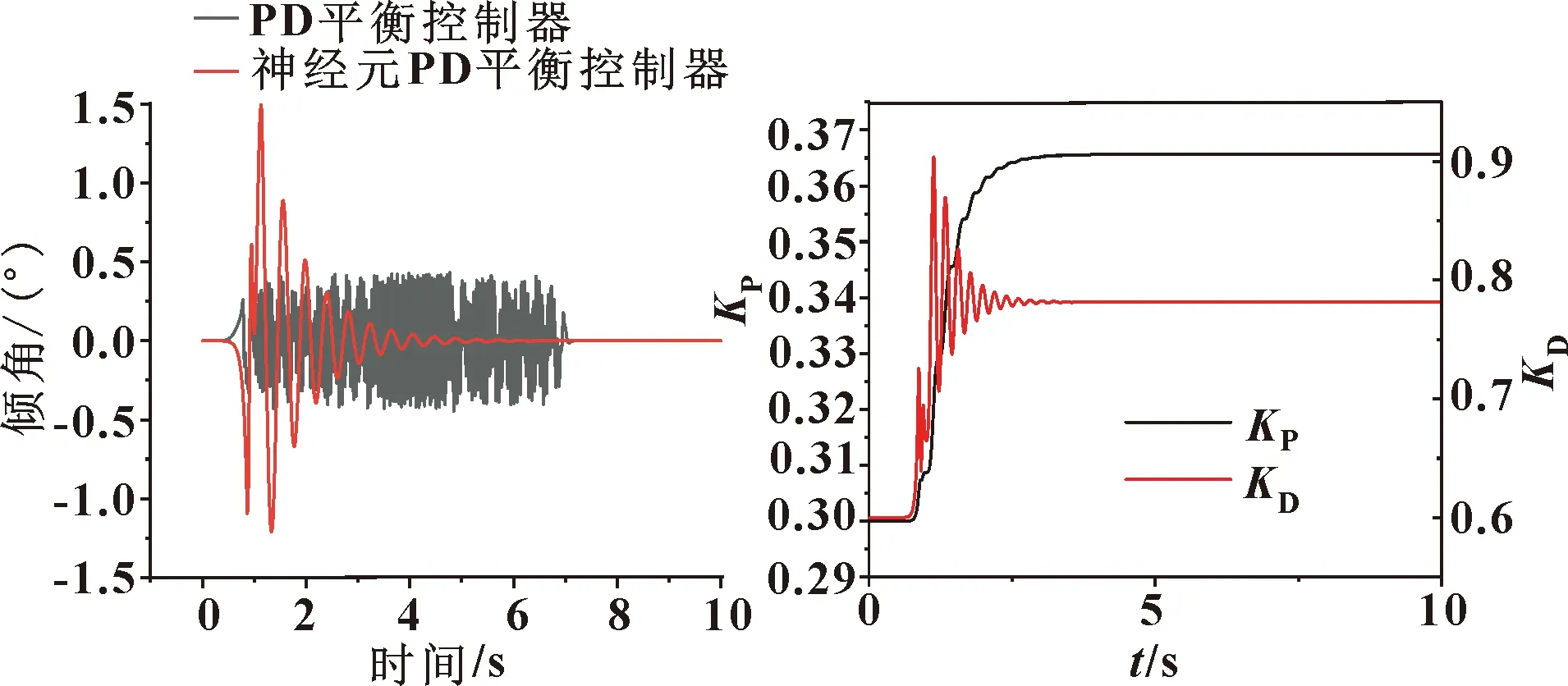
图14 空载下2种控制器倾角变化过程 图15 神经元平衡控制器PD参数迭代

图16所示为神经元PI速度控制器与PI速度控制器控制二轮平衡车速度变化过程。可知：神经元PI速度控制器控制的二轮平衡车速度在刚开始时有大幅度的波动，但是速度的波动幅度始终小于PI控制器，且在大约1.2 s之后，速度变化几乎接近于目标值0；PI控制器控制的轮速始终在-2.5～ 2.5°/s的范围内高频波动。设置神经元PI速度控制器中、参数的学习率分别为0.000 2和0.000 000 1，如图17所示，、的最终收敛值分别为0.011 1和0.000 001 43。

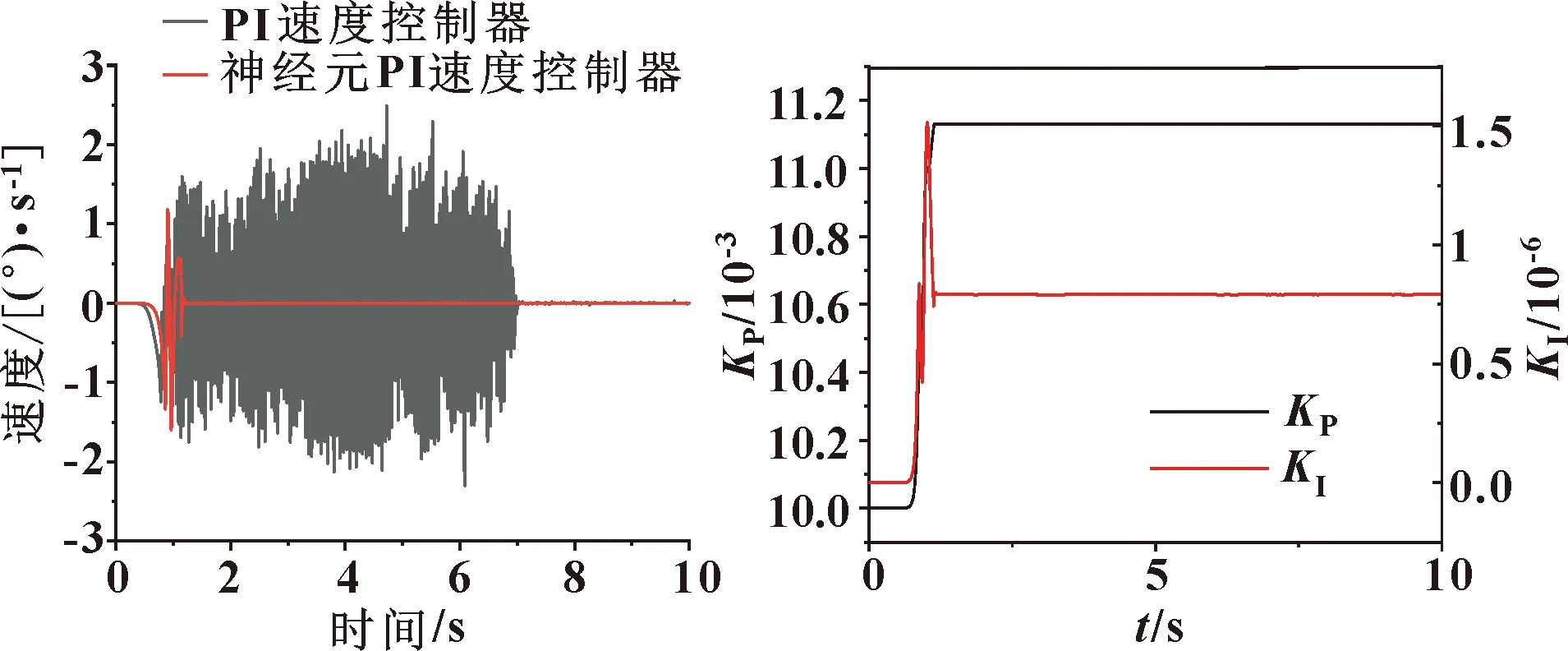
图16 空载下2种控制器速度变化过程 图17 神经元速度控制器PI参数迭代

4.2 负载下控制性能实验

在二轮平衡车上部施加0.1 N垂直向下的力来代表物块。对比神经元PID与传统PID控制的抗干扰能力。二轮平衡车越能够快速地回到稳定状态，且倾角和速度产生波动的范围越小，波动曲线越平缓，控制器的抗干扰性能越好。

图18所示为负载下神经元PD平衡控制器与传统PD平衡控制器控制平衡车的倾角变化过程。可知：神经元PD平衡控制器控制的倾角的波动范围为-2°～2°，而PD平衡控制器的倾角波动范围为-4.5°～4.5°，且波动频率高于神经元PD平衡控制器。神经元PD平衡控制器的抗干扰性能优于PD平衡控制器，但是在干扰结束后，收敛速度慢于PD平衡控制器。此时神经元PD控制器的值和值的学习过程如图19所示，学习率不变。值收敛在0.553，值终值在1.12，根据趋势，随着仿真时间的增加，也必然收敛。

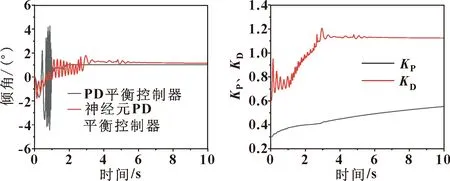
图18 负载下2种控制器倾角变化过程 图19 负载下神经元平衡控制器PD参数迭代

图20所示为负载下神经元PI速度控制器和PI速度控制器控制平衡车速度的变化过程 ，神经元PI速度控制器控制的速度波动范围为0～16°/s，速度波形较为平缓，而PI速度控制器控制的速度波动范围为-17.5～27.5°/s，且波动频率远高于神经元PI控制器。二轮平衡车在神经元PI速度控制器的控制下可迅速地到达目标速度值0。此时神经元PI速度控制器的值和值学习过程如图21所示，学习率不变。可知：值收敛在0.218，值收敛在0.002 07。

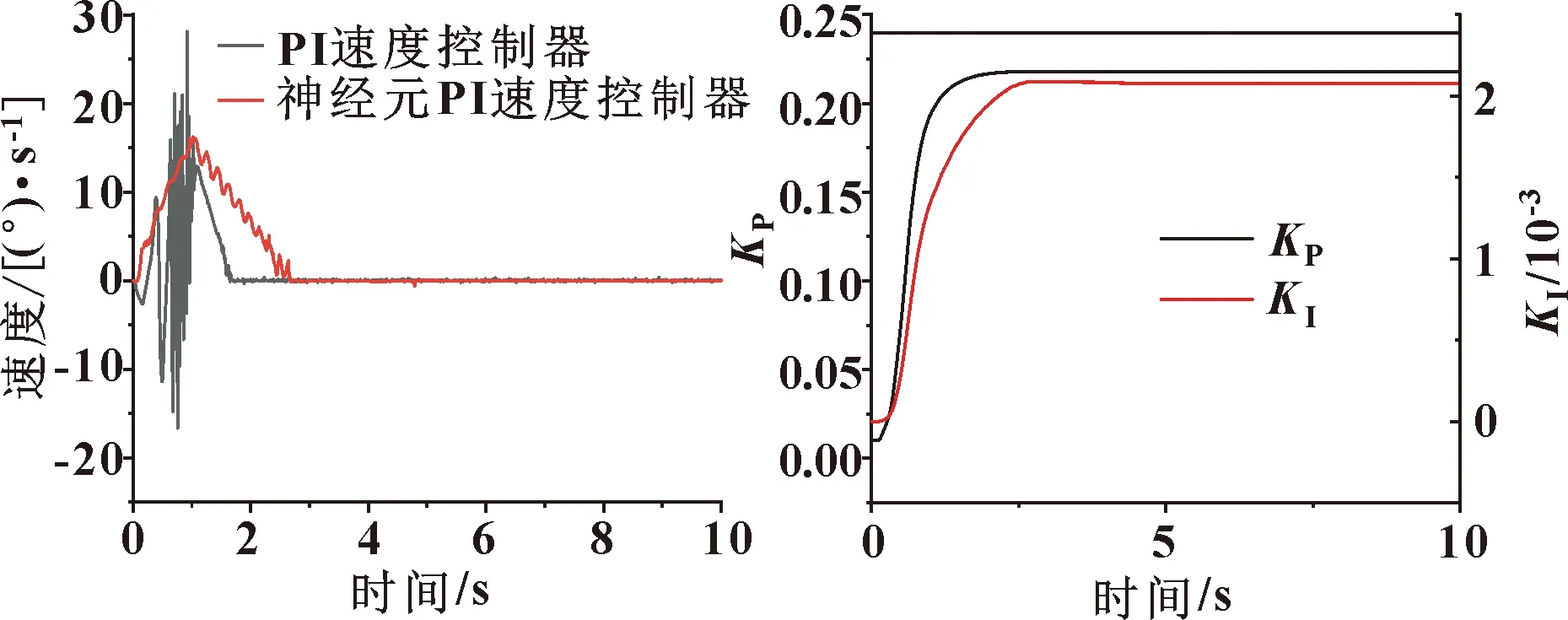
图20 有干扰速度变化过程 图21 神经元速度控制器PI参数迭代

5 结论

本文作者运用MATLAB-Simulink-Simscape-Multibody快速搭建二轮平衡车的三维仿真模型，并使用Simulink搭建控制系统。在S-Function组件中编写神经元PID控制算法来实现倾角控制器、速度控制器和转向控制器，并组合成二轮平衡车的控制器，进行二轮平衡车的平衡控制、速度控制和方向控制。通过空载和负载2个控制性能实验，验证了神经元PID控制器相比传统的PID控制器具有更高的控制精度、更强的抗干扰能力、更快的响应速度、更能适应模型的非线性变化。相对于传统PID控制器，采用神经元PID控制器的二轮平衡车在平衡控制和速度控制上都有具有更好的性能。