冲击载荷下液压支架再制造立柱强度分析

钟宏宇， 吕凯波， 樊红卫，李健 ，苏成明 ，高宏伟

(1.太原理工大学机械与运载工程学院，山西太原 030024；2.西安科技大学机械工程学院，陕西西安 710054；3.太原理工大学霍州智能再制造研究院，山西临汾 041000；4.陕西天元智能再制造股份有限公司，陕西西安 710065)

0 前言

液压支架是煤矿综采工作面的重要设备，为井下开采提供安全的作业空间。双伸缩立柱是液压支架的主要承载部件，起着调节支架高度、维持支架平衡、缓冲过载冲击等作用。立柱由于受载大，工作在腐蚀、粉尘等恶劣环境下等因素，通常会出现表面锈蚀、划伤等失效形式，导致密封性下降，出现漏液，使得液压支架功能丧失。如果将这些失效的立柱报废处理会造成资源的极大浪费，因此对其进行再制造有着显著的经济效益和环境效益。

传统的立柱再制造方式是电镀镀铬，修复后镀层与母材结合力不强，容易鼓包造成脱落，使用寿命短。激光熔覆是一种新兴的再制造技术，运用此种方式修复后的立柱有着硬度高、抗腐蚀、耐磨损等优点。经过激光熔覆再制造修复的立柱在重新投入使用前需要进行可靠性检验，目前通常使用的检验方法是实验法，较为耗时耗力。

随着计算机仿真技术的发展，有限元方法在液压支架立柱设计和强度分析中得到了广泛的应用。WANG等基于混合结构和非结构有限元网格对360型双伸缩立柱进行了轴向1.5倍、2.0倍额定载荷以及偏心1.1倍额定载荷的有限元分析，得到在不考虑动荷载的情况下，立柱可承受2.0倍轴向压力和1.1倍偏心0.3压力，应力加载均匀，荷载传递合理的结论。郭永昌、廉自生利用机械振动原理建立320型单伸缩立柱的冲击模型，建立立柱的ANSYS有限元模型进行瞬态动力学仿真，为立柱在动载荷下的冲击强度分析提供一种可行的计算分析方法。董良太利用有限元分析软件对立柱进行2倍中心载荷情况下强度分析和流固耦合分析，为液压支架立柱的设计提供了参考依据。

以ZY12000-28-63D液压支架的400 mm双伸缩立柱为研究对象，根据GB 25974.2—2010《煤矿用液压支架第2部分:立柱和千斤顶技术条件》，基于重锤法来模拟液压支架受到冲击载荷的工况，推导计算出立柱受冲击时各级缸体内部最大液体压力。建立再制造立柱限元模型，基于有限元法得到各级缸体及熔覆层的应力结果，分析不同激光熔覆工艺参数对立柱缸体强度的影响规律。研究为再制造立柱的可靠性检验提及熔覆工艺参数选取供理论参考。

1 冲击载荷下立柱内液体压力计算

立柱受到冲击载荷的过程可以用落锤加载法模拟，如图1所示。此方法简单易行，还可以通过改变落锤的高度和质量来模拟实际工况。在重锤下落冲击立柱的过程中，忽略缸体间较小的摩擦阻尼，将双伸缩立柱等效为两级轴向弹性体串联。重锤从距离活柱顶端2 m的高度向初撑力=3 600 kN的立柱落下，与活柱接触后一起向下运动，当运动的距离达到最大时缸体内液体压力也达到最大。立柱几何参数如表1所示。

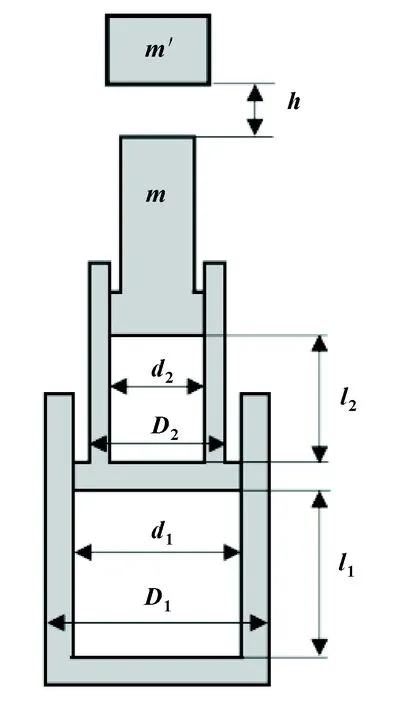
图1 重锤冲击模型

表1 立柱几何参数

为获得缸内最大压力需求得立柱的等效刚度，该等效刚度与缸内乳化液的容积弹性模量有关。

由刚度定义得，双伸缩立柱(=1时为立柱外缸，=2时为立柱中缸)级缸体等效刚度：

(1)

式中：为第级缸内径所在圆面积,m；为第级缸有效液柱长度,m。

容积弹性模量定义

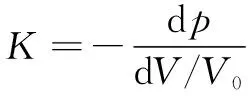
(2)

式中：为乳化液的初始体积，m。

考虑缸径变化的乳化液容积弹性模数：

(3)

式中:为第级缸体外径，m；为第级缸体内径，m；为缸体材料弹性模量，=206×10MPa；为泊松比,=026；为5乳化液容积压缩系数，=55×10m/N。

由式(2)(3)可得各级缸体等效刚度：

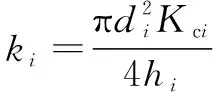
(4)

由弹性体串联刚度可得双伸缩立柱等效刚度：

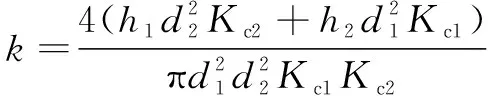
(5)

由能量法可得，重锤与活柱接触后向下运动的最大距离：

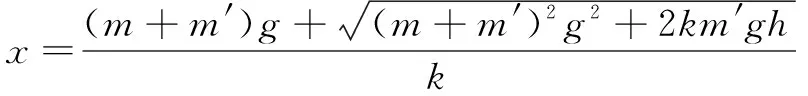
(6)

式中：为活柱质量，=641 kg；′为重锤质量，′=15 000 kg。

立柱内有初撑力各级缸内最大液体压力：

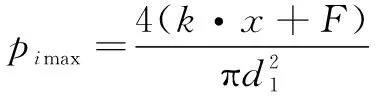
(7)

经计算:=70.49 MPa，=134.11 MPa。

2 再制造双伸缩立柱强度分析

2.1 再制造立柱三维模型建立

再制造双伸缩立柱的主要结构包括外缸、中缸、活柱、熔覆层、导向套和密封圈等零部件。为了方便后续有限元网格划分和仿真计算，需对双伸缩立柱的几何结构进行合理简化。简化时应当遵守以下原则：去掉油孔、底阀等对立柱整体承载能力影响较小的结构；各级缸体均由锻件焊接而成，通常情况下焊缝强度高于母材强度，因此在几何模型建立的过程中忽略焊缝，将双伸缩立柱建立为整体模型。

用NX12.0软件分别建立活柱、中缸、外缸以及熔覆层模型，立柱的再制造工艺为活柱外表面、中缸内外壁以及外缸内壁熔覆不锈钢粉末，熔覆层厚度均为1 mm。因此在建立三级缸体模型时要在保证缸径不变的情况下建立熔覆层。为了便于在有限元软件中赋予基体和熔覆层不同的材料，不对缸体和熔覆层进行布尔运算。再制造立柱几何模型如图2所示，中缸局部放大示意如图3所示。

图2 再制造立柱几何模型

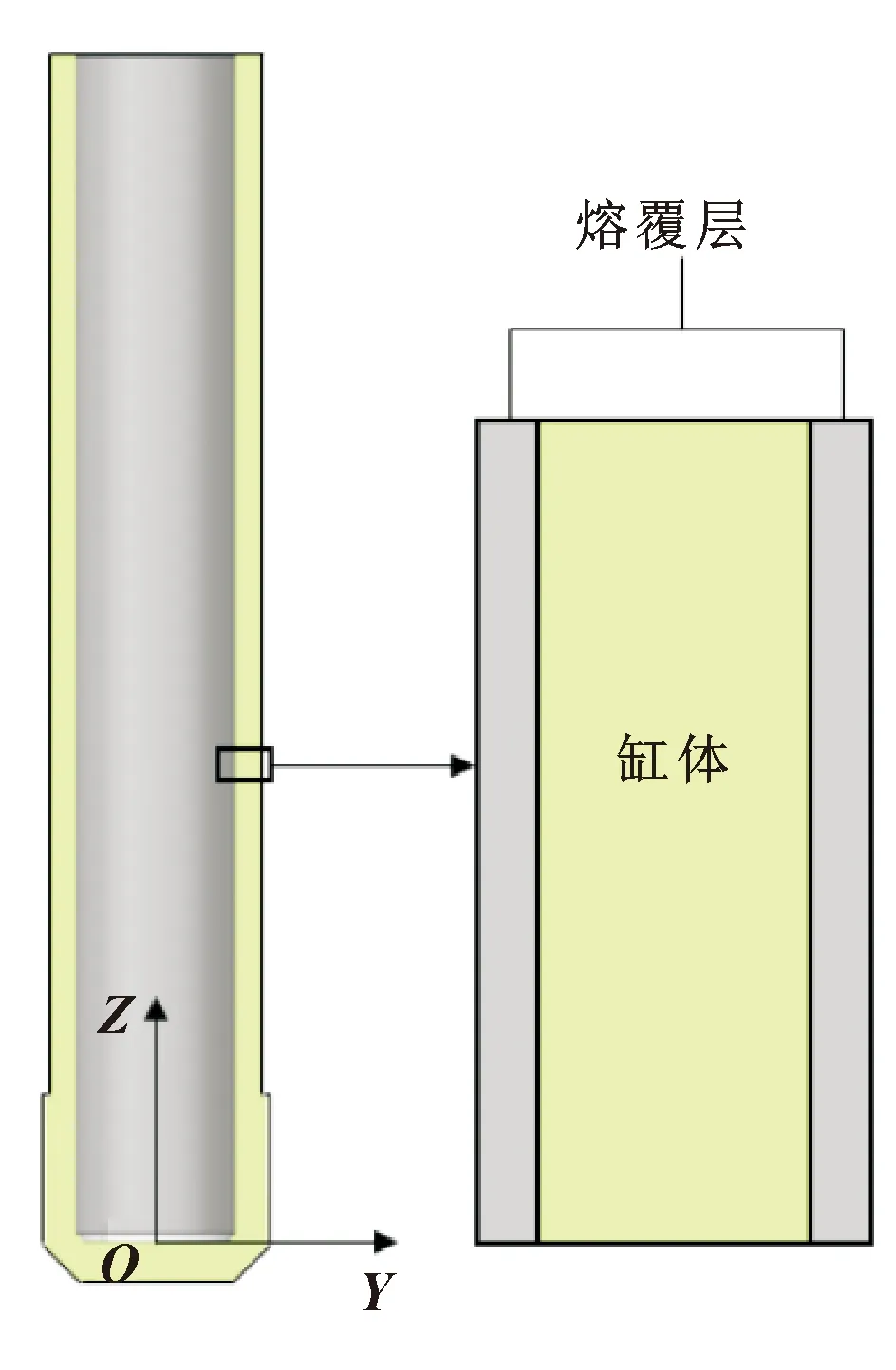
图3 中缸局部放大示意

2.2 有限元分析

立柱基体的材料为27SiMn钢，熔覆层材料为不锈钢粉末，材料的属性如表2所示，不锈钢粉末的屈服强度为条件屈服强度()，为实验测得。

表2 材料属性

文中主要考虑液体压力对缸壁、熔覆层的影响，忽略各级缸体之间的相互作用力。为了便于压力加载和结果分析，将外缸、中缸、活柱分别进行有限元计算。

用ANSYS静力学模块进行有限元分析。为了设置更加准确的边界条件，建立顶梁柱窝与底座柱窝的简化模型并将其分别与活柱、外缸进行装配，将装配体导入ANSYS软件中。首先进行边界条件的设置，将底座柱窝及顶梁柱窝设置为固定约束，外缸缸底、活柱柱头与柱窝之间的接触关系设置为“摩擦”，摩擦因数为0.2，中缸的边界条件为缸底固定约束。将熔覆层与各级缸体之间的接触关系设置为“绑定”。基体与熔覆层均采用四面体网格，单元尺寸设置为15 mm，并对缸体厚度方向以及熔覆层的网格进行细化，保证缸体厚度方向上至少有三层单元。最后进行载荷设置，在外缸、中缸内壁分别加载70.49、134.11 MPa的压力，在活柱底端加载134.11 MPa的压力。各级缸体有限元模型如图4所示。

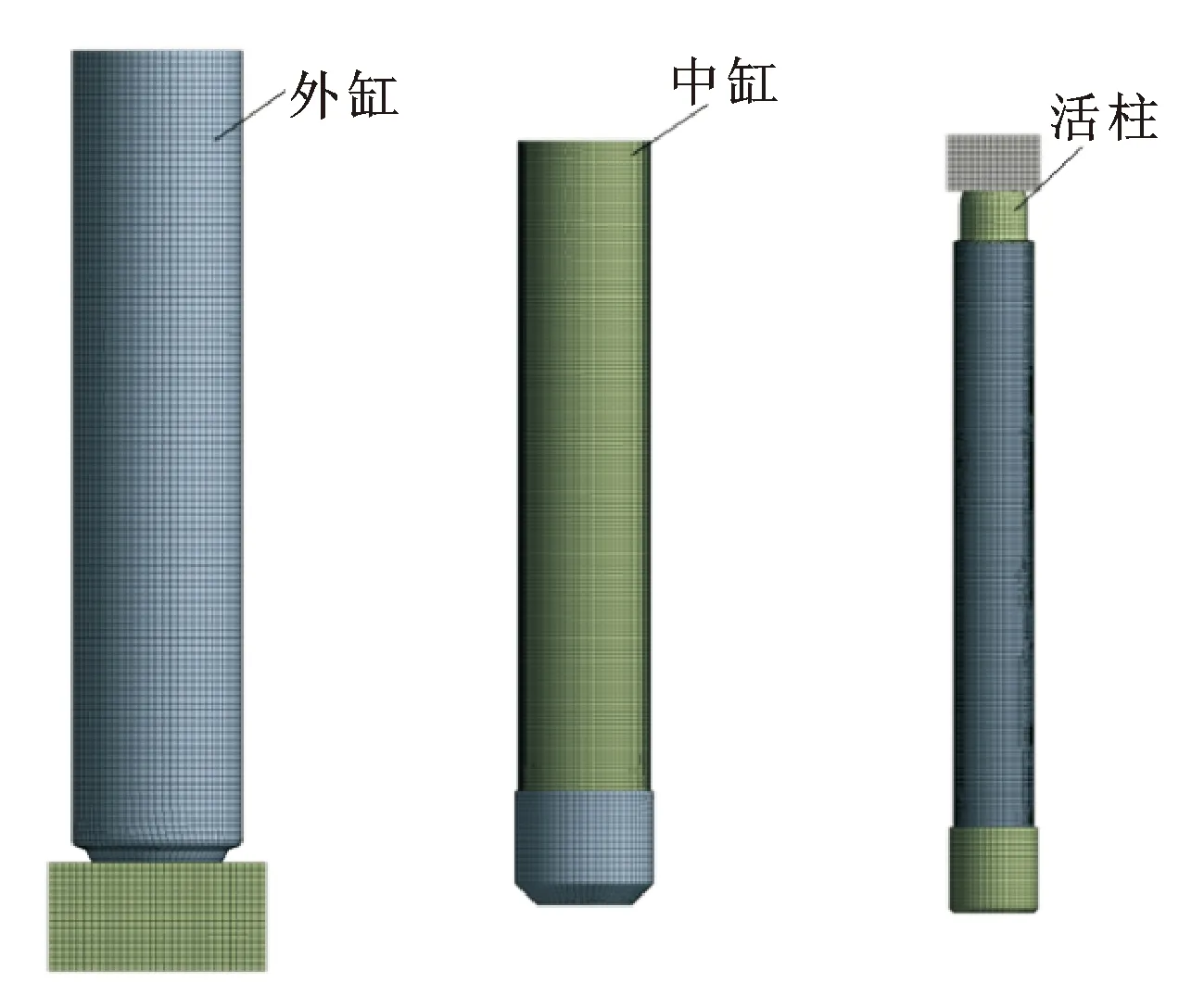
图4 各级缸体有限元模型

2.3 分析结果

根据上述设置对400 mm再制造双伸缩立柱进行有限元分析，得到外缸、中缸、活柱基体及其熔覆层的应力结果分别如图5—图7所示。

图5 外缸应力云图

图6 中缸应力云图

图7 活柱应力云图

由有限元结果得：在上述冲击载荷下外缸、中缸、活柱最大应力分别为503.07、603.03、594.88 MPa，均小于材料27SiMn钢的屈服极限；中缸内壁熔覆层应力较大，最大应力达到570.82 MPa，超过了材料的条件屈服强度()，其余部位熔覆层应力均小于材料的屈服强度。

3 不同熔覆工艺参数对强度的影响分析

由上述结果可知，中缸体内壁厚度为1 mm、材料为不锈钢粉末的熔覆层局部应力大于材料的屈服强度，存在开裂、脱落的风险。为了得到合适的立柱激光熔覆再制造工艺参数，以双伸缩立柱的中缸为对象，基于有限元方法研究熔覆层参数以及熔覆过程工艺参数对强度的影响。

3.1 熔覆层厚度

为研究熔覆层厚度对强度的影响，保证缸径不变，建立熔覆层厚度为1.5、2 mm的再制造中缸三维模型，对其进行有限元分析。沿中缸轴线方向(参看图3)，提取不同位置处内壁熔覆层应力分布，结果如图8所示。

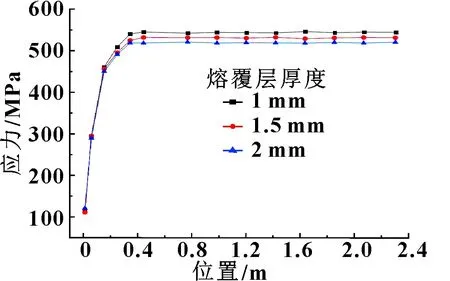
图8 不同厚度熔覆层内壁应力分布曲线

由于缸体和熔覆层为对称结构且载荷均匀分布，因此沿缸体方向上的应力可以较好地反映熔覆层整体应力分布结果。由图8可知：中缸体内壁熔覆层上应力从底部到顶部逐渐增大后趋于平稳，应力随熔覆层厚度增大而减小。

3.2 弹性模量

为研究材料弹性模量对熔覆层强度的影响，以熔覆层厚度为1 mm的中缸为对象，分别设置材料的弹性模量为1.1×10、1.5×10、1.9×10MPa进行有限元分析。沿中缸轴线Z方向(参看图3)，提取不同位置处内壁熔覆层应力分布，结果如图9所示，由结果可得应力随弹性模量的减小而减小。

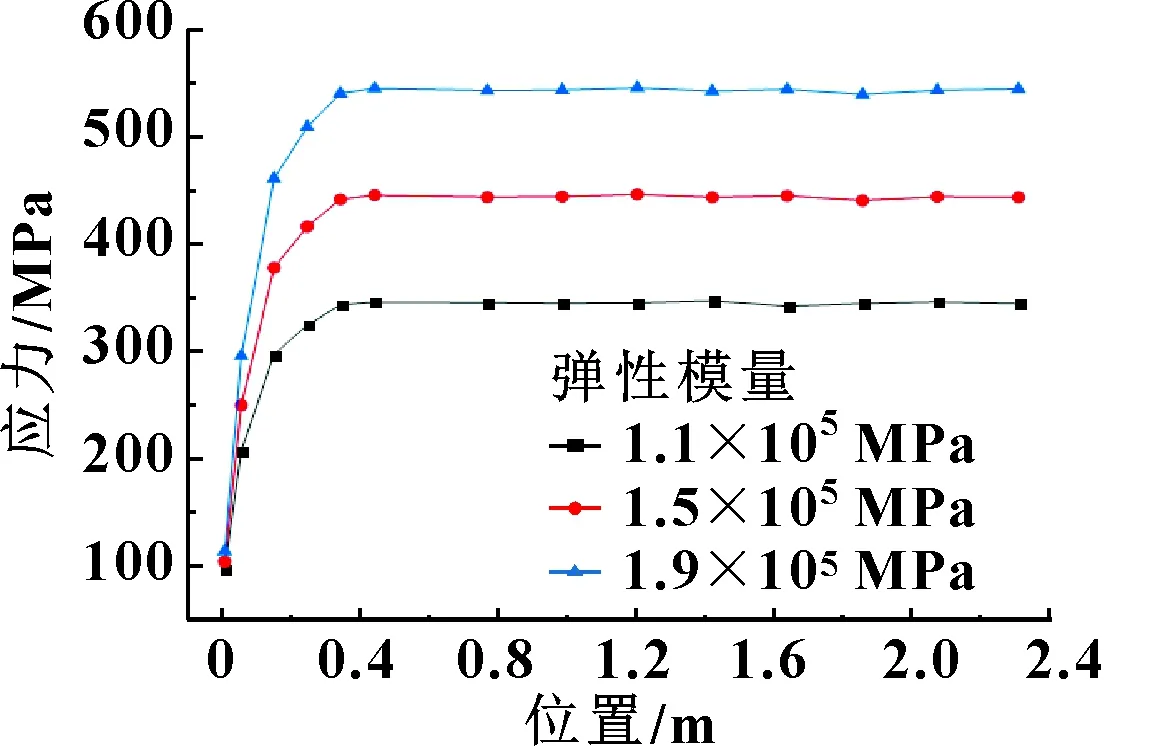
图9 不同弹性模量熔覆层应力分布曲线

3.3 激光功率

激光熔覆过程中极易形成残余应力，且残余应力为拉应力。而立柱在受到冲击载荷时同样产生拉应力，熔覆过程产生的残余应力将直接影响再制造立柱的强度。

建立单道熔覆层和立柱基体有限元模型，其中基体的尺寸为50 mm×50 mm×15 mm，熔覆层的厚度为1 mm。用高斯热源模型来模拟实际熔覆过程中激光热源的输入，高斯热源模型的表达式如下：

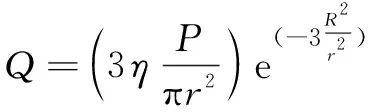
(8)

式中：为光斑内任意点的热流密度；为激光利用率；为激光功率；为激光光斑半径；为任意点到热源中心的距离。令热源沿着铺粉方向移动，则的表达式为

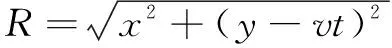
(9)

式中:为热源移动速度。

由于熔覆材料和基体材料的导热系数、密度和比热容等热物性参数随温度而变化，根据文献[15]设置材料的热物性。设置激光功率为1 600 W，激光扫描速率为10 mm/s，光斑直径为5 mm，初始温度为22 ℃。基于ANSYS瞬态热分析模块对不同激光功率熔覆过程进行数值模拟，将得到的温度场结果作为载荷对模型加载，进行热力耦合的应力场计算，残余应力结果如图10所示。

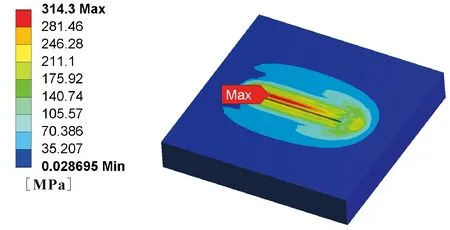
图10 残余应力分布图

保持其他条件不变，改变激光功率进行热力耦合的应力场分析。沿缸体截面厚度方向(参看图3)，提取距熔覆层表面不同深度处的应力分布，结果如图11所示。

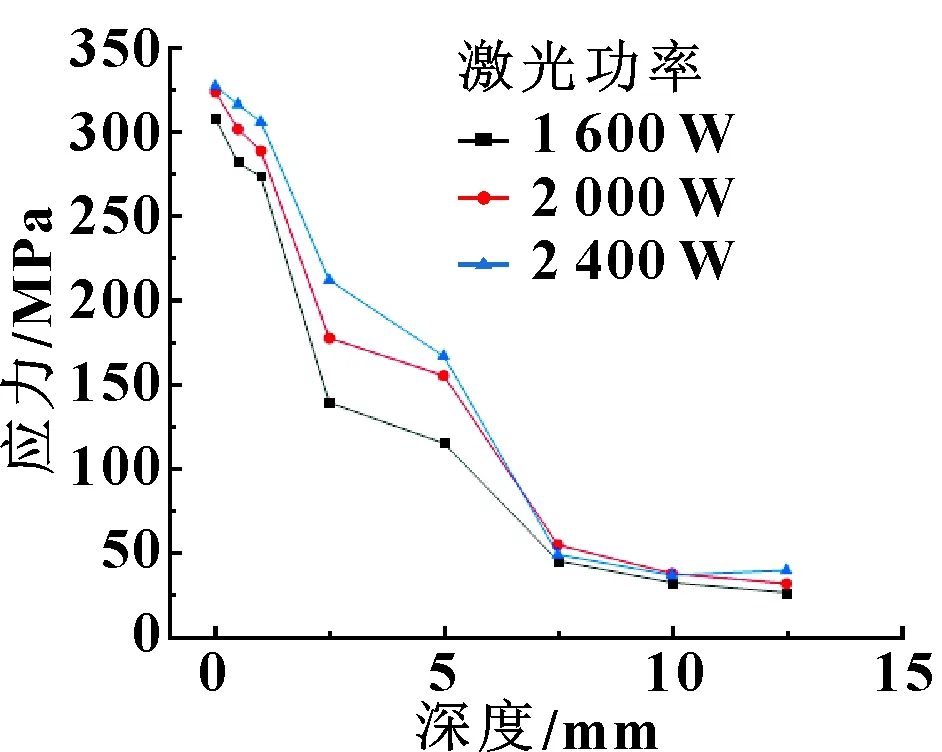
图11 不同激光功率下Y方向应力分布曲线

由图10可知：激光熔覆过后基体和熔覆层均产生了残余应力，其中熔覆层表面的残余应力较大，功率为1 600 W时最大应力达到314.3 MPa。由图11可知：残余应力从熔覆层表面到基体底面总体呈现减小趋势；并且随着激光功率的减小，基体和熔覆层的残余应力均减小。

4 结论

推导了400 mm双伸缩立柱受冲击载荷时的等效刚度，计算了15 000 kg的重锤从2 m高度自由落体冲击立柱时各级缸体最大液体压力，基于有限元法对再制造立柱强度以及熔覆工艺参数对强度的影响进行了分析，得到主要结论如下：

(1)在冲击载荷作用下，400 mm再制造双伸缩立柱最大应力为603.03 MPa，出现在中缸内壁。各级缸体应力均小于基体材料27SiMn钢的屈服极限835 MPa。激光熔覆层最大应力为570.82 MPa，出现在中缸内壁不锈钢粉末熔覆层上，大于材料的条件屈服强度()551 MPa，容易产生裂纹，其余部位熔覆层的应力均小于对应材料的条件屈服极限。

(2)熔覆层应力随其厚度的增大而减小；应力随熔覆层弹性模量的增大而增大；熔覆过程产生的残余应力随激光功率的增大而增大。因此可以通过增大熔覆层厚度、使用弹性模量更小的材料进行熔覆或减小熔覆过程激光功率来提高再制造立柱的强度。