一种考虑三线摆摆线质量的转动惯量计算方法及虚拟验证

祝恒佳，邝晨阳，吕晓

(1.中国民航大学航空工程学院,天津 300300；2.中国民航航空地面特种设备研究基地，天津 300300)

0 前言

三线摆法作为测量物体转动惯量的基本方法之一，因其相对简单的实验原理和较精确的测量结果而被广泛应用。在车辆、航空工程领域，发动机总成转动惯量直接影响隔振系统设计、结构件疲劳寿命分析，针对刚体转动惯量的准确测量具有重要意义。

三线摆由上盘、下盘和3根连接上下盘的摆线组成。在实验时，先使下盘绕质心轴偏转一个微小角度，而后释放使其自由运动，测出扭摆周期，根据保守系统的机械能守恒定律，计算下盘绕质心轴的转动惯量。

通常在使用三线摆时会将其视为理想三线摆，摆线为轻质摆线，忽视其惯性参数对测量结果的影响。三线摆类似于单摆，其运动方程并非线性微分方程。而为了计算方便，常常将方程中的正弦函数近似一阶线性化处理。对于理想三线摆，摆线长度越长，扭摆时下盘在竖直方向上的位移越小，依据相关的公式，不难得出摆长越长，精度越大的结论。但现实中摆线存在质量，若将绷直的摆线视为均质的刚性杆，其轴向的转动惯量很小，而径向的转动惯量很大，在扭摆过程中摆线将获得一部分机械能，并且摆线越长，其在系统中所占机械能比重也越大，对测量结果造成的误差也随之增大。当摆线对测量造成的影响不可忽略时，应针对摆线的影响具体分析。

为了解决三线摆的测量误差问题，现有的办法是在搭建三线摆之后对三线摆进行标定，改进三线摆的参数。根据唐晓峰给出的标定方法，选用两个已知惯性参数的标准质量块置于下盘，使其质心与上下盘质心共线，分别测出扭摆周期，进一步可获得改进后的下盘质量和摆长。胡志强和胡勇搭建了测量动力总成的三线摆，对标定的结果进行了验证，证实使用标定后的参数计算的转动惯量的误差均可达到1%以下。PREVIATI采取标定非线性微分方程参数的方法，将运动方程用泰勒公式展开到四阶，用最小二乘法求得该三线摆在特定摆幅下的转动惯量计算公式；经过实验验证，该方法同样能将误差控制在1%以下，且对于大摆角振荡同样具有很高的精确性。以上方法只针对特定的三线摆进行标定，更换三线摆后需要重新标定，并没有深入讨论摆线在三线摆系统中能量转化层面的影响。并且PREVIATI的方法较为复杂，在小摆角的实验中，运动方程高阶展开带来的精度提升并不显著。葛宇宏、葛志利首次研究了摆线质量对测量的影响，从能量的角度对摆线的运动进行近似分析，通过哈密顿原理推导了包含摆线参数的转动惯量计算公式，证明其公式对精度的提升作用。一般物理实验使用的三线摆通常尺寸较小，使用细金属丝作为摆线材料，摆线质量可以忽略不计。而发动机动力总成质量多为几百公斤，在设计三线摆时通常会选用钢丝绳作为摆线材料，其长度和密度均很大，势必会对测量产生影响。

本文作者将采用不同于葛宇宏等的方法研究摆线的运动，将摆线视为直径足够小的刚性杆，从能量守恒的角度推导出考虑摆线质量参数的刚体转动惯量测量的改进公式，与葛宇宏等的计算方法相比更为简便。本文作者还研究了一种可行的三线摆建模方法，采用虚拟样机技术在ADAMS/View环境建立三线摆虚拟实验平台，使用该模型对文中提出的测量改进方法进行验证，并进一步研究了摆线的线密度和长度对测量误差的影响规律。

1 改进的三线摆测量方法

1.1 不考虑摆线的计算方法

刚体惯性参数三线摆测量模型的原理如图1(a)所示，和分别表示上盘和下盘半径，为上下盘圆心距离，3根摆线的长度均为，且悬挂点之间以120°角分布。测量前，将三线摆下盘转过微小角度，此时下盘上升微小高度，如图1(b)所示，可得

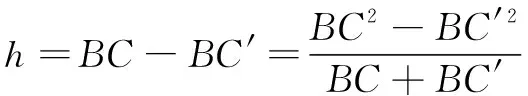
(1)

式中：

=-=-(-)

(2)

′=′-′′=-(+-2cos)

(3)

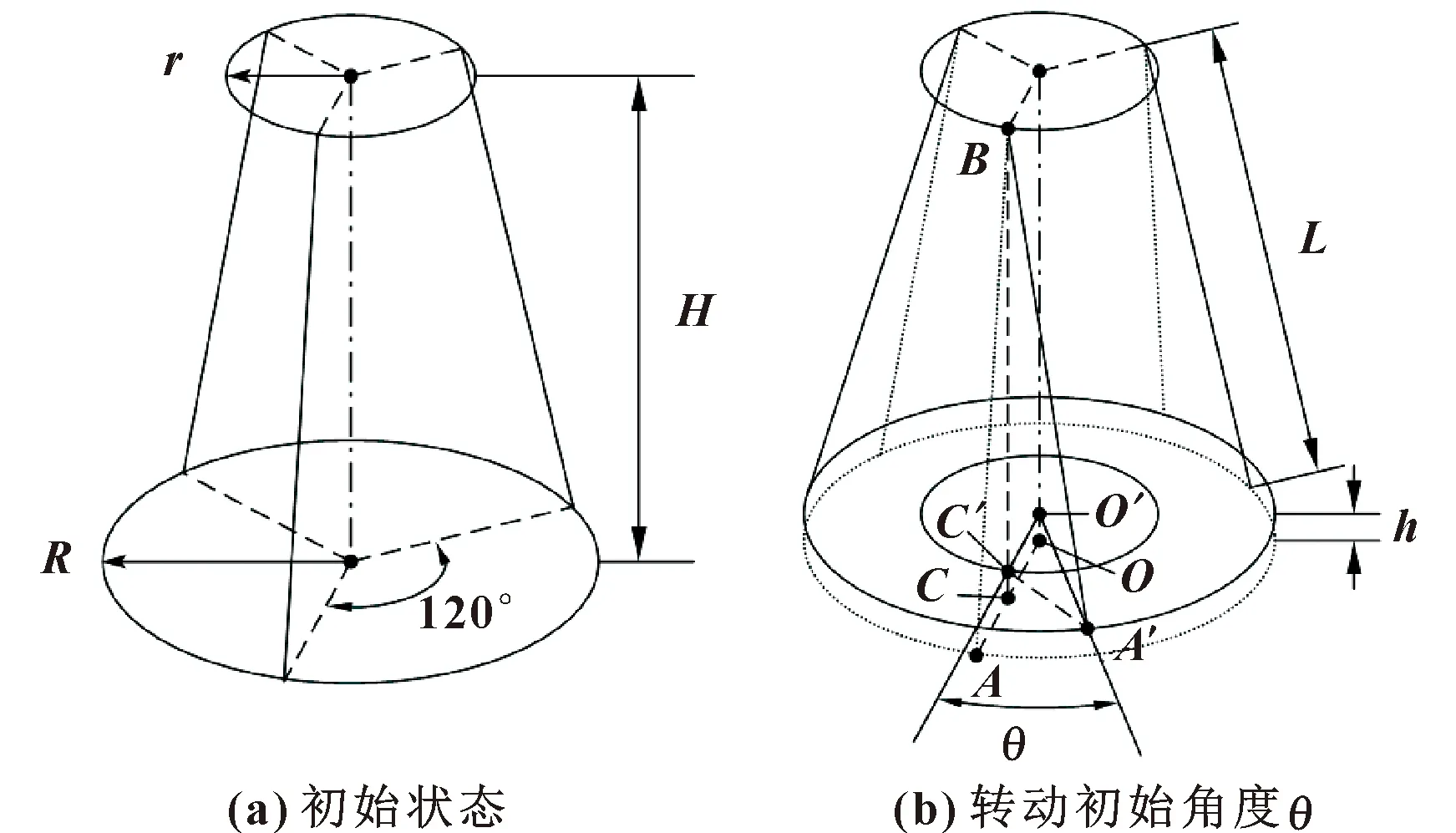
图1 三线摆模型示意

对于分母项，由于微小高度远小于，可得

+′=2-≈2

(4)

将式(2)—式(4)代入式(1)，则

(5)

忽略空气阻力，将三线摆系统视为保守系统，在扭摆过程中机械能守恒，定义平衡位置的势能为0，忽略扭摆过程中竖直方向的平动动能，列出能量守恒公式

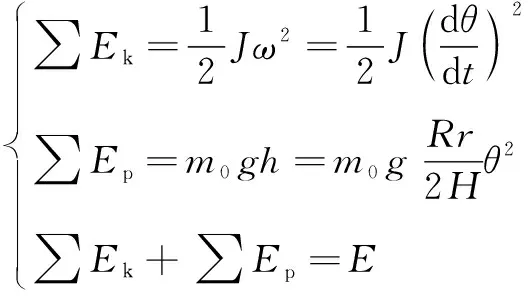
(6)

式中：表示下盘关于质心的转动惯量；表示下盘的质量；为机械能常数。当下盘转到最大转角，此时动能∑=0，势能∑达到最大，根据式(5)中和的关系，有

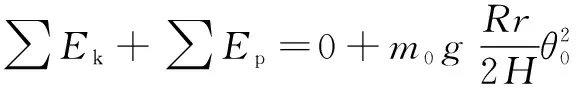
(7)

联立式(6)和式(7)，将d单独放在等式左边，可得

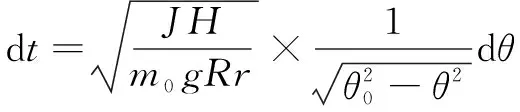
(8)

对式(8)两边积分，得到周期的计算公式

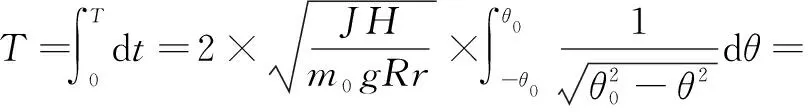
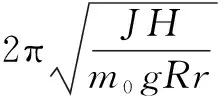
(9)

整理可得实验中被测刚体的转动惯量

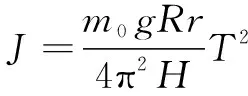
(10)

实验测量中需测量空载时下盘回转周期，从而计算下盘的转动惯量；然后测量带被测物体下盘的周期，由此算出下盘和物体总转动惯量，减去下盘的即为被测物体的转动惯量

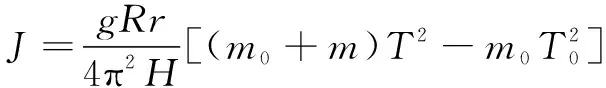
(11)

式中：为被测刚体质量；为下盘质量；为物体关于质心的转动惯量。在测量时应确保被测刚体质心位于下盘的旋转轴线上，如图2所示。

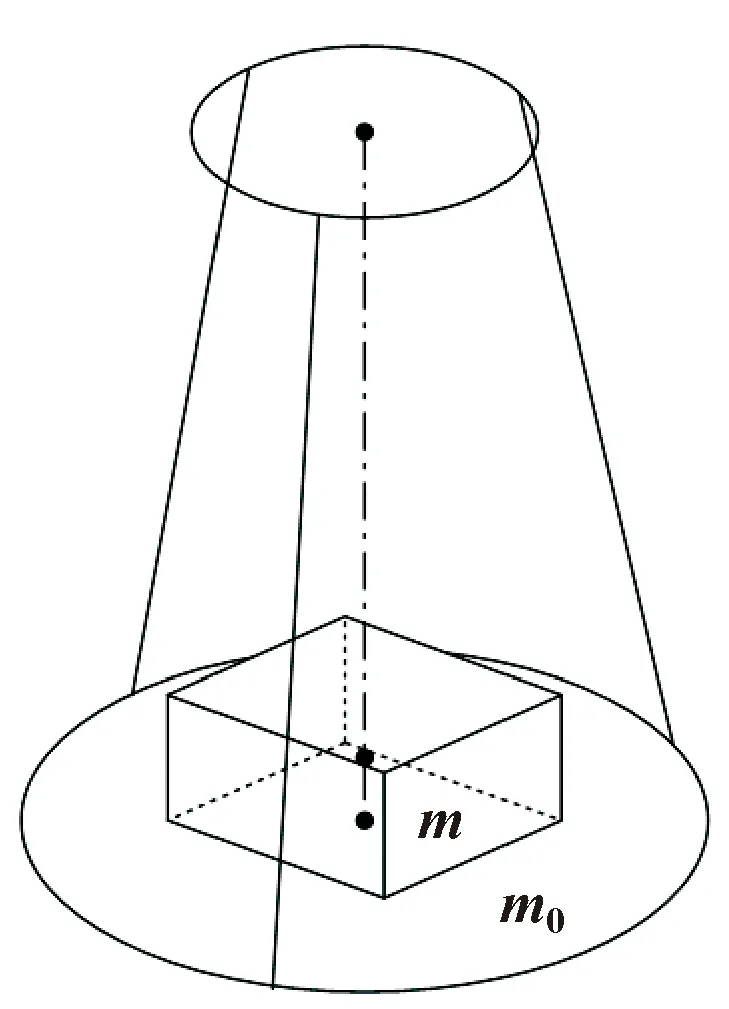
图2 三线摆实验简图

1.2 考虑摆线的计算方法

当被测刚体较大，为了满足承载要求，摆线可能设计得较粗，此时摆线质量对被测刚体转动惯量测量结果的影响不能忽略。考虑在低速运动状态下，摆线始终保持拉伸绷直状态，可将摆线当做杆进行分析计算，摆线上的各点速度大小呈线性分布，如图3所示，最下端点的速度即为下盘外径线速度，最上端点与上盘连接，速度为0。在微小摆角的情况下，认为速度方向始终垂直于杆方向。下盘摆动角速度为，半径为，有

=

(12)

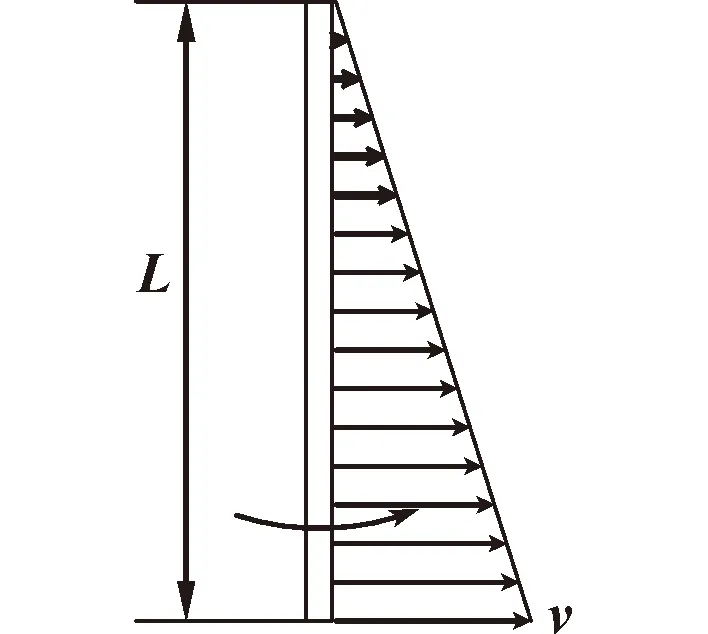
图3 摆线速度分布

设杆的线密度为，微元d的动能为

(13)

当下盘转过角度，微元的重力势能为

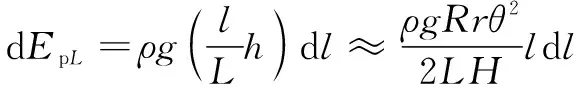
(14)

对式(13)和式(14)两边积分，得到单根摆线的动能和势能分别为

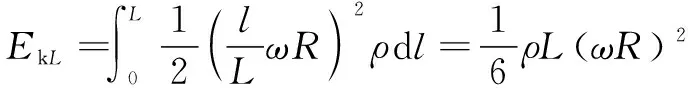
(15)

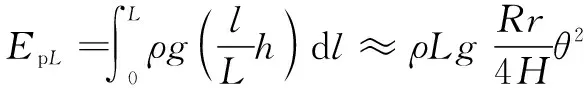
(16)

综上，列出能量守恒公式

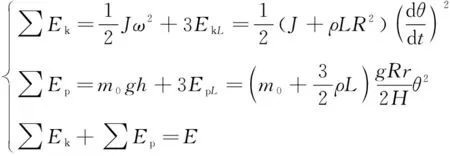
(17)

当下盘转动到最大角度，此时动能∑=0，势能∑达到最大，有

(18)

类似地，联立式(17)和式(18)并积分，整理可得改进后的被测刚体转动惯量为

(19)

实际测量物体时需要测量空载和负载两种情况下周期，与上一小节所述方法类似，被测物体的转动惯量为

(20)

和式(11)相比，式(20)在计算被测刚体转动惯量时考虑了摆线参数的影响，其中“”表示单根摆线的质量。

2 ADAMS仿真虚拟验证

2.1 三线摆虚拟样机模型

如图4所示，在ADAMS/View中建立三线摆虚拟样机测试平台，上盘和下盘材质均匀分布，半径均为600 mm，上下盘间距6 000 mm，通过3根摆线相连接，摆线连接点在上下圆盘上呈120°分布。李永波、魏禹将圆柱形绳索离散为若干小段通过弹性衬套相互连接，研究绳索的动力学特性。摆线用Cable模块进行建模，由于该模块要求绳索至少需要穿过1个滑轮，故将3个滑轮固定于上盘，3根Cable上端连接于上盘中心位置并与上盘固定，如图5所示。滑轮与Cable上半段跟随上盘运动，实际上不因参与扭摆而影响测量结果。设计下盘最大载质量1 000 kg左右，所需摆线最小破断拉力大于10.2 kN。选用钢丝绳作为摆线材料，根据GB/T 9944—2015可知公称直径8.0 mm的6×19-WSC钢丝绳最小破断拉力为36.1～40.1 kN，参考质量为25.8 kg/100 m，具体参数见表1。

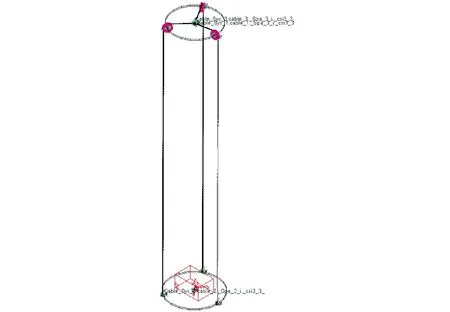
图4 三线摆虚拟样机模型

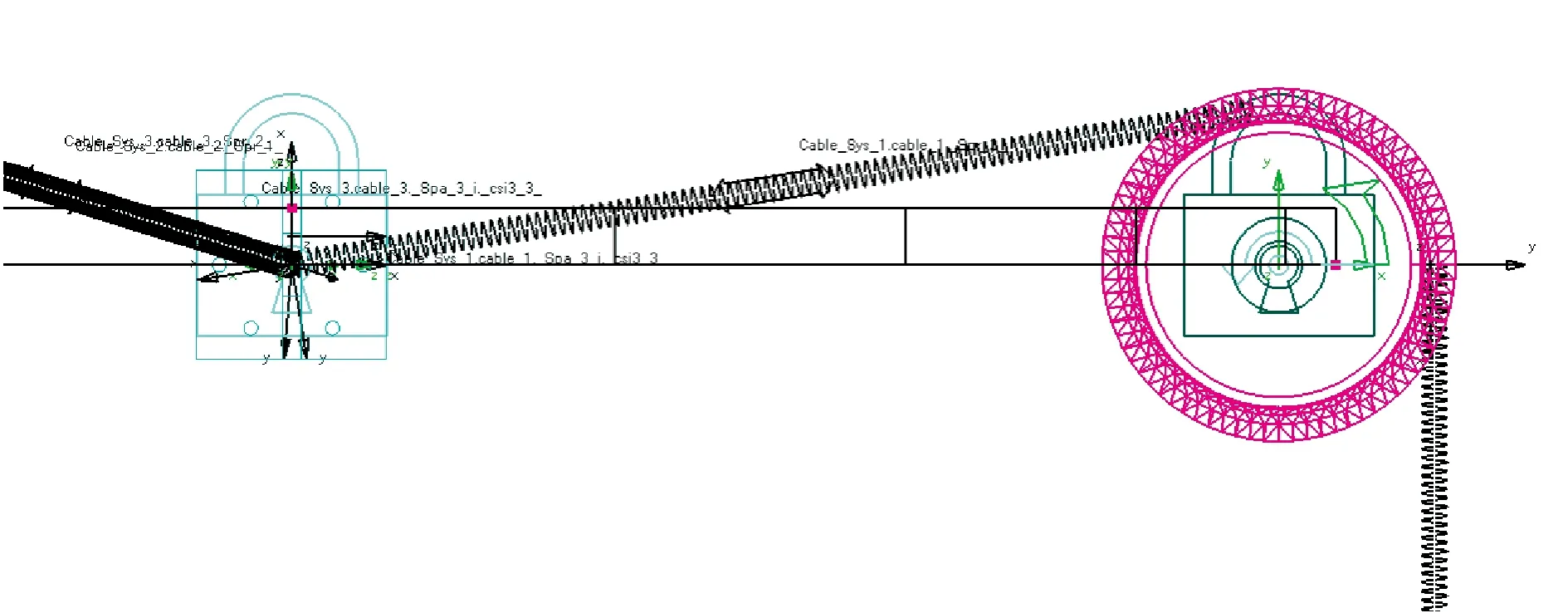
图5 滑轮-绳索建模

表1 三线摆参数

被测刚性质量块的质心位于下盘轴线上，如图6所示。从模型中能直接获取其惯性参数作为基准值：质量=561.672 kg，关于质心轴的转动惯量=2.434×10kg·mm，以此对此改进的三线摆测量方法进行验证。考虑小角度下的扭摆情况，令=5°，设置步长0.001 s。在上盘的质心处添加一个旋转驱动，设置阶跃函数，使上盘在0.1 s内产生5°的角位移，带动下盘扭摆，获取空载和负载两种工况下的扭摆周期和，由此计算物体的转动惯量。

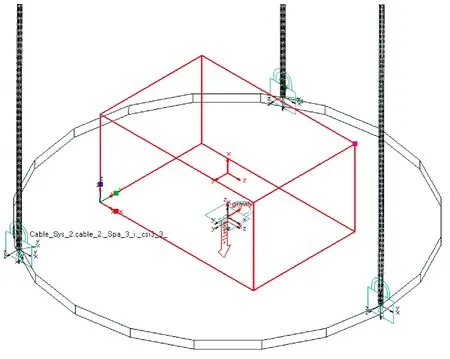
图6 被测刚体质量块模型

2.2 三线摆测量仿真分析

(1)不考虑摆线惯性

将Cable参数中的Inertia开关设为off，此时摆线质量为零即=0，仿真得到下盘角位移-时间曲线,如图7所示。

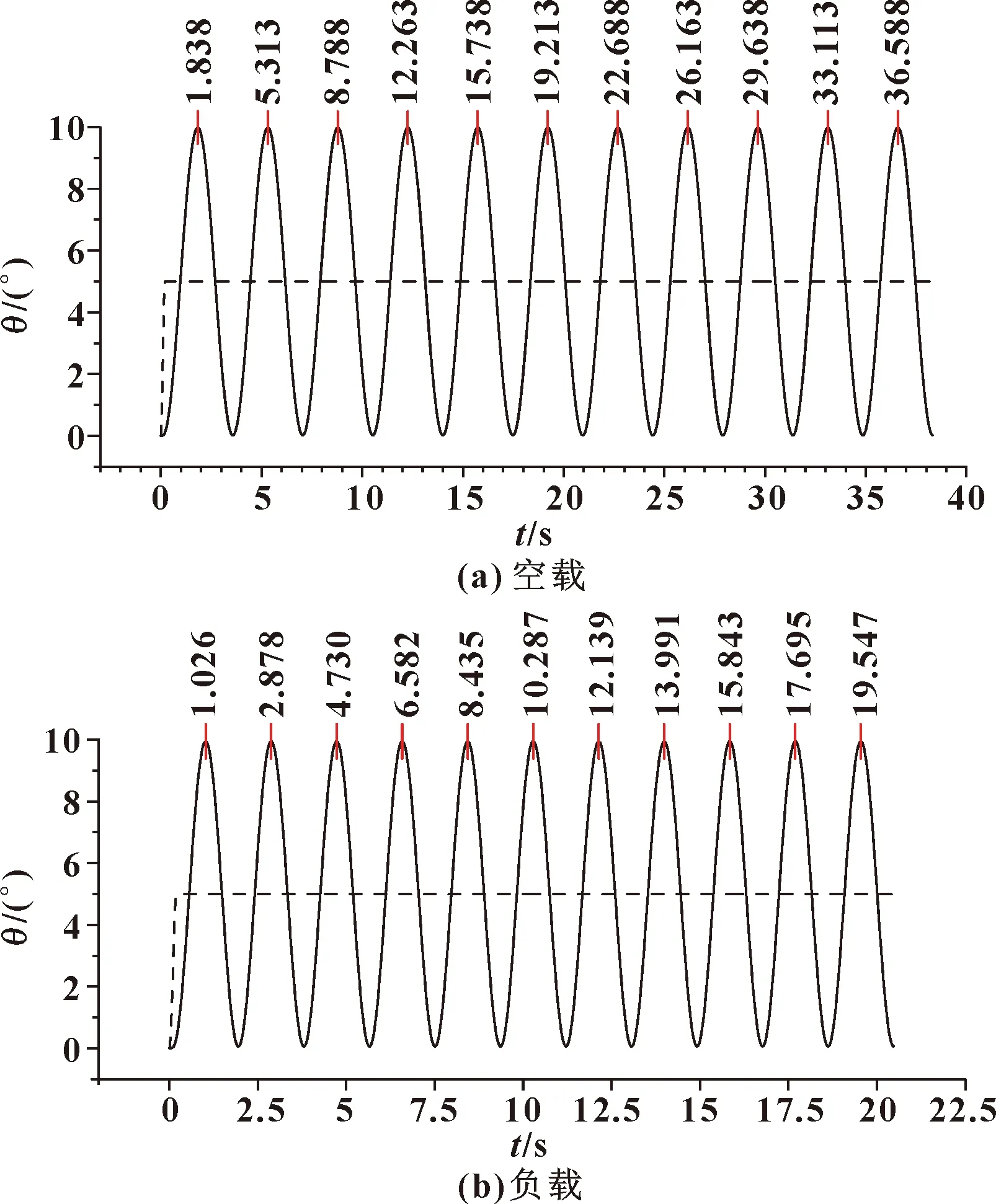
图7 角位移变化曲线(忽略摆线质量)

取前10个周期，通过空载和负载工况下盘角位移的峰值时间，可计算得到和分别为3.475 s和1.852 s，代入公式(11)，有

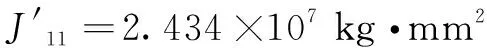
(21)

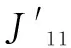
(2)考虑摆线惯性

将Cable参数中的Inertia开关设为on，仿真得到的下盘的角位移-时间曲线见图8。同样地，根据前10个周期的峰值时间，可获得和分别为3.970 s和1.984 s。代入式(11)，得

=2504×10kg·mm

(22)

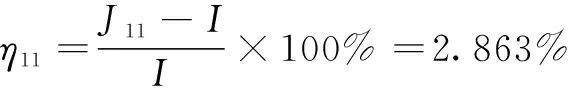
(23)

式中：为在模拟现实工况下根据公式(11)的计算结果；为误差。而将和代入式(20)，已知=1.548 kg，得

=2469×10kg·mm

(24)

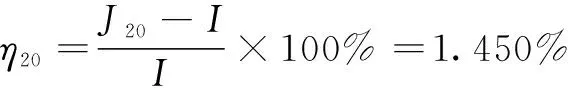
(25)

式中：为改进后根据公式(20)的计算结果；为误差。

结果表明文中提出的改进的三线摆测量方法可有效降低刚体转动惯量的测量误差。

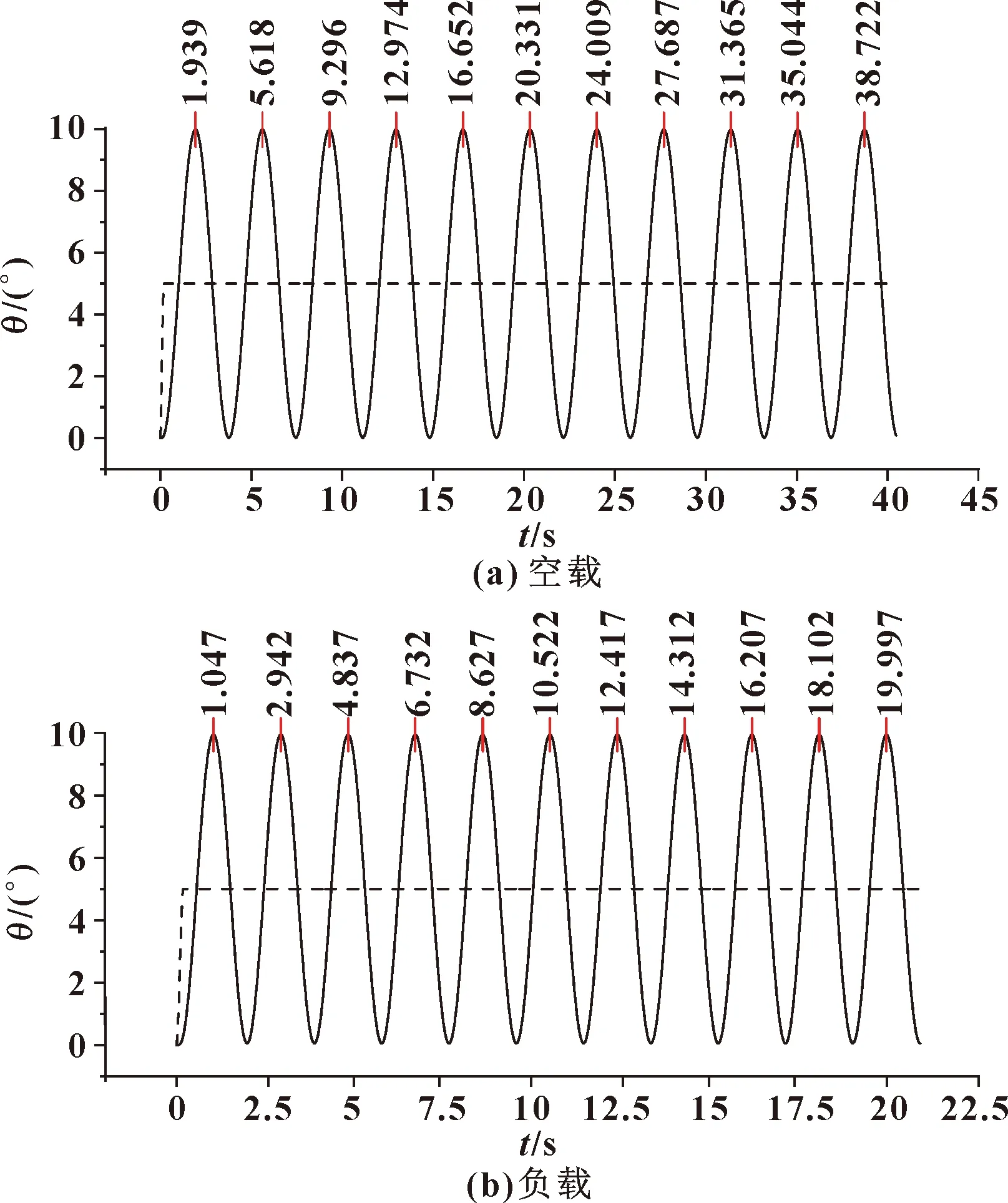
图8 角位移变化曲线(考虑摆线质量)

3 摆线参数影响分析

根据式(19)和(20)可知，若假设摆线直径相同、材质均匀，则对测量结果产生影响的摆线参数包括线密度和长度。下面通过仿真对这两个参数分别进行灵敏度分析虚拟实验。

3.1 线密度ρ

在三线摆虚拟样机模型中，保持摆线长度为6 000 mm，更改材料密度参数，进行多次仿真。下盘和物体总质量约为600 kg，钢丝绳破断拉力需在6 kN以上，由此设置摆线模型的参考质量区间为10～60 kg/100 m，仿真结果见表2。可以看出，改进前、后的测量结果误差与摆线的线密度近似呈线性关系：

=(127157-0003 19)×100

=(63506-0001 35)×100

式中：的单位为kg/mm。

若要提高测量的精度，应在不影响结构安全的情况下尽量选择线密度更小的摆线材料。另外观察到改进后的公式相较于不考虑摆线影响的测量结果误差下降50%左右，即便是该范围内最大线密度60 kg/100 m的钢丝绳，测量误差也从改进前的7.391%下降为3.689%，对精度的提升十分明显。

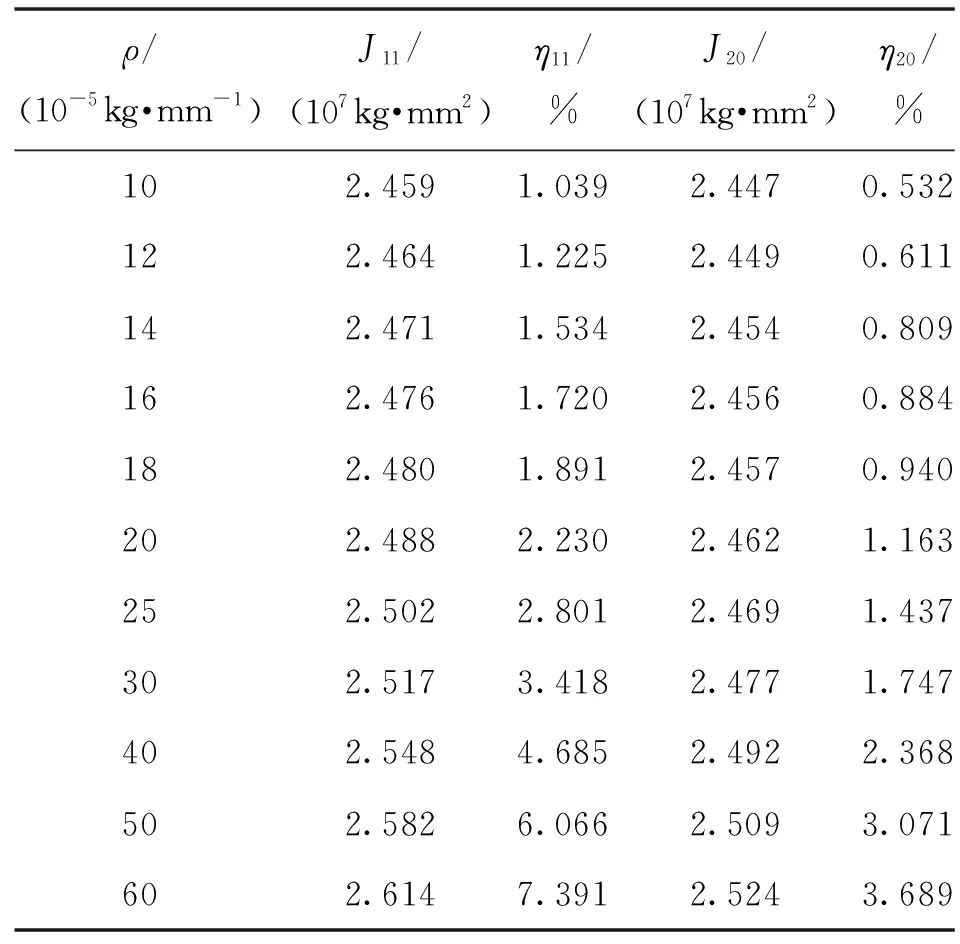
表2 不同ρ值下的仿真结果

3.2 摆线长度L

保持摆线的线密度为25.8×10kg/mm不变，更改摆线长度，进行多次仿真实验。设置摆线长度区间为2 000～8 000 mm，仿真结果见表3。可以看出，在实际测量中，摆线并非越长越好。在≤3 000 mm时，摆线越长，所引起的测量误差越小；超出这个范围，误差随着的增大而增大，但改进后的公式对于误差的降低作用依然明显。针对该模型参数，最佳的摆线长度在3 000 mm附近，分析结果可以指导实验设计。

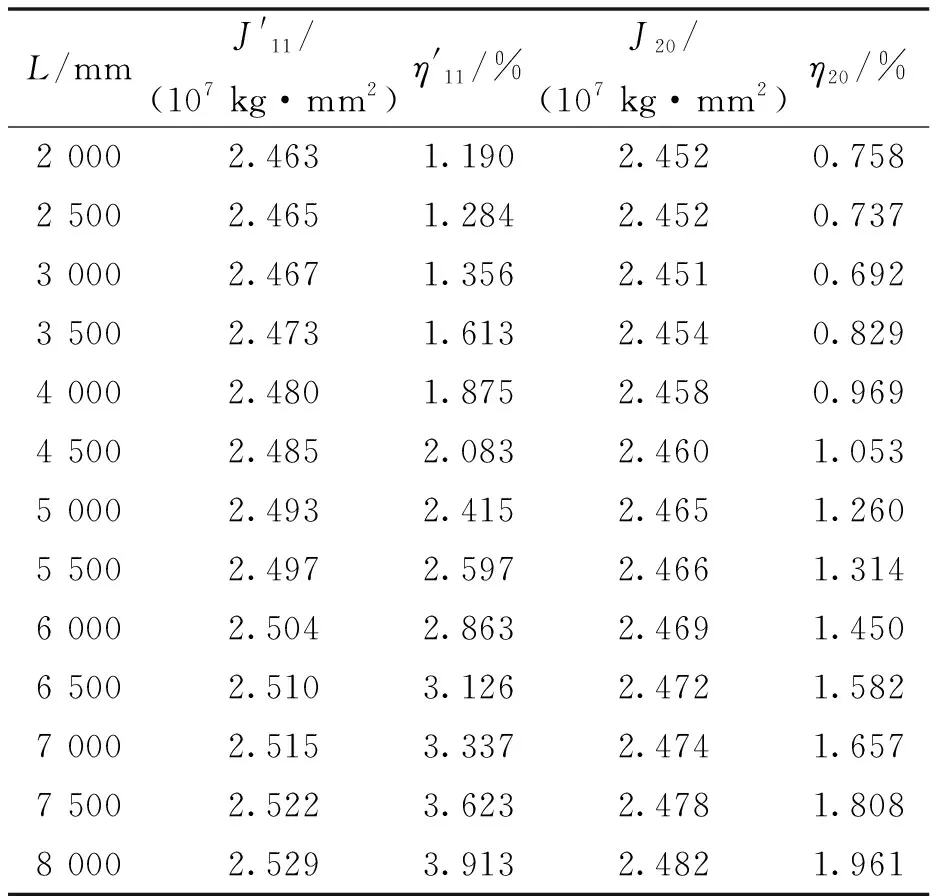
表3 不同L值下的仿真结果

4 结论

基于能量守恒定律推导了考虑摆线质量参数时的三线摆刚体转动惯量计算方法。在ADAMS/View中建立了测量大质量物体转动惯量的三线摆虚拟样机测试模型，通过虚拟实验验证三线摆计算方法的正确性，并揭示了摆线线密度和长度对测量精度的影响规律。整体上，改进后的计算方法比不考虑摆线影响的测量结果误差约降低50%左右。为了提高三线摆法测量精度，可在许可范围内尽可能选取较小的摆线密度和最优的摆线长度，文中方法可指导实验平台设计。