基于进给优化的五轴机床高精度加工研究

王炳达

(沈阳工程学院机械学院，辽宁沈阳 110136)

0 前言

五轴数控(CNC)机床已广泛用于加工具有复杂雕刻表面的零件，如模具和航空航天零件。在高速五轴加工应用中，保持所需的尺寸精度是普遍面临的挑战。在五轴加工过程中，零件的尺寸精度主要受进给驱动跟踪系统和对应的刀具定位误差的影响。伺服系统须具有高闭环带宽，以便准确跟踪快速变化的参考工具位置命令。此外，由于五轴机床是耦合非线性运动学，驱动器的小定位误差可能导致刀尖过度偏离所需轨迹。因此，集中控制器的设计可以解决轴之间的协调，以实现所需的轮廓精度。同样，参考刀具轨迹须是平滑的，以避免激发驱动系统的结构动力学，从而避免超出轴伺服带宽的运动指令引起的过渡轮廓误差。平滑时间最优轨迹生成和精确运动控制是本文作者研究五轴加工过程中实现轮廓精度的两个重要组成部分。

用于五轴加工的轮廓刀具路径由计算机辅助设计/制造(CAD/CAM)系统以非均匀有理B样条(NURBS)格式生成，可通过现代CNC系统进行处理。虽然在NC程序段中指定了恒定进给，但所有5个驱动器上的速度、加速度和加加速度可能会随着路径曲率和机床的反向运动而连续变化。当每个驱动器的速度、加速度和加加速度超过其物理饱和极限时，则违反伺服控制的线性操作，导致表面上的严重划痕或控制器不稳定。因此，需要研究在不违反机器驱动器物理限制的情况下，在最短的时间内生成穿过样条刀具路径的平滑轨迹。

很多研究者已经针对样条刀具路径的笛卡尔加工提出了一些方法。部分学者使用加速度限制来生成速度限制曲线，并采用了与SHILLER和LU类似的方法，在笛卡尔坐标系下沿刀具样条曲线找到最佳进给率。RENTON和ELBESTAWI提出了一种计算效率高的两轮算法来解决最小时间馈送优化问题，该算法通过在正向和反向扫描轨迹来进行，缺点是：生成的轨迹具有不连续的加速度，违背了使用平滑刀具路径的基本目的，并导致高速加工中的轮廓不准确。

为了提高跟踪性能，驱动器的加加速度限制被视为以增加计算复杂度为代价的约束。这些方法需要迭代解决方案，而不是最佳控制公式。例如，CONSTANTINESCU和CROFT使用扭矩率约束并迭代优化样条轨迹以实现机械手的最短时间运动。加加速度限制轨迹也适用于机床，并且其计算效率高，一直受到CNC实时控制的青睐。ALTINTAS和ERKORKMAZ后来将位移曲线定义为沿刀具路径的最小加加速度五次样条曲线，并迭代优化每段的行程时间；同时考虑了驱动器的速度、加速度和加加速度限制，以实现更平稳的运动。尽管他们的方法可以扩展到任何类型的多轴机床，但要考虑约束数量会随着轴数的增加而急剧增加。

文献[8]提出了第一个交叉耦合控制算法，以减少刀尖与路径的法线偏差。CHIU和TOMIZUKA开发了一种轮廓误差估计程序，用于连续弯曲刀具路径的两轴加工，可预估笛卡尔轴在刀具路径切线和法线方向上的跟踪误差，并将法线方向上的误差分量作为实际轮廓误差的近似值。因此，这种方法还能够估计样条曲线和其他曲线的轮廓误差。如果切线方向的误差很大，则轮廓误差近似变得不准确，尤其在具有高曲率的路径高速加工工况。除了笛卡尔轮廓系统，姜辉等人解决了非正交可重构三轴机床的轮廓问题，他们模拟了机床的运动学，并为Equa设计了随时间变化的增益。

本文作者介绍一种加加速度连续进给优化技术，以最大限度减少五轴加工中的循环时间，同时保证沿样条刀具路径行进的运动平滑度和跟踪精度，为五轴加工的进给率优化技术提供参考。

1 五轴机床轮廓误差建模

图1为高速五轴机床加工示意，由于伺服控制器的动态特性，机床上的每个驱动器都会在命令位置和实际位置之间产生不可避免的跟踪误差。这些跟踪误差通过运动学原理转换到刀尖，导致指令刀具路径和CNC单元提供的实际路径之间产生轮廓误差。在实践中，每个驱动器的专用控制法最小化单个轴跟踪误差、、。由于五轴机床的非线性，旋转轴上的微小跟踪误差可能导致刀尖相对于工件的参考刀具路径偏差较大。此外，当一个轴受到干扰时，其他轴仍然执行正常工作，这会导致整体轮廓精度产生变化。

图1 高速五轴机床加工示意

轮廓误差定义为与所需刀具路径的正交偏差，是零件精度的实际度量。图2说明了简单线性和曲线刀具路径的轮廓误差和轴跟踪误差之间的关系。当遵循线性刀具路径时[图2(a)]，轮廓误差可以表示为轴跟踪误差的简单分析函数、，如：

=-+

=sin

=cos

(1)

式中：为笛卡尔坐标下的轮廓误差；为方向的增益；为方向的增益；为角度的变化。

另一方面，在加工如B样条或NURBS之类的弯曲路径时，精确计算轮廓误差变得更具挑战性[图2(b)]。使用公式(1)来估算沿简单线性刀具路径的两轴加工轮廓误差。

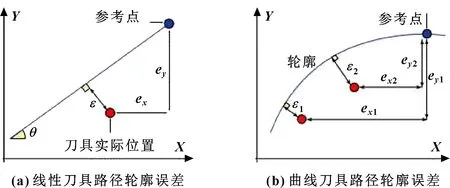
图2 两轴笛卡尔加工中轮廓误差的定义

2 最短时间进给优化

在不违反5个驱动器的速度、加速度和加加速度限制的情况下沿刀具路径进给。计算给出的轴约束叠加为

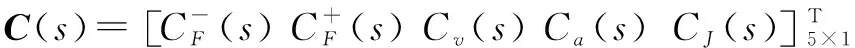
(2)

其中确保向前运动的速度下限(即进给方向)是用户的上限。进给曲线以B样条形式表示，并通过最大化控制点定义进给量来优化加工时间：

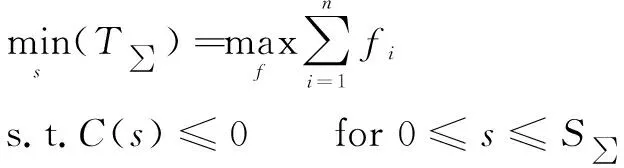
(3)

由于关于时间的二阶导数为零，求解方程是具有非线性约束的线性规划问题，产生一个序列二次问题(SQP)，并使用MATLAB的优化工具箱求解。

沿刀具路径进给优化曲线如图3所示。随着进给曲线的迭代改变，获得了一组可行的控制点，该控制点不违反约束并且最小化整个循环时间。

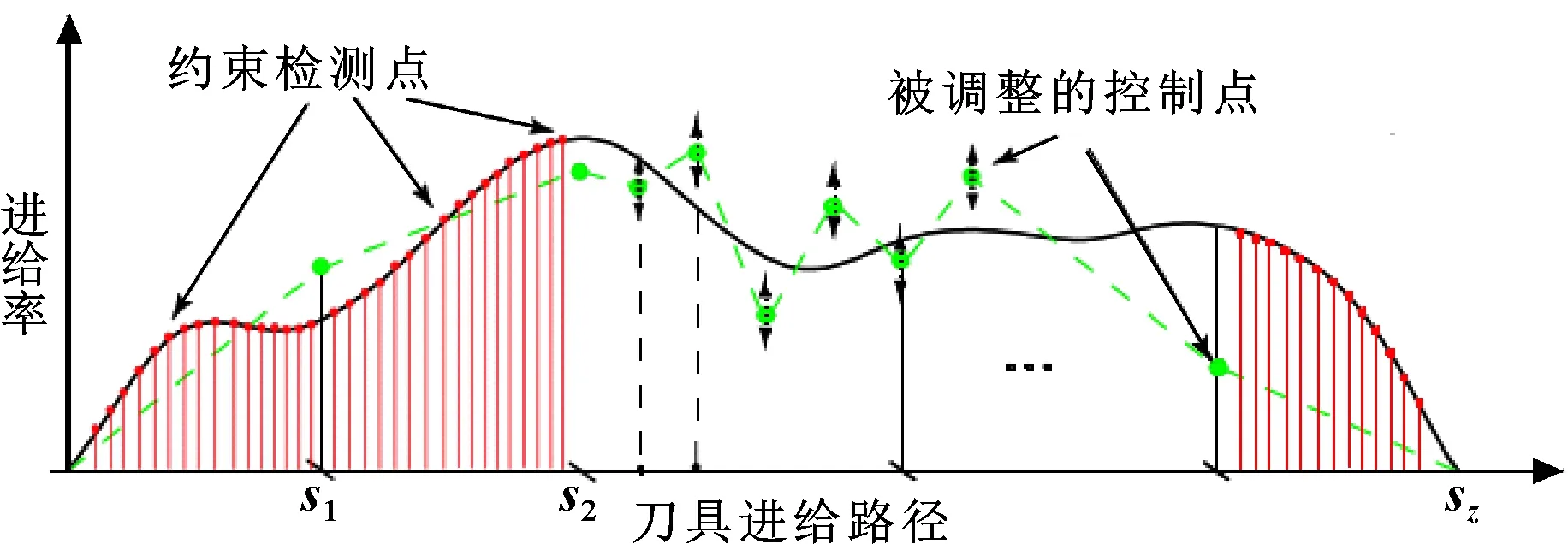
图3 沿刀具路径进给优化

如果沿整个刀具路径同时考虑所有进给控制点，则优化过程的计算效率很低，因为需要考虑大量优化变量和约束。相反，优化算法应用移动窗口技术，考虑每个窗口上一组较少的控制点，如图4所示。

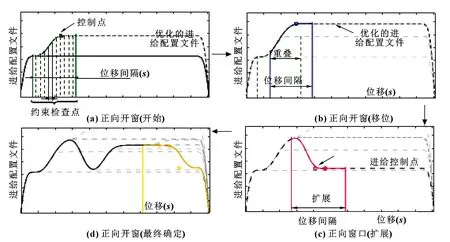
图4 开窗技术

收敛后，窗口沿刀具路径移动，如果特定窗口中的轨迹优化没有收敛到可行的轮廓，则通过扩大窗口大小来回溯解决方案。当刀具路径末端的最终进给率设置为0，以要求机床完全停止。在这种情况下，通过从之前的窗口控制点来扩展最后一个窗口，直到获得可行的制动距离。

3 试验结果

在开放式结构的五轴机床上测试文中提出的轨迹优化方法。该机床具备倾斜旋转工作台运动学轨迹。图5所示为用于喷射叶轮的五轴侧面铣削测试刀具的设计路径。包含196个离散数据点的刀具路径被拟合到五次B样条中，刀尖弦误差为35 μm，方向误差限制在0.09°以下。沿刀具路径的曲率不断变化，但最高曲率位于起点(25～50 mm)、中间(150～190 mm)和接近末端(250～290 mm)，工具必须在刀片的后缘和前缘周围移动。沿300 mm长刀具路径的相应轴位置如图6所示。在CL文件中，介绍了实验性五轴机床设置，刀具路径的编程进给速度为150 mm/s。轴运动学限制在表1中给出，驱动系统由具有前馈摩擦补偿的控制器控制。

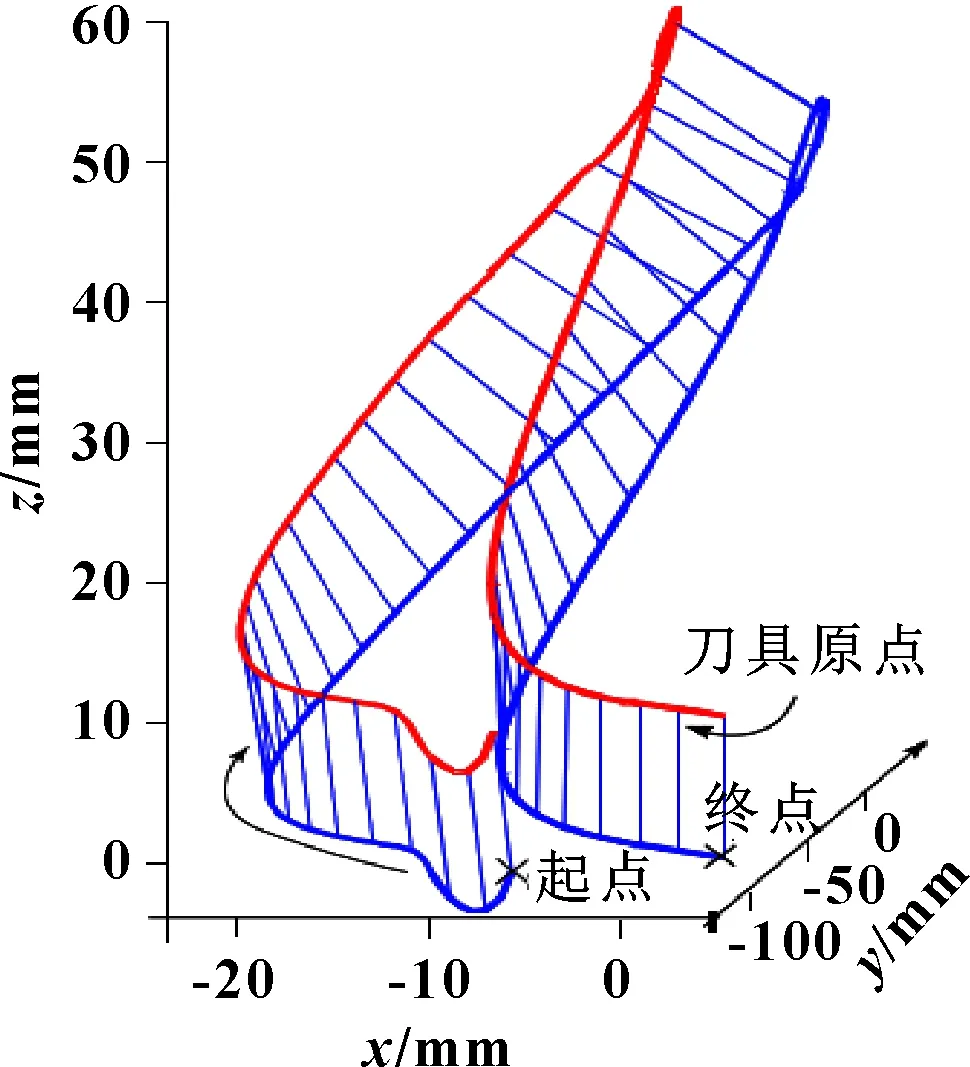
图5 五轴刀具路径

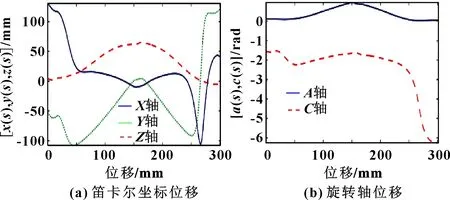
图6 轴参考位移

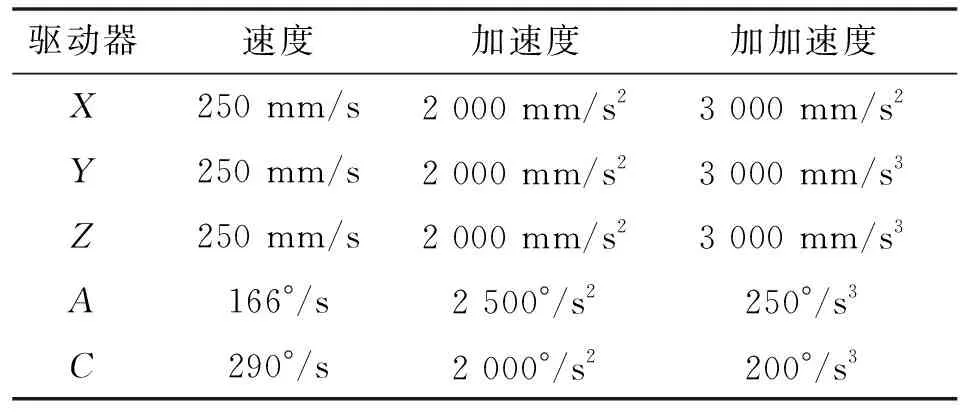
表1 进给优化采用的驱动限制

受驱动速度、加速度和加加速度限制约束的进给速度如图7所示。根据路径的曲率，不同的驱动器会限制沿刀具路径的进给速度。如在路径位置=34 mm，轴将最大进给速度限制在58 mm/s和驱动器在路径位置限制进给速度为267 mm/s。类似地，驱动器的加速度和加加速度在不同位置限制进给速度。通过沿路径最小进给评估速度(图7(a))、加速度(图7(b))和加加速度(图7(c))的限制，包络线可以作为沿刀具路径选择进给速度的指南。然而，不可能完全将由最慢包络曲线定义的进给率作为最佳速度曲线来实施。由于沿包络线的任意两点之间的速度变化可能会违反驱动器的加速度或加加速度限制，因此必须通过同时优化所有5个驱动器的速度、加速度和加加速度限制来评估最佳进给。由图7可知：切向进给的加速度和加加速度限制相比于速度限制较密集，限制区域也较多，轴速度限制较容易满足。当工艺设计者设置进给速度限制为150 mm/s，沿路径生成的进给进度如图8所示。

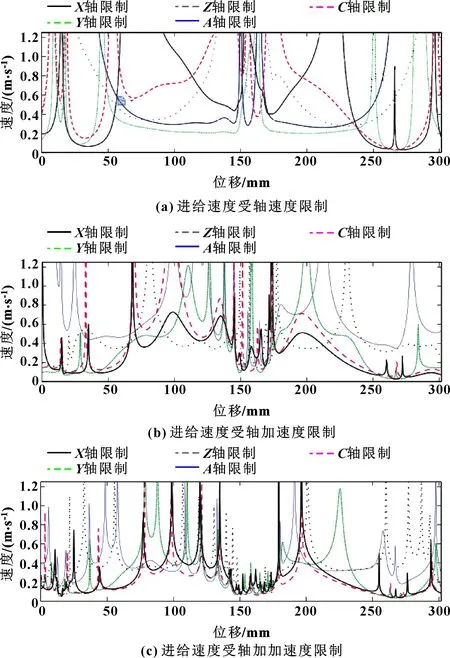
图7 切向进给上的轴限制

可以看出，如果机器以150 mm/s的速度运行，则在路径区域(0～60 mm、140～165 mm、240～300 mm)会违反驱动限制，其中叶轮叶片曲率较高。如果进给保持恒定在15 mm/s，则不会超出任何驱动限制，但加工时间变为=20.18 s。当通过将B样条拟合到=276沿工具均匀分布的点来优化进给路径，加工时间下降到=4.664 s，导致生产率增加80%。该算法可在MATLAB环境中2.3 GHz CPU速度的P4计算机上用时126 s求解。如图8所示，计划进给已经在实验性五轴机器上进行了测试，每个驱动器上的速度、加速度和加加速度都没有超出它们的限制。此外，根据五轴刀具路径的复杂性，已统计出解决优化问题的不同计算时间，优化后的加工时间明显小于优化前的加工时间，加加速度曲线优化后的摆幅较大，由图9可知优化前和优化后其结果都没有违反算法中施加的限制。

图8 优化和未优化的进给配置文件

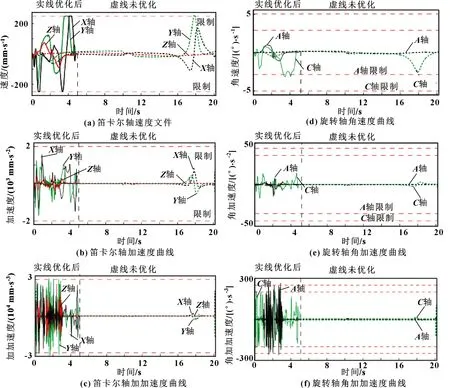
图9 优化和未优化的轴轮廓

除了减少加工时间，所提出的优化措施还提高了驱动器未饱和时机器的跟踪精度。图10显示了3种情况下的实验测量跟踪误差。当进给速度设置为最保守的速度(15 mm/s)时，加工永远不会违反驱动限制，由于速度慢，跟踪精度最好，但加工时间变为=20.18 s；如果使用了强制进给 150 mm/s，驱动器将变得过度饱和，机器将变得无法控制。布尔测试了相对保守进给40 mm/s时，导致违反驱动限制(图10)，跟踪误差在沿路径的饱和区域。然而，当进给优化时，机器能够在大多数位置达到150 mm/s所需的进给，并且未违反驱动限制。机床控制保持在线性控制区域内，跟踪精度与速度成线性比例，与驱动器的带宽成反比。由图10可知：轴和轴的跟踪轨迹误差相对于、、轴较平稳。

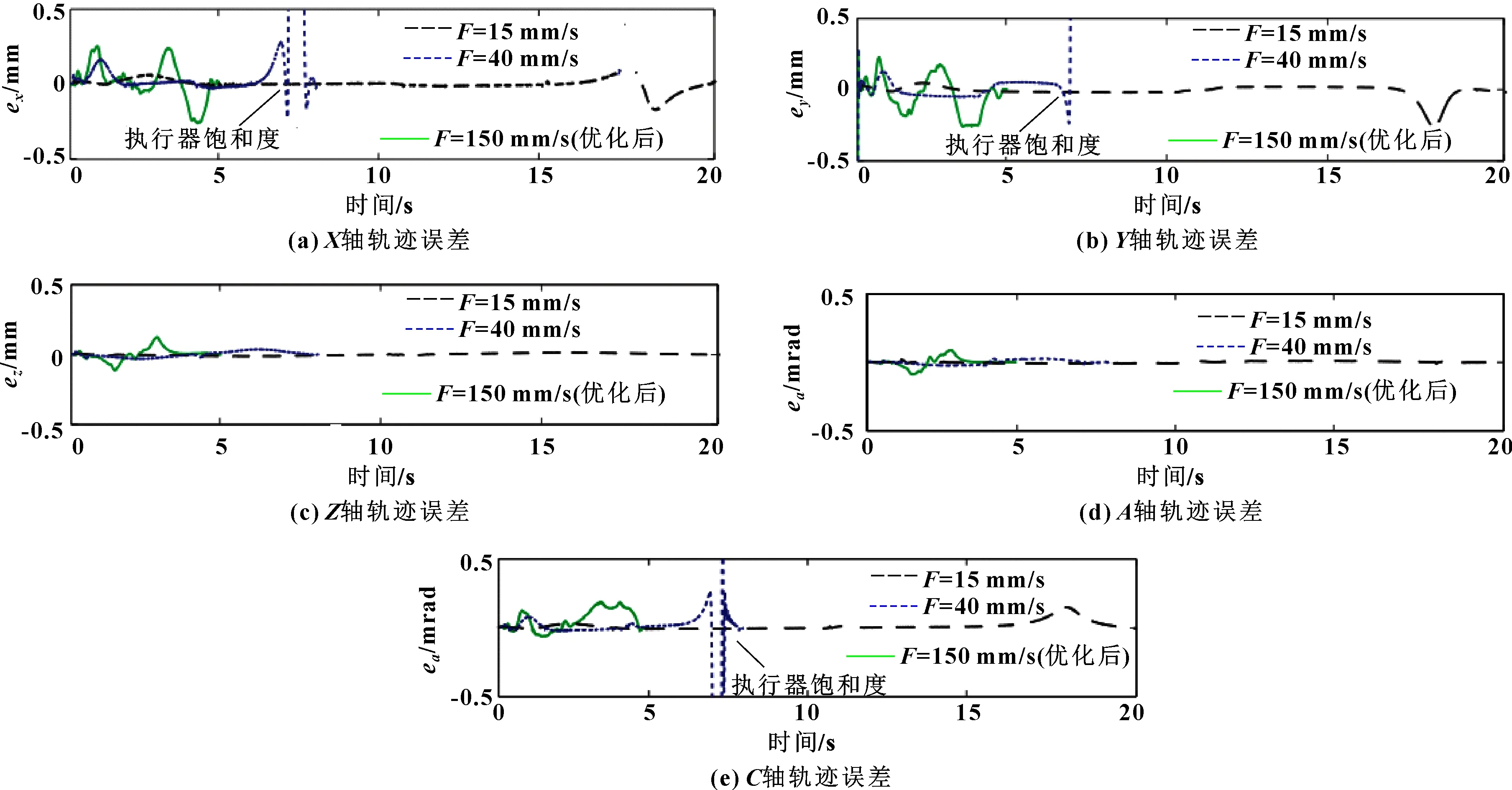
图10 轴的跟踪轨迹误差

4 结论

金属切削过程、机床的结构动力学、机器的精度以及驱动器的运动学和控制制约了零件的五轴加工生产率。开发一种算法，在所有5个驱动器的速度、加速度和加加速度限制内能显著优化沿刀具路径的进给速度，从而缩短加工时间。此外，通过避免违反驱动器的饱和限制，控制器可以在线性区域内运行，从而提高CNC系统的精度和性能。在五轴侧面铣削时，当轴向切深较长时，沿刀具轴线的切向进给速度会发生变化，从而导致每个驱动器的速度、加速度和加加速度参数相互冲突。此算法可以通过考虑该位置沿刀具轴线重复的切向进给速度，选择满足驱动约束的进给速度。