插装式二维电液伺服阀的动态特性研究
2022-10-25丰章俊
丰章俊
(浙江同济科技职业学院机电工程学院,浙江杭州 311231)
0 前言
电液伺服阀是电液伺服系统中的核心部件,高功重比是它显著的优势与特点之一。伺服阀的插装化设计是提升其功重比的重要手段,能够摒弃传统伺服阀沉重的阀套,保留伺服阀的优良性能,同时还具有成本低、无泄漏、流量大等特点,广泛应用于工业和移动机械领域。二维伺服阀凭借其独有的伺服螺旋机构,易于实现伺服阀的插装化设计。已提出了多种插装式二维伺服阀,并成功投入使用。
为研究一款插装式二维电液伺服阀(以下简称“插装式二维阀”)的动态特性,建立其数学模型,运用解析求解的方法求得旋转总成黏性系数,通过仿真分析不同系统压力下插装式二维阀开、闭环时的动态特性,最后通过试验验证所建立数学模型的正确性。
1 插装式二维电液伺服阀的结构及工作原理
1.1 结构原理
插装式二维电液伺服阀的结构及工作原理如图1所示,主要包括力矩马达模块及二维阀模块。力矩马达模块包括永磁体、极靴、衔铁、励磁线圈以及霍尔传感器。其中,永磁体分布在力矩马达的两侧,衔铁由2个励磁线圈包围,霍尔元件安装在连接板上,以实现二维阀的位置闭环控制。二维阀部分包括二维阀芯、阀套,二维阀芯与衔铁固连。阀套上设有A、B、P、T 4个阀口,其中A、B为工作油口,P为进油口,T为回油口。二维阀芯上设有高压槽、低压槽,低压槽与T口直接相通,高压槽与P口沟通。二维阀芯与阀套配合在图中右侧形成敏感腔,左侧形成了高压腔,高压腔通过高压槽与P口沟通。二维阀芯上的高、低压槽与阀套上的斜槽形成的重叠面积决定了敏感腔内的油液压力。
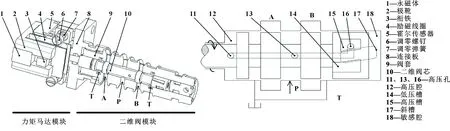
图1 插装式二维电液伺服阀的结构及工作原理
1.2 工作原理
插装式二维阀的力矩马达模块用于输出旋转力矩,驱动与衔铁固连的二维阀芯旋转,二维阀模块则是将力矩马达模块中衔铁的旋转转换为阀芯直动,实现阀口开闭。如图 1所示,高、低压槽分布在斜槽的两侧,形成了两平行四边形重叠面积,构成了液压半桥。液压半桥的入口压力为系统压力,出口为回油口压力,中间可变压力即为敏感腔压力。
当力矩马达无力矩输出时,二维阀芯不会转动,两平行四边形重叠面积大小相等。液压半桥的输出压力(即敏感腔压力)为系统压力(即高压腔压力)的一半;在结构设计时,高压腔的作用面积为敏感腔作用面积的一半,故此时二维阀芯处于受力平衡状态。
当力矩马达输出力矩时,二维阀芯会旋转,此时两平行四边形重叠面积不再相等,敏感腔压力发生变化,导致敏感腔与高压腔内的压力出现液压力差,二维阀芯轴向受力失衡,阀芯轴向移动。二维阀芯的移动会使两重叠面积回到相等的状态,即二维阀芯的轴向液压力差会不断减小,最终恢复到平衡状态。
2 插装式二维伺服阀的数学模型
插装式二维阀具有轴向移动与周向旋转2个运动自由度,对这两类运动分别建模。
2.1 周向旋转过程的数学模型
力矩马达的输出力矩将驱动二维阀芯-衔铁组件旋转,力矩马达的力矩方程为
=+
(1)

(2)
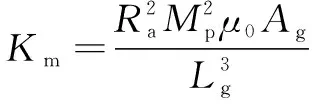
(3)
式中:为力矩马达的输出力矩;为力矩马达的中位电磁力矩系数;为线圈电流;为力矩马达的中位电磁弹簧刚度;为衔铁的转动角度;为衔铁的转动半径;为永磁体产生的极化磁动势;为空气的磁导率;为气隙的有效工作面积;为气隙的初始长度;为线圈匝数。和的表达式已在参考文献[10]中有详细推导,不再赘述。
二维阀芯-衔铁组件的运动学方程为

(4)
式中:为二维阀芯-衔铁组件的转动惯量;为旋转黏性阻尼系数;为二维阀芯-衔铁组件的扭转弹簧刚度;为任意外部负载力矩。
旋转运动过程的传递函数框图可通过式(1)—式(4)得到,如图2所示。
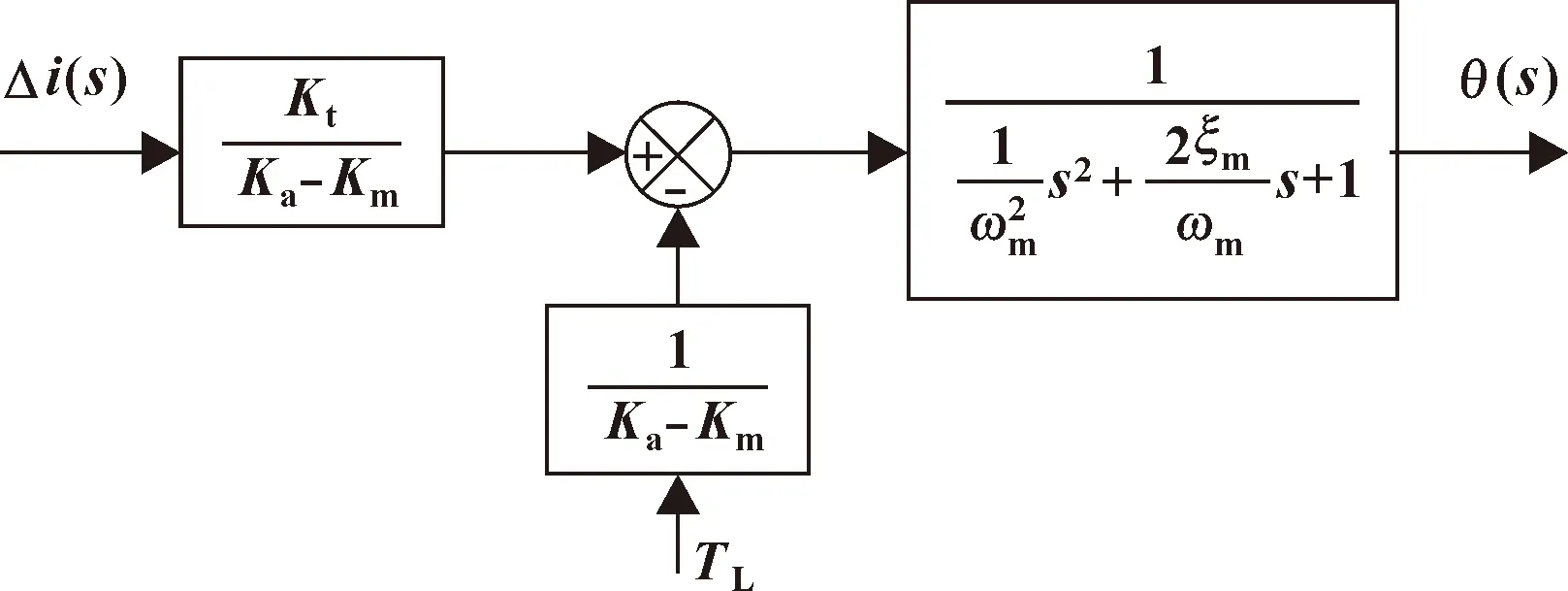
图2 旋转运动的传递函数框图
根据图 2可以推导得到如式(5)所示的旋转过程的传递函数:
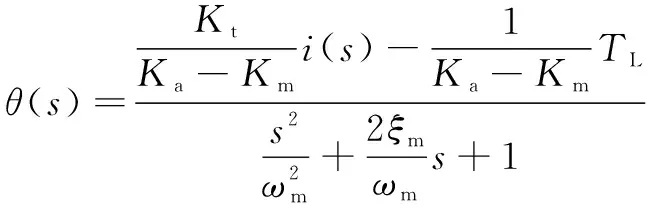
(5)

(6)
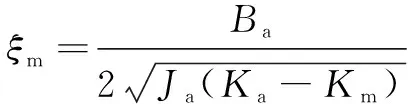
(7)
式中:为力矩马达的固有频率;为力矩马达的阻尼比。
2.2 旋转总成黏性阻尼系数的分析
旋转总成黏性阻尼系数由两部分组成:其一为旋转剪切流动产生的摩擦黏性阻尼系数,其二为二维阀芯端部内瞬态液动力矩造成的旋转黏性阻尼系数。
2.2.1 摩擦黏性阻尼系数的计算
如图3所示,当二维阀芯与阀套发生相对转动时,二者间的间隙会产生旋转剪切流动。由于间隙长度要远小于二维阀芯的端部直径,故此流动可视作平行流动。

图3 旋转剪切流动示意
摩擦力矩表达式为

(8)
因此摩擦黏性阻尼系数为

(9)
式中:为油液的动力黏度;为二维阀芯的直径;为间隙长度;为旋转剪切流动的有效长度。
2.2.2 旋转黏性阻尼系数的分析
二维阀芯的旋转使高、低压槽与斜槽间的油液流量交换发生变化,会在二维阀芯上产生瞬态液动力矩。根据设计要求,二维阀芯的单边极限旋转角度为1°(以顺时针转动为正方向)。按插装式二维阀芯的工作原理对瞬态液动力矩分段进行分析。首先考虑高压槽与斜槽间的瞬态液动力矩,如图4所示。

图4 高压槽与斜槽间瞬态液动力矩示意
根据插装式二维阀的工作原理,从高压槽流至斜槽的流量为

(10)
式中:为流量系数;为高压槽与斜槽的重叠面积;为油液的密度;为系统压力;为敏感腔压力。
高压槽与斜槽的重叠面积可表示为
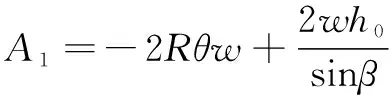
(11)
式中:为二维阀芯的半径;为高压槽的宽度;为二维阀芯的旋转角度;为高压槽与低压槽的初始重叠高度;为斜槽的角度。
根据瞬态液动力的定义,有

(12)
式中:为高压槽与斜槽的阻尼长度。
从式(10)—式(12)可知:高压槽与斜槽间的瞬态液动力矩可表达为
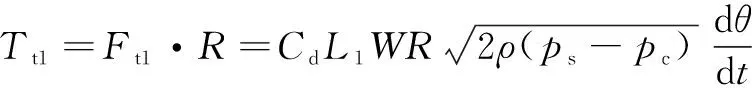
(13)
式中:为高压槽与斜槽重叠面积的面积梯度。
图 4(a)与图 4(b)中的阻尼长度大小相等,方向相反,现设图 4(a)所示瞬态液动力矩为正。故高压槽与斜槽间产生的旋转黏性阻尼系数为
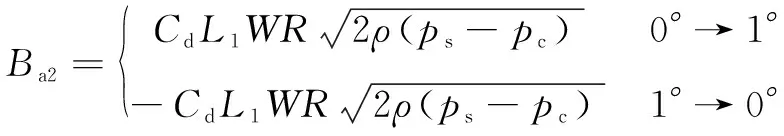
(14)
图5所示为低压槽与斜槽间的瞬态液动力矩。
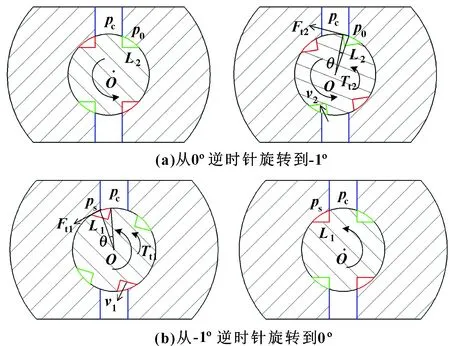
图5 低压槽与斜槽间瞬态液动力矩示意
类似的,从斜槽流入低压槽的流量为

(15)
式中:为低压槽与斜槽重叠面积的面积梯度。
低压槽与斜槽的重叠面积可表示为
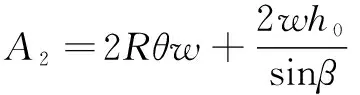
(16)
低压槽与斜槽间的瞬态液动力矩可表示为

(17)
式中:为低压槽与斜槽的阻尼长度。
图5中的阻尼长度情况与图 4类似,其中图 5(b)中为正值。因此可得:

(18)
联立式(9)(14)(18),旋转总成黏性阻尼系数可表示为
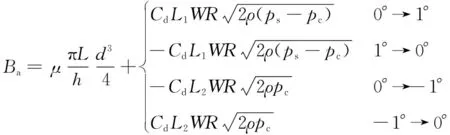
(19)
2.3 轴向移动的数学模型
基于插装式二维阀的工作原理以及流量连续性公式,可得敏感腔内的流量为
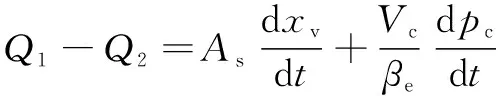
(20)
式中:为敏感腔的工作面积;为二维阀芯的轴向位移;为敏感腔的体积;为油液的体积弹性模量。
二维阀芯-衔铁组件的运动方程为

(21)
式中:为高压腔工作面积;为二维阀芯-衔铁组件的质量;为轴向黏性阻尼系数;为二维阀芯-衔铁组件的轴向弹簧刚度;为任意负载力。
二维活塞的轴向移动与周向转动之间的具体关系可通过结合考虑二维活塞转动与轴向移动时高、低压槽与斜槽的重叠高度变化量Δ的表达式来表达
Δ=sin-cos
(22)
根据式(20)—式(22),轴向运动的传递函数框图可表示为图6。

图6 轴向运动的传递函数框图
根据参数的实际值可有:
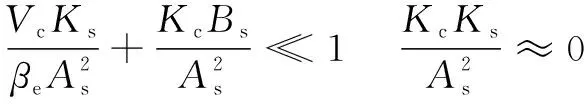
(23)
由于油液体积弹性模量的数量级很大,导致液压固有频率要远大于插装式二维阀的工作频宽,因此图 6中所含的闭环传递函数可简化写为

(24)
式中:为流量增益。
2.4 插装式二维电液伺服阀的数学模型
插装式二维阀处于开环控制时,由式(1)—式(24)可得开环传递函数及对应框图如图7所示。

图7 插装式二维伺服阀的开环传递函数框图

(25)
插装式二维阀处于闭环控制时,控制器中的PID算法会提升控制精度与二维阀的响应速度。PID算法的表达式为

(26)
式中:为比例系数;为积分时间常数;为微分系数;为过滤系数。
因此闭环传递函数及对应框图可表示为式(27)及图8。
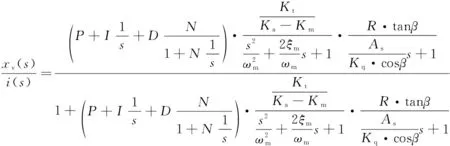
(27)

图8 插装式二维伺服阀的闭环传递函数框图
3 仿真分析
通过Simulink模块对插装式二维伺服阀的开闭环传递函数进行了仿真,主要参数如表1所示,其中—为开环传递函数的PID参数,—为闭环传递函数的PID参数。
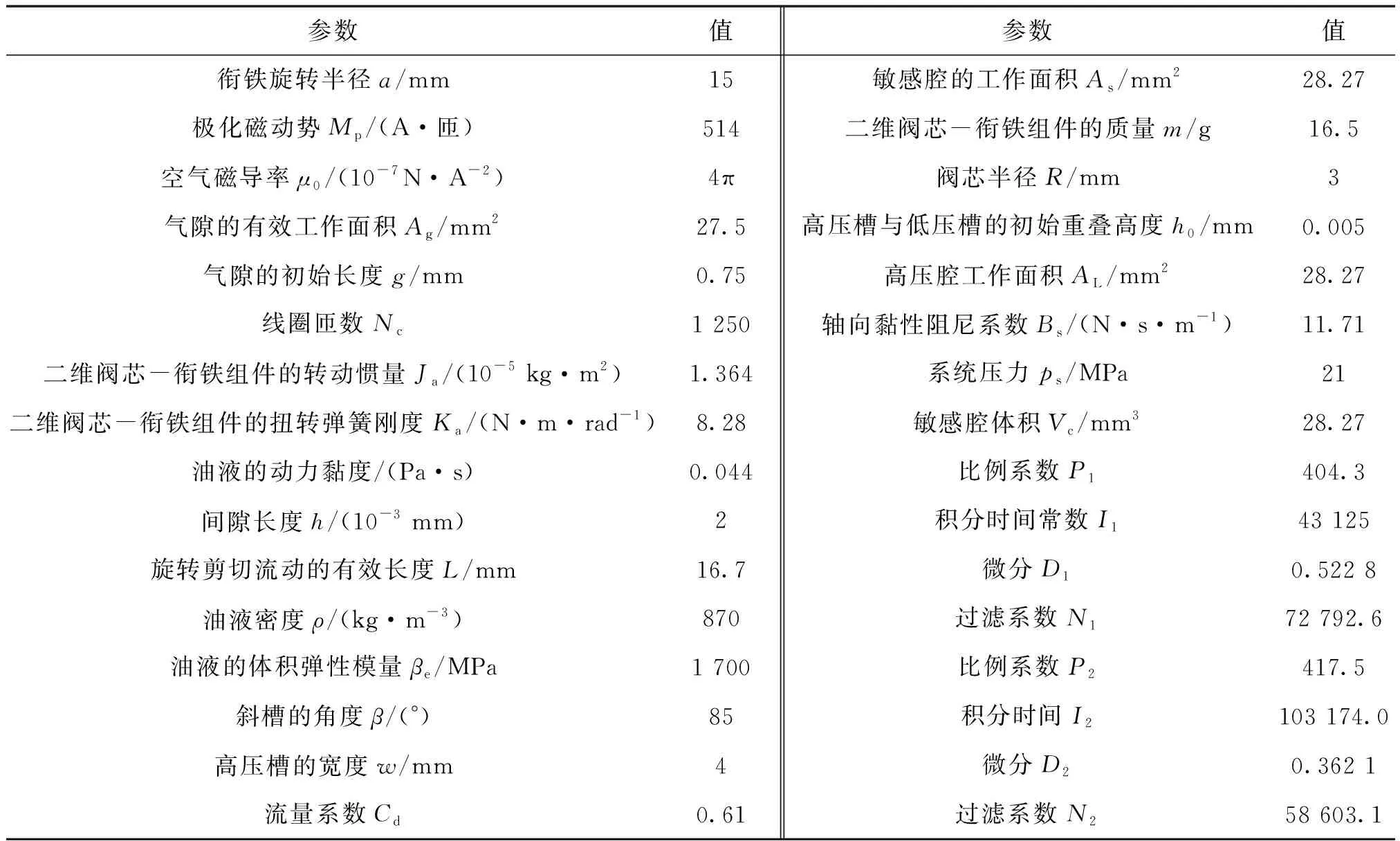
表1 插装式二维伺服阀的主要参数
系统压力对于插装式二维阀阶跃响应特性的影响如图9所示。在不同系统压力下,阶跃响应曲线始终为过阻尼状态,模型的上升时间基本不变,开环时为10 ms,闭环时为4 ms。

图9 系统压力对于开、闭环传递函数阶跃响应特性的影响
图10所示为不同系统压力下2个数学模型的频响特性仿真。图 10(a)显示:随系统压力上升,开环模型的频响特性曲线几乎没有变化,其幅频宽为40 Hz,相频宽为70 Hz。由图 10(b)可知:系统压力为21 MPa时,闭环模型的幅频宽为100 Hz,相频宽为200 Hz。与开环模型不同,当系统压力不断增大时,模型的相频宽从160 Hz增加到了200 Hz,而幅频宽几乎没变。

图10 系统压力对于开、闭环模型频响特性的影响
4 试验模型及试验研究
4.1 试验模型
图11为试验样机与动态特性试验台,试验台包括泵站、信号发生器、示波器、试验样机、控制器和压力表等。泵站提供最高21 MPa的系统压力。压力表检测A、B、P、T的压力。控制器提供PID算法,实现伺服阀的闭环控制。信号发生器产生不同波形的输入信号,输入信号及二维阀芯的轴向位移的曲线会在示波器上显示。

图11 插装式二维电液伺服阀试验台
4.2 试验研究
图12所示为开环控制下仿真与试验结果的对比。从图 12(a)可以看出:试验曲线的上升时间为7 ms左右,且无超调,仅有一些振荡。这可能是二维阀芯的转动角度对霍尔传感器的测量造成了影响。图 12(b)显示试验样机的幅频宽为38 Hz,相频宽为70 Hz。

图12 开环模式下试验与仿真曲线对比
图13所示为闭环模式下仿真与试验结果的对比。图 13(a)显示试验样机的阶跃响应时间为6 ms,而仿真曲线为4 ms,试验曲线中存在一些振荡,这是PID的调节作用产生的影响。图13(b)中的曲线表明样机的幅频宽为117 Hz,相频宽为180 Hz,试验曲线与仿真曲线在低频部分有些差别这可能是由于推导数学模型时忽略了磁漏、磁滞等因素的影响导致。

图13 闭环模式下试验与仿真曲线对比
4.3 试验结果
系统压力21 MPa、25%输入信号时,插装式二维阀与MOOG D662-P的闭环动态特性如表2所示,可见这两款伺服阀的动态性能较为接近,插装式二维伺服阀在一些参数上略有优势。
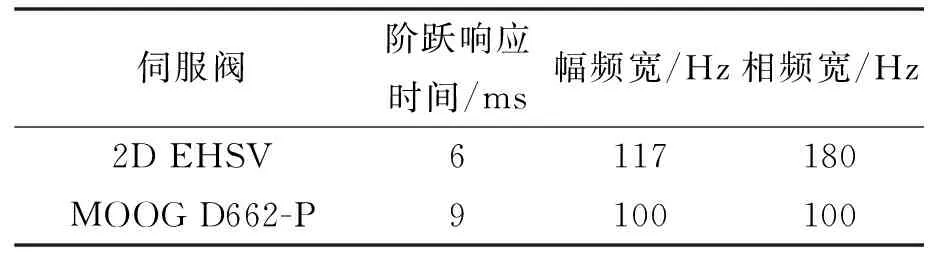
表2 两款伺服阀的动态性能参数
5 结论
(1)推导并建立了开环与闭环2种模式下插装式二维阀的数学模型并进行仿真分析。区别传统所用的系统辨识方法,对旋转黏性阻尼系数进行了解析分析。仿真结果表明闭环时插装式二维阀具有更好的动态特性,且系统压力对于插装式二维阀动态特性的影响很小。
(2)制造试验样机并进行了动态特性试验。阶跃响应特性试验结果显示,开环时样机的阶跃响应时间为7 ms,闭环时为6 ms。试验与仿真结果基本一致,但开、闭环试验曲线存在一些振荡。开环曲线的振荡可能是二维阀芯的位置反馈或者是轴向阻尼系数过小导致的,而闭环曲线中的振荡可能是PID算法的位置反馈调节造成的。
(3)频响特性试验中,开环时样机幅频宽为38 Hz,相频宽为70 Hz,闭环时幅频宽为117 Hz,相频宽为180 Hz。闭环情况下试验与仿真曲线在低频部分存在一些偏差,这可能是数学建模时忽略了磁通泄漏、磁滞等因素的影响。为验证这些猜测的正确性,后续将针对插装式二维阀展开更多研究。
(4)试验结果验证了仿真的正确性,并且证明插装式二维阀的动态特性不弱于 MOOG D662-P伺服阀。
