机械装备的数字孪生结构参数分析与评价方法研究

康献民，陈尧，王建生，余宏志，谢奕浩，李宏宇，张迅

(五邑大学智能制造学部，广东江门 529020)

0 前言

数字孪生以数字化方式拷贝物理对象，模拟物理对象在现实环境中的行为，对物理对象设计、制造过程乃至整个工厂进行虚拟仿真。随着互联网与物联网的高速发展，在如今万物互联的时代，以数字孪生技术为基础的设计模式的优势性尤为突出。同时为达到数字孪生中物理实体与数字实体之间的互动，也需要经历诸多的过程和以大量基础支撑技术为依托，更需要经历很多阶段的演进才能很好地实现物理实体在数字世界中的塑造。首先要构建物理实体在数字世界中对应的实体模型，利用知识机制、数字化等技术构建一个数字模型，结合行业特性对构建的数字模型作出评分，判断产品制造的可行性。此外，还需要利用物联网技术将真实世界中的物理实体元信息采集、传输、同步、增强之后得到行业中的通用数据；通过这些数据可以仿真分析得到数字世界中的虚拟模型，在此基础上可以利用 AR/VR/MRGIS等技术，将物理对象外部特征在虚拟世界中完整复现出来，实现物理世界与信息世界的交融。在此基础上可以进一步地结合人工智能、大数据、云计算等各学科实现数字孪生模型的诊断、预警/预测及智能决策等共性应用,实现数字孪生在各个领域的应用与解决方案。

以数字孪生技术为基础研究机械装备的数字孪生模型设计方法，从概念域、结构域和参数域3个设计阶段实现和验证数字孪生模型设计方法的可行性。在机械装备的概念域中，从分析企业的需求到求解概念设计方案再到方案评价的同时进行优化分析评价。在机械装备的结构域中，对概念域得到的优化方案进行结构设计，按照机械设计准则，选择合适的结构评价指标,对结构进行优化评价。在机械装备的参数域中，对选择的机械结构进行细化;同时建立评价机械装备的标准以及相应的评价指标，采用BP神经网络方法评价优化迭代的过程。

本文作者在已经完成概念设计和结构设计的前提下，主要研究机械装备的数字孪生模型的参数设计。根据结构设计阶段设计的机械装备具体整机结构，在参数域设计时运用ANSYS Workbench软件对机械装备的整机结构进行静刚度分析，求解出可评价的数字孪生参数域的参数数据，如总变形、等效应力、等效应变；对整机结构进行动态特性分析，如模态分析(Model Analysis);根据分析的内容以及仿真结果，建立参数域评价模型标准以及指标体系，以专家知识为输入，建立BP神经网络模型,对选择的机械装备数字孪生模型的结构参数进行评价。

1 机械装备数字孪生结构参数分析

1.1 有限元分析步骤

本文作者主要使用ANSYS中的前处理、求解、后处理功能。机械装备有限元仿真分析流程如图1所示，图2所示为简化后的机械装备三维模型。

图1 机械装备有限元仿真分析流程

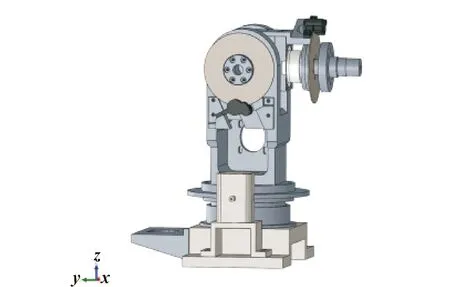
图2 简化后的机械装备三维模型

1.2 静刚度分析

静刚度分析是校核材料刚度和强度的一种有效方法，其方程如式(1)所示：

=

(1)

式中：为位移矢量；为刚度矩阵;为静力载荷。

在分析中应该满足假设条件：必须是连续的，材料需满足线弹性材料和小变形理论；不考虑随时间变化的载荷，也不考虑惯性(如质量、阻尼等)的影响。

运用ANSYS Workbench软件对机械装备的关键零部件和整机结构分别进行静刚度分析，是简单有效的分析方法，可分析结构在给定静力载荷作用下的响应。一般情况下，研究结构的位移、约束反力、应力以及应变等参数。

对机械装备同一工作姿态的夹具末端分别施加、、轴方向的载荷，载荷类型为Force，载荷分别为104.8、104.8、-52.4 N。对机械装备的底座添加固定约束Fixed Support。

使用Mechanical APDL solver进行求解，然后在求解结果中添加总变形、等效应变和等效应力这3项分析结果并显示。

总变形是一个标量，它由、、3个方向的变形量合成，计算公式如下：

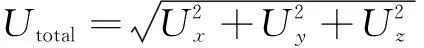
(2)

等效应变的计算公式为

(3)

等效应力通过描述一种结果在模型中的变化来快速、准确地表现出模型的最危险区域，等效应力的求解与主应力有关，公式如下：

=

(4)

某一姿态的制动器工作时，机械装备3个方向的总变形结果如图3所示。可知：最大整体变形发生在机械装备第3轴的夹具末端，、、轴载荷方向的最大变形分别为0.016 4、0.003 3、0.006 9 mm。

图3 制动器工作时的总变形云图

制动器工作时，机械装备3个方向的等效应力如图4所示。可知：等效应力最大值均出现在第三轴的夹具与第三轴制动盘固定法兰的接触位置，、、轴载荷方向的最大等效应力分别为5.627 8、1.456、2.647 2 MPa。

图4 制动器工作时的等效应力

制动器工作时，机械装备3个方向的等效应变如图5所示。可知：等效应变最大值均出现在第三轴的夹具与第三轴制动盘固定法兰的接触位置，、、轴载荷方向的最大等效应变分别为8.132 7×10、2.066 5×10、3.219 7×10mm/mm。

图5 制动器工作时的等效应变

1.3 动态特性分析

根据机械振动学理论，动力学通用方程如式(5)所示：

″+′+=()

(5)

式中：为质量矩阵；为阻尼矩阵；为刚度矩阵；″为加速度矢量；′为速度矢量；为位移矢量；()为力矢量。

当分析对象为无阻尼自由振动时，通常忽略阻尼矩阵，()=0，则式(5)可表示为式(6)：

″+=0

(6)

当物体的振动规律为简谐振动时，其振动的位移函数形式可以写成如式(7)所示：

=sin(+)

(7)

将式(7)代入式(6)得：

(8)

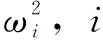
(9)

文中将静刚度分析所用到的简化模型、网格划分以及材料属性运用到模态分析，不需要添加载荷。

在制动器处于工作状态的前提下，根据各阶振型云图和固有频率验证该结构方案是否满足前期设计需求，更新计算结果。机械装备的前6阶模态频率以及相应的振型结果如图6所示。

图6 机械装备工作时的前6阶模态变形云图

机械装备整体结构的前6阶频率和振型如表1所示。

表1 机械装备的前6阶频率和振型

2 参数域评价指标构建

2.1 参数域评价标准的建立

机械装备参数域的评价模型应该包含机械装备相关参数的确定以及仿真等过程。同时借鉴能力成熟度模型集成技术中的目标，分级建立机械装备的数字孪生评价标准。综合考虑机械装备的强度、刚度、寿命、动态特性等多方面进行等级划分，根据机械装备参数域设计过程，将机械装备参数域评价等级划分为5个等级，实现机械装备参数域的可持续改进的层次划分，确定机械装备参数域智能化评定和发展的标尺。参数域评价标准如图7所示。

图7 参数域评价标准

级别1是原始级，表示机械装备的参数域指标中有1～2项满足基本要求，不能使用。级别2是初始级，表示机械装备的参数域指标中有2～3项满足基本要求，不能使用。级别3是使用级，表示机械装备的参数域指标中全部满足基本要求，可以使用。级别4是成熟级，表示机械装备的参数域指标中全部满足基本要求，并有1～2项满足优化要求，已经达到成熟级别，可以使用。级别5是优化级，表示机械装备的参数域指标中全部满足基本要求，并有3～4项满足优化要求，已经达到优秀级别，可以使用。

2.2 参数域指标体系的确定

由第2.1节机械装备相关参数可知，机械装备参数域的评价模型是一个复杂的系统，可以从不同的侧面反映机械装备的特性。根据层次关系，分析推导影响机械装备参数域特性的因素，得到整个机械装备参数域的指标体系。模型的目标层为机械装备参数域的评价；准则层包含强度、刚度、寿命、动态特性等指标；二级指标层包含一级准则层各元素的评价指标。机械装备参数域的评价模型体系如图8所示。

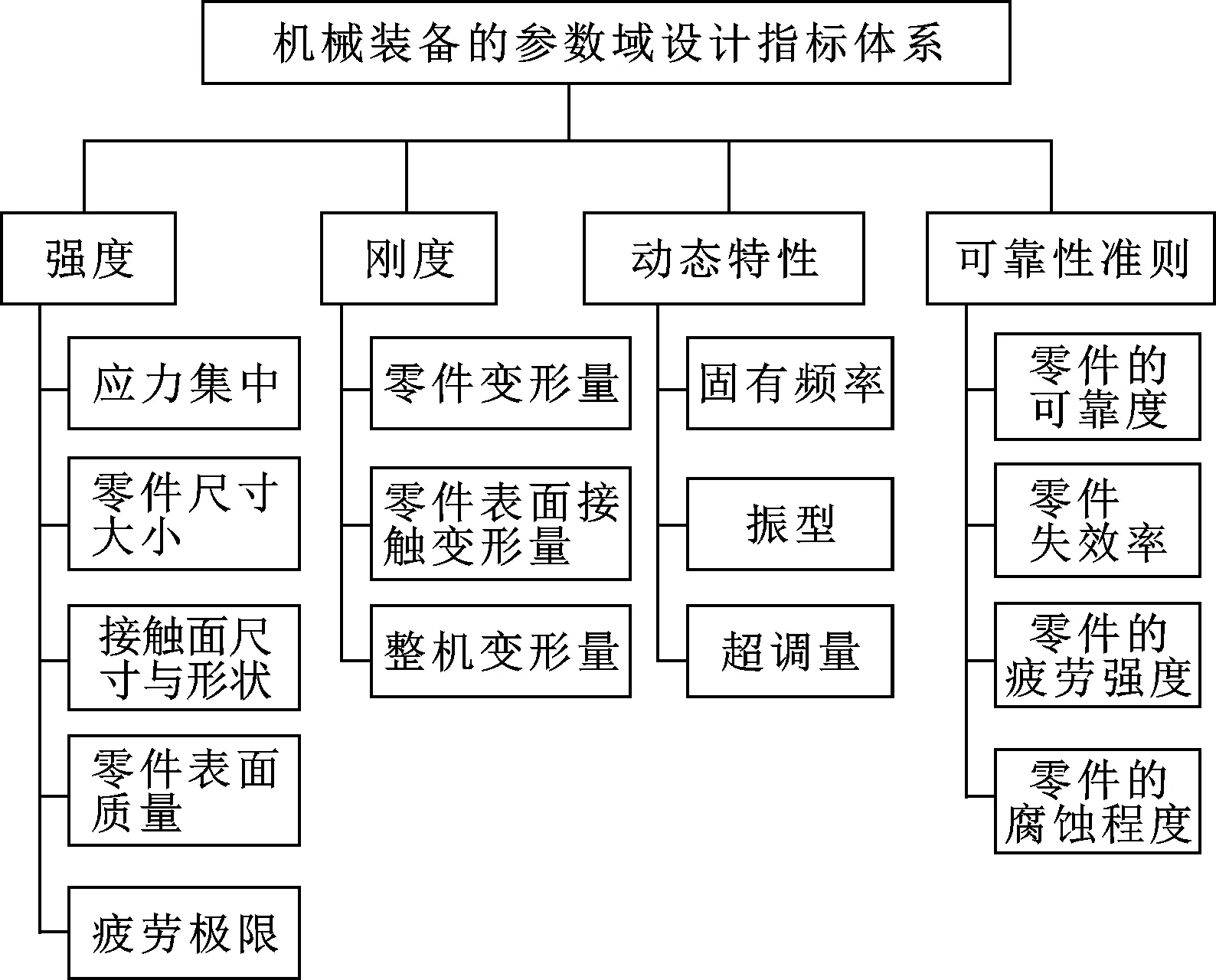
图8 机械装备参数域设计方案

3 机械装备参数域评价模型的构建

3.1 BP神经网络参数域评价模型

BP神经网络参数域评价模型分为3个层次，分别是输入层、隐藏层和输出层，每个网络层都包含有多个神经元，每个神经元都会跟相邻的前一层的神经元有连接，这些连接也是该神经元的输入。图9所示为BP神经网络参数域评价模型。

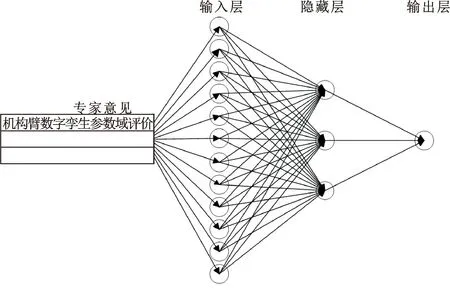
图9 BP神经网络参数域评价模型

3.2 参数域方案评价与迭代

由第1.2节可以得到机械装备结构的参数域设计方案，最大变形为0.016 4 mm，最大等效应力为5.627 8 MPa，最大等效应变为8.132 7×10mm/mm。

(1)机械装备底座静力学分析

机械装备的底座采用45钢。根据静刚度仿真得到：底座的最大变形为2.650 2×10mm，发生在与第一轴谐波减速器固定的位置；底座承受的最大等效应力为0.384 2 MPa，发生在底座凸台处；底座的最大等效应变为1.921 1×10mm/mm。机械装备的底座采用45钢，屈服极限强度为355 MPa，完全符合强度要求。

(2)机械装备第二轴外壳静力学分析

机械装备的第二轴外壳采用6061铝合金。根据静刚度仿真得到：第二轴外壳最大的变形为2.931 8×10mm，发生在顶端与第二轴制动盘连接的一侧；外壳承受的最大等效应力为0.108 9 MPa，发生在安装电机口处；外壳的最大等效应变为1.590 2×10mm/mm。第二轴外壳采用6061铝合金，屈服极限强度为55.2 MPa，完全符合强度要求。

(3)机械装备末端连接轴静力学分析

机械装备的末端连接轴采用6061铝合金。根据静刚度仿真得到：末端连接轴最大的变形为2.120 9×10mm，发生末端载荷作用处；末端连接轴承受的最大等效应力为2.583 5 MPa，发生在最上端的一个螺栓接触；末端连接轴的最大等效应变为6.136 1×10mm/mm。末端连接轴采用6061铝合金材料，屈服极限强度为55.2 MPa，完全符合强度要求。

(4)机械装备动态特性分析

在制动器处于工作状态的前提下，根据各阶振型云图和固有频率验证该结构方案是否满足前期设计需求，更新计算结果，机械装备在工作姿态1下的前6阶模态频率以及相应的振型结果。

对上述方案的实验条件和仿真结果进行BP神经网络分析。先邀请专家组以参数域评价指标为条件，对机械装备数字孪生参数域的的实验条件和仿真结果进行评价，再利用原有训练出来的BP神经网络专家库进行权重求和，结果如图10所示。可以看出：训练过程中的专家对机械装备参数域的指标评价的真实值与预测值之间的误差不大，说明训练得到的权重具有专家水平，可以进行反复测试评价。

图10 训练过程真实值与预测值的拟合结果

由图11可知：在测试过程中，专家组对机械装备参数域指标的评价的总误差不超过3.5%，说明测试得到的评价具有良好的参考价值。专家组的平均分为77.03，对照参数域评价标准图7，参数域方案属于成熟级别，则说明机械装备数字孪生模型的设计方案可以用来制造机械装备的物理样机。

图11 测试过程的误差分析

4 结论

本文作者在数字孪生参数域设计时运用ANSYS Workbench软件对机械装备的整机结构进行静刚度分析，求解出对数字孪生参数域评价有用的参数数据，如总变形、等效应力、等效应变；对整机结构进行动态特性分析，得到了机械装备在此工作姿态下的前6阶模态频率和相应的振型。

根据机械装备数字孪生结构参数分析得到的数字参数，提出基于专家知识的神经网络算法，以专家对于构建的机械装备参数域指标知识经验，作为神经网络的输入层，进行神经网络计算。根据构建的参数域评价指标体系，采用专家知识的神经网络算法对机械装备数字孪生模型的结构参数设计进行了评价，专家组的平均分为77.03，对照参数域评价标准属于成熟级别，说明机械装备数字孪生模型的设计方案可以用来制造机械装备的物理样机，验证了机械装备数字孪生模型结构参数设计的正确性与可行性。