浅埋偏压隧道边坡稳定性分析

2022-10-24蔡元成李吉刚赖金星

河北工程大学学报(自然科学版) 2022年3期

蔡元成，王强，张强，李吉刚，赖金星*

(1.长安大学公路学院，陕西西安 710064； 2.中铁建云南投资有限公司，云南昆明 650216)

近年来，我国公路交通行业蓬勃发展，重心逐渐由城市转移至山区。修建大量山区公路的同时，由于边坡周围岩土层较为软弱、强度低、极易滑动，稍有不慎就会导致围岩变形量骤然增大产生土体滑塌等事故，造成较大经济损失[1-2]。为防止该类灾害的发生，需将公路边坡土体开挖，但在边坡开挖过程中，如何保证其稳定性是工程界亟待解决的热点话题[3-4]。

目前，国内许多学者对隧道边坡开挖的支护措施开展了大量的研究，成果颇丰。邵珠山等[5]从边坡坡角、隧道开挖位置的角度出发分析其对边坡稳定性的影响，得到边坡及时支护后能够显著改善边坡的稳定性。贺思悦等[6]采用弧长法计算得到边坡稳定安全系数，对边坡进行桩锚联合支护后，边坡的剪应变与位移显著减小，验证了桩锚联合支护控制边坡稳定性效果显著。郑明新等[7]提出了三种边坡加固方案，结合现场实测对比发现，局部坡体钢花管注浆加固比坡体注浆防护的效果更好。吕敬富等[8]等人选用抗滑桩与桩板墙联合加固，使得隧道在开挖过程中处于稳定状态，最后对两种工况下既有铁道的水平位移进行分析，发现加固后水平位移约减少69%。王晓芳等[9]基于有限元软件并结合降强法探讨了边坡失稳判据，对抗滑桩强度、位置和长度对边坡的稳定性进行了分析，研究发现桩的埋置深度过大可能会导致桩体破坏。杨洪福[10]利用有限元软件控制放坡角度和锚杆长度进行参数优化得到最优参数，从而提出边坡的最佳处治方案。赵晓彦等[11]考虑了锚索与抗滑桩联合加固之间协调受力因素，结合工程实例探讨联合加固的优化设计方法，得到锚索预应力标准设计值与合理的抗滑桩设计方案。综上所述，国内学者对边坡的防治措施主要集中在单一锚杆或单一抗滑桩、喷射混凝土等方面，可对于围岩等级较高，地质条件恶劣的边坡，单一支护的加固效果并不理想，因此探究一种符合边坡变形特点的新型联合支护形式具有重要意义。

本文以某隧道边坡拟扩建公路工程为背景，提出“锚杆+抗滑桩”的联合支护方案，利用有限元软件探讨了联合支护参数对边坡稳定安全系数以及最大剪应变的影响，通过参数优化获得最佳支护方案。结合现场实测，对比分析了该支护方案下边坡及既有隧道的围岩变形特征，以期为同类工程提供一定参考价值。

1 工程概况

该隧道设计为双洞三车道对向行驶，沿东西向全长贯通，左线隧道里程桩号为ZK350+695—ZK353+625，长度为2 930 m；右线隧道里程桩号为YK350+715—YK353+638，长度为2 923 m。地表倾角为22°～45°，埋深较浅。洞底段隧道的中风化泥岩中节理裂隙呈微张状，发育较为严重，洞身段强风化泥岩围岩稳定性较差，属于Ⅳ级围岩。故综合判断隧道围岩为Ⅴ级，隧道出露段由土层全覆盖，边坡安全等级为一级。

经地质勘查可知，拟扩建公路隧道边坡一旦施工开挖后，在隧道拱顶处将会形成临空面，边坡产生滑塌的风险增大，对边坡的整体稳定性影响较大，如图1所示。

2 数值模拟

2.1 强度折减法

强度折减法[12]是指通过对土体强度参数经过一系列不断折减，最终迫使其达到失稳破坏临界状态的一个过程。通过该方法我们可以研究边坡的破坏情况、失稳过程等。因此它可以应用于边坡安全系数计算，针对Mohr-Coulomb破坏准则，安全系数F表达式为

图1 依托工程地理位置Fig.1 Geographical location of the relying project

(1)

(2)

式(1)、(2)中：ctrial为折减后的黏聚力，kPa；Ftrial为折减系数；c为黏聚力，kPa；φtrial为折减后的内摩擦角；φ为土体摩擦角。

2.2 模型建立

根据有限元软件建立隧道边坡开挖的三维弹塑性模型，岩土体采用Mohr-Coulomb本构模型，隧道双洞间距30 m，初期支护厚度为25 cm，二次衬砌厚度为50 cm，作安全储备考虑；整个模型长×宽×高=149 m×25 m×64.3 m，边坡仰角为45°。为探究锚杆+抗滑桩联合加固的效果，将三维模型划分为50 983个节点，65 106个单元，边坡模型中每个开挖面设置两排锚杆，锚杆选用直径为25 mm的HRB335钢筋，水平间距2.5 m，以植入式桁架梁单元模拟；同时设置截面尺寸2 m×3 m的抗滑桩，共5根，以实体单元进行模拟，如图2所示。模型计算的边界条件设置为四周固定边界，上表面取自然地表。

图2 计算模型Fig.2 Computational model

边坡开挖方案设定为分级开挖，共5级，在既有隧道选取2个典型断面进行监测，如图3所示。

图3 开挖监测断面示意图Fig.3 Schematic diagram of excavation monitoring section

2.3 材料物理力学参数

查阅山岭隧道相关设计规范，结合室内模型试验，得到围岩及支护结构模型参数如表1所示。

表1 围岩支护结构材料参数

3 参数优化

查阅相关路基设计规范，安全等级为一级的永久边坡安全稳定系数取1.35。故选取锚杆长度为8～16 m，每隔2 m设置一种工况，共五种工况；抗滑桩长度为10～20 m，每隔2 m设置一种工况，共6种工况，故与锚杆工况共5×6=30种工况，如表2所示。

表2 各工况下的边坡安全稳定系数

由表2和图4可知，当锚杆长度一定时，随着抗滑桩埋深增加，边坡的安全系数呈现不同程度的增长趋势。其中当锚杆长度在8～12 m范围之内变化时，抗滑桩的长度从10 m增长至16 m时，稳定安全系数基本呈现线性增长。当抗滑桩长度达到16～20 m之间时，锚杆长度在14～16 m之间时，安全系数略有增长，但增长幅度较小。如锚杆长度为14 m时，此时的抗滑桩从16 m增长为18 m时，安全系数仅增加0.004。

图4 安全系数与锚杆长度和抗滑桩长度关系Fig.4 Relationship between safety factor, anchor rod length and anti-slide pile length

当抗滑桩埋置深度一定时，增加锚杆的锚固长度时，边坡的安全系数在8～14 m之间呈现大幅度的增长，在14～16 m之间增长幅度较小，几乎保持不变。由此可知锚杆的长度达到一定程度时，稳定安全系数的增长逐渐趋于平缓状态。

边坡的稳定安全系数越高表示边坡整体越稳定，但是边坡的稳定还涉及到成本等多个因素[13]。由上述分析可知，过长的抗滑桩和锚杆的工况虽符合边坡稳定性要求，但继续增大对边坡的稳定安全系数影响较小，反而对成本的影响较大，故不予考虑。对于本边坡而言，当安全系数大于1.35时，即可认为该边坡安全[14]。

考虑一定安全储备的情况下，选取表2中安全系数为1.376～1.386之间的六种工况进行参数优化。由于抗滑桩相较于锚杆成本较大[15]，满足安全条件下，同样的锚杆长度下选取的抗滑桩长度越短越好，同样的的抗滑桩长度下锚杆越短越好，故可得以下三种方案：方案A：(抗滑桩14 m、锚杆14 m)；方案B：(抗滑桩12 m、锚杆16 m)；方案C：(抗滑桩16 m、锚杆10 m)。

选取方案A—C对其边坡土体内部最大剪应变规律[16-17]进行分析。方案A、B、C的最大剪应变如图5所示，经过对比三个方案的剪应变分布规律，最大剪应变均分布于上覆土与强风化泥岩的交界处并形成“U”形区，方案A的最大剪应变值为0.008 65；方案B的最大剪应变值为0.009 2；方案C的最大剪应变值为0.009；与方案B、C相比较，显然方案A的支护效果较好，边坡更加趋于稳定，为最佳方案。

4 结果分析

通过强度折减法计算得到边坡开挖后处于不支护工况下的安全系数为1.31，此时边坡处于不稳定状态。基于上述参数优化后选出的最佳方案A对边坡开挖后进行支护，对联合加固效果进行分析。

4.1 开挖对边坡位移的影响

边坡开挖后未加固工况下总位移、X方向位移、Z方向位移云图如图6所示。由图可知，土体在自重作用下产生的总位移为147.09 mm，X方向位移为55.07 mm，Z方向位移为140.48 mm。此时上部土层位移较大，破坏趋势较为明显。为进一步清楚地了解到模型的变形情况，截取模型土体滑动区中心处局部变形情况，如图7所示。可以看出，当模型失稳破坏时，上覆土体先滑动，后带动坡脚处土层滑动，从而造成坡体整体失稳。

图5 最大剪应变云图Fig.5 Maximum shear strain cloud chart

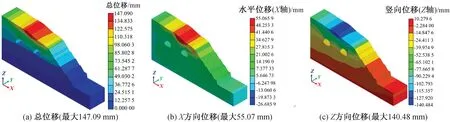
图6 未加固状态下位移云图Fig.6 Displacement cloud chart without reinforcement

图7 未加固变形区局部示意图Fig.7 Local schematic diagram of unreinforced deformation area

图8为边坡开挖后及时加固工况下总位移、X方向位移、Z方向位移云图。由图可知，土体在自重作用下产生的总位移变形为31.17 mm，X方向位移为23.41 mm，Z方向位移为4.50 mm。此时上部土体位移显著减小，土体处于稳定状态。为进一步清楚地了解到模型的变形情况，截取模型土体滑动区中心处局部变形情况，如图9所示。从中可以看出，上部土体变形区显著减小，有向坡脚转移的趋势。但经降强法折减计算此时边坡的安全系数为1.382，因此边坡不会失稳破坏。

4.2 抗滑桩应力与敏感性分析

抗滑桩应力分布图如图10所示，从图中可以看出，抗滑桩整体承受的应力分布情况大致相同，均为压应力，处于中风化泥岩的桩受到的压应力最大值位于抗滑桩中部，压应力最小值位于抗滑桩中上部，分别为0.21、0.07 MPa。桩体压应力形成了从桩体中端向上下两端依次减小的分布模式，每根桩的最大压应力都集中在0.17 MPa左右。

研究表明，抗滑桩桩位、桩距、桩长等因素均会对边坡稳定性有一定的影响[18-19]。分别设置桩长为10、12、14、16、18、20 m的抗滑桩来探究桩长的改变对桩身应力和其顶部水平位移的影响，如表3和图11所示。随着桩体埋深的增大，桩所受的最大压应力与桩顶水平位移逐渐减小，当埋深达到14 m时，最大应力下降至最小值约为0.24 MPa，桩顶位移下降至2.63 mm。当桩体埋深继续增大时，最大应力下降幅度较小，位移减少幅度不显著，对边坡稳定性影响较小，故认为抗滑桩长度为14 m最为合适。

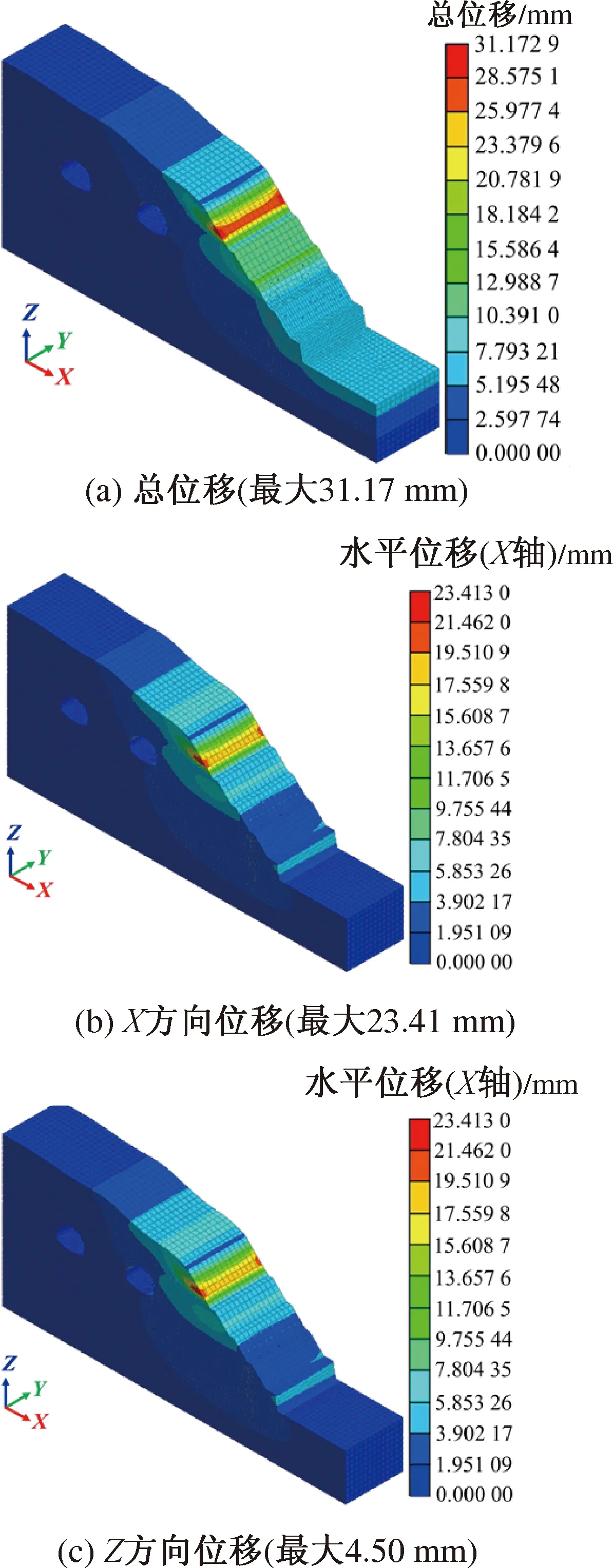
图8 加固状态下位移云图Fig.8 Displacement cloud chart under reinforcement

图9 加固后变形区局部示意图Fig.9 Local schematic diagram of deformation area after reinforcement

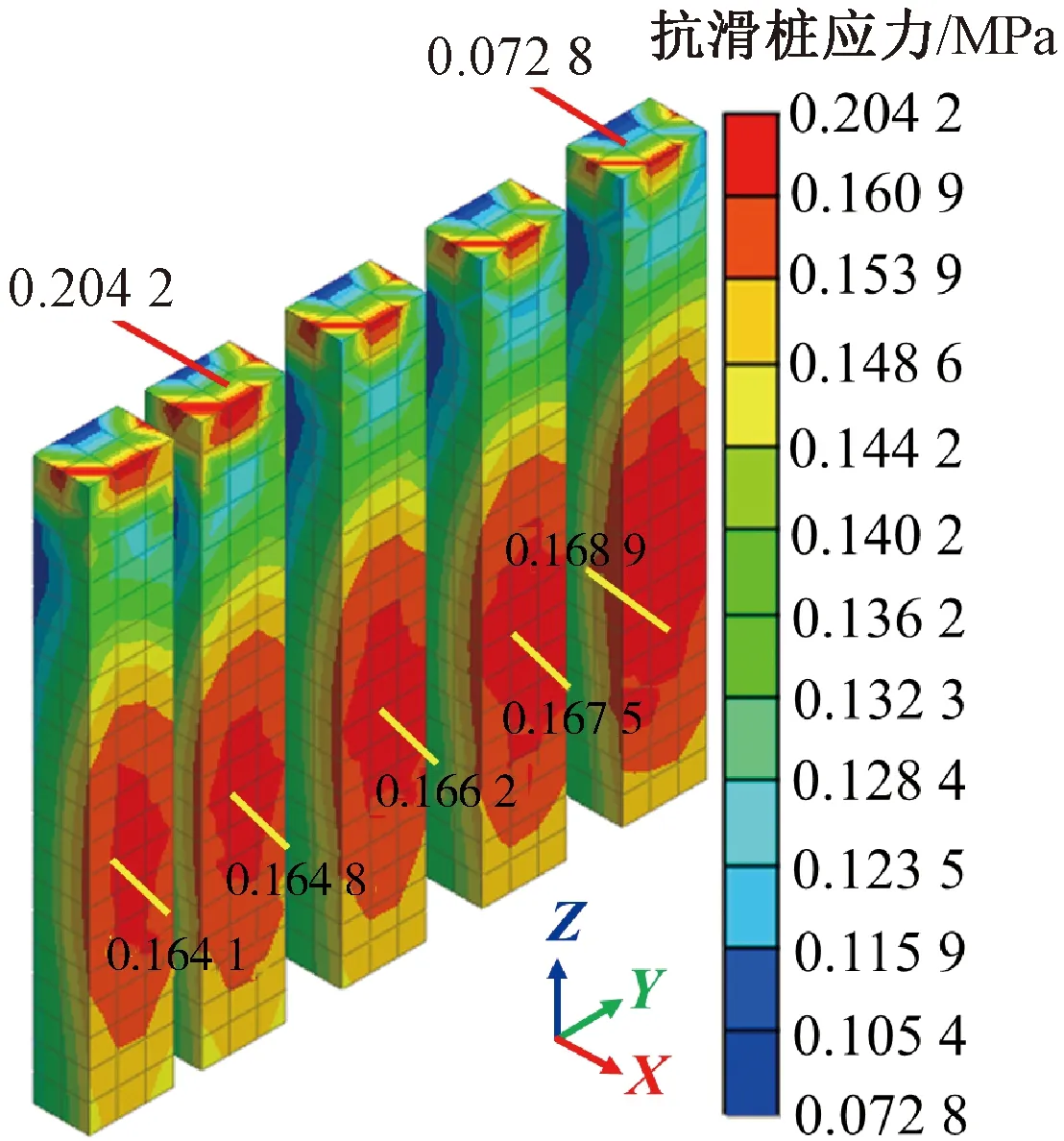
图10 抗滑桩Mises应力分布图Fig.10 Mises stress distribution of anti-slide pile

表3 不同桩长下最大应力值及桩顶位移统计

4.3 锚杆轴力分析

锚杆支护的目的就是为了更好地减少坡体上部的剪应力集中现象，使得土体内力分布更为均匀。通过改变锚固长度来探讨对锚杆轴力影响规律，如表4所示。

表4 不同锚固长度下最大轴力值统计

由表4可以得到，随着锚杆锚固长度的增加，最大轴力值呈现线性减少趋势，当锚固长度到达14 m时，最大轴力值下降至128.84 kN。当继续增大锚固长度时，最大轴力值下降幅度较小。故认为锚杆长度为14 m最佳。

5 开挖对既有隧道的影响

5.1 测点布置

为扩建公路，边坡分级开挖的过程中，随着开挖深度的增大，边坡卸荷导致应力重分布，势必对隧道产生一定的影响，选用全站仪对隧道左线两个断面拱顶进行沉降观测，测线1与测线2处布置数显收敛仪来监测隧道的水平收敛情况，如图12所示。

图11 不同桩长的抗滑桩应力分布图Fig.11 Stress distribution diagram of anti-slide pile with different pile lengths

图12 断面测点位置Fig.12 Location of observation points of sections

隧道ZK352+500—ZK352+700段左侧有一水库，该段节理裂隙较发育，穿越地质薄弱带，施工不当或支护不及时存在坍塌、掉块风险。故本文选取ZK352+557、ZK352+568两个典型断面来监测并记录整个施工过程中拱顶沉降与测线1、2的水平收敛情况，以此来反映边坡开挖深度对既有隧道变形的影响规律。

5.2 监测数据分析

对ZK352+557断面、ZK352+568断面的拱顶累积下沉、下沉速率、累计水平收敛及水平收敛速率进行了监测分析，如图13、图14所示。

从图13分析可知，ZK352+557断面的拱顶累计下沉量随着边坡开挖深度的增加，前期呈现线性增长的趋势；但当开挖到20 m时，拱顶的下沉速率逐渐降低，下沉量缓慢增加，最大累计下沉量为32.24 mm，下沉速率最大为2.27 mm/d。测线1与测线2的水平收敛速率在开挖0～10 m范围内较大，最高达4.32 mm/d，水平累计收敛急剧增大，但测线2的收敛速率略低于测线1，两者累计水平收敛随着开挖深度的增加总体上仍呈现增长趋势。

同理对ZK352+568断面进行分析，如图14所示。与ZK352+557断面相比，两者的累计拱顶沉降增长趋势在0～20 m几乎一致；随着开挖深度继续增大时，ZK352+568断面下沉量几乎保持不变，下沉速率略小于ZK352+557断面。ZK352+568断面的水平收敛速率在0～10 m相对较大，最大值增至1.72 mm/d，与前述断面不同的是，曲线整体上呈现大幅度波动降低的趋势，且测线2的收敛速率略大于测线1的收敛速率。